Circuits and Systems, 2011, 2, 112-120
doi:10.4236/cs.2011.23017 Published Online July 2011 (http://www.SciRP.org/journal/cs)
A Fluctuation-Dissipation Model for Electrical Noise*
Jose-Ignacio Izpura, Javier Malo
Group of Microsystems and Electronic Materials, Universidad Politécnica de Madrid, Madrid, Spain
Received February 5, 2011; revised April 6, 2011; accepted April 13, 2011
Abstract
This paper shows that today’s modelling of electrical noise as coming from noisy resistances is a non sense
one contradicting their nature as systems bearing an electrical noise. We present a new model for electrical
noise that including Johnson and Nyquist work also agrees with the Quantum Mechanical description of
noisy systems done by Callen and Welton, where electrical energy fluctuates and is dissipated with time. By
the two currents the Admittance function links in frequency domain with their common voltage, this new
model shows the connection Cause-Effect that exists between Fluctuation and Dissipation of energy in time
domain. In spite of its radical departure from today’s belief on electrical noise in resistors, this Complex
model for electrical noise is obtained from Nyquist result by basic concepts of Circuit Theory and Thermo-
dynamics that also apply to capacitors and inductors.
Keywords: Admittance-Based, Noise Model, Fluctuation, Susceptance, Dissipation, Resistance
1. Introduction
Current understanding of electrical noise in circuits con-
siders shot and Johnson noises as different physical phe-
nomena each with its own physical model, despite their
deep connection found by some authors [1]. Considering
electric current as carried by discrete electrons inde-
pendently of one another, as Johnson did in vacuum de-
vices to study their shot noise [2], this connection isn’t
too surprising. What is a surprise, however, is that to-
day’s works in this field tend to consider noise currents
as carried by packets of electrons that, to our knowledge,
hardly are found in ordinary matter. We mean proposals
like [3] contending that electrical charge piling-up in a
lonely resistance R generates shot noise, thus transgress-
ing a Quantum-Mechanical result of [4]: the need for a
Complex Admittance function to describe a noisy system.
This transgression and that of Special Relativity that a
null C shunting the R of a resistor endures [5], led us to
review today’s modelling of electrical noise in this paper
showing why the PSPICE simulator does not give the
right noise of junction diodes [6] and what the effects are
of today’s unawareness about the Susceptance that
shunts the Conductance G = 1/R of any resistor we can
make. The paper is organized as follows. In Section 2 we
review the Partial Interpretation (PI) in use today of
Johnson-Nyquist results that leads to a wrong modelling
of electrical noise sometimes. Section 3 shows how to
pass from this PI to an Advanced Model (AM) for elec-
trical noise that agreeing with the laws of Physics, also
allows a right modelling of this noise where the aforesaid
PI fails. This passage is done in frequency domain by the
familiar noise densities


I
Sf in 2 AHz and


V
Sf in
2
VHz. Section 4, however, considers the generation of
electrical noise by Fluctuations and Dissipations of elec-
trical energy in time domain, taking place in the Admit-
tance of two-terminal devices like resistors and capaci-
tors, no matter its physical structure. Some relevant con-
clusions are drawn at the end.
2. Reviewing Current Model for Electrical
Noise in Resistors
To a first level, the Susceptance shunting the conductance
1GR

of a resistor of resistance R is due to a capaci-
tance Cd coming from the dielectric properties of the
material used to fabricate this device, whose physical
structure appears in Figure 1 and where the space be-
tween two parallel plates (ohmic contacts) contains some
material of dielectric permittivity ε and conductivity σ.
We mean the Susceptance due to dd
CR

 that each
resistor bears in parallel with its R because the non-null
dielectric relaxation time d

  of its inner material
*Work supported by the Spanish CICYT under the MAT2010-18933
p
rojec
t
, by the Comunidad Autónoma de Madrid through its IV-PRICIT
Program, and by the European Regional Development Fund (FEDER).

J.-I. IZPURA ET AL.
113
[7]. Any stray capacitance as pF, typical of
set-ups used in Low Frequency Noise (LFN) measure-
ments [8], would be added to Cd.
0.5
stray
C
For conducting materials as n-doped Silicon or GaAs,

d falls below the ps, thus giving very low Cd values:
F for R = 1 k and 
d = 1 ps. This is why Cd
and Cstray are considered irrelevant at frequencies f ≤ 1
MHz where LFN is found. This irrelevance that can be
accepted numerically in most cases (e.g. when there are
other Admittances in parallel), leads to the misconcep-
tion underlying the aforesaid PI of the pioneering works
of Johnson [9] and Nyquist [10]. This error is so
deep-rooted in today’s research that reviewers of [3]
were not ashamed of publishing a piling-up of electrical
charge in a resistance devoid of capacitance C, which
links electric charge and electric voltage
15
10
d
C 

Qt


vt .
When a current


it produces a change of dipolar
charge as t passes, it builds a voltage Qit v

that is linked with the charge variation at each instant by
the Capacitance CQv . Thus, C = 0 between the
two terminals of a resistor means that it could show an
electrical voltage between them without electric charges
acting as its source or, as we wrote in [5], its material
having finite σ to offer a finite R with the structure of
Figure 1, but having a null permittivity ε = 0 to offer Cd
= 0, would allow an infinite speed for the electromag-
netic wave, thus infringing Einstein’s Special Relativity.
Besides this conflict with Physics, this PI of Nyquist
work is hard to apply out of Thermal Equilibrium (TE)
because [10] was done for TE. The footnote of Figure
4.11 of [11] summarizes the essence of this PI by this
sentence: “Circuits elements and their noise models.
Note that capacitors and inductors do not generate
noise”.
Figure 2 shows the circuits this PI uses to represent
electrical noise in a resistor of resistance R, where a
Conductance 1GR is shunted by a noise generator
of density

4
I
Sf kTR 2 AHz (Nyquist noise) for
k being the Boltzmann constant. This leads to a noise
density VI

2
Sf RSR

4f kT2 VHz (Johnson
noise). Thus, a resistor is a noisy resistance [3] for this PI
that uses the resistance R of a resistor in TE as a genera-
tor of flat and V noises up to frequencies
fQ  6.2 THz at room T, a quantum limit given in [10].

I
Sf S

f
Let’s consider under this PI the circuit of Figure 3
with C = 0, where the voltage of a resistor of R = 100 k
is sampled and feedback as a current by a feedback factor
β = 1/R A/V. For this R = 100 k giving


4
V
Sf kTR
1600

2
nVHz and


0. 16
I
Sf

2
p
A Hz

, the noise-
less sampling and feedback of Figure 3 could be carried
out quite well with today’s Operational Amplifiers [12]
having input noise parameters as: 2
236 nVHz
n
e
and

2
2
n
i1fAHz. Accordingly to the PI in use today
this negative feedback adds a noiseless R in parallel with
the noisy R or resistor whose Nyquist noise


I
Sf is
the input signal of this feedback circuit. Thus, the


I
Sf of the noisy R is the only source of noise in this
circuit that, attenuated by the noiseless R, leads to


kT
VFB
Sf R 2
VHz
in it. This result agreeing with
Figure 1. Physical structure of an elemental resistor whose
ohmic contacts (shaded area) are the plates that enclose the
parallel-plate capacitor of capacitance Cd = τd/R that allows
to apply or to measure an electrical voltage between the
terminals A and B of its resistance R.
Figure 2. Parallel and series circuits that today’s Partial
Interpretation (PI) of Johnson and Nyquist results uses to
represent the electrical noise of a resistor (see text).
(a)
(
b
)
Figure 3. Feedback scheme used to show that today’s un-
awareness about the role of Susceptance in electrical noise,
doesn’t allow finding the “we ll known” kTC noise of the
capacitor existing in this circuit.

114 J.-I. IZPURA ET AL.
a “well know” one of this PI, namely: “the available
noise power from a resistor of resistance R in TE at some
T is

Nf kTWHz”, deserves some attention.
Because the noisy R and the noiseless R are driven by

SfkTR
VFB
2
VHz, they are dissipating


Nf


VFB SfRkTWHz, of course. Since the noisy R
is out of TE due to its feedback, we find logical this
lower dissipation than the 4kT W/Hz it dissipated in TE
when it was driven by . What is less “logical” is
the null dissipation R has in the equivalent circuit of
Figure 2 with series connected with R, thus rais-
ing doubts about the physical correctness of

I
Sf

f
V
S


V
Sf

, whose circuital correctness is well known.

2
I
RSf
To make some progress, let’s consider the noisy R
shunted by C = 1 pF in Figure 3 to represent a pixel of
an imaging device becoming charged by m electrons
when a short packet of m/η photons is absorbed with
quantum efficiency η < 1. “Short” means that photons
are absorbed within a time interval tRC

,
where τ is the time constant of this R-C cell. Thus, a
photon packet sets a charge of mq C in C (q is the elec-
tron charge) and the voltage vmqC

 V appearing
on R will be the aimed Signal on R whose power is: S =

2
mqCR W. Since C will discharge through R, the
Signal readout would be done a short time d
t


after the photon absorption in order to find the aforesaid
power S. Concerning Noise power N, the mean square
noise voltage on R is the product of the Johnson noise

4
V
Sf kTR V
2/Hz by the noise bandwidth N
BW



2C
f
of this circuit of cut-off frequency


12
C
f
RC
[13]: N = SV × BWN. This replaces the integration in f of
to allow a fast reasoning using Signal to Noise
ratios (

V
Sf
SN). Thus, the noise power in the pixel with-
out feedback is:

NkTRC W and its SN is:

i
SN 
 
2
mqkTC , the ratio of the square charge
signal in C C
2, divided by the square charge
noise of C: kTC C2 [14]. To give some figures, the kT/C
noise at room T (e.g. the square root of

2
mq
kT of C = 1
pF is 64 Vrms. For a Signal ∆v =
C)
mq 6.4 mV we
would have:
C =
4
i10 SN 40 dB for the pixel with-
out feedback.
or
With feedback, however, the BWN doubles due to
R2 shunting the same C that this feedback in-phase
with the output doesn’t vary [15]. From this double
BWN with the noise power on R is:
FB

VFB
SfkT

3. An Advanced Model for Electrical Noise
in Resistors and Capacitors
Because CQv

 links charge variations with volt-
age ones related with electric fields storing energy be-
tween terminals, C behaves as the reservoir of electrical
energy whose thermal Fluctuations are observed as
Johnson noise v(t) in resistors [7]. Using Thermodynam-
ics, C sets the Degree of Freedom to store electrical en-
ergy linked with the fluctuating v(t) in a resistor that a
lonely resistance doesn’t have. Using Quantum Mechan-
ics we will say that eingenstates of electrical energy
hardly will be found in a lonely resistance unable to store
it by some Susceptance in parallel or by a Reactance in
series. Thus, a cogent model for electrical noise in resis-
tors must handle Conductance 1GR together with
Susceptance, and this also holds for noise modelling of
capacitors in TE at some temperature T because they
offer a similar Admittance [5].
It is worth noting that these ideas about noise in resis-
tors are present in Figure 2 if one knows how to read its
first circuit or which is the physical meaning of



I
Sf

A2/Hz, a current-like power source proportional
to the conductance it is driving. This I leads to
4kTG

Sf


V
Sf 4kTR V
2/Hz, a power density that, being pro-
portional to R while its bandwidth (note that Cd always
exists) is proportional to 1/R, means that the mean
square voltage noise has nothing to do with currents in
R. Thus, the noise currents that

4Sf
I re-
presents must be currents inQ(t) orthogonal to noise
currents inP(t) in G that always are in-phase with the
voltage noise vn(t). This means currents inQ(t) always in
quadrature with vn(t) flowing through a Susceptance
shunting
kTR
1GR

. The compound device Nyquist used
in [10] agrees with this feature of the AM for electrical
noise we are going to show. This AM used to explain
the 1/f excess noise of Solid-State devices [7] and the
flicker noise of electron fluxes in vacuum ones [5],
never has been described before at this level of detail,
especially in time domain.
The Susceptance or ability to store electrical energy
our AM uses replacing the Transmission Line of [10], is
the circuit element providing a Degree of Freedom to
store electrical energy liable to fluctuate thermally in the
device. These Fluctuations giving rise to the Johnson
noise of resistors, don’t take place in R, but in its Sus-
ceptance that must be capacitive because the flat


4
V
Sf kTR V
2/Hz found by Johnson at low f [9] is
not possible for an inductive Susceptance with Fluctua-
tions of energy of finite power. To make easier the pas-
sage from the PI to our AM let’s consider the electrical
noise of a two-terminal circuit that can be reduced to a
capacitance C at high f. The equipartition value for one
R
N2RCkT W. Since the Signal power on R
doesn’t change because C doesn’t vary, the (SN) of
the pixel with feedback would be doubled, a result well
worth patenting provided it was true. Unfortunately,
this noise modelling is wrong as we will show in the
next Section.

J.-I. IZPURA ET AL.
115
Degree of Freedom applies to C in this case [14] and this
gives the mean square voltage noise of C in TE from this
equality:
 
22
11
22
kT
kTCv tv tC 
(1)
thus showing that the mean square voltage of noise has
nothing to do with currents in R as we concluded previ-
ously from Circuit Theory and why this is so.
Because (1) gives the kTC noise of capacitive de-
vices that doesn’t depend on the R that shunts C [13,14],
let us consider the noise of the BAT85 Schottky diode of
[6] whose PSPICE model appears in Appendix I. Due to
its CJ0 = 11.1 pF, the kTC noise of this diode at room
T is:

2
vt = 3.7  10–10 V2 or 19.3 Vrms. From its
saturation current Isat = 211.7 nA and the ideality factor n
= 1.016 of its i-v curve, CJ0 is shunted in TE by a resis-
tance

1
00v dTsat
riv nVI

  = 124.1 k, where
T
VkTq is the thermal voltage. Following our AM,
the room T noise density of this diode at low f must be:
V
2/Hz in TE because this is the value
giving

04
VAM d
S

kTr
2
vt = 0
J
kT C in CJ0 to fulfil (1). There-
fore, is this low-pass, Lorentzian spectrum:

VAM
Sf


0
2
0
00
1
42
21
121
d
VAM
J
dJ
c
kTr f
kT
Sf C
frC
c
f




(2)
that integrated from to gives 0ff


2
vt
= 0
J
kT C as it must be by Equipartition.
Using PSPICE we have obtained the i-v curve of this
diode shown in Figure 4 with a logarithmic axis to show
its exponential character. Besides the simulated i-v we
also present (by dots) the i-v solely due to thermoionic
current represented by this equation:
9
3
exp 1
211.7 10exp1
1.01625.8510












 
 



sat
T
v
iI nV
v

(3)
The superposition of the two curves shows that cur-
rents through R1 = 36 M used by PSPICE to get a better
fitting in reverse mode (see Appendix I), are negligible.
The inset of Figure 4 shows the i-v curve with linear axis
in the region (v  0) where a resistance R*(v = 0) = 123.7
k can be found. This R* is: R* =

010 1dd
rRrRr
0d
Vrms. This SVPI(0) being 24.6 dB below SVAM(0) = 4kTR*
.
Curve a) of Figure 5 is the PSPICE gives for
this diode in TE (i = 0 in the inset of Figure 5), whose
flat SVPI(0) = 171.5 dB at low f means 1.13 Vrms noise
in this diode whereas our AM states that it will be 19.3
= 146.9 dB, is a 292 times lower noise that PSPICE
gives because it considers (as the aforesaid PI) that the
only source of noise in the diode at v = 0 is R1 = 36 M,
whose Nyquist noise

V
Sf


1
4
I
Sf kTR drives the paral-
lel circuit of rd0, R1 ans a low-pass spec-
trum of amplitude SVPI (0) =

d CJ0. This give2
*
1
4kTRR V
2/Hz at
low f that is R1/R* times lower t0) = 4kTR*
that our AM states to keep the
han the SVAM(
0
J
kT C noise of 0
J
C
shunted by R*. Since 10

1
log .6RR dB, this
plains why today’s PI ofils to give a
well known
* 24
Nyquist result fa
ex-
kTC noise. Concerning circuit elements,
PSPICE conshem perfectly as it is shown by the
cut-off frequency fc =
ider t


*
0
12J RC = 115.6 kHz of
curve a in Figure 5.
Taking advantage of the correctness of the fc PSP
gi
ICE
ves, we have simulated this diode out of TE, under a
forward current i = Isat. The noise spectrum thus obtained
is curve b of Figure 5, whose fc = 222.4 kHz comes from
the low dynamical resistance of the diode under this
forward bias: rd (i = Isat) = rdfw = 62 k, and its similar
junction capacitance (slightly higher with the voltage v =
18.2 mV set by this i = Isat biasing the diode). Note that
while the diode capacitance varies slightly for such a
small voltage, the diode resistance varies as: exp(v/nVT)
BAT85 Figure 4. Current-voltage (i-v) characteristics of the
Schottky diode obtained by PSPICE (line) and its ther-
moionic values (dots) given by (3) (see text).
–
150
–
175
–
200
Figure 5. Noise densities SV(f) obtained by PSPICE for the
BAT85 Schottky diode at room T: a) without bias (Thermal
Equilibrium, i = 0) and b) under forward bias (i = Isat).
Curve a) does not give the kTC noise of its junction ca-
pacitance (see text).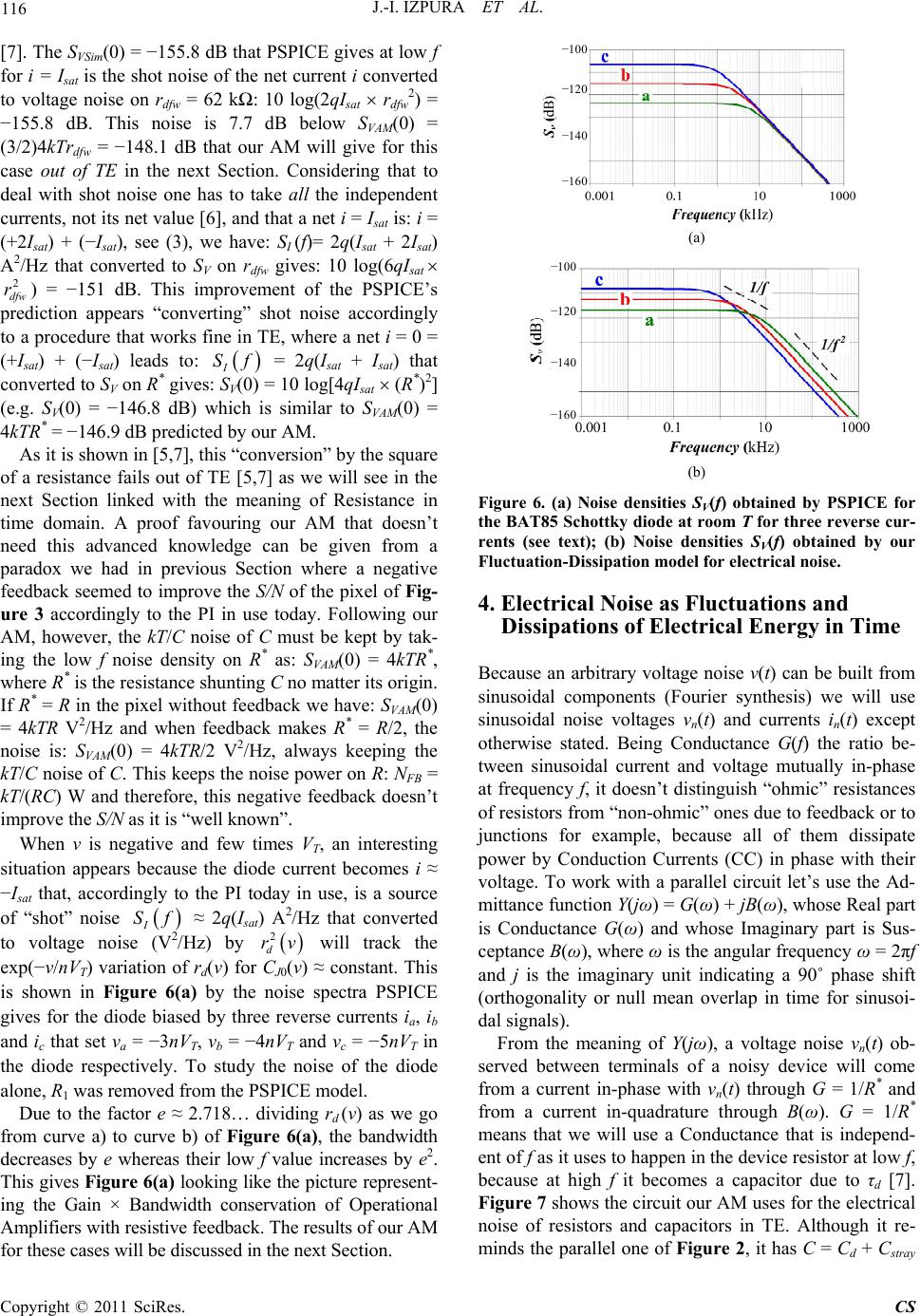

116
B tha
J.-I. IZPURA ET AL.
[7]. The SVSim(0) = 155.8 dt PSPICE gives at low f
for i = I is the sho
sat t noise of the net current i converted
to voltage noise on rdfw = 62 k: 10 log(2qIsat  rdfw
2) =
155.8 dB. This noise is 7.7 dB below SVAM(0) =
(3/2)4kTrdfw = 148.1 dB that our AM will give for this
case out of TE in the next Section. Considering that to
deal with shot noise one has to take all the independent
currents, not its net value [6], and that a net i = Isat is: i =
(+2Isat) + (Isat), see (3), we have: SI (f)= 2q(Isat + 2Isat)
A2/Hz that converted to SV on rdfw gives: 10 log(6qIsat 
2
dfw
r) = 151 dB. This improvement of the PSPICE’s
prediction appears “converting” shot noise accordingly
to a procedure that works fine in TE, where a net i = 0 =
(+Isat) + (Isat) leads to:


I
Sf = 2q(Isat + Isat) that
converted to SV on R* gives: SV(0) = 10 log[4qIsat  (R*)2]
(e.g. SV(0) = 146.8 dB) whih is similar to SVAM(0) =
4kTR* = 146.9 dB predicted by our AM.
As it is shown in [5,7], this “conversion” by the square
of a resistance fails out of TE [5,7] as we
c
0
will see in the
next Section linked with the meaning of Resistance in
time domain. A proof favouring our AM that doesn’t
need this advanced knowledge can be given from a
paradox we had in previous Section where a negative
feedback seemed to improve the S/N of the pixel of Fig-
ure 3 accordingly to the PI in use today. Following our
AM, however, the kT/C noise of C must be kept by tak-
ing the low f noise density on R* as: SVAM(0) = 4kTR*,
where R* is the resistance shunting C no matter its origin.
If R* = R in the pixel without feedback we have: SVAM(0)
= 4kTR V
2/Hz and when feedback makes R* = R/2, the
noise is: SVAM(0) = 4kTR/2 V2/Hz, always keeping the
kT/C noise of C. This keeps the noise power on R: NFB =
kT/(RC) W and therefore, this negative feedback doesn’t
improve the S/N as it is “well known”.
When v is negative and few times VT, an interesting
situation appears because the diode current becomes i 
Isat that, accordingly to the PI today in use, is a source
of “shot” noise

I
Sf  2q(Isat) A2/Hz that converted
to voltage noise (V2/Hz) by

2
d
rv will track the
exp(v/nVT) variation of rd(v) for CJ(v)  constant. This
is shown in Figure 6(a) by the noise spectra PSPICE
gives for the diode biased by three reverse currents ia, ib
and ic that set va = 3nVT, vb = 4nVT and vc = 5nVT in
the diode respectively. To study the noise of the diode
alone, R1 was removed from the PSPICE model.
Due to the factor e  2.718… dividing rd (v) as we go
from curve a) to curve b) of Figure 6(a), the bandwidth
decreases by e whereas their low f value increases by e2.
This gives Figure 6(a) looking like the picture represent-
ing the Gain × Bandwidth conservation of Operational
Amplifiers with resistive feedback. The results of our AM
for these cases will be discussed in the next Section.
100
120
140
160
(a)
100
120
140
160
(b)
Figure 6. (a) Noise densities S(f) obtained by PSPICE for
the BAT85 Schottky diode aom T for three reverse cur-
Dissipations of Electrical Energy in Time
Be
nusoidal components (Fourier synthesis) we will use
en terminals of a noisy device will come
fro
V
t ro
rents (see text); (b) Noise densities SV(f) obtained by our
Fluctuation-Dissipation model for electrical noise.
4. Electrical Noise as Fluctuations and
cause an arbitrary voltage noise v(t) can be built from
si
sinusoidal noise voltages vn(t) and currents in(t) except
otherwise stated. Being Conductance G(f) the ratio be-
tween sinusoidal current and voltage mutually in-phase
at frequency f, it doesn’t distinguish “ohmic” resistances
of resistors from “non-ohmic” ones due to feedback or to
junctions for example, because all of them dissipate
power by Conduction Currents (CC) in phase with their
voltage. To work with a parallel circuit let’s use the Ad-
mittance function Y(jω) = G(ω) + jB(ω), whose Real part
is Conductance G(ω) and whose Imaginary part is Sus-
ceptance B(ω), where ω is the angular frequency ω = 2f
and j is the imaginary unit indicating a 90˚ phase shift
(orthogonality or null mean overlap in time for sinusoi-
dal signals).
From the meaning of Y(jω), a voltage noise vn(t) ob-
served betwe
m a current in-phase with vn(t) through G = 1/R* and
from a current in-quadrature through B(ω). G = 1/R*
means that we will use a Conductance that is independ-
ent of f as it uses to happen in the device resistor at low f,
because at high f it becomes a capacitor due to τd [7].
Figure 7 shows the circuit our AM uses for the electrical
noise of resistors and capacitors in TE. Although it re-
minds the parallel one of Figure 2, it has C = Cd + Cstray

J.-I. IZPURA ET AL.
117
y: iQ(t) = jB  vn(t) that,
fo
shunting its R* that includes ohmic and non-ohmic resis-
tances defining the Conductance G = 1/R* of the Admit-
tance we will use to handle noise voltage v(t) as the sig-
nal linking noise current in its Conductance with noise
current in its Susceptance at each f. Being vn(t) a sinu-
soidal component of v(t), the noise current through G =
1/R* is the sinusoidal current in-phase with vn(t) given by:
iP(t) = G  vn(t) (see Figure 8 ).
The noise current iQ(t) of Figure 8 is a noise current
in-quadrature with vn(t) given b
r this positive B due to C, will be +90˚ phase-advanced
respect to vn(t). Hence, the time integral of iQ(t) and vn(t)
have the same Phase, thus suggesting what our AM con-
siders: that the Displacement Current (DC) at each f iQ(t)
is the Cause that, integrated in time by C, produces the
Effect vn(t) that synthesizes Johnson noise in resistors
and kT/C noise in capacitors. To study noise coming
from Fluctuations in time of electrical energy, let’s use
the instantaneous power function: p
i(t) = vn(t)  i n(t)
where in(t) = iP(t) + iQ(t) is the whole current in the de-
vice. To work in time domain, the noise density 4kT/R*
A2/Hz of Figure 7 is replaced by the random current iNy(t)
with zero mean shown in Figure 8, whose equation on
top (Kirchoff’s law) we will write as:
 
n
nN
vt
CGvti
t
 


y
t (4)
Equation (4) states that any real iNy(t) w
a DC in C and a CC in R*. To create only a DC, a -like
i
For a
e seen the need of C to
ha
ve use the term
en the ohmic contacts due to thermal ac-
tiv
eaction events
ta
ill create both
Ny(t) of infinite bandwidth (BW) or null duration
(0
c
t) is needed. For this -like iNy(t) having a
weight q in t (charge), the time inal of (4) during
cgives a step vbuilt = q/C V created instantane-
ously in C by the -like iNy(t).
n uncharged C (v = 0), a Fluctuation of q2/(2C) J
appears in C, whence it may b
tegr
0t
ve fluctuations of electrical energy in a resistor. Al-
though pure Fluctuations of energy won’t exist in resis-
tors because their iNy(t) is band-limited [10], there can be
fast DC with short c t looking like very pure Fluctua-
tions of energy in this circuit. They will include, however,
a small, non null Disation due to the CC existing dur-
ing the non null c t elapsed, whence it may be seen that
an electron leaving one plate with a kinetic energy of
q2/(2C) J exactly is unable to create vbuilt = q/C V in C
because part of its q2/(2C) energy is dissipated during its
transit time c t. For *
c tRC however, this passage
of one electron between plates of C is a very energy-
conserving ent beca Gvn(t) “has no time”
to dissipate a noticeable energy during this fast DC or
thermal jump of an electron of charge q between the oh-
mic contacts or plates of C. This fast DC would be a pure
Fluctuation of energy (e.g. devoid of Dissipation) given
the orthogonal character of these two phenomena (see
Appendix II).
Let’s call Thermal Action (TA) this fast transit of an
electron betwe
sip
ity. For a capacitor made from two metal plates in
vacuum, thermoionic emission would produce directly
these TA [5], whereas for resistors with conducting ma-
terial between plates, TA would appear in the way pro-
posed in Appendix III. Once a TA sets a voltage vbuilt(t
= 0) = q/C in C, the response of the circuit to this impul-
sive driving starts. This response or Reaction is a slower
CC driven by vbuilt(t) itself that decays exponentially
with t as the Fluctuation of energy (Cause) is dissipated
by the CC or Effect it produces. Thus, this Reaction in-
cludes a CC through G together with a simultaneous DC
through C to rearrange the dipolar charge Q(t) = C ×
vbuilt(t) that sustains vbuilt(t) at each instant of t. Making
null iNy(t) in (4) or in Figure 8, the continuity of electri-
cal current states that this exponentially decaying CC in
G requires a similar DC in C as C loses the energy fluc-
tuation it received from the previous TA.
Calling this process Device Reaction (DR) electrical
noise becomes a random series of Action-R
king place in an electrical Admittance. This explains
and allows an easy simulation of Phase Noise in oscilla-
tors based on L-C resonators [16,17] for example. This
description in time of the noise densities


I
Sf and


V
Sf considers TA appearing randomly, both in time
and sign, at an average rate of λ TA per seconesent
tance G = 1/R as a rate of chances to dissipate
energy accordingly to (9) in Appendix III, where we have
considered these fast DC are carried by electrons inde-
pendently of one another as Johnson did in 1925 [2].
d to pr
Conduc
Figure 7. Electric al circuit that represents Johnson noise of
resistors or kT/C noise of capacitors in Thermal Equilib-
rium accordingly to our Fluctuation-Dissipation Model for
electrical noise.
Figure 8. Time-domain counterpart of the Fluctuation-Dis-
sipation Model of Figure 7 used to show the Cause-Effect con-
nection of the Fluctuation-Dissipation pair of events.

118 J.-I. IZPURA ET AL.
This view of G as λ chances per second to dissipate en-
ergy suggests the reason why the conversion A2/Hz 
2
V/Hz by the square of a resistance fails for very high R
values, as those found in [7] for the rd(v) of reverse-bi-
ased junctions with tens of VT. The high noise voltages
this conversion gives as R* would require “packets
of electrons” passing together between terminals [5] that,
contrarily to [3], we consider unlikely to occur in com-
mon devices. This led us to abandon this conversion in [7]
replacing it by the AM or Fluctuation-Dissipation Model
(FDM) for electrical noise just described, which was
used to explain two noises [5,7] that the PI of Nyquist
result in use today is unable to explain.
To use this FDM out of TE let’s consider the cases of
the BAT85 diode whose PSPICE spectra appeared in
Fi
*
gure 6(a). Recalling that for v = 0 the diode is in TE
with λ TA/s due to its two opposed Isat, the rate of TA for
i ≈ −Isat, will drop to λ/2 [5,7]. Since C only has half the
charge noise power it had in TE, we don’t have to keep

2
vt = kT/C in C, but half this value. Particularizing
(2) for these cases, we have:
 

 

 

2
0
2
0
2
12
d
VAMOUT
kTr v
Sf
1
1

1
dJ
c
J
c
fr v Cv
fv
kT
Cv f
fv





(5)
Integrating (5) from f to f we obtain:
0

2
vt =

0
2J kTCv

. Fi
g (5)
gure 6(s the th
no
in uform
b) show
e fc P
ree
ise spectra obtained usinwith thSPICE gave
Figre 6(a). They a ladder of slope 1/f whose
sum gives a 1/f noise spectrum over a band (fLO – fHI)
such that:

exp 53. 

IO HITTT
f
fnVnVVThis means
one decade of 1/f noise for a voltage span of 2.3VT (e.g.
60 mV at room T), being this the basis e 1/f noise
synthesizer that appeared in [5,7] with this FDM for
electrical noise based on Admittance.
To end, let’s justify the

0
VAM
S = (3/2) 4kTrdfw =
148.1 dB value we proposed in previous Section as the
no I, r
of th
ise for the diode with i =ll curve b) of Fig-
ure 5. Due to the Isat and +2Isat existing in this case,
we have: 3(λ/2) TA/s in C or a charge noise power that
is 3/2 times higher than the one required to keep the
kT/C noise of C by λ TA/s in TE. This means that for i
= Isat we don’t have to keep

sat eca
2
vt = kT/C V
2 in C
by using 4kTrdfw V
2/Hz as the low f value of (2). In-
stead, we have to keep 3/2 times value, whence it
can be seen the reason to write
this




032 4
VAM dfw
SkTr
6kT r .
5. Conclusions
dfw
The partial interpretation of Nyquist result today in use
1-D) noise model based on
issipation that is incomplete. A 2-D noise model using
al
no
] L. Callegaro, “Unified Derivation of Johnson and Shot
ions,” American Journal of Physics, Vol.
, pp. 438-440. doi:10.1119/1.2174034
leads to a 1-Dimensional (
D
a Complex Admittance to handle Fluctuation and Dissi-
pation of electrical energy, not only excels the aforesaid
1-D model, but also studies electrical noise accordingly
to its first Quantum Mechanical treatment due to Callen
and Welton. In this Complex model, Fluctuations and
Dissipations of electrical energy creating electrical noise
form a random series of Cause/Effect pairs in time, each
linked with an elemental charge noise of one electron.
For this Complex model of electrical noise, 1/f “excess
noise” in Solid State devices and flicker noise in ther-
moionic emitters simply are consequences of therm
ise that the 1-D noise model based on Dissipation is
unable to explain. This Complex model also shows that
the Johnson noise of resistors and the kT/C noise of ca-
pacitors, both reflect the same power 4kT/R of charge
noise in C2/s or A2/Hz, appearing thermally between two
conductors separated by some finite distance in our
physical world. The quantization of electrical noise that
results leads to an easy explanation of Phase noise in
resonant circuits of electronic oscillators.
6. References
[1
Noise Express
74, No. 5, 2006
[2] J. B. Johnson, “The Schottky Effect in Low Frequency
Circuits,” Physical Review, Vol. 26, No. 1, 1925, pp.
71-85. doi:10.1103/PhysRev.26.71
[3] G. Gomila, C. Pennetta, L. Reggiani, M. Sampietro, G.
Ferrari and G. Bertuccio, “Shot Noise in Linear Macro-
scopic Resistors,” Physical Review Letters, Vol. 92, 2004,
Article ID: 226601. doi:10.1103/PhysRevLett.92.226601
[4] H. B. Callen and T. A. Welton, “Irreversibility and Gen-
eralized Noise,” Physical Review, Vol. 83, No. 1, 1951,
pp. 34-40. doi:10.1103/PhysRev.83.34
[5] J. I. Izpura, “On the Electrical Origin of Flicker Noise in
Vacuum Devices,” IEEE Transactions on Instrumenta-
tion and Measurement, Vol. 58, No. 10, 2009, pp.
3592-3601. doi:10.1109/TIM.2009.2018692
[6] J. I. Izpura and J. Malo, “Noise Tunability in Planar Junc-
tion Diodes: Theory, Experiment and Additional Support
by SPICE,” TAEE’2006 Conference, Madrid, July 2006.
http://taee.euitt.upm.es/Congresosv2/2006/papers/2006S1
F02.pdf
[7] J. I. Izpura, “1/f Electrical Noise in Planar Resistors: The
Joint Effect of a Backgating Noise and an Instrumental
Disturbance,” IEEE Transactions on Instrumentation and
Measurement, Vol. 57, No. 3, 2008, pp. 509-517.
doi:10.1109/TIM.2007.911642

J.-I. IZPURA ET AL.
119
pp. 2520-2525.
[8] M. Sampietro, L. Fasoli and G. Ferrari, “Spectrum Ana-
lyzer with Noise Reduction by Cross-Correlation Tech-
nique on Two Channels,” Review of Scientific I
mentation, Vol. 70, No. 5, 1999,
nstru-
doi:10.1063/1.1149785
[9] J. B. Johnson, “Thermal Agitation of Electricity in Con-
ductors,” Physical Review, Vol. 32, No. 1, 1928, pp.
97-109. doi:10.1103/PhysRev.32.97
[10] H. Nyquist, “Thermal Agitation of Electric Charge in
Conductor,” Physical Review, Vol. 32, No. 1, 1928, pp.
110-113. doi:10.1103/PhysRev.32.110
[11] D. A. Johns and K. Martin, “Analog Integrated Cicuit
acher and F. C. Fitchen, “Low Noise
. Izpura, “Feedback-Induced Phase Noise
gy/1169fa.pdf
[13] C. D. Motchenb
Electronic Design,” John Wiley & Sons, New York, 1973.
[14] D. A. Bell, “Noise and the Solid State,” Pentech Press,
London, 1985.
[15] J. Malo and J. I
in Microcantilever-Based Oscillators,” Sensors and Ac-
tuators A: Physical, Vol. 155, No. 1, 2009, pp. 188-194.
doi:10.1016/j.sna.2009.08.001
[16] J. Malo and J. I. Izpura, “Feedb
Design,” John Wiley & Sons, New York, 1997.
[12] “Dual Low Noise, Picoampere Bias Current, JFET Input
Op Amp,”
http://www.datasheetcatalog.org/datasheet/lineartechnolo
ack-Induced Phase Noise
i
anish). Universidad
ppendix I
5 1 2
r R1 does not reflect a physical device.
stead it improves modelling in the reverse mode of
AT85-1
DS
1 D(IS = 2.117E-07, N = 1.016, BV
= = 1.196E-06, RS = 2.637, CJO = 1.114E-11,
VJ = 0.2013, M = 0.3868, FC = 0, TT = 0, EG = 0.69,
X
A
vn(t) in the circuit of Figure 8 the cur-
sinusoidal whereas iQ(t) is advanced
in Resonator-Based Oscillators,” Proceedings of DCIS’09
Conference, Zaragoza, November 2009, pp. 231-236.
http://www.linkpdf.com/ebook-viewer.php?url=http://dc
s2009.unizar.es/FILES/CR2/p5.pdf
[17] J. Malo, PhD Thesis, Chapter III (in Sp
Politecnica de Madrid, Madrid, pp. 70-145.
A



 
2
2
() sin
2
sin cos
E
C
UtAt
UE
A
Ct
t

t


 


SUBCKT BAT8
* The Resisto
(7)
From (6) and (7) all the power entering C leads to
flu
ts in quadrature with vn(t).
Concerning Dissipations of electrical energy, they come
from currents in-phase with vn(t). From the iP(t) =
vn(t)/R* that vn(t) produces in the resistance R
stantaneous power piP(t) entering R* is:
In
operation.
*
R1 1 2 3.6E+07
D1 1 2 B
ctuations of its energy, thus linking Fluctuations of
electrical energy with curren
.EN
* *, the in-
.MODEL BAT85-
36, IBV
 


*
2
*
sin sin
1cos2
2
iP
pt Att
R
At
R
A





(8)
Contrarily to (6) whose mean value is null because
energy enters and exits C, energy always enters R* and (8)
is the power dissipated in a resistance R*
TI = 2)
A similar model can be found in:
http://www.nxp.com/models/spicespar/BAT85.html
ppendix II
driven by sinu-
soidal voltage of amplitude A V: a positive power of
mean value Pavg = A2/(2R*) W. Thus all the instantaneous
power entering R* is dissipated. Hence,
electrical energy in C and Dissipation of electrical en-
ergy in R* are orthogonal processes linked with the Ac-
tiv
built
For a sinusoidal
ent iP(t) also isr
+90˚ respect to vn(t). Thus, the instantaneous power con-
tains Active power piP(t) = vn(t)  i
P(t) always entering
R* and Reactive power piQ(t) = vn(t)  iQ(t) entering and
leaving the Susceptance (e.g. oscillating) at 2f. Taking
vn(t) = A  sin(ωt) (ω = 2f) as a voltage existing on C
and from its related current in C: iQ(t) = C  (vn(t)/t),
the instantaneous power piQ(t) entering C is:
 



Fluctuation of
e and Reactive power in the circuit of Figure 8.
Appendix III
The idea of electrical noise as due to a random series of
Fluctuation-Dissipation events or TA-DR pairs taking
place in the Admittance of Figure 8 leads to consider the
evolution of vbuilt = q/C V created by each TA in C.
Being the sign of v positive or negative with equal
 
2
sin cos
sincos







iQ
pt AtACt
A
Ct t
(6)
On the other hand, the fluctuating electrical energy
stored in C by vn(t) will be:

J.-I. IZPURA ET AL.
120
ill be
ull (v = 0). Taking λ/2 as the average rate of positive
ate of TA is λ. For v = 0, each TA or
harge fluctuation of one electron in C will set a Fluc-
probability on average, the mean voltage in C w
n
TA, the average r
C
tuation UTA = q2/(2C) J in C. Once this Fluctuation is
completed in a short transit time

TA, its associated volt-
age vbuilt = q/C starts to drive a slower DR or the Dissi-
pation by R* of the UTA stored by the TA. Due to this,
the initial vbuilt decays with a time constant  = R*C as
shown in Figure 9(a). The spectrum of this decay will
look like the Lorentzian one of Figure 9(b), which is the
Johnson noise v(t) of the circuit of Figure 7 coming from
a random series of pulses like that of Figure 9(a), each
following its own TA (Carson’s Theorem).
Since the noise power N dissipated in R* (the kT/C
noise of C divided by R*) has to dissipate the energy
fluctuations of λ TAs per second on average, we have:

2
*
*2*
24
2
2
kTqkT kT
NRqq
C RCq R



 (9)
Equation (9) shows that the Resistance R* of a resistor
or capacitor in TE is inversely proportional to the λ op-
portunities per unit time it has to dissipate ene
shows that the noise density 4kT/R* A2/Hz preserving the
kT/C noise of C is the density of shot noise due to the λ
TA’s per unit time taking place in this device.
rgy. It also
Thus, the shot noise 2qITA A
2/Hz of the current I
λq associated to the λ TAs per unit time of this devi
the source of its electrical noise, no matter if we call it
Jo
happens if we change the
co
his agrees with (9), where 10 times
possible blockage by the conducting material between
them. This is solved, however, by considering that a free
electron in a Quantum State (QS) of the Conduction
Band (CB) has a wavefunction extending over the whole
material between plates. This would allow an electron to
jump from a contact to this QS as soon as it is left empty
by the electron that, occupying it previously, has been
captured by the far contact (Collector). Thus, a QS or
energy level of the CB would be a sort of tunnel for the
fast transit of each electron between ohmic contacts
cladding n-type semiconductor material for example.
Used to electrons transiting between electrodes in
vacuum devices that are collected a short transit time 
T
after their emission, the above process looks reversed: an
electron of the CB is captured by the Collector a short
time 
T before another electron is emitted from the Emit-
ter contact to the empty QS of the CB. Processes where
electrons emitted from a contact to empty QS of the CB
are subsequently captured by the other contact acting as a
Collector of electrons are equally possible.
TA =
ce is
hnson noise of its resistance R* or kT/C noise of its
capacitance C. This deep connection between “shot” and
Johnson noises (also found by other scientists [1]) is the
charge noise existing in the capacitance C of a resistor or
capacitor in TE due to its λ TA-DR pairs per unit time
that are shown in Figure 10.
Since each DR has a CC and a DC giving a charge
fluctuation of q C each in C and they are uncorrelated in
time due to their orthogonal character in f-domain, the
mean square charge noise per second (charge noise
power) existing in C due to DR is: 2(λq2) = 4kT/R* C2/s.
This explains the alternative units used in Figure 7 to
reveal neatly the same charge noise underlying Johnson
and shot “noises”.
It is worth studying what
nducting material between plates in Figure 1 to reduce
its R* to R*/10 while keeping the same ε. Since C does
not vary its kT/C noise will remain, but the voltage de-
cays of Figure 9(a) will be ten times faster, thus having
a ten times broader spectrum (Figure 9(b)). Since the
voltage vbuilt = q/C decays ten times faster with t, there
must be ten times more TA (10λ) to sustain the same
kT/C V
2 in time. T
lower R* at the same T requires a 10 times higher rate of
TA or 10 times more charge noise due to TA. Since this
happens no matter the material we use, the presence of
solid matter between contacts doesn’t change the nature
of the TA in our FDM: a Charge Noise of one electron.
Although single electrons jumping between plates in
vacuum is well know [2], this is not so for electrons do-
ing it between contacts in Solid-State devices due to their
v
n
(t)
4 kTR
1/f
2
τ = CR
*
Frequency
(a) (b)
Figure 9. (a) Impulse response of the circuit of Figure 8
driven by current iNy(t) and taking v(t) as its output signal.
(b) Bode plot (modulus) of the Lorentzian spectrum of v(t)
mirroring the spectral energy content of the impulse shown
in Figure 4.
Figure 10. Charge noises in the contacts of a resistor or
capacitor due to the (Thermal Action)/(Device Reaction)
dynamics described in the te xt.