Paper Menu >>
Journal Menu >>
 American Journal of Computational Mathematics, 2011, 1, 129-133 doi:10.4236/ajcm.2011.12013 Published Online June 2011 (http://www.scirp.org/journal/ajcm) Copyright © 2011 SciRes. AJCM Magneto Hydrodynamic Orthogonal Stagnation Point Flow of a Power-Law Fluid toward a Stretching Surface Manisha Patel1, Munir Timol2 1Department of Mat hem at ic s, Sarvajanik College of Engineering & Technology, Surat, India 2Department of Mat hem at ic s, Veer Narmad South Gujarat University, Surat, India E-mail: {manishapramitpatel, mgtimol }@gmail.com Received April 27, 2011; revised May 25, 2011; accepted June 5, 2011 Abstract: Steady two dimensional MHD stagnation point flow of a power law fluid over a stretching surface is inves- tigated when the surface is stretched in its own plane with a velocity proportional to the distance from the stagnation point. The fluid impinges on the surface is considered orthogonally. Numerical and analytical solutions are obtained for different cases. Keywords: Stagnation Point Flow, Galerkin’s, Finite Difference Method, Stretching Surface. 1. Introduction The stagnation point is a point on the surface of a body submerged in a fluid flow where the fluid velocity is zero. Stagnation flow, describing the fluid motion near the stagnation region, exists on all solid bodies moving in a fluid. The stagnation region encounters the highest pres- sure, the highest heat transfer, and the highest rates of mass deposition. The stud y of flow over a stretching sur- face has generated much interest in recent years in view of its numerous industrial applications such as extrusion of polymer sheets, continuous stretching, rolling and manufacturing plastic films and artificial fibers. The flow near a stagnation point has attracted many investigations during the past several decades because of its wide ap- plications such as cooling of electronic devices by fans, cooling of nuclear reactors, and many hydrodynamic processes [1-5]. The two-dimensional flow of a fluid near a stagnation point was first examined by Hiemenz [6], who demon- strated that the Navier-Stokes equations governing the flow can be reduced to an ordinary differential equation of third order using similarity transformation. Later the problem of stagnation point flow was extended in nu- merous ways to include various physical effects. The results of these studies are of great technical importance, for example in the prediction of skin-friction as well as heat/mass transfer near stagnation regions of bodies in high speed flows and also in the design of thrust bearings and radial diffusers, drag reduction, transpiration cooling and thermal oil recovery. Axisymmetric three-dimen- sional stagnation point flow was studied by Homann [7]. Either in the two or three-dimensional case Navier- Stoke’s equations governing the flow are reduced to an ordinary differential equation of third order using a simi- larity transformation. In hydromagnetics, the problem of Hiemenz flow was chosen by Na [8] to illustrate the so- lution of a third-order boundary value problem using the technique of finite differences. An approximate solution of the same problem has been provided by Ariel [9]. At- tai [1] has made an analysis of the steady lamin ar flow in a porous medium of an incompressible viscous fluid im- pinging on a permeable stretching surface with heat gen- eration. The steady magneto hydrodynamic (MHD) mixed convection stagnation point flow towards a verti- cal surface immersed in an incompressible micropolar fluid with prescribed wall heat flux was investigated by Bachok et al. [4]. They have transformed the governing partial differential equations into a system of ordinary differential equations, which is then solved numerically by a finite-difference method. Hayd et al. [2] have stud- ied the boundary layer equations for axisymmetric point flow of power-law electrically conducting fluid through a porous medium with transverse magnetic field. McLeod and Rajagopal [10] have discussed the uniqueness of the exact analytical solution of the flow of a Newtonian fluid due to a stretching boundary. On the other hand, Rajagopal et al. [10,11] obtained an approximate ma- thematical solution of the viscoelastic boundary layer flow over a stretching plastic sheet and studied the flow 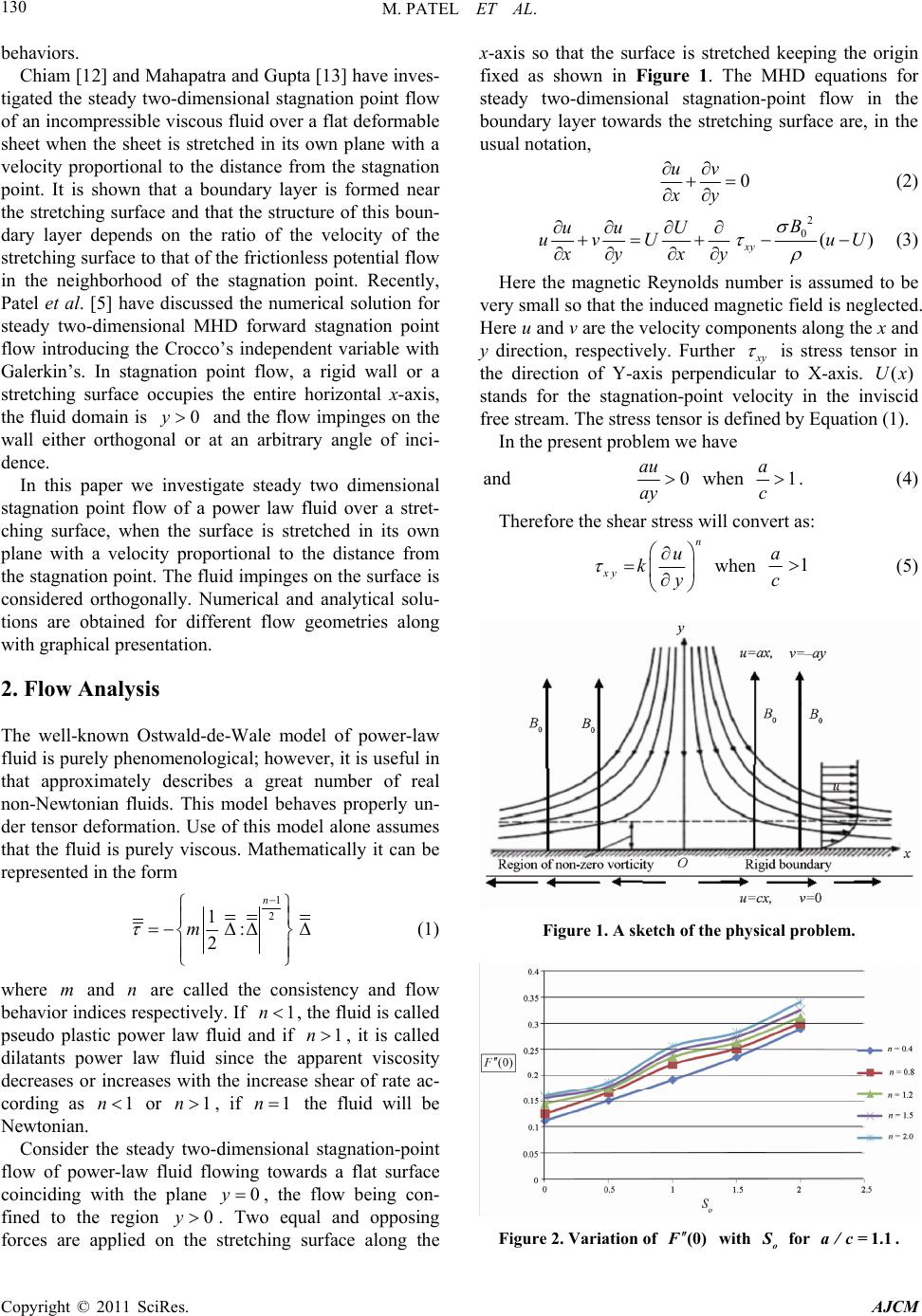 M. PATEL ET AL. Copyright © 2011 SciRes. AJCM 130 behaviors. Chiam [12] and Mahapatra and Gupta [13] have inves- tigated the steady two-dimensional stagnation point flow of an incompressible viscous fluid over a flat deformable sheet when the sheet is stretched in its own plane with a velocity proportional to the distance from the stagnation point. It is shown that a boundary layer is formed near the stretching surface and that the structure of this boun- dary layer depends on the ratio of the velocity of the stretching surface to that of the frictionless potential flow in the neighborhood of the stagnation point. Recently, Patel et al. [5] have discussed the numerical solution for steady two-dimensional MHD forward stagnation point flow introducing the Crocco’s independent variable with Galerkin’s. In stagnation point flow, a rigid wall or a stretching surface occupies the entire horizontal x-axis, the fluid domain is 0y and the flow impinges on the wall either orthogonal or at an arbitrary angle of inci- dence. In this paper we investigate steady two dimensional stagnation point flow of a power law fluid over a stret- ching surface, when the surface is stretched in its own plane with a velocity proportional to the distance from the stagnation point. The fluid impinges on the surface is considered orthogonally. Numerical and analytical solu- tions are obtained for different flow geometries along with graphical presentation. 2. Flow Analysis The well-known Ostwald-de-Wale model of power-law fluid is purely phenomenological; however, it is useful in that approximately describes a great number of real non-Newtonian fluids. This model behaves properly un- der tensor deformation. Use of this model alone assumes that the fluid is purely viscous. Mathematically it can be represented in the form 1 2 1: 2 n m (1) where m and n are called the consistency and flow behavior indices respectively. If 1n, the fluid is called pseudo plastic power law fluid and if 1n, it is called dilatants power law fluid since the apparent viscosity decreases or increases with the increase shear of rate ac- cording as 1n or 1n, if 1n the fluid will be Newtonian. Consider the steady two-dimensional stagnation-point flow of power-law fluid flowing towards a flat surface coinciding with the plane 0y , the flow being con- fined to the region 0y. Two equal and opposing forces are applied on the stretching surface along the x-axis so that the surface is stretched keeping the origin fixed as shown in Figure 1. The MHD equations for steady two-dimensional stagnation-point flow in the boundary layer towards the stretching surface are, in the usual notation, 0 uv xy (2) 2 0() xy B uu U uvU uU xy xy (3) Here the magnetic Reynolds number is assumed to be very small so that the induced magnetic field is neglected. Here u and v are the velocity components along the x and y direction, respectively. Further x y is stress tensor in the direction of Y-axis perpendicular to X-axis. ()Ux stands for the stagnation-point velocity in the inviscid free stream. The stress tensor is defined by Equation (1). In the present problem we have and 0 au ay when 1 a c. (4) Therefore the shear stress will convert as: n xy u ky when 1 a c (5) Figure 1. A sketch of the physical problem. Figure 2. Variation of (0)F with o S for = 1.1a/c .  M. PATEL ET AL. Copyright © 2011 SciRes. AJCM 131 Table 1. n 0 o S 0.5 o S 1.0 o S 1.5 o S 2.0 o S 0.4 0.1123 0.1252 0.1445 0.1564 0.1601 0.8 0.1512 0.1668 0.1748 0.1799 0.1869 1.2 0.1924 0.2214 0.2356 0.2455 0.2662 1.5 0.2358 0.2514 0.2636 0.2741 0.2852 2.0 0.2897 0.2999 0.3121 0.3255 0.3412 Table 2. n 0 o S 0.5 o S 1.0 o S 1.5 o S 2.0 o S 0.4 1.2216 1.3625 1.4886 1.6289 1.7865 0.8 1.0023 1.0423 1.0858 1.1821 1.3226 1.2 0.8984 0.9672 1.0115 1.1000 1.2101 1.5 0.8864 0.9355 1.0021 1.0552 1.1001 2.0 0.8876 0.9301 0.9864 0.9945 1.0477 Table 3. n 0 o S 0.5 o S 1.0 o S 1.5 o S 2.0 o S 0.4 3.8771 4.1332 4.4755 4.8163 5.2445 0.8 2.3854 2.5446 2.5845 2.8354 2.8714 1.2 1.9328 1.9454 2.0023 2.1426 2.1735 1.5 1.7001 1.7537 1.8817 1.9583 1.9966 2.0 1.5481 1.5841 1.6120 1.6526 1.6998 Table 4. Results of finite difference method of Case-I. No. of iteration 0 o S 0.5 o S1.0 o S 1.5 o S2.0 o S 1 1.02326 1.2326 1.2326 1.2326 1.2326 2 1.1688 1.3593 1.5393 1.7882 1.8385 3 1.1743 1.3637 1.5407 1.7890 1.8339 4 1.1715 1.3618 1.5392 1.7662 1.8328 5 1.1717 1.3621 1.5394 1.7914 1.8330 6 1.1717 1.3620 1.5394 1.7914 1.8330 Now the momentum Equation (3) become, in non-di- mensional fo r m, when 1 a c 2 0() nB uu UKu uvU uU xy xyy (6) The boundary conditions are: , 0 y0ucxv at (7) (), , yuU xaxvayat (8) where a and c are positive constants. Introducing stream function (, ) x Y , where uy and =v x (9) Following Labropulu [3], we assume that ()cxF y (10) Using Equations (9) and (10) into the Equation (6), we obtained 12 ()()() () 1 nn nF yFyFyF y n 2 2 2 () ()0 oo aa FySFyS cc (11) with the boundar y conditions: (0) 0F , (0) 1F , ()a Fc (12) where 2 0 o B Sc is the magnetic parameter. Case-I: Newtonian fl uid: cons ider 1n and /1ac Equation (11) is converted in the following equation 2 ()()()()()1 0 oo FyFyFy FySFy S (13) with the boundar y conditions: (0) 0F , (0) 1F , ()a Fc (14) Case-II: if we consider case for 1n, and let 0U (i.e. 0a ) then the Equation (11) is converted in 2 ()()()()() 0 o Fy FyFyFySFy (15) Subject to the boundary conditions; (0)0,(0)1,( )0FFF (16) It is interesting to note that the above BVP Equation (15) has a simple analytic solution of the form Figure 3. Variation of (0)F with o S for = 1.5a/c . Figure 4. Variation of (0)F with o S for = 2.0a/c .  M. PATEL ET AL. Copyright © 2011 SciRes. AJCM 132 Figure 5. Variation of (0)F with o S for =1a/c , =1n. Figure 6. Variation of () F y with y . 1 ( )[1exp()] F ypy p (17) where 1/2 0 (1 )pS Method of solution: The transformed momentum Equation (11) is solved using Galerkin’s method after introducing Crocco’s variables [5,14]. The equation for Case-I (Equation (13)) is solved by T. Y. Na [8] using Finite difference method the graphical presentation of those tabular values ( Table 3) is shown in Figu re 2. And the equation of Case-II (Equation (15)) is solved analyti- cally. Results and discussion: The computed variation of 0F with o S and n is summarized in Tables 1 and 2 for /1.1, 1.5ac and 2.0, respectively. It can be con- clude (from the above Tables 1-3, Figures 2-4) that fo r a fixed value of o S, 0F increases with increase in n in a small neighbourhood of /1ac then it decreases for other val ues of a/c. Fr om Tables 1-3, it is clear that for a fixed value of n and /ac, the value of 0F de- creases with increase in o S. This behaviour may perhaps be attributed to the change in the character of the flow as /ac changes its values. It is interesting to note that when the velocity of the stretching surface is equal to the velocity of the inviscid stream ac , Equation (16) ad mit to the ex act analytic solution () F yy . From this we can infer that when ac , the velocity distribution near the stretching sur- face is the same as athat of a flow away from the surface so that no boundary layer is formed near the surface. It should be mentioned here th at when , the flow is not fric- tionless in a strict sense. In fact in this case the friction is uniformly distributed and does not, therefore, affect the motion. If we consider 1n then the entire flow geometry is reduced in Newtonian fluid, which is discussed as a Case-I with ac (i.e. /1ac, Table 4, Figure 5). For that case 0F increases with increase in the val- ue of o S for a fixed value of 1n. If we consider stream velocity is zero 1n then the flow is treated as a uniform stagnation point flow, in this case F y decreases with increase in y for a fixed value of o S. The graphical representation is shown in Figure 6. 3. References [1] H. A. Attai, “Stagnation Point Flow towards a Stretching Surface through a Porous Medium with Heat Generation,” Turkish Journal of Engineering & Environmental Scien- ces, Vol. 30, No. 5, 2006, pp. 299-306. [2] F. M. Hayd and I. A. Hassanien, “Magnetohydrodynamic and Constant Suction/Injection Effects of Axisymmetric Stagnation Point Flow and Mass Transfer for Power-Law Fluids,” Indian Journal of Pure and Applied Mathematics, Vol. 17, No. 1, 1986, pp. 108-120. [3] F. Labropulu and D. Li, “Stagnation Point Flow of a Second-Grade Fluid with Slip,” International Journal of Non-Linear Mechanics, Vol. 43, No. 9, 2008, pp. 941-947. doi:10.1016/j.ijnonlinmec.2008.07.004 [4] B. Norfifah and I. Anuar, “MHD Stagnation-Point Flow of a Micropolar Fluid with Prescribed Wall Heat Flux,” European Journal of Scientific Research, Vol. 35 No. 3, 2009, pp. 436-443. [5] M. Patel and M. G. Timol, “Numerical Solution of Steady Two-Dimensional MHD forward Stagnation Point Flow,” Applied Mathematical Science, Vol. 3, No. 4, 2009, pp. 187-193. [6] K. Hiemenz, “Die Grenzschicht an Einem in Den Gleich- formingen Flussigkeitsstrom Eingetauchten Graden Krei- szylinder,” Dingler’s Polytechnic Journal, Vol. 326, 1911, pp. 321-324. [7] F. Homann, “Der Einfluss Grosser Zahigkeit bei der Stromung um den Zylinder und um die Kugel,” Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechani, Vol. 16, No. 3, 1936, pp. 153-164. doi:10.1002/zamm.19360160304 [8] T. Y. Na, “Computational Methods in Engineering Boundary Value Problems,” Academic Press, New York, 1979.  M. PATEL ET AL. Copyright © 2011 SciRes. AJCM 133 [9] P. D. Ariel, “Hiemenz Flow in Hydromagnetics,” Acta Mechanica, Vol. 103, No. 1-4, 1994, pp. 31-43. [10] K. R. Rajagopal, T. Y. Na and A. S. Gupta, “A Non Sim- ilar Boundary Layer on a Stretching Sheet in a Non-Newtonian Fluid with Uniform Free Stream,” Jour- nal of Mathematical Physics, Vol. 21, No. 2, 1987, pp. 189-200. [11] K. R. Rajagopal, T. Y. Na and A. S. Gupta, “Flow of a Viscoelastic Fluid over a Stretching Sheet,” Rheologica Acta, Vol. 23, No. 2, 1984, pp. 213-215. doi:10.1007/BF01332078 [12] T. C. Chiam, “Stagnation-Point Flow towards a Stretch- ing Plate,” Journal of the Physical Society of Japan, Vol. 63, No. 6, 1994, pp. 2443-2444. doi:10.1143/JPSJ.63.2443 [13] T. R. Mahapatra and A. S. Gupta, “Heat Transfer in Stagnation-Point Flow towards a Stretching Sheet,” Heat Mass Transfer, Vol. 38, No. 6, 2002, pp. 517-521. doi:10.1007/s002310100215 [14] T. C. Chiam, “Solution for the Flow of a Conducting Power-Law Fluid in a Transverse Magnetic Field and with a Pressure Gradient Using Crocco Variables,” Acta Mechanica, Vol. 137, No. 3-4, 1999, pp. 225-235. Nomenclature: u, v – velocity components in X, Y directions respec- tively U – main stream velocity in X direction a, c – positive constants ,, ij – usual shear stress tensor , ij e – usual rate of deformation tensor/ Strain rate component y x – stress tensor in the direction of X-axis perpen- dicular to Y-axis. K – kinematic Viscosity m – Physical constant n – flow behavior indices 0 B – Imposed magnetic field M HD – Magneto hydro dynamics – field density – Electrical conductivity p C – Specific heat – Stream function F – Similarity function o S – Magnetic parameter – 2 0 B |

