Journal of Modern Physics, 2011, 2, 564-571
doi:10.4236/jmp.2011.26066 Published Online June 2011 (http://www.SciRP.org/journal/jmp)
Calculation of Complete Absorption and Intensity of
Optical Radiation Spectrum of HeI (
 = 5875 Å) with
Fine Structure
Reda A. El-Koramy1, Nazer A. Ashurbecov2
1Physics Department, Faculty of Science, Assiut University, Assiut, Egypt
2Department Physical Electronics, Daghestan State University, Daghestan, Russia
Received February 13, 2011; revised April 24, 2011; accepted May 13, 2011
Abstract
Theoretical calculations which account for the complete absorption and intensity for the optical radiation He
I (  = 5875 Å) spectral line with fine structure of the transition 23P2,1,0 - 33D3,2,1 during He nanosecond dis-
charge are presented. For different values of the absorption parameter ( 
0ℓ), the absorption quantity A of the
three components distorted as a result of reabsorption multiple process has been numerically obtained and
graphically presented. The theoretical results for small values of 
0ℓ (≤ 4) give a good agreement with the
experimental data in literature.
Keywords: Optical Radiation Spectrum, Complete Absorption, Intracavity Laser Spectroscopy, Simpson’s
Formula, Computer Processing
1. Introduction
While the classical theories gave a semi-quantitative ex-
planation for the interaction between matter and radiation,
no precise and general treatment was possible before the
advent of quantum theory. In principle, the quantum the-
ory of matter allows one to calculate the various energy
levels that any given atom or ion may possess. However,
as long as classical electromagnetic theory is used, emit-
ted, absorbed or scattered radiation is still ambiguous.
Much detailed work remains to be done to elucidate the
nature of numerous approximate treatments and to assess
the ranges of applicability and the degree of approxima-
tion that has been achieved. The variation of inter-atomic
(intermolecular) forces as a function of inter-atomic (in-
ter-molecular) distance has been increasingly attracting
the attention not only of theoretical and experimental
physicists but also of those who are working on certain
basic problems of chemistry, genetics and astrophysics.
Plasma-broadened and shifted spectral line profiles
have been used for a number of years as a basis of an
important non-interfering plasma diagnostic method. The
numerous theoretical and experimental efforts have been
made to find solid and reliable basis for this application.
This technique became, in some cases, the most sensitive
and often the only possible plasma diagnostic tool. In the
early 1960s a number of attempts [1-3] were made to
improve and to check experimentally existing theories of
spectral line broadening by plasmas. Most of these early
works were concerned with the Stark broadening of hy-
drogen lines. Owing to the large, linear Stark effect in
hydrogen, these studies were very useful for plasma di-
agnostic purposes. However, it is not always convenient
to seed plasma with hydrogen, and sometimes this is not
possible.
Although the theory of Stark broadening was used on-
ly as a consistency check in the study of the influence of
ion dynamics to the width and shift of visible helium
lines in low electron density plasmas, an important con-
clusion was derived from the comparison with the results
of semiclassical calculations [4,5]. This conclusion, which
may be used for plasma diagnostic purposes with an av-
erage estimated accuracy of ±20% and ±30% for a neu-
tral atom and singly charged ion lines, respectively, led
to the fact that the total width and shift is a sum of the
electron and all ion impact widths. On the basis of com-
parison of selected data in [4] and calculations for the
energy positions and widths of singlet and triplet (even
and odd) resonances of helium-like (Z = 2 – 10) systems
lying between the n = 2 and n = 3 thresholds [6], an at-

R. A. EL-KORAMY ET AL.
565
tempt was made to extend these works and to identify
lines of various elements which may be used with higher
accuracy for plasma diagnostic purposes [7].
The study of emission radiation from atoms (or ions)
in plasma constitutes an important area of plasma diag-
nostics. From the experimental point of view, plasma is
sometime optically thick to its emission lines, then, the
emitted photons may be absorbed within the plasma.
Over the past, more than thirty years period of formation
and development of spectroscopic techniques, selective
intra-cavity laser spectroscopy (ICLS) provides the pos-
sibility of simultaneously recording the profiles of a
number of spectral lines and bands in probing both
brightly emitting and nonradiative objects. Also, of par-
ticular interest, ICLS combines high sensitivity in de-
tecting absorption centers [8-11] and, so, characterizes
the integral absorption coefficient within the frequency
limits of the absorption line [12,13]. Furthermore, transi-
tion probabilities and atomic lifetimes [4] and optical
absorption and reflectance [14] have been reported. Pre-
dicted He I line intensities and line ratios in microwave-
generated plasmas and from a recently developed colli-
sional-radiative model were compared with experiment
[15,16] It has been concluded that the intensity of triplet
lines is strongly affected by the local metastable state
(21S and 23S) populations and the initial metstable frac-
tion plays an important role in determining line intensi-
ties. In spite of there has been a lot of work done within
the past decade, both theoretical and experimental, were
given [17-23]; and, recently, resonance parameters and
autoionization widths of the doubly excited states of the
helium isoelectronic sequence [24] have been studied,
however, there are some important aspects of the subject
which have not been clearly discussed. Presently due to
progresses of computer processing, the need of another
review is quite obvious. The present work is merely to
aid in this process of focusing thought upon crucial is-
sues.
The present work is intended to derive analytic ex-
pressions for calculating dependencies of complete ab-
sorption and intensity of radiation spectrum on optical
depth along the line sight in a nanosecond gas discharge.
We report results of complete absorption for the optical
radiation of HeI (  = 5875 Å) spectral line with fine
structure of the transition 23P2,1,0 - 33D3,2,1 through He
nanosecond discharge.
2. Theoretical Analysis
2.1. Advanced Spectroscopic Treatment
Spectroscopy is a powerful tool to diagnose plasmas and
has played and will continue to play a major role in
plasma physics research. Interest in line broadening has
been renewed in the last few years because of the large
amount of recent plasma work. The line shapes obtained
by spectroscopic examination of the emission of plasma
can yield information about plasma density.
2.2. Doppler Producing Broadening and Shift of
Spectral Lines
The line profiles emitted from the plasma are governed
by Doppler and Stark broadenings. Doppler effects give
rise to further broadening rather than ones. So, other
broadening mechanisms can be neglected for our plasma
condition, which represent a typical emission spectrum
from laboratory plasma. It consists of continuous brems-
strahlung and recombination radiation superposed by line
radiation. We now visualize the plasma to be homoge-
nous and to increase steadily its optical depth in the di-
rection of observation. The spectral radiance will in-
crease until it reaches the Planck value of the blackbody
emission according to the existing temperature. We con-
sider an emitting atom in motion to infinity and reduce
temperature to the point where, classically at least, no
translational motion exists. Every influence exerted on a
radiating or absorbing atom (or molecule) modifies its
spectral lines in one way or another. The effect of its
own thermal motion, which broadens the lines statisti-
cally, is known as the Doppler Effect. In the case of
emission or resonance absorption, the process of radia-
tion damping, or a finite width of each of the two energy
levels associated with spectral lines, is responsible for
the natural width. If the atom is in a gas of the same kind,
the spectral lines are broadened and sometimes are
shifted with asymmetry of the line shape. The essential
cause of line broadening lies in the finite difference of
interaction energies of the radiating atom, in the initial
and final states involved in the radiation process, with a
colliding atom. When the interacting atoms, one of
which is excited, are identical, a resonance case will be
established. This resonance introduces twofold degener-
acy (symmetric and anti-symmetric).
As it is known that the intensity of emission (absorp-
tion) is defined as the radiant energy emitted (absorbed),
which penetrates a unit area in a plasma volume in unit
time per unit solid angle perpendicular on the area, and,
per unit of frequency . The so-defined intensity encom-
passes radiation of all frequencies and hence, should be
called “complete intensity”. If one measures the spectral
intensity of one line and its vicinity, the frequency (or
wavelength) gives information that a certain element is
present in a certain stage of ionization. The absorption
and emission of a spectral line are determined by the
population of the lower and the upper quantum level re-

566 R. A. EL-KORAMY ET AL.
spectively, and, by Einstein’s probabilities. For the cal-
culation of the line intensities emitted from plasma, and,
vice versa, for spectroscopic plasma diagnostics, the
knowledge of the transition probabilities of all investi-
gated lines is indispensable.
We suppose, our emitting atom has a velocity compo-
nent
 in the line of sight of observer. Now, if the atom is
emitting a spectral line radiation of wavelength

0, and a
frequency

0, Doppler effect causes our observer to re-
ceive radiation of wavelength
 ', such that
01c








, (1)
assuming  c (light velocity). 
Velocity distribution in the line of sight is given by the
Maxwellian distribution factor as exp [−βξ2], where
2
M
kT

, (2)
[M-the atomic mass, k –Boltzmann’s constant and T is
the absolute temperature].
From (1), it can be written

2
22
0

 
. (3)
In the last relation 
0 may now be considered as the
wavelength corresponding to the maximum intensity of
the line (line center), and 
 as the frequency whose
displacement corresponds to the line of the sight velocity
 , or in other words, the line shift. Although there are
some kinds of broadenings (such as Stark, van der
Waals, ...etc), Doppler effects due to the relative motion
of radiating systems give rise to further broadening ra-
ther than ones. If the velocities of radiating system have
thermal distribution, collisions are negligible; otherwise,
and furthermore, if one arbitrarily equates the line center
intensity to unity, the Doppler effect alone produces a
distribution of intensities over the spectral line which
may be represented by the following form, using (3)

2
2
0
exp 2
M
II kT



 



. (4)
Doppler broadening results in a Gaussian line shape,
whose half-width

D is defined as the frequency width
of the spectral line at an intensity I equivalent to one -
half the maximum intensity (I0/2). Accordingly, using (4),
we can write
12
0
2ln2
2
D
RT
M
c






, (5)
where R represents the gas constant.
It may be remarked that the emitted spectrum of any
homogenous source becomes more and more continuous
(smooth) as the depth of the source increases. This is due
to the fact that the strongest lines tend to be reabsorbed,
then the weaker ones and eventually also parts of the
continuum, until the spectrum resembles a blackbody
continuum.
2.3. Spectroscopic Treatment of Radiation
Absorption
An observer collects radiation along the line of the sight
and, in general, absorption of radiation will occur, and
this has to be taken into account. This leads, neglecting
scattering, to the following treatment. We assume an
absorption line at the frequency  with a dispersion pro-
file and frequency—dependent absorption coefficient
 (  ), such that its line width is much smaller than the
generation line width. The generation spectrum corre-
sponding to the entire pulse exhibits a valley which also
has the dispersion profile described by the Lambert-
Beers relation
 
0
0
,exp d
I
It

   
 t (6)
Here: I(
 ) represents the spectral radiance intensity of
generation in the modes with narrow-band selective ab-
sorption (in the absence of saturation) (sometimes re-
ferred to as flow-out) recording from the absorbent 2 , as
shown in the schematic diagram of Figure 1; I0(
 ,t) =
I0f(t) - the spectral radiance intensity of generation in the
absence of additional selective absorption, f(t) is a func-
tion describing the shape of the radiation-pulse envelope
in the spectral region (flow-in) at the absorbent surface 2
comes out of the radiant source 1; and = (ctx/L) is the
effective thickness of the absorbing layer at the moment
of time t, x is the length of the absorbent, and L is the
cavity base. It must pointed out here that, in the particu-
lar case where a laser pulse can be approximated by a


Figure 1. Schematic diagram of the illustrated positions of
the 1—radiant source and 2—absorbent surface of a speci-
men.

R. A. EL-KORAMY ET AL.
567
function which describes a rectangle, so,

1 0
0 .
t
ft t






Let us consider basic dependences and relationships
which rather adequately describe intracavity absorption
in pulsed lasers which are useful for measuring the mag-
nitude of the frequency-dependent absorption introduced
into the cavity. Under the conditions where the apparatus
width of the spectral instrument used for recording the
generation spectra of a laser with a selectively absorbing
medium in the cavity is commensurable with the actual
width of the absorption line or exceeds it, it is advisable
to apply the method of complete absorption [13]. How-
ever, the basic aspects and special features of the meas-
urements of the spectrum-integral absorption in the ab-
sorption line were given previously [11,5].
The complete line absorption and intensity depend es-
sentially on  (  ) and . 
The quantity of the complete absorption A of radiation
is defined as:

0
1,.
A
IIt   
 
(7)
2.4. Limits of the Presented Treatment
For simplicity, we restrict our attention to the following
conditions concerning the spectrum generation:
1) We consider that the radiant source 1 has a rectan-
gular form within its interval  , such that outside this in-
terval no radiation may be emitted or absorbed, i.e.;
 
0
0
0
,0 .
It
It t









2
.
2) On the other hand, since the absorption spectrum is
different over the profile of the absorption line, the inte-
gration given in (6) extends over a limited frequency
range of the absorbed line, such as
 
01
0
2
,0 .
I
It









Here (

2 -

1) represents the frequency optical depth
along the line of the sight, at which Doppler effect ex-
hibits a constant value. Therefore, Equation (6) becomes:
 
2
1
0exp dII



  



  (8)
If the radiated layer 1 and the absorbed one 2 (Figure
1) are identical in all its parameters [temperature, pres-
sure, thickness and energy-level distribution function as
well as the same identical atoms (or molecules) …etc],
so, for small values of 
0 and using Equation (8), Eq-
uation (7) takes the form [26]






2
1
2
1
0
0
d, or
1exp d,
II
AI
A











 



(9)
taking into consideration that  (  ) has the following ex-
pression [5]


2
0
0exp 2.7726,
D

 















(10)
where

0 represents the absorption coefficient in the
spectral line center and  
D is, from its definition, taken
at ordinate  (  ) = 1/2 
0.
3. Results and Discussion
The choice of a transition involving only levels with well
understood kinetics for this study is essential. The helium
(He) discharge is one of the most thoroughly studied
discharge systems [27]. We give now certain analysis
needed for the calculation of the complete absorption of
the fine structure HeI (
 = 5875 Å) spectral line, ob-
tained in a laboratory work [28] during a nanosecond He
discharge, due to the optical transition 23P2,1,0 - 33D3,2,1,
schematic representation diagram of which is shown in
Figure 2. This transition is ideal because of its conven-
ient wavelength (
 = 5875 Å), and most of the kinetics of
the 33D level [29], the 23P level [30,31], and other
nearby levels [32] are known. The energy levels 3D3,2,1 of
the state 3D practically are coincident (splitting of that
state consists of hundreds and thousands submultiplet
fractions of percents) whereas the state 2 3P is reversal. By
the rule of brightness, the intensities of 2 3P components
Figure 2. Schematic representation diagram of: a) the en-
ergy levels of the spectral line transition 2 3P2,1,0 - 3
3D3,2,1 of HeI (λ = 5785 Å), illustrating its fine structure
and; b) the intensity ratios (1:3:5) of its components with
respect to their statistic a l weights.

568 R. A. EL-KORAMY ET AL.
are in the ratios of 1:3:5, respectively, with their statisti-
cal weights of the levels 23P0, 23P1 and 23P2.
On the other hand, these ratios are the same as that
observed between the absorption coefficients in the line
center of each individual component. So, the relationship
between 
0 and I0(
 ) of the stimulated emission at the
frequency of the absorption band edge of the transition
depends on the relative population of the energy levels
(Nm/Nn). Since the two energy levels m and n have a fine
structure, for individual components i
 j, it may have the
following relation [33]
 
2
3
00
2
j
i
j
i
ji ij
N
g
cI
gN
h
 ij , (11)
where
 (0) and I(0) represent the absorption coefficient
and intensity at the line center.
It is more easily established a resonance distribution
for the nearest superposition sublevels rather than that
for faraway remaining ones. Since, the frequencies of the
three components, of which are close to each other, it can
be used for the following substitutions:
,
ji
j
mi
mn
gg
NNN
gg

n
N
and, therefore, Equation (11) may be re-written as
 
2
3
00
2
nm
j
ii
mn
ij
gN
cI
gN h
 j (12)
If m
n
N
N is constant, the absorption coefficients of the
spectral line components are proportional to its bright-
ness. This partial fulfillment of Boltzmann’s law also
allows one to keep the processing results of measure-
ments to be carried out for lines with a fine structure
since Nm/Nn is constant during the experimental condi-
tions. Neglecting splitting of the upper-level, so, for the
summation of the transition probability Anm and the tran-
sition probability of the individual components, it may be
written in the following form
j
nj nm
j
j
a
AA a , (13)
where An1:An2:An3 = a1:a2:a3 = 1:3:5 ; and, according to
the rule of brightness, then aj = gj, where gj represents
the statistical weights of the sub-levels on which the lev-
el -m splits.
In the experimental conditions, one mirror has been
used for the radiant source 1. So, if we suppose that I'
represents the intensity of the flow-in radiation, then,
taking into account the re-absorption and loss on the
front window, rI' represents the reflected flow-in inten-
sity, where r is called the reflection coefficient of the
mirror. We suppose that the defined relationships of ini-
tial intensities of the three components and their absorp-
tion coefficients in the line center, respectively, are as
follows
01 0203123
:: ::;
I
II aaa
0102031 2 3
:: ::bbb;

 
i.e., generally speaking,
00
,
j
jj j
I
CaC b




where C and C' are constants in the experimental condi-
tions, therefore, the intensity distribution function of the
j-th component takes the following form [33]


2
00
2
0
00
1exp exp
j
jj
j
jj
I
a
C
rCbc
Cb







 









 








.
(14)
Accordingly, the intensity distribution function of the
sum flow-in radiation from all components can be writ-
ten as


2
00
2
0
00
1exp exp
jj
j
jjj
I
a
C
rCbc
Cb



















 



 




(15)
On the other hand, during the passing of the absorbent
source 2, a part of the radiant flow-in would be absorbed,
so,
 (  ), defined in Equation (10), must be equated with
the sum of the absorption coefficients of all individual
components, i.e.,


j
j


  

,
and, for the radiant flow-out,
 
exp j
j
II  

 




. (16)
As it is known, an integrated intensity equals the area
S(  ) under the curve of the corresponding intensity dis-
tribution function. Figure 3 shows, experimentally, the
re-absorption contours of the two components of inves-
tigated HeI ( = 5875Å). Then, assuming that I'(  ) cor-
responding to the sum intensities for the three compo-
nents distorted as a result of re-absorption during one
multiple passage is proportional to its corresponding area
S'(  ), and also S''(  ) corresponding to I'' (  ), the defini-
tion of the complete absorption coefficient [Equation (9)],
may be given as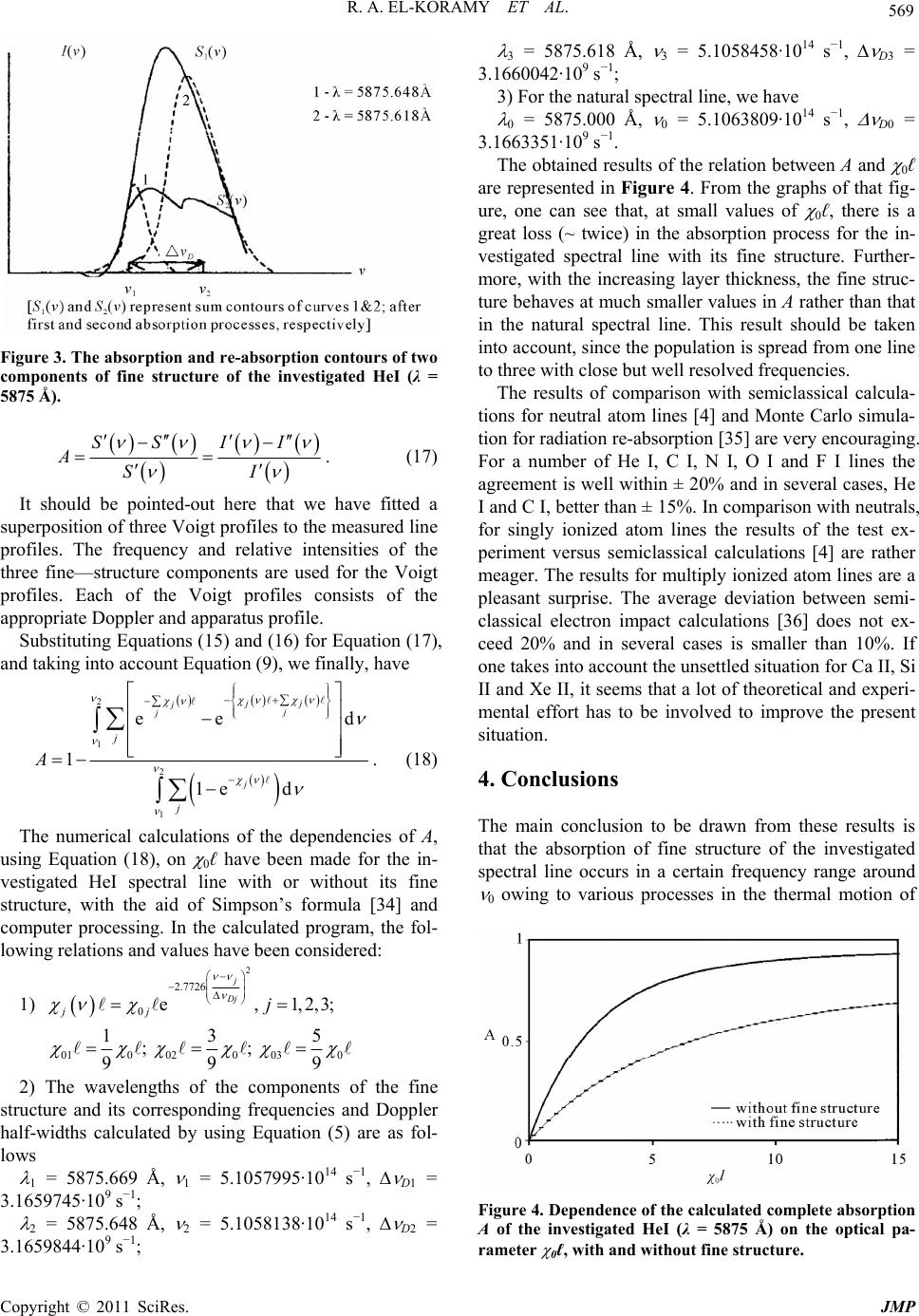

R. A. EL-KORAMY ET AL.
569
Figure 3. The absor ption and re-absorption co ntours of two
components of fine structure of the investigated HeI (λ =
5875 Å).
 





SS II
ASI



 





. (17)
It should be pointed-out here that we have fitted a
superposition of three Voigt profiles to the measured line
profiles. The frequency and relative intensities of the
three fine—structure components are used for the Voigt
profiles. Each of the Voigt profiles consists of the
appropriate Doppler and apparatus profile.
Substituting Equations (15) and (16) for Equation (17),
and taking into account Equation (9), we finally, have
  


2
1
2
1
ee
1
1e d
jj
jj
j
j
j
j
A





d






























. (18)
The numerical calculations of the dependencies of A,
using Equation (18), on 
0ℓ have been made for the in-
vestigated HeI spectral line with or without its fine
structure, with the aid of Simpson’s formula [34] and
computer processing. In the calculated program, the fol-
lowing relations and values have been considered:
1)

2
2.7726
0e, 1
j
Dj
jj j


 
 
 


 ,2,3;
010 020 030
13
; ;
99
5
9


2) The wavelengths of the components of the fine
structure and its corresponding frequencies and Doppler
half-widths calculated by using Equation (5) are as fol-
lows

1 = 5875.669 Å,

1 = 5.1057995·1014 s
−1, 

D1 =
3.1659745·10 9 s−1;

2 = 5875.648 Å,

2 = 5.1058138·1014 s
−1, 

D2 =
3.1659844·109 s−1;

3 = 5875.618 Å,

3 = 5.1058458·1014 s
−1, 

D3 =
3.1660042·109 s−1;
3) For the natural spectral line, we have

0 = 5875.000 Å,

0 = 5.1063809·1014 s
−1,

D0 =
3.1663351·109 s−1.
The obtained results of the relation between A and 
0ℓ
are represented in Figure 4. From the graphs of that fig-
ure, one can see that, at small values of

0ℓ, there is a
great loss (~ twice) in the absorption process for the in-
vestigated spectral line with its fine structure. Further-
more, with the increasing layer thickness, the fine struc-
ture behaves at much smaller values in A rather than that
in the natural spectral line. This result should be taken
into account, since the population is spread from one line
to three with close but well resolved frequencies.
The results of comparison with semiclassical calcula-
tions for neutral atom lines [4] and Monte Carlo simula-
tion for radiation re-absorption [35] are very encouraging.
For a number of He I, C I, N I, O I and F I lines the
agreement is well within ± 20% and in several cases, He
I and C I, better than ± 15%. In comparison with neutrals,
for singly ionized atom lines the results of the test ex-
periment versus semiclassical calculations [4] are rather
meager. The results for multiply ionized atom lines are a
pleasant surprise. The average deviation between semi-
classical electron impact calculations [36] does not ex-
ceed 20% and in several cases is smaller than 10%. If
one takes into account the unsettled situation for Ca II, Si
II and Xe II, it seems that a lot of theoretical and experi-
mental effort has to be involved to improve the present
situation.
4. Conclusions
The main conclusion to be drawn from these results is
that the absorption of fine structure of the investigated
spectral line occurs in a certain frequency range around

0 owing to various processes in the thermal motion of
Figure 4. Dependence of the calculated complete absorption
A of the investigated HeI (λ = 5875 Å) on the optical pa-
rameter 
0ℓ, with and without fine structure.

570 R. A. EL-KORAMY ET AL.
the gas atoms. Apart from its intrinsic interest in the
study of Doppler broadening, the phenomenon described
essentially in this review is important in connection with
the limitation of the resolution close spectral lines. This
limitation arises in a two-fold manner; the absorption is
reduced, making the lines more difficult to observe, but
this reduction is much less at the edge of a line than in
the center.
Another specific conclusion is that multiplets are very
useful in the assessment of the optical depth. The inten-
sity ratio of their components usually is well known for
the free atoms and ions, and any deviation will indicate
the magnitude of the self-absorption, the strongest com-
ponent being affected. Within limits the optical depths of
the individual components can even be derived.
The results of the present work predict that, if plasma
is seeded with atomic species having high absorption
coefficients for ground states atoms or ions, the respec-
tive resonance transitions easily become optically thick
and their spectral radiance allows a temperature meas-
urement. With respect to applications, these plasmas can
be used thus as high-power sources radiating at the
blackbody radiance in narrow spectral regions [37].
Furthermore, the results of this work support the as-
sumption made in its theoretical analysis that the line
broadening due to Doppler effects varies directly the
absorbed layer thickness. So, it is more convenient in an
experimental work of plasma laboratory to make the ab-
sorbent layer thickness as small as possible to avoid the
greater loss in the emitted radiation. On the other hand, it
is pointed out here that Doppler broadening calculations
have made possible a different and very convenient ap-
proach for determining the electron densities in dense
plasmas with an accuracy comparable to other spectro-
scopic methods [38].
Finally, the theoretical results of the calculations offer
a satisfactory agreement with the experimental data in
literature [20]. To extend the study to other ions of the
sequence, plasmas with known density and temperature
especially at higher values and/or spectrometers with
higher resolution are necessary.
5. Acknowledgements
The authors wish to express his gratitude to Prof. Dr.
Salama A. A, Professor of Numerical Analysis at Assiut
University, Assiut, Egypt for his guidance and valuable
assistance in the statistical calculations.
6. References
[1] H. R. Griem, M. Baranger, A. C. Kolb and G. Oertel,
“Stark Broadening of Neutral Helium Lines in a Plasma,”
Physical Review, Vol. 125, No. 1, 1962, pp. 177-195.
doi:10.1103/PhysRev.125.177
[2] H. R. Griem, “Stark Broadening of Isolated Spectral
Lines from Heavy Elements in a Plasma,” Physical Re-
view, Vol. 128, No. 2, 1965, pp. 515-523.
doi:10.1103/PhysRev.128.515
[3] W. Lochte-Holtgreven, “Plasma Diagnistics,” North-
Holland Company, Amsterdam, 1968.
[4] H. R. Griem, “Spectral Line Broadening by Plasmas,”
Academic Press, Inc., New York, 1974.
[5] A. N. Rubin and M. V. Belokon, “Influence of the Con-
centration of the Absorbent on the Depth of a Dip in
Stimulated Emission Spectrum of a Dye Laser Used in
Measurement of Weak Absorption by the Intracavity
Spectroscopy Method,” Soviet Journal of Quantum Elec-
tronics, Vol. 6, No. 1, 1976, pp. 79-81.
doi:10.1070/QE1976v006n01ABEH010823
[6] H. Bachau, F. Martin, A. Martin, A. Riera and M. Yanez,
“Resonance Parameters and Properties of Helium-Like
Doubly Excited States 2 ≤ z ≤ 10,” Atomic Data and Nu-
clear Data Tables, Vol. 48, No. 2, 1991, pp. 167-212.
doi:10.1016/0092-640X(91)90006-P
[7] N. Konjevic, “Plasma Broadening and Shifting of
Non-Hydrogenic Spectral Lines: Present States and Ap-
plications,” Physics Reports, Vol. 316, No. 6, 1999, pp.
339-401. doi:10.1016/S0370-1573(98)00132-X
[8] G. Torsi, E. Desimoni, F. Palmisano and L. Sabbatini,
“Determination of Lead in Air by Electro-Thermal
Atomic Spectroscopy with Electrostatic Accumulation
Furnance”, Analytical Chemistry, Vol. 53, No. 7, 1981,
pp. 1035-1038. doi:10.1021/ac00230a026
[9] S. G. Harris, “Intracavity Laser Spectroscopy: An Old
Field with New Prospects for Combustion Diagnostics,”
Applied Optics, Vol. 23, No. 9, 1984, pp. 1311-1318.
doi:10.1364/AO.23.001311
[10] A. P. Voitovich, A. Ch. Voitovich and V. V. Mashko,
“Resonance Polarization Phenomena in Broadband La-
sers with Anisotropic Absorbing Gas Media,” Laser
Physics, Vol. 5, No. 5, 1995, pp. 927-951.
[11] V. M. Baev, T. Latz and P. E. Toschek, “Laser Intracav-
ity Absorption Spectroscopy,” Applied Physics B, Vol. 69,
No. 3, 1999, pp. 171-202.
doi:10.1007/s003400050793
[12] J. Workman Jr. and A. W. Springsteen, “Applied Spec-
troscopy,” Academic Press, New York, 1998.
[13] V. S. Burakov and S. N. J. Raikov, “Intracavity Laser
Spectroscopy: Plasma Diagnostics and Spectral Analy-
sis,” Journal of Applied Spectroscopy, Vol. 69, No. 4,
2002, pp. 492-518. doi:10.1023/A:1020639728912
[14] Y. Toyozawa, “Optical Absorption and Reflectance,”
Encyclopedia of Condensed. Matter Physics, 2005, pp.
142-147.
[15] K. Shin, O. Noriyastu, T. Shuichi and N. Tomohide,
“Comparison of He I Line Intensit Ratio Method and
Electrostatic Probe for Electron Density and Temperature
Measurements in NAGDIS-II,” Physics of Plasmas, Vol.
13, No. 1, 2006, p. 13301.
[16] J.-W. Ahn, D. Craig, G. Flksel, D. J. Den Hartag and J. K.

R. A. EL-KORAMY ET AL.
571
Anderson, “Emission Intensities and Line Ratios from a
Fast Neutral Helium Beam,” Physics of Plasmas, Vol. 14,
No. 8, 2007, p. 3301 (10 pages).
[17] J. L. McHale, “Molecular Spectroscopy,” Prentice Hall,
Englewood Cliffs, 1998.
[18] Y. Toshimitsu, M. Norio, S. H. Ryugo, W. Eberhard and
E. John, “Antiprotonic Helium,” Physics Reports, Vol.
366, No. 4-5, 2002, pp. 183-187.
doi:10.1016/S0370-1573(01)00082-5
[19] J. M. Hollas, “Modern Spectroscopy,” 4th Edition, Jon
Wiley & Sons, New York, 2004.
[20] V. V. Grishachev, V. I. Denisov, V. G. Zhotikov, V. N.
Kuryatov and E. F. Nasedkin, “New Potentialities of In-
tracavity Spectroscopy of Matter Using Counterpropa-
gating Wave in a Ring Laser,” Opitics and Spectroscopy:
Physical and Quantum Optics, Vol. 98, No. 1, 2005, pp.
47-52.
[21] V. I. Denisov, V. V. Grishachev, V. N. Kuryatov, E. F.
Nasedkin and V. G. Zhotikov, “The Ultra-High Resolu-
tion Sensitivity by Spectral Measurement on the Basis of
Laser,” Journal of Quantitative Spectroscopy & Radia-
tion Transfers, Vol. 103, No. 2, 2007, pp. 302-313.
doi:10.1016/j.jqsrt.2006.02.057
[22] C. S. Matthew, J. T. Michael, A. Pe’er, J. Ye, E. S. Jason,
G. Vladislav and A. D. Scott, “Direct Frequency Comb
Spectroscopy,” Advances in Atomic, Molecular, and Op-
tical Physics, Vol. 55, 2008, pp. 1-60.
doi:10.1016/S1049-250X(07)55001-9
[23] S. Djenize, “Stark Broadening in the Sb III Spectrum,”
Physics Letters A, Vol. 372, No. 44, 2008, pp. 6658-
6660.
[24] S. I. Themelis, “Resonance Energies and Auto-Ionization
Widths 2p2 1De, 3d2 1Ge and 4f2 1Ie Doubly Excited States
of the Helium Iso-electric Sequence,” Physics Letters A,
Vol. 374, No. 44, 2010, pp. 4512-4516.
doi:10.1016/j.physleta.2010.09.021
[25] E. A. Sviridenkovinitsa (Ed.) “Intracavity Laser Spec-
troscopy,” Proceedings of SPIE, 1998.
[26] R. A. El-Koramy, “Transversal Magnetic Field Effect on
the Populations of Excited States of Helium Atoms in
Nanosecond Discharge,” International Journal of Mod-
ern Physics B, Vol. 18, No. 3, 2004, pp. 395-408.
doi:10.1142/S0217979204018503
[27] R. Deloche, P. Monchicourt, M. Cheret and F. Lambert,
“High-Pressure Helium after Glow at Room Tempera-
ture,” Physical Review A, Vol. 13, No. 3, 1976, pp. 1140-
1176. doi:10.1103/PhysRevA.13.1140
[28] N. A. Ashurbecov, V. S. Kurbanismailov, O. A. Omarov
and N. O. Omarova, “The Kinetics of Excited Atoms and
Optical Radiation under Conditions of Wave Mechanism
of Breakdown in Inert Gases,” High Temperature, Vol.
38, No. 5, 2000, pp. 795-810.
doi:10.1007/BF02755936
[29] J.-C. Gauthler, F. Devos and J. F. Delpech, “Temperature
Dependence of the Collisional Relaxation Processes for
the n=3 Triplet States of Helium,” Physical Review A,
Vol. 14, No. 6, 1976, pp. 2182-2189.
doi:10.1103/PhysRevA.14.2182
[30] J. E. Lawler, J. W. Parker, L. W. Anderson and W. A.
Fitzsimmons, “Helium 3 3S Decay Rates in a High-Pres-
sure after Glow,” Physical Review A, Vol. 19, No. 1 1979,
pp. 156-159.
[31] J. E. Lawler, J. W. Parker, L. W. Anderson and W. A.
Fitzsimmons, “Nanosecond Time-Resolved Spectroscopy
of the n = 2 Levels in a High-Pressure He Discharge,”
Physical Review Letters, Vol. 39, No. 9, 1977, pp. 543-
546. doi:10.1103/PhysRevLett.39.543
[32] S. Kubota, C. Davies and T. A. King, “Relaxation of He
(31S, 33S, 33P) States in Ne, Ar, Kr and Xe Collisions,”
Journal of Physics B: Atomic, Molecular and Optical
Physics, Vol. 8, No. 8, 1975, pp. 1220-1227.
[33] S. E. Frish, “Spektroskopiya Gazorazeryadnoi Plasmy,”
(Spectroscopy of Gas-Discharge Plasma), Nauka, Mos-
cow, 1970.
[34] N. C. Bakhvalov, “Numerical Methods,” Nauka, Moscow,
1973.
[35] M. Seo, M. Nimura, M. Hasuo and T. Fujimoto, “Dis-
alignment of Excited Atoms by Radiation Reabsorption:
Neon 2p2 Atoms in a Discharge Plasma,” Journal of
Physics B, Vol. 36, No. 9, 2003, pp. 1869-1884.
doi:10.1088/0953-4075/36/9/316
[36] M. S. Dimitrijevi, “A Program to Provide Stark-Broad-
ening Data for Stellar and Laboratory Plasma,” Journal of
Applied Spectroscopy, Vol. 63, No. 5, 1996, pp. 684-689.
doi:10.1007/BF02606861
[37] F. Bottcher, U. Ackermann and H.-J. Kunze, “Gas-Linear
Pinch as a Source of Blackbody—Limited VUV Line
Radiation”, Applied Optics, Vol. 25, No. 18, 1986, pp.
3307-3311. doi:10.1364/AO.25.003307
[38] K. H. Finken, G. Bertschinge, S. Maurmann., H.-J. Kunze,
“Spectroscopic Investigation of High-Density Plasmas
Produced in a z-Pinch,” Journal of Quantitative Spec-
troscopy and Radiation Transfers, Vol. 20, No, 5, 1978,
pp. 467-476. doi:10.1016/0022-4073(78)90050-X