 Intelligent Control and Automation, 2015, 6, 147-157 Published Online May 2015 in SciRes. http://www.scirp.org/journal/ica http://dx.doi.org/10.4236/ica.2015.62015 How to cite this paper: Al-Shabi, M. (2015) Simulation and Implementation of Real-Time Vision-Based Control System for 2-DoF Robotic Arm Using PID with Hardware-in-the-Loop. Intelligent Control and Automation, 6, 147-157. http://dx.doi.org/10.4236/ica.2015.62015 Simulation and Implementation of Real-Time Vision-Based Control System for 2-DoF Robotic Arm Using PID with Hardware-in-the-Loop Mohammad Al-Shabi Department of Mechatronics Engineering, Philadelphia University, Philadelphia, USA Email: mshabi@philad elphia.edu.jo Received 1 March 2015; accepted 23 May 2015; published 26 May 2015 Copyright © 2015 by author and Scientific Research Publishing Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). http://creativecommons.org/licenses/by/4.0/ Abstract Microsoft Kinect sensor has shown the research community that it's more than just an interactive gaming device, due to its multi-functional abilities and high reliability. In this work, online HIL (Hardware-in-the-Loop) experimental data are used to apply human motion imitation to a 2-degree of freedom Lego Mind storm NXT robotic arm. A model simulation of the dc motor used in this ex- periment is also present in this paper. The acquired input data from the Kinect sensor are processed in a closed loop PID controller with feedback from motors encoders. The applied algo- rithms solve the overlapping input problem, conducting a simultaneous control of both shoulder and elbow joints, and solving the overlapping input problem as well. The work in this paper is presented as a prototype to assure the applicability of the algorithms, for further development. Keywords HIL, NXT, Kinect, PID, Real-Time, Image Processing, Imitation, 2-DoF 1. Introduction Three-dimensional data recognition and processing are recently a vital research area for many modern applica- tions in Mechatronic and the field of engineering in general. Kinect, which is a motion detection and recognition smart sensor developed by the engineers at Microsoft, allows human/computer interaction needless to any phys- ical controllers. The sensor contains two cameras for image acquisition, an RGB camera that captures colors and  M. Al-Shabi a laser camera that captures depth [1]. The processor inside the Kinect recognizes human movement patterns to generate a corresponding skeleton model that can be provided in a computer environment such as Matlab [2]-[8]. The data provided by the Kinect have opened the door to develop new methods and algorithms. A comparison between different methodologies to determine the patterns provided by the Kinect was discussed in [9]. Simula- tions and real-life implementations were presented to validate which method resulted less errors. HGR (Hand- Gesture Recognition) system was presented in [2] [10], where the system recognized the user’s hands and fin- gers to translate their movement patterns into sign language. The system used skin color matching algorithms along with HMM (Hidden Markov Models) for training and continuous-motion tracking. Studying and analyzing gait abnormalities are essential in neurological examinations of walking disorders. The work in [11] provided analysis on the effects of Parkinson’s disease on the deviations in human walking. Two sets of data were used in this experiment. The first one was comprised of walking patterns of healthy people, where the second contained patterns of patients with walking disorders. The abnormalities were found and classified by comparing the differences in motion detected between the two sets of data. In [12], Kinect was used to control the mobility of a wheeled Lego Mindstorm robot through Matlab. In order to monitor the robots environment, a mobile phone was mounted on the robot to utilize its camera as feedback to the user. The system recognized the user’s hand-gestures that were captured by the Kinect sensor. The algorithm translated those gestures into predefined commands, to be processed and sent over to the robot [13]-[15]. In this work, an algorithm is developed to extract the angles from the detected skeleton model by the Kinect sensor. Only two of the angles are then sent to the NXT robot to control two linked servo motors representing the shoulder and the elbow joints. 2. Mathematical Model This section describes the mathematical model of the plant, and is divided into two parts: - The first part describes the transf er fun ctions of the servo motors while; - The second part dwells into the details of the robots s tatic/dynamic stability and CG (Center of Gravity). The servo dc motors torque is proportionally related to its curr ent through its constant as shown in Equation (1) [16]. The relation between that current and the voltage applied to the motor is explained through KVL (Kerchoff Voltage Law) in Equation (2) for the dc motor structure in Figure 1. (1) a RLbaa DI VVVVIRL Dt =++= + (2) Combining Equations (1) and (2) then taking the Laplace transformation to obtain: e a m aa a K L T VR SL = + (3) Figure 1. dc motor structure [16].  M. Al-Shabi Considering friction and motor load in Equation (4) then substituting its Laplace transform in (3), to obtain the relation between the angular velocity and torque in (5). (4) ( ) ( ) 1 m sJ b Ts SJ ω = + (5) Substituting Equation s (4) in (3) gives the relation between the armature voltage and the angular speed of the motor in Equation (6). ( ) ( ) e a aa a K LJ s Vs R b SS JL ω = ++ (6) Divide both sides by to obtain the transfer function in terms of voltage to position in Equation (7). ( ) ( ) e K LJ s Vs R b SS S JL α αα α Θ = ++ (7) is the angular position of the motor in rad. is the angular velocity of the motor in rad/sec. Va is the armature voltage in volts. Ke is the torque constant in N⋅m/A. is the motor viscous friction constant in N⋅m⋅s. La is the field inductance in H. Ra is the field resistance in Ohms. J is moment of inertia in kg⋅m2. Finally, the motor’s model is ready for simulation after substituting values from Table 1 for the constants in the transfer function in Equation (8). () () ( ) 6 3 6 0.47 0.153.228 10 1.13 106.9 0.15 3.228 10 a s Vs SS S − − − ×× Θ = × ++ × (8) Table 1. NXT servo motor parameters [17]. Parameter Value and unit Ke 0.47 N⋅m/A B 1.13 × 10−3 N⋅m⋅s La 0.15 H Ra 6.9 Ohms J 3.228 × 10−6 kg⋅m2  M. Al-Shabi 3. Simulation and Preliminary Results The proposed algorithm is summarized in Figure 2. The Kinect sensor is used as an image acquisition input for the algorithm’s Matlab Simulink as shown in Figure 3. The acquired skeleton is then viewed as shown in Fig- ure 4, and the angle of the elbow is extracted. The data is processed through the created Simulink and sent to the transfer function of the motor in Figure 5. The sampling time for the acquired data in the simulation is 0.033 seconds to match the number of frames captured by the Kinect per second. Changing the reference angle of the elbow joint manually by the user, caused the responses of the motor to be jerky and unstable, thus PID control method as in Figure 6 and Figure 7, is used in this simulation to enhance and smooth the motor’s response. The simulation results for the modeled motor shows the response of the motor's angle compared to the user's input as shown in Figure 8. The PID algorithm applied is resulting smooth responses to the minor changes in the users elbow angle, eleminating the jerky movement and sucsessfully overcoming the over-lapping input changes. A delay of approximately 1 second is noticed in the simulation results, which is left to deal with later on in the hardware implementation in Section 3. Figure 2. Flow chart of the system. Figure 3. Kinect Simulink library based on [12] [18].  M. Al-Shabi Figure 4. Depth view of the skeleton data showing the elbow angle. Figure 5. Simulink created for the system. Figure 6. Th e system’s loop. 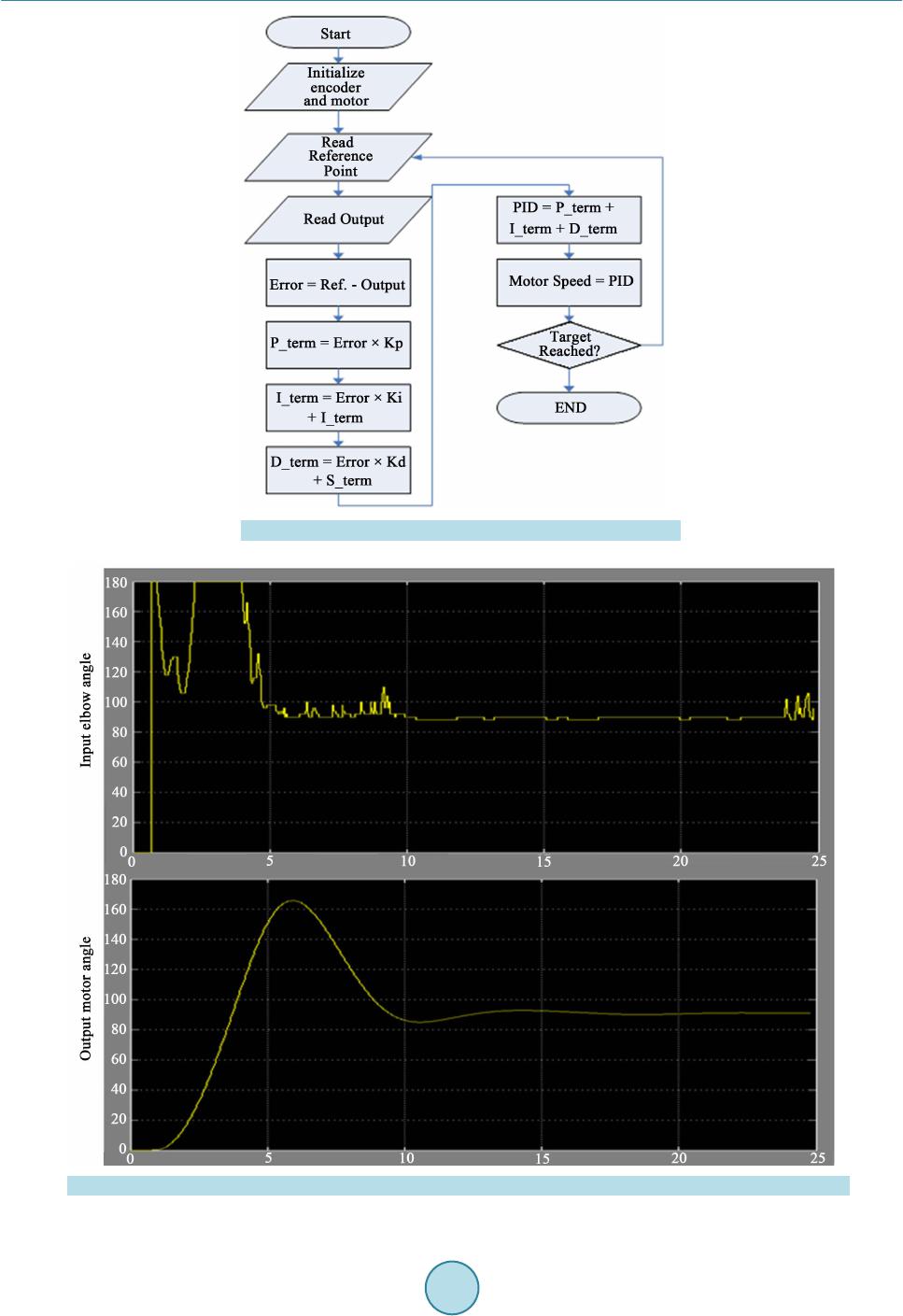 M. Al-Shabi Figure 7. PID algorithm flowchart. Figure 8. Elbow angle input and output motor response. 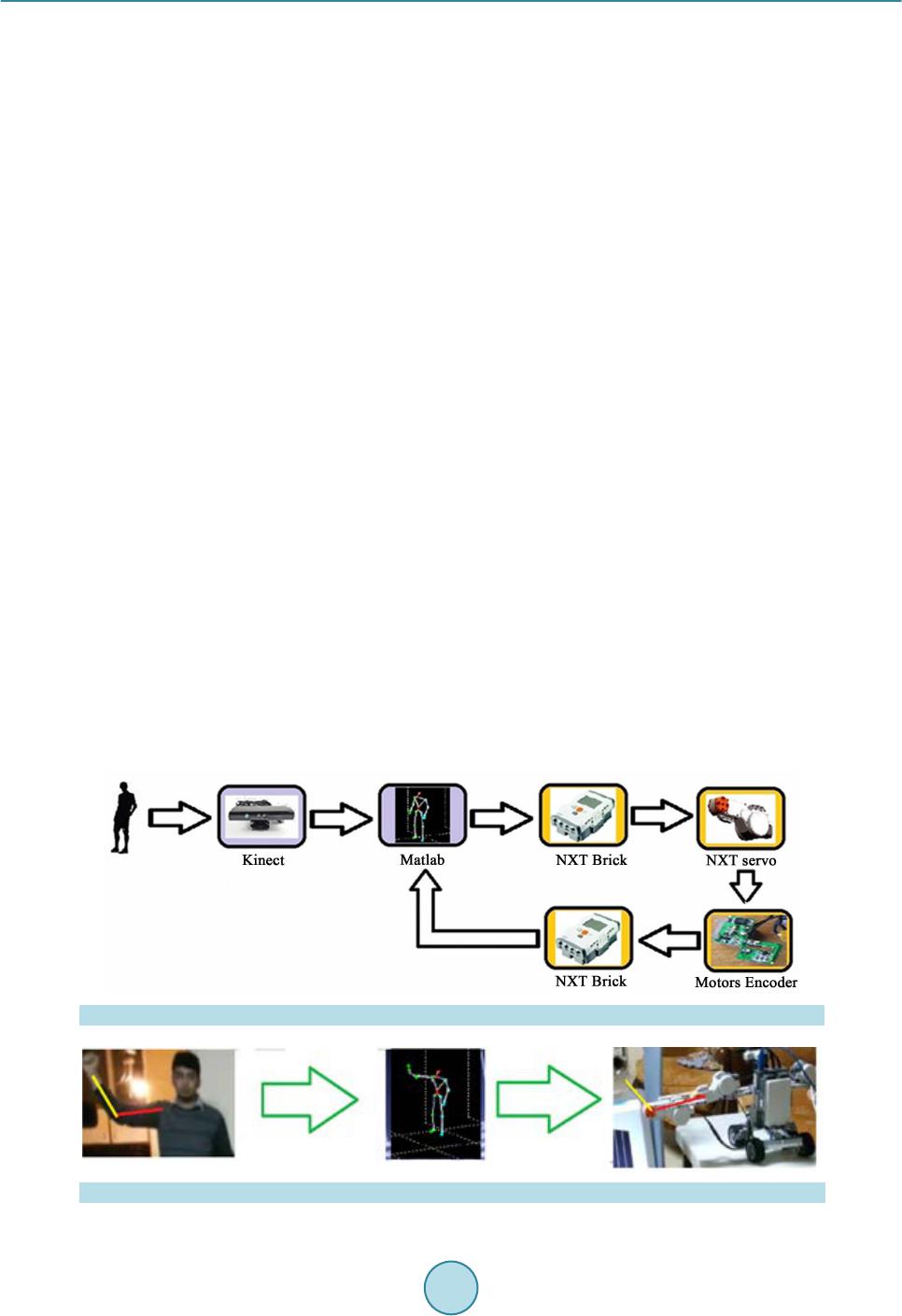 M. Al-Shabi 4. 2-Dof Hardware in the Loop The system simply consists of the Kinect sensor, an NXT Lego Mindstorm brick two NXT dc servo motors a computer. The Kinect sensor is connected to the computer, and Matlab works as a host environment for the Ki- nect to process the skeleton data. The data is processed and sent online to the NXT brick, which only bypasses the data and works as a drive for the NXT motors. The encoders mounted on the motors send the feedback data to the NXT brick which sends it back to Matlab, Figure 9. The 1st motor is mounted on the NXT brick representing the shoulder joint, while the 2nd one is mounted at the end of the 1st one, representing the elbow joint. The distance between the shoulder motor and the elbow mo- tor is the arm link. On the shaft of the 2nd motor, a plastic rod is mounted to represent the elbow link, as shown in Figure 10. The sampling time for the NXT brick was chosen to be 0.02 seconds, which is the minimum time that the brick can handle for processing the data. This results of an outstanding reduction in the response delay which can be noticed in both motors for position and speed responses. Even though both motors are identical, different PID values are implemented for each motor, due to differences in the resultant forces and torques ap- plied on each one. 5. Results and Analysis Results for both motors representing shoulder and elbow joints are described in this section. For all simulations, a sampling time of 0.02 is used. A comparison between input angles and motors angles are described and ana- lyzed for the 2-DoF arm. Angular velocities are studied to understand the limitations of the motors. The system is able to respond quickly, and shows good stability to varying inputs with accurate positioning and low over- shoot. In terms of angles changing over time, the responses of the shoulder and elbow motors to their inputs are shown in Figure 11 and Figure 12, respectively. Samples of the data were taken and represented in Figure 13 and Figure 14. The selected data shows that for the shoulder motor, a maximum over shoot of eight degrees is noticed with 0.33 seconds settling time. Analyzing the angular velocities of the shoulder motor in Figure 15 and the elbow motor in Figure 16, shows that both are able to match the rate of change of the human arm angles to certain limit-due to the motors physical limitation. Yet, the system manages good stability during sudden changes in speed and direction. 6. Conclusions The results show that the system is robust and accurate for controlling position. On the other hand, the system faced limitations for high angular velocity inputs due to the physical limitations of the motors. This problem can be easily overcome by selecting motors with higher maximum speed and few adjustments to the algorithm used. Figure 9. Block diagram of the system. Figure 10. Practical sequence of operation.  M. Al-Shabi Figure 11. Shoulder input angle vs corresponding motor angle. Figure 12. Elbow input angle vs corresponding motor angle. Figure 13. Data section for shoulder motor response.  M. Al-Shabi Figure 14. Data section for elbow motor response. Figure 15. Shoulders angular velocity (input ) and the motors angular velocity (output).  M. Al-Shabi Figure 16. Elbow angular velocity (input) and the motors angular velocity (output). The elbow motor showed better response in terms of overshoot and settling time because of its load lower than the shoulder motor that carried that elbow motor. Acknowledgements The author of this paper would like to thank the Mechatronics department in Philadelphia University for their support and providing the required apparatus and equipment for this project. Special thanks for Iyad Sawalmeh and Samer Al-Shaer for their help through this project. References [1] Microsoft (2009) Project Natal. [2] Li, Y. (2012) Multi-Scenario Gesture Recognition Using Kinect. The 17th International Conference on Computer Games, Louisville, 30 July-August 1 2012, 126-130. http://dx.doi.org/10.1109/cgames.2012.6314563 [3] Machida, E., Cao, M., Murao, T. and Hashimoto, H. (2012) Human Motion Tracking of Mobile Robot with Kinect 3D Sensor. 2012 Proceedings of SICE Annual Conference, Akita, 20-23 August 2012, 2207-2211. [4] Wang, Y., Yang, C., Wu, X., Xu, S. and Li, H. (2012) Kinect Based Dynamic Hand Gesture Recognition Algorithm Research. The 4th International Conference on Intelligent Human-Machine Systems and Cybernetics, Nanchang, 26-27 August 2012, 2 74-279. http://dx.doi.org/10.1109/ihmsc.2012.76 [5] Zhang, C., Xu, J., Xi, N., Jia, Y. and Li, W. (2012) Development of an Omni-Directional 3D Camera for Robot Navi-  M. Al-Shabi gation. The 2012 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Taiwan, 11-14 July 2012, 262-267. http://dx.doi.org/10.1109/AIM.2012.6266033 [6] Procházka, A., Vyšata, O., Valis, M. and Yadollahi, R. (2013) The MS Kinect Use for 3d Modelling and Gait Analysis in the Matlab Environment. Technical Computing 2013, Prague. [7] Li, B. (2013) Using Kinect for Face Recognition under Varying Poses, Expressions, Illumination and Disguise. Appli- cations of Computer Vision (WACV), Tampa, 15-17 January 2013, 186-192. http://dx.doi.org/10.1109/wacv.2013.6475017 [8] Prochazka, A., Kubicek, M. and Pavelka, A. (2006) Multicamera Systems in the Moving Body Recognition. 48th In- ternational Symposium ELMAR-2006 Focused on Multimedia Signal Processing and Communications, Zadar, June 2006, 45-48. http://dx.doi.org/10.1109/elmar.2006.329511 [9] Staranowicz, A. and Mariottini, G.-L. (2013) A Comparative Study of Calibration Methods for Kinect-Style Cameras. University of Texas at Arlington, Arlington. [10] Li, Y. (2012) Hand Gesture Recongnition Using Kinect. University of Louisville, Louisville. [11] Harrison, T.R. (2011) Chapter 367: Approach to the Patient with Neurologic Disease. In: Longo, D.L., Fauci, A.S., Kasper, D.L., Hauser, S.L., Jameson, J.L. and Loscalzo, J., Eds., Harrison’s Principles of Internal Medicine, McGraw Hill Professional, New York. [12] Ivanescu, L. (2014) KEV3. http://www.mathworks.com/matlabcentral/fileexchange/47968-kev3 [13] Lasenby, J. and Stevenson, A. (2001) Using Geometric Algebra for Optical Motion Capture. Birkhäuser, Boston. http://dx.doi.org/10.1007/978-1-4612-0159-5_8 [14] Ringer, M. and Lasenby, J. (2002) Multiple Hypothesis Tracking for Automatic Optical Motion Capture. Lecture Notes in Computer Science, 2350, 524-536. [15] http://www.hi.jpl.nasa.gov/projects/ [16] Dorf, R.C. and Bishop, R.H. (2001) Modern Control Systems. 9th Edition, Prentice-Hall, Englewood Cliff. [17] Watanabe, R. (2015) NXT Motor Parameters. http://wayback.archive.org/web/20111010092210/ http://web.mac.com/ryo_watanabe/iWeb/Ryo%27s%20Holiday/NXT%20Motor.html [18] Kroon, D.-J. (2011) Mathworks. http://www.mathworks.com/matlabcentral/fileexchange/30242-kinec t-matlab
|