Journal of Computer and Communications
Vol.03 No.05(2015), Article ID:56619,7 pages
10.4236/jcc.2015.35023
Image Registration Technique Based on a Fast CPD Algorithm
Wei Guang Liu, Tian Wang
School of Computer, Zhongyuan University of Technology, Zhengzhou, China
Email: wtxhlu1989@163.com


Received April 2015

ABSTRACT
The Coherent Point Drift (CPD) algorithm which based on Gauss Mixture Model is a robust point set registration algorithm. However, the selection of robustness weight which used to describe the noise may directly affect the point set registration efficiency. For resolving the problem, this paper presents a CPD registration algorithm which based on distance threshold constraint. Before the point set registration, the inaccurate template point set by resampling become the initial point set of point set matching, in order to eliminate some points that the distance to target point set is too close and too far in the inaccurate template point set, and set the weights of robustness as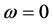 . In the simulation experiments, we make two group experiments: the first group is the registration of the inaccurate template point set and the accurate target point set, while the second group is the registration of the accurate template point set and the accurate target point set. The results of comparison show that our method can solve the problem of selection for the weight. And it improves the speed and precision of the original CPD registration.
. In the simulation experiments, we make two group experiments: the first group is the registration of the inaccurate template point set and the accurate target point set, while the second group is the registration of the accurate template point set and the accurate target point set. The results of comparison show that our method can solve the problem of selection for the weight. And it improves the speed and precision of the original CPD registration.
Keywords:
Point Set Registration, Coherent Point Drift, Distance Threshold Constraint, Gauss Mixture Model

1. Introduction
The point set registration technology is widely used in image registration, target recognition, computer vision, image retrieval and classification, the mobile robot and so on. The registration usually falls into two categories: rigid or non-rigid. The goal of point set registration is to find the corresponding relationship between two sets of points and to solve the transform relationship. However, two sets of points were obtained from different imaging equipment, different perspectives, different time or different conditions (weather, illumination), so the relationship between two sets of points is not sure, and also due to deformation, noise and outliers, the point set matching is a very difficult problem.
Currently, point set registration algorithm is roughly divided into two categories: the one is based on the transformation parameter estimation algorithm, such as Coherent Point Drift [1], the iterative closest point [2], based on thin plate spline point set registration (TPS-RPM) [3]; and another kind is based on the feature registration algorithm, such as based on the algorithm of shape context [4], based on invariant features (SIFT) [5], based on spectral graph theory [6] and so on. Iterative closest Point(ICP) algorithm [2] [7] can better solve the problem of rigid registration, is based on a closest distance criterion and finds corresponding points through continuous iteration to establish corresponding relationship between two sets of points, and to solve transformation model, then to redetermine the corresponding relationship, and until it reaches the local minimum. Its structure is simple, computational complexity is low, but it may be more sensitive for noise and outliers, requires that the initial position of the two point sets be adequately close. TPS-RPM [3] effectively solve the defect of ICP, not only applies to the rigid registration, also to the non-rigid, and has the very strong robustness. However this algorithm is easy to fall into local optimum, and the iteration speed slower. The algorithm based on the feature usually requires the size, location, neighborhood structure between the two point sets cannot vary widely.
Compared with other point set registration algorithms, CPD has higher registration precision, not only to the rigid registration, also to the non-rigid. However, it finds the corresponding relationship between the two point sets by EM iteration minimizing the expectation of the negative log-likelihood function, there are two major defects: the one is that the selection of the weight parameters which is used to account for the noise and outliers directly affects the precision and efficiency of registration. Another is that the selection of initial registration parameters has important influence to the whole, may be trapped in local optimal solution. For the problem, this paper simply introduces the process of original CPD algorithm, and then presents a CPD registration algorithm based on distance threshold constraint. Before the point set registration, the inaccurate template point set by resampling becomes the initial point set of point set matching, in order to eliminate some points that the distance to target point set is too close and too far in the inaccurate template point set. And the experiment proves that it can improve the speed and precision of the original CPD registration.
2. The Coherent Point Drift Algorithm
2.1. The Introduction of CPD Algorithm Principle [1]
In fact, the CPD can be seen as a kind of probability density parameter estimation problem, where one point set represents the Gaussian mixture model centroids, and the other one represents the data points, the problem changes into maximum likelihood estimation by establishing the logarithmic likelihood function of the data points, We define the correspondence probability between two points sets as the posterior probability of the GMM centroids given the data point, the optimal registration place is likely to be the largest posterior probability.
Set up two sets of points: we define the template point set as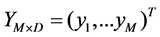 , and the target point set as
, and the target point set as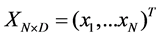 ,
, 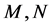 represent the number of points,
represent the number of points,  is the dimensions of the point set. We defines an uniform distribution as
is the dimensions of the point set. We defines an uniform distribution as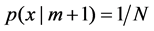 , the weight is
, the weight is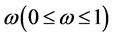 . And the probabilities
. And the probabilities 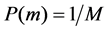 for all GMM components. So we get the weighted GMM probability density function [8]. And to see (1):
for all GMM components. So we get the weighted GMM probability density function [8]. And to see (1):
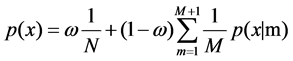 (1)
(1)
where . In registration process, when the template point set geome-
. In registration process, when the template point set geome-
try transformation,  is also changing. Through the covariance analysis, we consider that larger value of
is also changing. Through the covariance analysis, we consider that larger value of 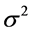 show that multiple points in the template point set corresponding to a point in the target point set. In order to find a one-to-one relationship,
show that multiple points in the template point set corresponding to a point in the target point set. In order to find a one-to-one relationship,  must be infinitely close to a minimum. So, we define geometric transformation relations of the template point set and the target point as
must be infinitely close to a minimum. So, we define geometric transformation relations of the template point set and the target point as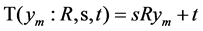 , where R is a rotation matrix, t is a translation vector and s is a scaling parameter. We define the registration parameter set as
, where R is a rotation matrix, t is a translation vector and s is a scaling parameter. We define the registration parameter set as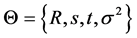 , and according to the maximization likelihood function method, the parameter values are then found by minimizing the expectation of the negative log-likelihood function in (2):
, and according to the maximization likelihood function method, the parameter values are then found by minimizing the expectation of the negative log-likelihood function in (2):
 (2)
(2)
CPD algorithm finds parameters 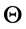 by Expectation Maximization (EM) iteration [9]. E-step: to estimate the initial parameters, and use the Bayes’ theorem to compute a posterior probability distributions of mixture components. Then the objective function Q is an upper bound of the negative log-likelihood function in (2). M-step: to update parameters by minimizing the objective function in (3).
by Expectation Maximization (EM) iteration [9]. E-step: to estimate the initial parameters, and use the Bayes’ theorem to compute a posterior probability distributions of mixture components. Then the objective function Q is an upper bound of the negative log-likelihood function in (2). M-step: to update parameters by minimizing the objective function in (3).

where

where
Although the EM [9] [10] iterative algorithm can converge to the minimum of the negative logarithm likelihood function, the selection of directly affect the precision and efficiency of the point set registration. So, this paper presents a CPD registration algorithm which based on distance threshold constraint, in order to eliminate some points that the distance to target point set is too close and too far in the inaccurate template point set. And set the weights of robustness as
2.2. The Improvement of CPD Algorithm
For the template point set Y and the target point set X, for a point 













We have found







Fist-step: For the template point set Y and the target point set X, we search for five points which ordered from small to large according to the distance of 





Second-step: As same as One-step, we search for five points which ordered from large to small according to the distance of 



Third-step: Firstly, we compute the average distance between the adjacent point of Point set X by Equation (5). Assume that the coordinates of the five points are






Fourth-step: Computing the coordinates 

where
Fifth-step: We get the distance threshold value interval of the target point set to the template point set. We weed out the noise points which are away from the template point set with

Sixth-step: If 






2.3. Experiment and Analysis
We use Windows XP system, Intel Pentium Dual, the memory of 1.81 GHz, 2 GB and the development environment is Matlab 2011b. We prepare Two groups of non-rigid images from different light, different perspective shooting as our experimental data. Converting the color images to the grayscale by Matlab, and extracting the image edge by canny method. In the process of extracting edges, in order to ensure the integrity and continuity of the image edge, there may be some noise points in extracted images. Figure 1(a) is shoot under the condition of the weak illumination change, after a series of operations, there is less noise in the extracted image. However, Figure 1(b) is shoot under the condition of the strong light change, there is more noise in the image edge. And the rotation, translation, scaling transformation will exist between the two images.
In order to verify the algorithm in this paper, Figure 1(a) is the inaccurate template point set, Figure 1(b) is the accurate target point set. Figure 2 show the process of registration between the inaccurate template point set and the accurate target point set with the original algorithm of CPD. We can see that CPD has very strong robustness for noise and outliers, eventually achieve a precise matching. But the number of iteration is as high as 117 times, 12 minutes 20.9318 seconds. If we make a precise processing for the inaccurate data before registration, on the basis of ensuring the integrity of the target edge character, we eliminate some noise points. The verification results are shown in Figure 3. Figure 3 show that after eliminating the noise points, the template point set quickly find the matching position, and the registration error is very small when the iteration times are 10 , always takes 2.6792 seconds and iteration 46 times. So the experiment proves that this algorithm can improve the speed and precision of the original CPD registration.
This experiment uses two critical condition of iteration as registration accuracy standard, namely covariance and standard tolerance. Refer to (8):

where


Figure 1. The simulation data. (a)The original image and edge image; (b) The original image and edge image.
Figure 2. The iterative process of the original CPD.
Figure 3. The iterative process of this algorithm registration.
time and the previous logarithmic likelihood function values.
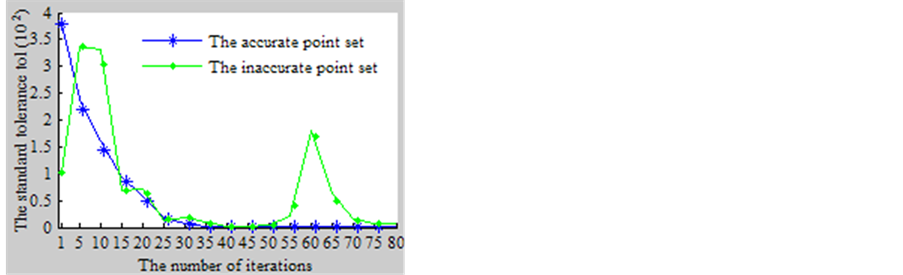
Figure 4 shows the comparison experiment on the registration accuracy between the inaccurate template point set and the accurate template point set. The X axis is the number of iterations. With the increase of the number of iterations, the changes on the covariance and standard tolerance. We can see that when we use the accurate template point set, curve is monotone decreasing, and soon reach a steady state. For inaccurate templates point set, due to the interference of noise, may cause relevant points registration errors or fall into local optimum, curve is not smooth, and achieve the speed of smaller registration error is slow.
In the Table 1, 




Figure 4. The comparison experiment on the registration accuracy between the inaccurate template point set and the accurate template point set.
Table 1. The comparison of output with this algorithm and the original CPD.
achieve a smaller value on the registration accuracy, this algorithm is better than the original algorithm on the accuracy.
4. Conclusion
The Coherent Point Drift is a kind of efficient point set registration algorithm, and obtains better effect, but the selection of robustness weight may directly affect the point set registration efficiency. So this paper presents a CPD registration algorithm which based on distance threshold constraint. The experiment proves that these point sets which resampling by this algorithm are involved in CPD registration algorithm, the weight of robustness is
Cite this paper
Wei Guang Liu,Tian Wang, (2015) Image Registration Technique Based on a Fast CPD Algorithm. Journal of Computer and Communications,03,182-188. doi: 10.4236/jcc.2015.35023
References
- 1. Myronenko, A. and Song, X.B. (2010) Point-Set Registration: Coherent Point Drift. IEEE Transactions on Pattern Analysis and Machine Intelligence, 32, 2262-2275. http://dx.doi.org/10.1109/TPAMI.2010.46
- 2. Dai, J.L., Chen, Z.Y. and Ye, X.X. (2007) The Application of ICP Algorithm for Point Cloud Registration. Journal of Image and Graphics, 12, 517-521.
- 3. Chui, H. and Rangarajan, A. (2003) A New Point Matching Algorithm for Non-Rigid Registration. Computer Vision and Image Understanding, 89, 114-141. http://dx.doi.org/10.1016/S1077-3142(03)00009-2
- 4. Belongie, S., Malik, J. and Puzicha, J. (2002) Shape Matching and Object Recognition Using Shape Contexts. IEEE Transactions on Pattern Analysis and Machine Intelligence, 24, 509-522. http://dx.doi.org/10.1109/34.993558
- 5. Gope, C. and Kehtarnavaz, N. (2007) Affine Invariant Comparison of Point-Sets Using Convex Hulls and Hausdorff Distances. Pattern Recognition, 40, 309-320.
- 6. Caetano, T.S., McAuley, J.J., Cheng, L., et al. (2009) Learning Graph Matching. IEEE Transactions on Pattern Analysis and Machine Intelligence, 31, 1048-1058. http://dx.doi.org/10.1109/TPAMI.2009.28
- 7. Xie, Z.X., Xu, S. and Li, X.Y. (2010) A High-Accuracy Method for Fine Registration of Overlapping Point Clouds. Image and Vision Computing, 28, 563-570. http://dx.doi.org/10.1016/j.imavis.2009.09.006
- 8. Jian, B. and Vemuri, B.C. (2011) Robust Point Set Registration Using Gaussian Mixture Models. IEEE Transactions on Pattern Analysis and Machine Intelligence, 33, 1633-1645. http://dx.doi.org/10.1109/TPAMI.2010.223
- 9. Luo, B. and Hancock, E.R. (2002) Iterative Procrustes Alignment with the EM Algorithm. Image and Vision Computing, 20, 377-396. http://dx.doi.org/10.1016/S0262-8856(02)00010-0
- 10. Myronenko, A. and Song, X.B. (2009) On the Closed-Form Solution of the Rotation Matrix Arising in Computer Vision Problems. Oregon Health and Science Univ., Tech. Rep. arXiv:0904.1613v1.
- 11. Xin, W. and Pu, J.X. (2011) Point Cloud Integration Based on Distances between Points and Their Neighborhood Centroids. Journal of Image and Graphics, 16, 886-891.
- 12. Zhong, Y. and Zhang, M. (2014) Automatic Registration Technology of Point Cloud Based on Improve ICP Algorithm. Control Engineering of China, 21, 112-121.