Received March 2015

ABSTRACT

Magnetotactic bacteria optimization algorithm (MBOA) is a new optimization algorithm inspired by the characteristics of magnetotactic bacteria, which is a kind of polyphyletic group of prokaryotes with the characteristics of magnetotaxis that make them orient and swim along geomagnetic field lines. The original Magnetotactic Bacteria Optimization Algorithm (MBOA) and several new variants of MBOA mimics the interaction energy between magnetosomes chains to obtain moments for solving problems. In this paper, Magnetotactic Bacteria Optimization Algorithm with the Best Individual-guided Differential Interaction Energy (MBOA-BIDE) is proposed. We improved interaction energy calculation by using the best individual-guided differential interaction energy formation. We focus on analyzing the performance of different parameters settings. The experiment results show that the proposed algorithm is sensitive to parameters settings on some functions.

Keywords:

Magnetotactic Bacteria, Nature Inspired Computing, Differential Interaction Energy, Parameters Settings

1. Introduction

The research of algorithms have been conducted many years, the field of algorithm is very mature now. Evolutionary algorithm (EA) is a very popular research field. The common evolutionary algorithms are genetic algorithm (GA), Differential Evolution (DE) [1], Particle Swarm Optimization (PSO) [2] and Bacterial Foraging Optimization algorithm (BFOA) [3] and so on.

Magnetotactic Bacteria Optimization Algorithm (MBOA) [4] [5] which is introduced by Mo is one of the modern heuristic algorithms and inspired by the magnetotactic bacteria. In nature, magnetotactic bacteria (MTBs) is a special kind of bacteria which have many micro magnetic particles named magnetosome in their bodies. These magnetic particles can generate moments to guide the bacteria to swim along geomagnetic field lines of the earth [6] [7]. In recent years, several improved MBOA, such as BMMBOA [8], MBOA-BR [9], MBOA-BT [10], PSMBA [11], MBMMA [12], have been proposed to modify the performance of MBOA. In the Moments of the Best Individual-based Magnetotactic Bacteria Optimization Algorithm (BMMBOA), similar to DE/best/1, the problem solutions are generated by moments mechanisms based on interaction energy among solutions [8]. In the Magnetotactic Bacteria Optimization Algorithm Based On Best-R and Scheme (MBOA-BR), similar to DE/best/r and scheme, it regulates the moments based on the information exchange between best individual's moments and some randomly one [9]. In the Magnetotactic Bacteria Optimization Algorithm based on Best-Target (MBOA-BT), similar to DE/best/target scheme, some cells will receive MTS information from the interaction between the local best one and the target one to balance the local search and global search [10]. In the Power Spectrum-Based Magnetotactic Bacteria Algorithm (PSMBA), it is based on the models of power spectra of the magnetic field noise produced by Brownian rotation of nonmotile bacteria in zero magnetic field [11]. In the Magnetotactic Bacteria Moment Migration Algorithm (MBMMA), the moments of relative good solutions can migrate each other to enhance the diversity of the MBMMA [12].

In this paper, we proposed a Magnetotactic Bacteria Optimization Algorithm with the Best Individual-guided Differential Interaction Energy (MBOA-BIDE) in order to overcome the shortcomings of complicated interaction energy calculation of the original MBOA and several new variants of MBOA and focus on the study of the effect of different parameters settings.

2. Magnetotactic Bacteria Optimization Algorithm with the Best Individual-Guided Differential Interaction Energy (MBOA-BIDE)

In the following, we briefly describe the basic operators and the main steps of MBOA-BIDE. MBOA-BIDE mainly has three steps and three main operators including moment generation, moment regulation, moment replacement.

2.1. Interaction Distance

First, in the algorithm, each solution is looked as a cell containing a magnetosome chain. At first we define stands for the best cell of the population in the current generation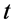. The distance of the cell and the

best cell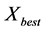, , 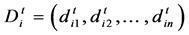is calculated as follows: .

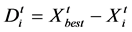(1)

After that, we can get a distance matrix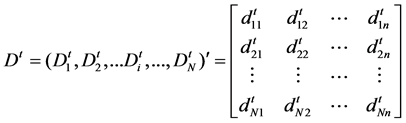. 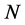is the size of cell population, 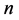stands for dimension of every cell.

2.2. Moments Generation

Based on the distances among cells, the interaction energy is defined as

(2)

where the settings of and will be discussed in the next section. 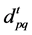stands for randomly selected variables from.,.

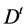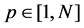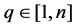After obtaining interaction energy, the moments are generated as follows:

(3)

where the settings of will be discussed in the next section.

Suppose, we can obtain a moment vector matrix.

Then the total moments of a cell is regulated as follows:

(4)

where stands for the moment of a randomly selected MTS from.,.

2.3. Moments Regulation

After moments generation, the moments regulation is realized as follows:

If > 0.5, the moments in the cell are regulated as follows:

(5)

Otherwise, they are regulated as follows:

(6)

where stands for the th dimension of current best cell in the current generation.

2.4. Moments Replacement

After the moments regulation, we set a replacement probability 0.5, some cells with worse fitness are replaced as follows:

if > 0.5,

(7)

where is a random number between 1 and. stands for the moment of a randomly selected MTS from

3. Parameters Settings

To evaluate the performance of MBOA-BIDE, the experiments are carried out on 10 benchmark functions. In this section, the benchmark functions are presented firstly. Secondly, the simulation results obtained from different parameter settings are analyzed and discussed.

In all experiments, during each run, a maximum fitness evaluation of 200000 generations is used. To reduce statistical errors, each test is repeated 30 times independently and the mean results are used in the comparisons.

3.1. Benchmark functions

The ten basic benchmark problems summarised in Table 1, can be classified into two groups. The first five functions - are unimodal functions. The unimodal functions here are used to test if MBOA-BIDE can maintain the fast-converging feature compared with the other methods. The next five functions - are multimodal functions with many local optima. These functions can be used to test the global search ability of the algorithm in avoiding premature convergence.

3.2. The effect of population size N

We set MBOA-BIDE with different population size (= 10, 40, 50, 100, 150 and 200). The results of different population size are presented in Table 2. From Table 2, we can see that population size with 40 is providing the best results in eight of the ten selected functions.

In this study, MBOA-BIDE with different population size are ranked based on their mean performances. They are ranked according to their performances using a standard competition ranking scheme. In competition ranking, algorithms receive the same rank if their performances are same. The next performing algorithm is

assigned a rank with a gap (gap is determined based on the number of equally performing algorithms). Table 3 provides the ranks of the different population size and the average rank for all the functions based on mean performances. Based on the average ranking, the order of performance obtained is = 40 followed by = 50, = 10, = 100, = 150 and = 200 respectively.

Figure 1 presents the histograms that indicate the number of times each population size have achieved the ranks in the range of 1 to 6. It can be seen that = 40 achieves the top rank as compared to the other different population size.

3.3. The effect of magnetic field

To study the effects of in MBOA-BIDE, we use, and for testing the performance of MBOA- BIDE. Firstly we suppose is constant (= 1, 3, 5, 7, 10), and study the effect of on test functions. Secondly, we also study the effect of varying with generation increases as follows:

・ is linearly increases from 1 to10 (= 1 - 10 LINER).

・ is exponentially increases from 1 to 10 (= 1 - 10 EXP )

・ is linearly increases from 1 to 100 (= 1 - 100 LINER)

・ is exponentially increases from 1 to 100 (= 1 - 100 EXP).

The results are shown in Table 4. From Table 4, for, we can see that when is constant, = 10, the method can achieve better performance, when = 1 - 100 LINER can achieve better performance on. For, when = 3 and = 1 - 100 EXP, the method can achieve better performance. For, we can see that when = 1 and = 1 - 10 LINER can achieve better performance.

Figure 2 Presents the line chart and histograms that indicate the mean, best and median values each have achieved for, respectively. From Figure 2, we can see when = 1 - 100 EXP, MBOA-BIDE achieve the

performance on.

3.4. The Effect of c₁ and c₂

Firstly we suppose that and is constant, and study the effect of and on three test functions. We set + = 1, and with different values (0.1, 0.3, 0.5, 0.7, 0.9). Secondly, we also study the effect of

and varying with generation increases. The parameter settings are as follows:

・ = 0 - 1 L: is linearly increases from 0 to1, = 1 -;

・ = 0 - 1 L: is linearly increases from0 to1. = 1 -;

・ = 0.1 - 1 E: is exponentially increases from 0.1 to1, = 1 -;

・ = 0.1 - 1 E: is exponentially increases from 0.1 to 1, = 1 -;

・ = 0 - 2 L: is linearly increases from 0 to2, = 2 -;

・ = 0 - 2 L: is linearly increases from0 to2, = 2 -;

The statistical results are shown in Table 5.

From Table 5 and Table 6, we can see that for, = 0.1 - 1 E obtain the best performance. For and, = 0 - 2 L obtain the best performance. and based on the average ranking, the order of performance obtained is = 0 - 1 L followed by = 0 - 2 L, = 0 - 1 L, = 0 - 2 L, = 0.3, = 0.1, = 0.1 - 1 E, = 0.9, = 0.7, = 0.1-1E and = 0.5, respectively.

4. Conclusion

In this paper, by analyzing the performance of different parameters settings of MBOA-BIDE, we can see that when = 40 - 50, is exponentially increases from 1 to 100, is linearly increases from 0 to 1. = 1 -, MBOA-BIDE obtain the better performance. The experiment results show that the proposed algorithm is

sensitive to parameters settings on some functions.

Acknowledgements

This work is partially supported by the National Natural Science Foundation of China under Grant No.61075113, the Excellent Youth Foundation of Heilongjiang Province of China under Grant No. JC201212, the Fundamental Research Funds for the Central Universities No. HEUCFX041306.

Cite this paper

Hongwei Mo,Lili Liu,Jiao Zhao, (2015) Performance Research on Magnetotactic Bacteria Optimization Algorithm with the Best Individual-Guided Differential Interaction Energy. Journal of Computer and Communications,03,127-136. doi: 10.4236/jcc.2015.35016

References