Journal of Computer and Communications
Vol.03 No.05(2015), Article ID:56577,9 pages
10.4236/jcc.2015.35008
Hybrid ARIMA/RBF Framework for Prediction BUX Index
Dušan Marček
Research Institute of the IT4Innovations Centre of Excellence, The Silesian University in Opava, Bezruc Square 13, 74601 Opava, Czech Republic
Email: Dusan.Marcek@fpf.slu.cz, Dusan.Marcek@fri.uniza.sk


Received March 2015

ABSTRACT
In this paper, we construct and implement a new architecture and learning method of customized hybrid RBF neural network for high frequency time series data forecasting. The hybridization is carried out using two running approaches. In the first one, the ARCH (Autoregressive Conditionally Heteroscedastic)-GARCH (Generalized ARCH) methodology is applied. The second modeling approach is based on RBF (Radial Basic Function) neural network using Gaussian activation function with cloud concept. The use of both methods is useful, because there is no knowledge about the relationship between the inputs into the system and its output. Both approaches are merged into one framework to predict the final forecast values. The question arises whether non-linear methods like neural networks can help modeling any non-linearities being inherent within the estimated statistical model. We also test the customized version of the RBF combined with the machine learning method based on SVM learning system. The proposed novel approach is applied to high frequency data of the BUX stock index time series. Our results show that the proposed approach achieves better forecast accuracy on the validation dataset than most available techniques.
Keywords:
High Frequency Data, Statistical Forecasting Models, Rbf Neural Networks, Machine Learning

1. Introduction
One of the reason computers started to apply in time series modeling was the study of Bollershev [1] where he proved the existence of nonlinearity in financial high frequency data. Over the past ten years statisticians and academics of computer science have developed new forecasting techniques based on probabilistic theory such as the use of Kalman filter, threshold autoregressive models, the ARCH/GARCH family of models, and latest information technologies respectively such as probabilistic or believe networks, soft, neural and granular computing that help to predict future values of high frequency financial data. At the same time, the field of financial econometrics and statistics have undergone various new developments, especially in financial models, stochastic volatility such as models for managing financial risk [2]-[4], methods based on the extreme value theory [5], Lévy models [6], methods to assess and control financial risk, methods based on time intensity models, usage copulas and implementing risk systems [7].
The first techniques of machine learning applied into time series forecasting were artificial neural networks (ANN). As ANN was an universal approximator, it was believed that these models could perform tasks like pattern recognition, classification or predictions [8]. Today, according to some studies [9], ANNs are the models having the biggest potential in predicting financial time series. The reason for attractiveness of ANNs for financial prediction can be found in works of Hill et al. [10], where authors showed that ANNs works best in connection with high-frequency financial data. Lately, time series prediction becomes one of the most important aspects of time series Data Mining, which has received a growing attention. While the first application of ANNs into financial forecasting perceptron’s network the simplest feed forward neural network was used [11], nowadays it is mainly RBF network [12] that is being used for this as they showed to be better approximators than the perceptron type networks [13].
Firstly, in this article we analyse, discuss and compare the forecast accuracy from models which are derived from competing statistical and neural network specifications. Secondly the hybrid ARCH-GARCH and RBF NN (Radial Basic Function Neural Network) architectures for time series prediction are proposed and their forecasting performance is evaluated and compared with SVM (Support Vector Machines) approach. The aim of the paper is to explain achieved aspects of both statistical and soft computing approaches for quantifying forecast accuracy applied to daily BUX index time series and assess the prediction performance of novel models based on the hybridization of these separate approaches.
The paper is organized as follows. In Section 2 we briefly describe the basic knowledge of ARCH-GARCH models and their variants: EGARCH and PGARCH models. Section 3 presents the data, conduct some preliminary analysis of the time series and demonstrate the forecasting abilities of ARMA (AutoRegressive Moving Average)-ARCH/GARCH models. Section 4 introduces RBF neural networks and proposes a novel Evolutionary RBF Network (ERBFN) that is based on RBF network and ARCH/GARCH models. Section 5 shows the forecasting performance SVM system. In Section 6 we put an empirical comparison. Section 7 concludes the paper and proposes future work.
2. Some ARCH/GARCH Models for Financial Data
ARCH-GARCH models are designed to capture certain characteristics that are commonly associated with financial time series. They are among others: fat tails, volatility clustering, persistence, mean-reversion and leverage effect. As far as fat tails, it is well known that the distribution of many high frequency financial data have fatter tails than normal distribution.
The first model that provides a systematic framework for volatility modelling is the ARCH model. This model was proposed by Engle [14]. Bollerslev [1] proposed a useful extension of Engle’s ARCH model known as the generalized ARCH (GARCH) model for time sequence {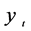 } in the following form
} in the following form
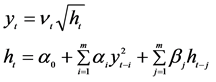 (1)
(1)
where {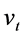 } is a sequence of IID (Independent Identical Distribution) random variables with zero mean and unit variance.
} is a sequence of IID (Independent Identical Distribution) random variables with zero mean and unit variance. 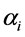 and
and 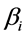 are the ARCH and GARCH coefficients, ht represents the conditional variance of time series conditional on all the information to time t -1, It-1.
are the ARCH and GARCH coefficients, ht represents the conditional variance of time series conditional on all the information to time t -1, It-1.
In the literature several variants of basic GARCH model (1) has been derived. Nelson [15] proposed the following exponential GARCH model abbreviated as EGARCH to allow for leverage effects in the form
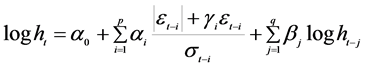 (2)
(2)
The basic GARCH model can be extended to allow for leverage effects. This is performed by treating the basic GARCH model as a special case of the power GARCH (PGARCH) model proposed by Ding, Granger and Engle [16]
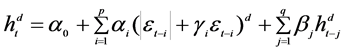 (3)
(3)
where d is a positive exponent, and 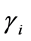 denotes the coefficient of leverage effects.
denotes the coefficient of leverage effects.
Another ARCH-GARCH models as the ARCH-GARCH regression and ARCH-GARCH mean model can be found in [17].
3. An Application of ARCH-GARCH Models
We illustrate the statistical ARCH-GARCH methodology for daily BUX stock indexes1 as a proxy to the Hungarian stock market to study the development of forecasting model. The sample period is from January 7, 2004 to December 31, 2012 and has 2255 observations (see Figure 1). This period was chosen purposely to investigate forecasting accuracy during time with a special emphasis on the resolution of behavior in the time during the global financial crisis of 2008-09, and also in post crisis period of 2010-12. To build a forecast model the sample period for analysis (January 2004 to June 2007 so called the training data set) was defined, i.e. the period over which the forecasting model can be developed and the ex post forecast period (July 2007 to December 2012) so called validation or ex post data set. By using only the actual and forecast values within the ex post forecasting period only, the accuracy of the model can be calculated. It is clear from the time plot of both datasets the series are not stationary since their graphs show a trend, but after differencing their become stationary.
The main purpose of time series analysis is to understand the underlying mechanism that generates the observed data, in turn, to forecast future values. Typically, these processes are described by a class of linear models called autoregressive integrated moving average (ARIMA) models. Tentative identification of an ARIMA time series model is done through analysis of actual historical data. The primary tools used in identification process are autocorrelation function (ACF) and partial autocorrelation function (PACF). The theoretical ACF and PACF are unknown and must be estimated by the sample ACF and PACF.
The relevant lag structure of potential inputs was analyzed using traditional statistical tools, i.e. using the autocorrelation function (ACF), partial autocorrelation function (PACF) and the Akaike information criterion (AIC): we looked to determine the maximum lag for which the PACF coefficient was statistically significant and the lag given the minimum AIC. According to these criterions the ARMA model was specified as the ARIMA(1,1,0) process.
High frequency financial data, like our BUX index reflect a stylized fact of changing variance over time. An appropriate model that would account for conditional heteroscedasticity should be able to remove possible nonlinear pattern in the data. Various procedures are available to test an existence of ARCH or GARCH. A commonly used test is the LM (Lagrange Multiplier) test [14]. The LM test performed on the BUX time series indicates presence of autoregressive conditional heteroscedasticity. For estimation the coefficients of an ARCH or GARCH type model the maximum likelihood procedure was used. The quantification of the model was performed by means of the R2.6.0 software and resulted into the ARIMA(1,1,0)/EGARCH(1,1,1) model where the ARIMA(1,1,0) process has the form
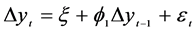 (4)
(4)
Figure 1. Graph of real BUX index.
where 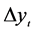 are first differences of the BUX time series,
are first differences of the BUX time series, 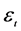 are reziuals
are reziuals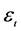 , i.e. independent random variable drawn from stable probability distribution with mean zero and variance ht.. The estimation results of ARIMA(1,1,0)/EGARCH(1,1,1) process for BUX index time series are given in Table 1 and Table 2.
, i.e. independent random variable drawn from stable probability distribution with mean zero and variance ht.. The estimation results of ARIMA(1,1,0)/EGARCH(1,1,1) process for BUX index time series are given in Table 1 and Table 2.
Graph of the fitted and the forecast values for the estimation and ex post periods are presented in Figure 2.
4. Evolutionary RBF Network
The structure of a neural network is defined by its architecture. In Figure 3 the architecture is depicted for classic RBF NN where each circle or node represents the neuron. This neural network consists an input layer with input vector x and an output layer with the output value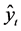 . The output signals of the hidden layer are calculated as
. The output signals of the hidden layer are calculated as
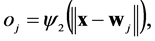 (5)
(5)
where x is a k-dimensional neural input vector, 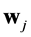 represents the hidden layer weights,
represents the hidden layer weights, 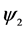 are radial basis
are radial basis
Figure 2. The actual and fitted values for BUX index?statistical approach (validation data set Jun 2007-Dec 2012).
Figure 3. RBF neural network architecture.
Table 1. Estimation results of ARIMA(1,1,0) model for BUX index.
Table 2. Estimation results of EGARCH(1,1,1) model for BUX index.
(Gaussian) activation functions. Note that for an RBF network, the hidden layer weights 



where N is the size of training data samples, s denotes the number of the hidden layer neurons (RBF neurons) and 

= 
where 

Recently, a lot of scholars have developed hybrid forecasting systems []. For example models for financial data systems which focus on parametric structural models, including logit or probit models of warning economic indicators to predict crises [19] [20], and models which utilize techniques of computational intelligence such ANN, fuzzy logic systems and genetic algorithm, artificial intelligence and machine learning [21].
Next, we will combine the RBF neural network according to the architecture depicted in Figure 3 with the statistical ARMA(1,1,0)/EGARCH(1,1,1) model and with estimated coefficients given in Table 1 and Table 2 respectively in one unified framework. The scheme of such proposed hybrid model is depicted in Figure 4. The thought of this proposal consists in the economic theory of co-integrated variables which are related by an error correction model [22]. The simple mean Equation (4) can be interpreted as the long-run relationship and thus it entails a systematic co-movement between variables 



The mentioned hybrid model consists of the following components. External inputs which represent input data, in our case the BUX indexes of historical-rates. Input data enter the ARIMA forecasting model which produces one output: the ex-post residuals. These residuals enter together with external inputs the hyrid ERBF NN forecasting model which generates the ERBF NN ex post forecasts.
As can be seen in Figure 4, the proposed hybrid forecasting systems are two or more prediction models. It can be proposed several types of hybrid forecasting systems depending on the combination and utilization of the various components which are included into the system. For example, we investigated also another hybrid system in which the ERBF NN was replaced by the classic neural network of perceptron type with one hidden layer. The architecture of this neural network is similar to the classic RBF NN architecture. The difference is that all processing neurons in the hidden layer have the tanh activation functions and all the weights 
5. Support Vector Machines Learning
Despite the fact that RBF neural networks possess a number of attractive properties such as the universal
Figure 4. The scheme of the proposed hybrid forecasting model (see text for details).
approximation ability and parallel structure, they still suffer from problems like the existence of many local minima and the fact that it is unclear how one should choose the number of hidden units. Support Vector Machines (SVM) are learning systems that use a hypothesis space of linear function in high dimensional feature space, trained with learning algorithm from optimization theory that implements a learning bias derived from statistical learning theory. Recently, SVMs have been introduced by Vapnik [24]. SVR is an extension of the support vector machine algorithm for numeric prediction. Its decision boundary can be expressed with a few support vectors. When used with kernel functions, it can create complex nonlinear decision boundaries while reducing the computational complexity. Nonlinear Support Vector Regression (SVR) is frequently interpreted by using the training data set {




where 
perform SVR one optimizes the cost function 

function which is defined as follows
and the weights vector norm 
This leads to the optimization problem min
subject to
where 
Finally, the SVR nonlinear function estimation takes the form

where so called kernel trick was applied 


6. Results and Empirical Comparison
ERBFN and SVM model were trained using the variables and data sets as the ARMA(1,1,0)/EGARCH(1,1,1) model above. In the ERBFN framework, the non-linear forecasting function f(x) was estimated according to the expressions (6) with RB function 
From Table 3 it is shown that all forecasting models used are very accurate. The development of the error rates on the validation data sets showed a high inherent deterministic relationship of the underlying variables.
Figure 5. The actual and fitted values for BUX index-ERBFN model (the validation data sets Jun 2007-Dec 2012).
Figure 6. The actual and fitted values for BUX index-SVM model (the validation data sets Jun 2007-Dec 2012).
Table 3. Statistical summary measures of model’s ex post forecast accuracy for ARIMA(1,1,0)/EGARCH(1,1,1) model and SVM model.
Though promising results have been achieved with both approaches, for the chaotic financial time markets a purely linear (statistical) approach for modeling relationships does not reflect the reality. The hybrid system based on ERBFN not only detected the functionality between the underlying variables and the BUX indexes as well as the short-run dynamics.
7. Conclusions
In the present paper we proposed two approaches for predicting the BUX time series. The first one was based on the latest statistical ARIMA/ARCH methodologies, the second one was on neural version of the statistical model and SVR.
After performed demonstration it was established that forecasting model based on SVR model is better than ARIMA/ARCH one to predict high frequency financial data for the Malaysia KLCI-Price Index time series. The direct comparison of forecast accuracies between statistical ARCH-GARCH forecasting models and its neural representation, the experiment with high frequency financial data indicates that all investigated methodologies yield very little MAPE (Mean Percentage Absolute Error) values. Moreover, our experiments show that neural forecasting systems are economical and computational very efficient, well suited for high frequency forecasting. Therefore they are suitable for financial institutions, companies, medium and small enterprises. In the future research we plan to extend presented methodologies by applying fuzzy logic systems to incorporate structured human knowledge into workable learning algorithms.
Acknowledgements
This work was supported by the European Regional Development Fund in the IT4Innovations Centre of Excellence project (CZ.1.05/1.1.00/02.0070).
Cite this paper
Dušan Marček, (2015) Hybrid ARIMA/RBF Framework for Prediction BUX Index. Journal of Computer and Communications,03,63-71. doi: 10.4236/jcc.2015.35008
References
- 1. Bollershev, T. (1986) Generalized Autoregressive Conditional Heteroskedasticity. Journal of Econometrics, 31, 307- 327. http://dx.doi.org/10.1016/0304-4076(86)90063-1
- 2. Jorion, P. (2006) Value at Risk. In: McGraw-Hill Professional Financial Risk Manager Handbook: FRM Part I/Part II. John Wiley & Sons, Inc., New Jersey.
- 3. Jorion, P. (2009) Financial Risk Manager Handbook. John Wiley & Sons, Inc., New Jersey.
- 4. Zmeskal, Z. (2005) Value at Risk Methodology under Soft Conditions Approach (Fuzzy-Stochastic Approach). European Journal of Operational Research, 161, 337-347. http://dx.doi.org/10.1016/j.ejor.2003.08.048
- 5. Glosten, L.R., Jaganathan, R. and Runkle, D.E. (1993) On the Relation between the Expected Value and the Volatility of the Nominal Excess Returns on Stocks. Journal of Finance, 48, 1779-1801. http://dx.doi.org/10.1111/j.1540-6261.1993.tb05128.x
- 6. Bertoin, J. (1998) Lévy Processes of Normal Inverse Gaussian Type. Finance and Statistics, No. 2, 41-68.
- 7. Bessis, J. (2010) Risk Management in Banking. John Wiley & Sons Inc., New York.
- 8. Hertz, J., Krogh, A. and Palmer, R.G. (1991) Introduction to the Theory of Neural Computation. Westview Press.
- 9. Gooijer, J.G. and Hyndman, R.J. (2006) 25 Years of Time Series Forecasting. Journal of Forecasting, 22, 443-473. http://dx.doi.org/10.1016/j.ijforecast.2006.01.001
- 10. Hill, T., Marquez, L., O’Connor, M. and Remus, W. (1994) Neural Networks Models for Forecasting and Decision Making. International Journal of Forecasting, 10, 5-15. http://dx.doi.org/10.1016/0169-2070(94)90045-0
- 11. White, H. (1988) Economic Prediction Using Neural Networks: The Case of IBM Daily Stock Returns. Proceedings of the Second IEEE Annual Conference on Neural Networks, 2, 451-458. http://dx.doi.org/10.1109/ICNN.1988.23959
- 12. Hornik, K. (1993) Some New Results on Neural Network Approximation. Neural Networks, 6, 1069-1072. http://dx.doi.org/10.1016/S0893-6080(09)80018-X
- 13. Mar?ek, D. (2014) Volatility Modelling and Forecasting Models for High-Frequency Financial Data: Statistical and Neuronal Approach. Journal of Economics, 62, 133-149.
- 14. Engle, R.F. (1982) Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica, 50, 987-1007. http://dx.doi.org/10.2307/1912773
- 15. Nelson, D.B. (1991) Conditional Heteroscedasticity in Asset Returns: A New Approach. Econometrica, 59, 347-370. http://dx.doi.org/10.2307/2938260
- 16. Ding, Z., Granger, V.W. and Engle, R.F. (1993) A Long Memory Property of Stock Market Returns and a New Model. Journal of Empirical Finance, 1, 83-106. http://dx.doi.org/10.1016/0927-5398(93)90006-D
- 17. Marcek, D., Marcek, M. and Babel, J. (2009) Granular RBF NN Approach and Statistical Methods Applied to Modelling and Forecasting High Frequency Data. International Journal of Computational Intelligence Systems, 2, 353- 364. http://dx.doi.org/10.1080/18756891.2009.9727667
- 18. Li, D. and Du, Y. (2008) Artificial Intelligence with Uncertainty. Chapman & Hall/CRC, Taylor & Francis Group, Boca Raton.
- 19. Bussiere, M. and Fratzscher, M. (2006) Towards a New Early Warning System of Financial Crises. Journal of Money and Finance, 26, 953-973.
- 20. Yu, L., Lai, K.K. and Wang, S.Y. (2006) Currency Crisis Forecasting with General Regression Neural Networks. International Journal of Information Technology and Decision Making, 5, 437-454. http://dx.doi.org/10.1142/S0219622006002040
- 21. Sohn, I., Oh, K.J., Kim, T.Y. and Kim, D.H. (2009) An Early Warning Systems for Global Institutional Investor at Emerging Stock Markets Based on Machine Learning Forecasting. Expert Systems with Applications, 36, 4951-4957. http://dx.doi.org/10.1016/j.eswa.2008.06.044
- 22. Engle, R.F. and Granger, C.W.J. (1987) Co-Integration and Error Correction Representation, Estimation and Testing. Econometrica, 55, 251-276. http://dx.doi.org/10.2307/1913236
- 23. Banerjee, A.J., Dolado, J.J., Galbrait, J.W. and Hendry, D.F. (1993) Co-Integration, Error Correction, and the Econometric Analysis of Non-Stationary Data. Oxford University Press. http://dx.doi.org/10.1093/0198288107.001.0001
- 24. Vapnik, V. (1995) The Nature of Statistical Learning Theory. Springer Verlag, New-York.
NOTES
1You can obtain these data from www pages at http://www.global-view.com/forex-trading-tools/forex-history.













