Journal of Modern Physics, 2011, 2, 488-497
doi:10.4236/jmp.2011.26059 Published Online June 2011 (http://www.SciRP.org/journal/jmp)
A New Parallel Algorithm for Simulation of Spin-Glass
Systems on Scales of Space-Time Periods of an
External Field
Ashot S. Gevorkyan1,2, Hakob G. Abajyan1, Hayk S. Sukiasyan3
1Institute for Informa tics and Automation Problems, NAS of Armenia, Yerevan, Armenia
2Joint Institute of Nu clear Research, Moscow Reg., Russia
3Institute of Mathematics, NAS of Armenia, Yerevan, Armenia
Received March 25, 2011; revised April 27, 2011; accepted May 7, 2011
Abstract
We study the statistical properties of an ensemble of disordered 1D spatial spin-chains (SSCs) of certain
length in the external field. On nodes of spin-chain lattice the recurrent equations and corresponding inequal-
ity conditions are obtained for calculation of local minimum of a classical Hamiltonian. Using these equa-
tions for simulation of a model of 1D spin-glass an original high-performance parallel algorithm is developed.
Distributions of different parameters of unperturbed spin-glass are calculated. It is analytically proved and
shown by numerical calculations that the distribution of the spin-spin interaction constant in the Heisenberg
nearest-neighboring Hamiltonian model as opposed to the widely used Gauss-Edwards-Anderson distribu-
tion satisfies the Lévy alpha-stable distribution law which does not have variance. We have studied critical
properties of spin-glass depending on the external field amplitude and have shown that even at weak external
fields in the system strong frustrations arise. It is shown that frustrations have a fractal character, they are
self-similar and do not disappear at decreasing of calculations area scale. After averaging over the fractal
structures the mean values of polarizations of the spin-glass on the scales of external field's space-time peri-
ods are obtained. Similarly, Edwards-Anderson’s ordering parameter depending on the external field ampli-
tude is calculated. It is shown that the mean values of polarizations and the ordering parameter depending on
the external field demonstrate phase transitions of first-order.
Keywords: Spin-Glass Hamiltonian, Birkhoff Ergodic Hypothesis, Statistic Distributions, Frustration,
Fractal, Parallel Algorithm, Numerical Simulation
1. Introduction
Spin glasses are prototypical models for disordered sys-
tems which provide a rich source for investigations of a
number of important and difficult applied problems of
physics, chemistry, material science, biology, nanoscience,
evolution, organization dynamics, hard-optimization,
environmental and social structures, human logic sys-
tems, financial mathematics etc (see for example [1-9]).
The considered mean-field models of spin-glasses as a
rule are divided into two types. The first consists of the
true random-bond models, where the couplings between
interacting spins are taken to be independent random
variables [10-12]. The solution of these models is ob-
tained by n-replica trick [10,12] and the invention of
sophisticated schemes of replica-symmetry breaking is
required [12,13]. In the models of second type, the bond-
randomness is expressed in terms of some underlining
hidden site-randomness and is thus of a superficial nature.
However, it has been pointed out in the works [14-16]
that this feature retains an important physical aspect of
true spin-glasses, viz. that they are random with respect
to the positions of magnetic impurities.
As recently shown by authors [17], some type of di-
electrics can be treated as the model of quantum 3D
spin-glass. In particular, it was proved that the initial 3D
quantum problem on space-time scales of an external
field in the direction of wave’s propagation can be re-
duced to two conditionally separable 1D problems,
where one of them describes the classical 1D spin-glass

A. S. GEVORKYAN ET AL.
489
problem with the random environment.
In this paper we discuss in detail statistical properties
of the spin-glass short-range interaction model which
describes an ensemble of 1D spatial spin-chains of cer-
tain length
x
L while taking into account the influence
of an external field. Recall that each spin-chain from
itself represents 1D lattice, where on every node of lat-
tice one random-orientated (3)O spin is located.
In Section 2 the spin-glass problem on 1D lattice is
formulated. Equations for stationary points and corre-
sponding conditions for definition of energy minimum
on lattice nodes (local minimum of energy) are obtained.
The formula for distributions’ computation for different
parameters of spin-glass system are derived.
In Section 3 the exact solutions of recurrent equations
for angles of i + 1-th spin depending on i-th and i + 1-th
spin-spin interaction constant are obtained. The scheme
of parallel simulation of statistical parameters of system
is suggested and the corresponding pseudo-code is ad-
duced.
In Section 4 the numerical experiments for unper-
turbed 1D spin-glass system are adduced, including dis-
tributions of energy, polarization and spin-spin interac-
tion constant.
In Section 5 the statistical properties of spin-glass, on
the scales of space-time periods of external field are in-
vestigated in detail. The distribution of average polariza-
tion on different coordinates and Edwards-Anderson type
ordering parameter of spin-glass system in external field
are investigated.
In Section 6 the obtained theoretical and computa-
tional results are analyzed.
2. Formulation of the Problem
We consider a classical ensemble of disordered 1D spa-
tial spin-chains (SSC) of length
x
L (Figure 1), where
for simplicity is supposed that the interactions between
spin-chains are absent. A specificity of a problem is such
that statistical properties of a system on very short time
intervals t

at which system cannot be thermally re-
laxed are of interest to us. Let us note that for a problem
the following time-correspondences take place
1
<1
T
t  

 , where  is a frequency of an
external field,

is a relaxation time of spin in an ex-
ternal field and T

is the time of thermal relaxation. In
other words we suppose that the spin-glass system is
frozen and nonsusceptible to thermal evolution.
Mathematically such type of spin-glass can be de-
scribed by 1D Heisenberg spin-glass Hamiltonian [1-3]:

11
11
00
.
NN
xx
x
ii iiii
ii
H
NJSShS



 

(1)
where i S describes the i-th spin which is the unit length
vector and has a random orientation, i h describes the
external field which is orientated along the axis x:


00
=cos, = ,=2π,
ixiixx
hhkxxid kL (2)
where 0 h is the amplitude of the external field. In addi-
tion, in expression (1) 1ii
J

characterizes a random in-
teraction constant between i and i + 1 spins which can
have positive as well as negative values (see [1,18]). The
distribution of spin-spin interaction constant will be
found by way of calculations of classical Hamiltonian
problem.
For further investigations, (1) is convenient to write in
spherical coordinates (see Figure 1):
   


1
111
=0
1
=coscoscos
sin sinsin
Nx
xiiiiii
i
ii ii
HN J
h
 
 





 (3)
For the consecutive calculations of problem the equa-
tions of stationary points of Hamiltonian will play a cen-
tral role:
=0,=0,
ii
HH



(4)
where


=,
iii

  are the angles of i-th spin in the
spherical coordinates system (i

is a polar angle and
i

is an azimuthal one).
Using expression (3) and equations (4) it is easy to
find the following system of trigonometrical equations:


1
=1;
1
=1;
sintancoscos= 0,
cossin= 0,.
i
iiii
ii
i
ii ii
ii
Jh
JJJ
 

 







 




(5)
Z
Y
d
0
X
O
S
0
S
1
L
x
x
N
S
S
2
1
x
N
S
Figure 1. A stable 1D spatial spin-chain with random inter-
actions and the length of Lx = d0Nx, where d0 is a distance
between nearest-neighboring spins, Nx designates the num-
ber of spins in chain. The spherical angles φ0 and ψ0 de-
scribe the spatial orientation of S0 spin, the pair of angles
(φ0, ψ0) defines the spatial orientation of the spin Si.

A. S. GEVORKYAN ET AL.
490
In the case when all interaction constants between i-th
spin with its nearest-neighboring spins 1ii
J
, 1ii
J

and
angles 11 (,)
ii


, (,)
ii

are known, it is possible to
explicitly calculate the pair of angles 11 (,)
ii


. Cor-
respondingly, the i-th spin will be in the ground state (in
the state of minimum energy) if in the stationary point

000
=,
iii

 the following conditions are satisfied:

 
0
0020
>0,
>0,
i
ii
ii i
ii iiii
A
AA A

 


(6)
where

 
02 2
0
002
0
=,
== ,
ii
ii
ii ii
ii ii
AH
AA H

 



 

in addition:
 
1
00
=1;
000
=coscos
tansintancos,
i
ii i
ii ii
iiii
AJ
h
 


















 
0
1
000
=1;
=0,
=coscoscos .
i
ii
i
ii ii
ii ii
A
AJ

 






 (7)
Evidently by Equations (5) and conditions (6) we can
calculate a huge number of stable 1D SSCs which will
allow to investigate the statistical properties of 1D
SSCs ensemble. It is supposed that the average polari-
zation (magnetization) of 1D SSCs ensemble (polariza-
bility of 1D SSC) at absence of external field is equal to
zero.
Now we can construct the distribution function of en-
ergy of 1D SCCs ensemble. To this effect it is useful to
divide the non-dimensional energy axis =

 into
regions 0 0>>>n

 , where 1n and

is a
real energy axis. The number of stable 1D SSC configu-
rations with length of
x
L in the range of energy
[,

  ]

  will be denoted by ()
Lx
M

while the
number of all stable 1D SSC configurations - corre-
spondingly by symbol

=1
=n
full
L
Lj
j
xx
MM

. Accord-
ingly, the energy distribution function of ensemble may
be defined by expressions [19]:
  
0
;= ,
f
ull
LLL
xxx
FdTMM 




0
00
1
;;1,
lim
n
Ljj L
xx
nj
FdT FdTd 

 

 (8)
where the second expression shows normalization condi-
tion of distribution function to unit. By similar way we
can define also distributions of polarization and spin-spin
interaction constant.
3. Simulation Algorithm
Using the following notation:

111 1
=cos,=sin,
iii ii

 
 (9)
equations system (5) may be transformed to the follow-
ing form:
22
1111 1
2111
1tan1=0,
=0,
iiii ii
ii ii
CJ
CJ


 


 



(10)
where parameters 1 C and 2 C are defined by expres-
sions:


11 111
21 11
=sintan coscos
cos,
=cossin .
iiiiii i
ii
iiii i
CJ
h
CJ



 
 

 




(11)
From the system (11) we can find the equation for the
unknown variable 1i


:
2222
11 2111 2
1tan=0.
iiiiii
CCJ C 
 
 (12)
We can transform the Equation (12) to the following
equation of fourth order:
222 4
12 1
22 24
2
21212
4sin
22 =0,
sin
ii
ii
ACC
ACCCC








 

(13)
where
222
22
112
=.
cos sin
ii ii
AJC C


 (14)
Discriminant of Equation (13) is equal to:

 

2
44222
22
212 12
422 2 22
211 2
=2 4
sin sin
=4 .
sin sin
ii
ii
DCA CCACC
CCA CC





From the condition of non-negativity of discriminant
0D we can find the following condition:
22
2
12
0.
sin i
AC C 

 (15)
Further substituting A from (14) into inequality (15)
we can find the new condition to which the interaction
constant between two successive spins should satisfy:
222
11 2
.
ii
J
CC
 (16)
Now we can write the following expressions for un-
known variables 1i


and 1i

:

A. S. GEVORKYAN ET AL.
491

2
22
122
11
221222
22
1311 112
22
12 2
4222 42 2
13112
=,
21cot
cos sin
=,
2
cos cossin
i
ii i
iiiii ii
i
ii i ii ii
C
J
JCCCJCC
CJCJCC


 








 





(17)
where 22
2
312
=.
sin i
CCC


Finally in consideration of (9) for the calculating an-
gles 11 (, )
ii


we find:
22
11
01,01.
ii


  (18)
These conditions are very important for elaborating
correct and high performance simulation algorithm.
Moreover, as shown in [19] the condition (16) excludes
the possibility to get normal distribution for spin-spin
interaction constants in the 1D Heiseberg nearest-
neighboring spin-glass Hamiltonian model.
Algorithm Description
Let us note that the developed algorithm is an iterative
algorithm depending on 1D SSC’s nodes. The first and
second nodes are initialized randomly, then i-th node is
obtained from (2)i-th and (1)i-th layers nodes.
Every node contains the following information:

-polar angle,

-azimuthal angle,
J
-interaction coefficient,
The following parameters are initialized in the fol-
lowing way:
0

and 1

- rand() 2πR
 ;
0

and 1

- acos (rand());
01
J
- rand();
where rand() function generates uniformly distributed
random numbers on the interval (0,1) .
The algorithm pseudo-code is following:
for =1:mn// n separate independent
//sets of problem
for =1:
x
iN
for =1:jR //regenerate i
J
maximum
//R times if needed
for =1: i kL//go through all elements in
//the i-th layer
if conditions (9) are satisfied
begin
//calculate energy on i-th layer,
//calculate polarization on ,
x
y
//and z-axis
//calculate 1i
x
 and 1, i
y
//save i
J
value
....
end
endfor
endfor
endfor
endfor
if (=
x
iN)//reached the
x
N-th layer
begin
//save energy, polarizations values
end
endif
//construct distribution functions of energy

,
//polarization p and interaction constant
J
//calculate the mean value of energy

, polarization
// p, interaction constant
J
and its variance 2
J
.
4. Numerical Experiments
Let us suppose that the ensemble consists of
M
number of spin-chains each of them with the length 100
0
d. For realization of simulation we will use parallel
algorithm the scheme of which is represented in the
Figure 2 (see also [19]). The algorithm works as fol-
lows. Randomly M sets of initial parameters are gener-
ated and parallel calculations of Equation (17) for un-
known variables i
x
and i y transact taking into ac-
count conditions (16) and (18). However only specify-
ing initial conditions is not enough for the solution of
these equations. Evidently these equations can be
solved after the definition of the constant 01
J
, which is
also randomly generated. When the solutions of recur-
rent equations are found, the conditions of stability of
spin on the node (7) are being checked. The process of
simulation proceeds on the current node if the condi-
tions (7) are satisfied. If conditions are not satisfied, the
new constant 01
J
is randomly generated and corre-
spondingly new solutions are found which are checked
later on conditions (7). This cycle is being repeated on
each node until the solutions do not satisfy conditions
of the energy local minimum.
At first we have conducted numerical simulation for
definition of different statistical parameters of the en-
semble which consists of 4 510 spin-chains and at
absence of external field (the case of unperturbed Ham-
iltonian). Note that during simulation we suppose that
spin-chains can be polarized correspondingly up to 20,
40 and 100 percent i.e. the total value of spins sum in
each chain can be within the interval of {5 5},p 
{1010}p

 and { 100100}p

 , where p
designates the polarization of spin-chain. In other words,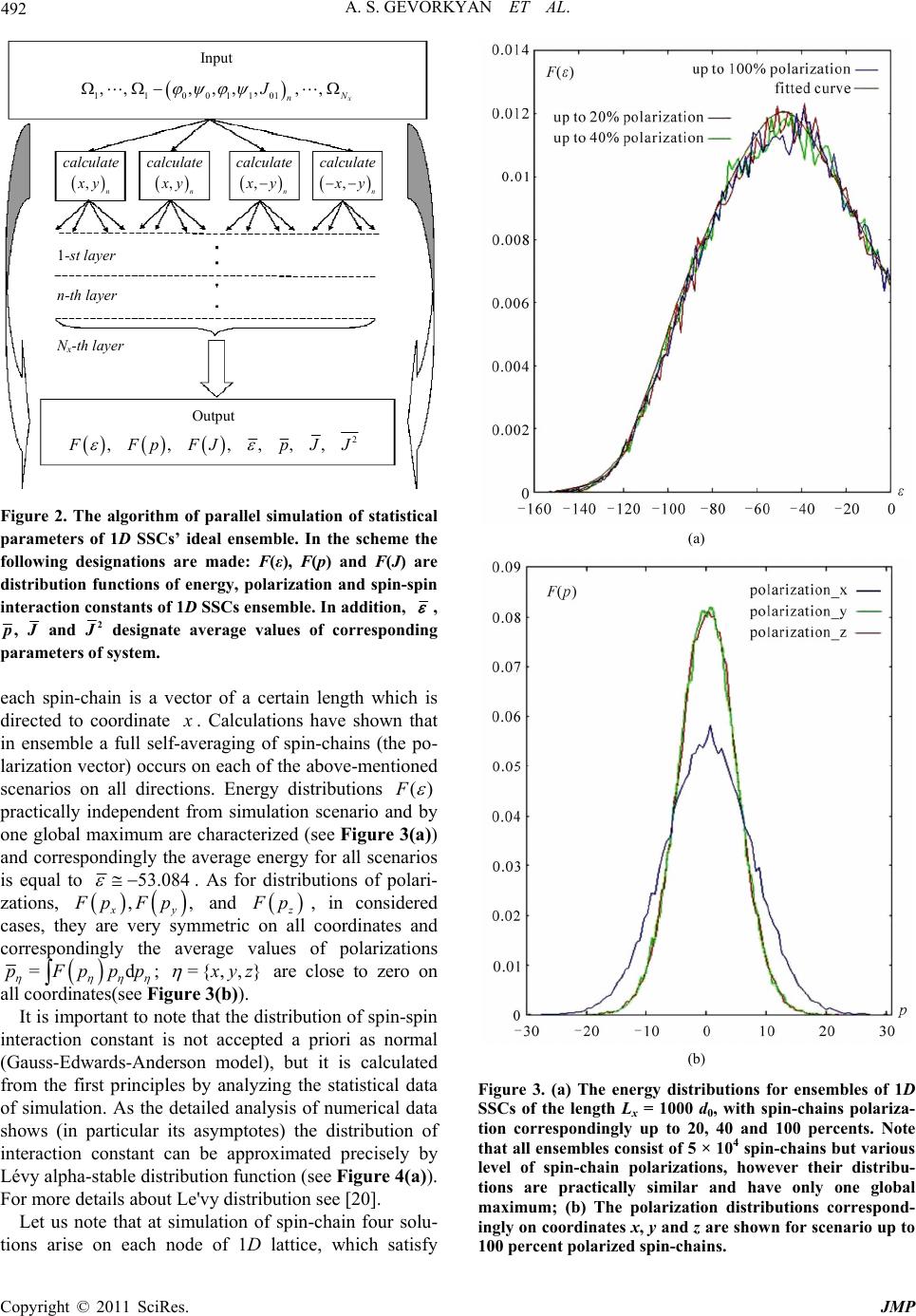

A. S. GEVORKYAN ET AL.
492
Input


11001101
,,,,,, ,,
x
N
n
J    
calculate

,n
x
y
calculate

,n
x
y
calculate


,n
x
y
calculate

,n
x
y
1-s t laye r
n-th layer
N
x
-th layer
Output
  
2
,,,,,,FFpFJpJJ 
Figure 2. The algorithm of parallel simulation of statistical
parameters of 1D SSCs’ ideal ensemble. In the scheme the
following designations are made: F(ε), F(p) and F(J) are
distribution functions of energy, polarization and spin-spin
interaction constants of 1D SSCs ensemble. In addition,

,
p,
J
and 2
J
designate average values of corresponding
parameters of system.
each spin-chain is a vector of a certain length which is
directed to coordinate
x
. Calculations have shown that
in ensemble a full self-averaging of spin-chains (the po-
larization vector) occurs on each of the above-mentioned
scenarios on all directions. Energy distributions ()F

practically independent from simulation scenario and by
one global maximum are characterized (see Figure 3(a))
and correspondingly the average energy for all scenarios
is equal to 53.084

 . As for distributions of polari-
zations,


,,
xy
F
pFp and

z
F
p, in considered
cases, they are very symmetric on all coordinates and
correspondingly the average values of polarizations

=dpFppp


; ={ ,,}
x
yz

are close to zero on
all coordinates(see Figure 3( b)).
It is important to note that the distribution of spin-spin
interaction constant is not accepted a priori as normal
(Gauss-Edwards-Anderson model), but it is calculated
from the first principles by analyzing the statistical data
of simulation. As the detailed analysis of numerical data
shows (in particular its asymptotes) the distribution of
interaction constant can be approximated precisely by
Lévy alpha-stable distribution function (see Figure 4(a)).
For more details about Le'vy distribution see [20].
Let us note that at simulation of spin-chain four solu-
tions arise on each node of 1D lattice, which satisfy
(a)
(b)
Figure 3. (a) The energy distributions for ensembles of 1D
SSCs of the length Lx = 1000 d0, with spin-chains polariza-
tion correspondingly up to 20, 40 and 100 percents. Note
that all ensembles consist of 5 × 104 spin-chains but various
level of spin-chain polarizations, however their distribu-
tions are practically similar and have only one global
maximum; (b) The polarization distributions correspond-
ingly on coordinates x, y and z are show n for scenario up to
100 percent polarized spin-chains.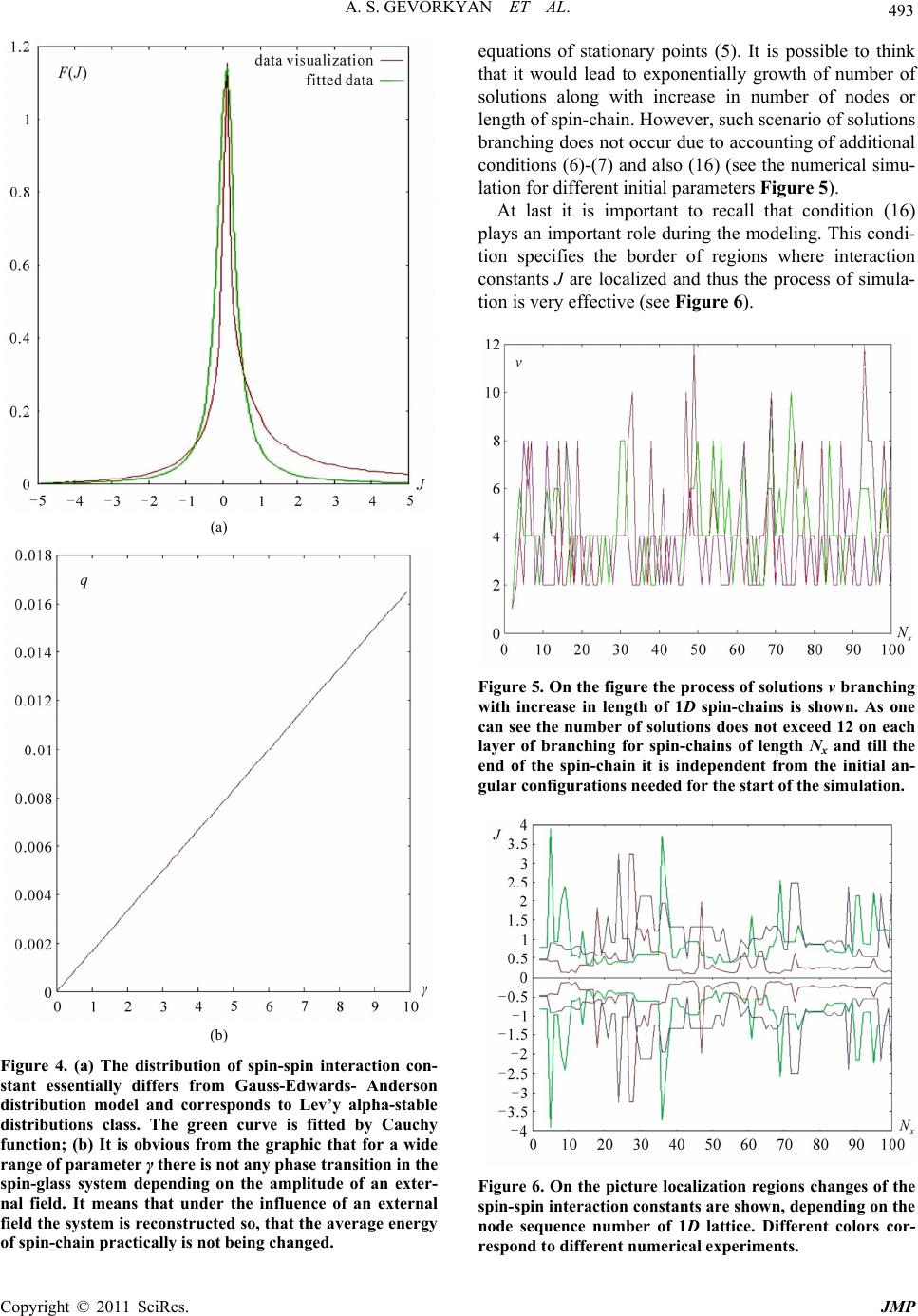

A. S. GEVORKYAN ET AL.
493
(a)
(b)
Figure 4. (a) The distribution of spin-spin interaction con-
stant essentially differs from Gauss-Edwards- Anderson
distribution model and corresponds to Lev’y alpha-stable
distributions class. The green curve is fitted by Cauchy
function; (b) It is obvious from the graphic that for a wide
range of parameter γ there is not any phase transition in the
spin-glass system depending on the amplitude of an exter-
nal field. It means that under the influence of an external
field the system is reconstructed so, that the average energy
of spin-chain practically is not being changed.
equations of stationary points (5). It is possible to think
that it would lead to exponentially growth of number of
solutions along with increase in number of nodes or
length of spin-chain. However, such scenario of solutions
branching does not occur due to accounting of additional
conditions (6)-(7) and also (16) (see the numerical simu-
lation for different initial parameters Figure 5).
At last it is important to recall that condition (16)
plays an important role during the modeling. This condi-
tion specifies the border of regions where interaction
constants J are localized and thus the process of simula-
tion is very effective (see Figure 6).
Figure 5. On the figure the process of solutions ν branching
with increase in length of 1D spin-chains is shown. As one
can see the number of solutions does not exceed 12 on each
layer of branching for spin-chains of length Nx and till the
end of the spin-chain it is independent from the initial an-
gular configurations needed for the start of the simulation.
Figure 6. On the picture localization regions changes of the
spin-spin interaction constants are shown, de pending on the
node sequence number of 1D lattice. Different colors cor-
respond to different numerical experiments.

A. S. GEVORKYAN ET AL.
494
5. Statistical Properties of Ensemble in
External Field
Using the obvious similarity between temperature T of
usual statistical ensemble and the average energy coming
on one spin 0=
x
N

 we can define the partition
function as follows:


1
0
d;
d
;=exp ,
44
Nx
xHN g
ZgJ
 







 (19)
where J describes the set of spin-spin interaction con-
stants in chain.
The integration in the expression (19) in above-men-
tioned model may start from the end of the chain (see
[21]). When integrating over the solid angle di

we
take the direction of the vector

0
1Sh ii ii
Jp
 as a
polar axis and it is easy to obtain the following expres-
sion:



1
=0
2
20 0
111
0
sinh
;= ,
1
;, =2cos.
Nxi
ii
iiiii iiiii
G
ZgJG
Gg JJphJph 





(20)
Assuming that the distribution of spin 1i S

around
the field i h direction is isotropic, one can perform an
integration over the angle i

and after simple calcula-
tions find:


1π
0
=0 0
1
01
=0
sinh 1
,; =sind
2
1
=;,,
Nxiii
ii
Nx
iii
ii
G
Zg JG
gJ
b















(21)
where

01
0
1
0
0
1
2
0
;,= coshcosh,
1
=,
2
=.
iiiii
iiii
iiii
gJa a
aJph
bJph














Now using the expression (21) we can average the
partition func tion by distribution ()
F
J:
 
1
0
000
0
=0 ,
1
,,;= ,;,
Nx
i
Jiij
J
ZgZg Jg J
b
 



(22)
where


011 011
.dd
N
NNN
J
x
xxx
FJ FJJJ

  .
Like in the usual thermodynamics, Helmholtz free en-
ergy for 1D SSC ensemble may be specified in the fol-
lowing kind:


000 0
,=ln ,,<0.Qg Zg  (23)
Note that all thermodynamic properties of the statistical
system in this case may be obtained by means derivation
of the free energy by external field parameters g. After
the derivation of the free energy by 0
h we can find:




1
0
=0
0
,1
,==1 coth,
Nx
xii
i
Qg
qNy y
h





(24)
where

0
00 00
0
=,=,=cos,
=, =2π.
iNi
x
iN x
x
hhph ykx
xidk N

As calculations show, the free energy derivation line-
arly depends on

parameter. The last result testifies
the absence of a phase transition on this parameter (see
Figure 4(b)). Thereby a logical question arises - are
there phase transitions in considered system depending
on other parameters?
To answer this question we will investigate the be-
havior of the average value of polarization depending on
parameter

or the value of an external field.
Using the definition (8) we can calculate the polariza-
tion distribution on coordinates

,Fp


, where
=,,.
x
yz

As numerical simulation shows, distribu-
tions of polarizations depending on parameter

are
strongly frustrated [22] and these frustrations do not dis-
appear at regular dividing of computation region (see
Figures 7(a), (b), (c)). Moreover, at each division a
self-similar structure is conserved which testifies about
its fractal character. The dimensionality of fractal struc-
ture is calculated by simple formula:


=lnln ,DnN

 (25)
where n is the number of partitions of the structure size,
and N is the number of placing of the initial structure.
The calculation particularly shows, that at value of
= 0.00425

dimensionality 1.2095
x
D. In a similar
manner
y
D and
z
D can be calculated. It is obvious
that at increasing

all of them converge to 1.
At last we will pass to a question on average value of
polarization. Namely, how to calculate it? Taking into
account above-mentioned, it is obvious that the average
value of polarization (magnetization) must be calculated
by following formula:
 
1
==,d
lim i
M
f
if
PpFppp
M




 (26)
where the slanting bracket .
f
stands for averaging of
expression by the fractal structure which itself represents
an arithmetic mean. As follows from the Figure 8(a),
after averaging on fractal structures the average value of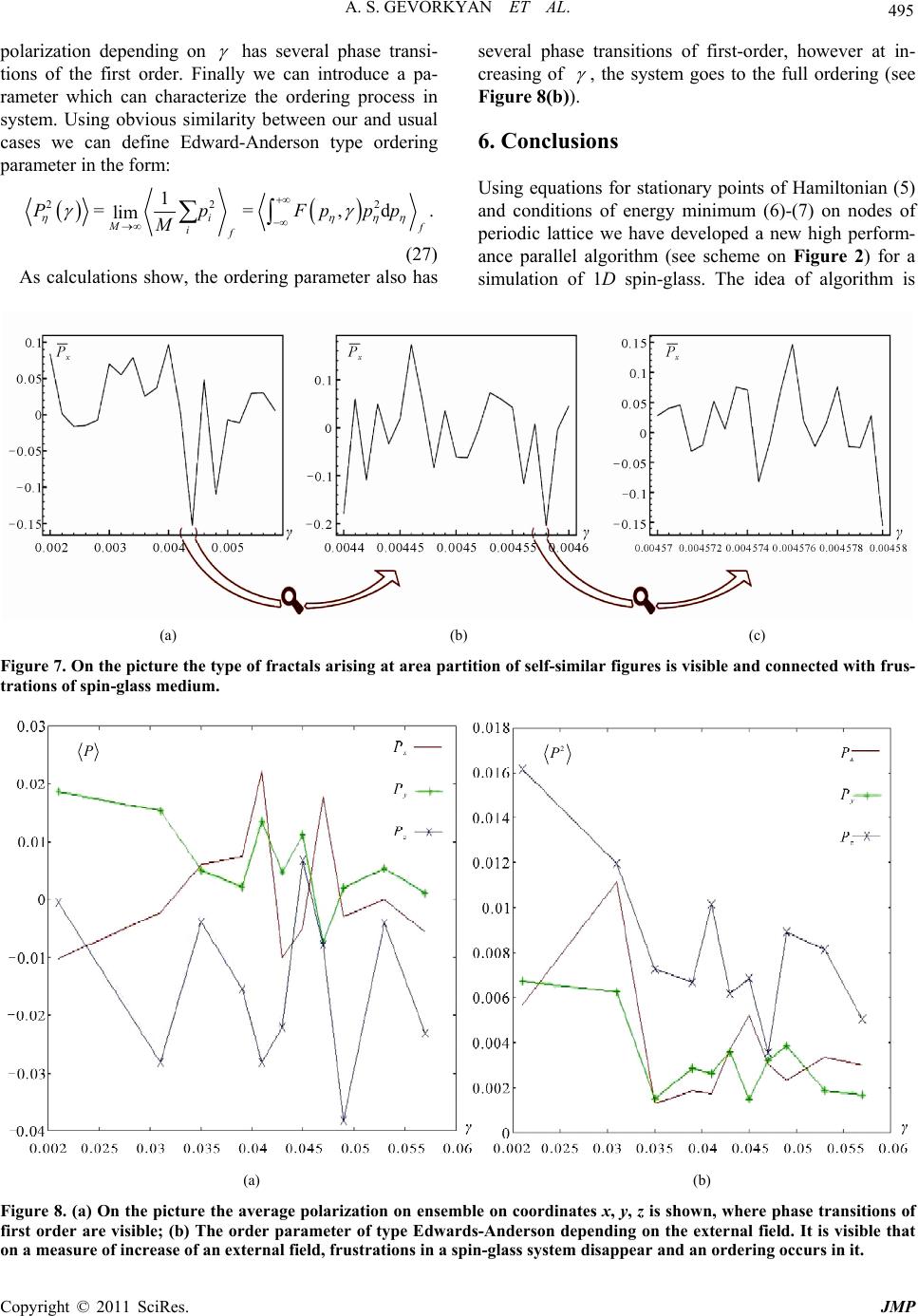

A. S. GEVORKYAN ET AL.
495
polarization depending on

has several phase transi-
tions of the first order. Finally we can introduce a pa-
rameter which can characterize the ordering process in
system. Using obvious similarity between our and usual
cases we can define Edward-Anderson type ordering
parameter in the form:
 
22 2
1
==,d.
lim i
M
f
if
PpFppp
M




 
(27)
As calculations show, the ordering parameter also has
several phase transitions of first-order, however at in-
creasing of

, the system goes to the full ordering (see
Figure 8(b)).
6. Conclusions
Using equations for stationary points of Hamiltonian (5)
and conditions of energy minimum (6)-(7) on nodes of
periodic lattice we have developed a new high perform-
ance parallel algorithm (see scheme on Figure 2) for a
simulation of 1D spin-glass. The idea of algorithm is
(a) (b) (c)
Figure 7. On the picture the type of fractals arising at area partition of self-similar figures is visible and connected with frus-
trations of spin-glass medium.
P
2
P
(a) (b)
Figure 8. (a) On the picture the average polarization on ensemble on coordinates x, y, z is shown, where phase transitions of
first order are visible; (b) The order parameter of type Edwards-Anderson depending on the external field. It is visible that
on a measure of increase of an external field, frustrations in a spin-glass system disappear and an ordering occurs in it.

A. S. GEVORKYAN ET AL.
496
based on the construction of stable spin-chains of certain
lengths. We have shown that the number of spin-chains
(the simulation number) can be considered as a “timing”
parameter as in case of dynamic system and the ergodic
properties of system can be studied depending on this
parameter. It is shown by numerical experiments that
distribution functions of different parameters of the sys-
tem after 2
x
N simulations converge to the equilibrium
values. In other words, system which consists of 2
x
N
number spin-chains satisfies Birkhoff's ergodicity condi-
tions. We have shown that the distribution of spin-spin
interaction constants can be found directly by way of
calculations of classical Equations (5) and analysis of
statistical data of simulation. It is theoretically shown
(see inequality (16)) that at least for the 1D spin-glass
problem the distribution of the spin-spin interaction con-
stants can not be Gauss-Edwards-Anderson type. In par-
ticular, the analysis of numerical data of simulation
shows that they obey to Lévys alpha-stable distribution
law. In other words, if we use the normal distribution in
these problems, we make calculations ineffective, not to
say doubtful.
As it is shown, the derivative of a free energy (24)
does not have a phase transition depending on the pa-
rameter of an external field’s energy (see Figure 4(b)).
The last means that under the influence of an external
field the essential changes of energy does not occur in
the system. The last, however, does not mean that in the
system a critical phenomena can not occur under the in-
fluence of an external field related to other parameters.
Only through numerical calculations we were able to
show that in the system the phase transitions of first or-
der occur under the influence of weak external field in
the value of average polarization of spin-glass on all co-
ordinates (see Figure 8(a)). As calculations show, the
critical phenomena can be considerable even for weak
fields. For example, they can lead to formation of a su-
perlattice of a dielectric constant in the spin-glass’ me-
dium which can have a wide applications for solutions of
different applied problems.
Finally, it is important to note that the algorithm can
be simply generalized for high dimensional cases and in
particular for 3D case, which means that it will be a very
needed instrument for numerical investigations of above-
mentioned class of problems.
7. References
[1] K. Binder and A. P. Young, “Spin Glasses: Experimental
Facts, Theoretical Concepts and Open Questions,” Re-
views of Modern Physics, Vol. 58, No.4, 1986, pp. 801-
976. doi:10.1103/RevModPhys.58.801
[2] M. Mézard, G. Parisi and M. A. Virasoro, “Spin Glass
Theory and Beyond,” Vol. 9, World Scientific, Singapore,
1987.
[3] A. P. Young, “Spin Glasses and Random Fields,” World
Scientific, Singapore, 1998.
[4] R. Fisch and A. B. Harris, “Spin-Glass Model in Con-
tinuous Dimensionality,” Physical Review Letters, Vol.
47, No. 8, 1981, p.620. doi:10.1103/PhysRevLett.47.620
[5] C. Ancona-Torres, D. M. Silevitch, G. Aeppli and T. F.
Rosenbaum, “Quantum and Classical Glass Transitions in
LiHOxY1-xF4,” Physical Review Letters, Vol. 101, No. 5,
2008, pp. 057201.1-057201.4.
[6] A. Bovier, “Statistical Mechanics of Disordered Systems:
A Mathematical Perspective,” Cambridge Series in Sta-
tistical and Probabilistic Mathematics, No. 18, 2006, p
308.
[7] Y. Tu, J. Tersoff and G. Grinstein, “Properties of a Con-
tinuous-Random-Network Model for Amorphous Sys-
tems,” Physical Review Letters, Vol. 81, No. 22, 1998, pp.
4899-4902. doi:10.1103/PhysRevLett.81.4899
[8] K. V. R. Chary and G. Govil, “NMR in Biological Sys-
tems: From Molecules to Human,” Springer, Vol. 6, 2008,
p. 511.
[9] E. Baake, M. Baake and H. Wagner, “Ising Quantum
Chain is an Equivalent to a Model of Biological Evolu-
tion,” Physical Review Letters, Vol. 78, No. 3, 1997, pp.
559-562. doi:10.1103/PhysRevLett.78.559
[10] D. Sherrington and S. Kirkpatrick, “A Solvable Model of
a Spin-Glass,” Physical Review Letters, Vol. 35, No. 26,
1975, pp. 1792-1796. doi:10.1103/PhysRevLett.35.1792
[11] B. Derrida, “Random-Energy Model: An Exactly Solv-
able Model of Disordered Systems,” Physical Review B,
Vol. 24, No. 5, 1981, pp. 2613-2626.
doi:10.1103/PhysRevB.24.2613
[12] G. Parisi, “Infinite Number of Order Parameters for
Spin-Glasses,” Physical Review Letters, Vol. 43, No. 23,
1979, pp. 1754-1756. doi:10.1103/PhysRevLett.43.1754
[13] A. J. Bray and M. A. Moore, “Replica-Symmetry Break-
ing in Spin-Glass Theories,” Physical Review Letters,
Vol.41, No. 15, 1978, pp. 1068-1072.
doi:10.1103/PhysRevLett.41.1068
[14] J. F. Fernandez and D. Sherrington, “Randomly Located
Spins with Oscillatory Interactions,” Physical Review B,
Vol. 18, No. 11, 1978, pp. 6270-6274.
doi:10.1103/PhysRevB.18.6270
[15] F. Benamira, J. P. Provost and G. J. Vallée, “Separable
and Non-Separable Spin Glass Models,” Journal de Phy-
sique, Vol. 46, No. 8, 1985, pp. 1269-1275.
doi:10.1051/jphys:019850046080126900
[16] D. Grensing and R. Kühn, “On Classical Spin-Glass
Models,” Journal de Physique, Vol. 48, No. 5, 1987, pp.
713-721. doi:10.1051/jphys:01987004805071300
[17] A. S. Gevorkyan, et al., “New Mathematical Conception
and Computation Algorithm for Study of Quantum 3D
Disordered Spin System under the Influence of External
Field,” Transactions on Computational Science VII, 2010,
pp. 132-153.

A. S. GEVORKYAN ET AL.
497
[18] S. F. Edwards and P. W. Anderson, “Theory of Spin
Glasses,” Journal of Physics F, Vol. 5, 1975, pp. 965-974.
doi:10.1088/0305-4608/5/5/017
[19] A. S. Gevorkyan, H. G. Abajyan and H. S. Sukiasyan,
ArXiv: cond-mat.dis-nn 1010.1623v1.
[20] I. Ibragimov and Y. Linnik, “Independent and Stationary
Sequences of Random Variebles,” Mathematical Reviews,
Vol. 48, 1971, pp. 1287-1730.
[21] C. J. Thompson, “Phase Transitions and Critical Phe-
nomena,” Academic Press, Vol. 1, 1972, pp. 177-226.
[22] E. Bolthausen and A. Bovier, “Spin Glasses,” Springer,
Vol. 163, No. 6, 2007, pp. 1900-2075.