J. Biomedical Science and Engineering, 2011, 4, 479-482 JBiSE
doi:10.4236/jbise.2011.46060 Published Online June 2011 (http://www.SciRP.org/journal/jbise/).
Published Online June 2011 in SciRes. http://www.scirp.org/journal/JBiSE
Phase space in EEG signals of women refferred to meditation
clinic
Ateke Goshvarpour1, Atefeh Goshvarpour1, Saeed Rahati2, Vahid Saadatian3, Minoo Morvarid4
1Department of Biomedical Engineering, Islamic Azad University, Mashhad Branch, Iran;
2Department of Electronic Engineering, Islamic Azad University, Mashhad Branch, Iran;
3Department of Psychology, Islamic Azad University, Mashhad Branch, Iran;
4Headmaster of Meditation Clinic, Mashhad, Iran.
Received 24 December 2010; revised 18 February 2011; accepted 10 May 2011.
ABSTRACT
Poincare plots are commonly used to study the non-
linear behavior of physiological signals. In the time
series analysis, the width of Poincare plots can be
considered as a criterion of short-term variability in
signals. The hypothesis that Poincare plot indexes of
electroencephalogram (EEG) signals can detect dy-
namic changes during meditation was examined in
sixteen healthy women. Therefore, the aim of this
study is to evaluate the effect of different lags on the
width of the Poincare plots in EEG signals during
meditation. Poincare plots with six different lag (1-6)
were constructed for two sets of data and the width of
the Poincare plot for each lag was calculated. The
results show that during meditation the width of
Poincare plots tended to increase as the lag increased.
The Poincare plot is a quantitative visual tool which
can be applied to the analysis of EEG data gathered
over relatively short time periods. The simplicity of
the width of Poincare plot calculation and its' adap-
tation to the chaotic nature of the biological signals
could be useful to evaluate EEG signals during me-
ditation.
Keywords: Electroen cephalogram; Meditation; Poincare
Plots; Nonlinear Dynamics
1. INTRODUCTION
Meditation, a technique that frees the mind from distrac-
tions and allows for communication with the Master
Within, can lead to numerous physical, mental and spi-
ritual benefits. Meditation is a unique state of con-
sciousness with associated changes in the physiological
and psychological functions in the brain. Some research
has shown that meditation characterized by marked re-
ductions in metabolic activity, increased orderliness and
integration of brain functioning, decreased peripheral
vascular resistance, and increased cerebral blood flow. In
addition, meditation produces comprehensive improve-
ments in mental health, enhancing positive features, and
reducing v a rious fo r ms of psychological dist r e ss [ 1].
The electroencephalogram (EEG) signals reflect the
electrical activity of the brain. The study of the brain
electrical activity, through the electroencephalographic
records, is one of the most important tools for the diag-
nosis of neurological diseases. The initial time series
analysis based on statistical indexes was soon replaced
by more sophisticated analysis capable of extracting
more information of the signal.
Since the dynamics of the brain system are chaotic,
nonlinear methods have been applied to the analysis of
EEG signals. One of these techniques is the Poincare
plot. This technique was first used as a qualitative tool
and later, the quantification of the Poincare plot geome-
try was proposed.
In previous studies, Poincare plot is extensively used
for qualitative visualization of heart rate signals. Tulppo
et al. [2] fit an ellipse to the shape of the Poincare plot in
order to calculate heart rate indices. Brennan et al. [3]
demonstrate that the width of the Poincare plot indicates
the level of short-term variability in h eart rate signals. A
number of variations have been proposed, in order to
optimize the use of the Poincare plot as a quantitative
tool [4,5]. One of them is the lagged Poincare plot. The
conventional plot has two dimensions and a lag of one
interval, i.e., each point on the plot consists of a pair of
successive intervals (RRi, RRi+1). Lerma et al. [6] used
longer lags (RRi, RRi+t with 1  t  8) to analyze HRV in
chronic renal failure patients. Contreras et al. [4] showed
that lagged Poincare widths and spectral indices might
be useful to distinguish normal from pathological heart
rate signals. Thakre and Smith [7] used lags from 1 to 10
for heart rate analysis in patients with chronic heart fail-

A. Goshvarpour et al. / J. Biomedical Science and Engineering 4 (2011) 479-482 480
ure.
Other investigators have reported systematic changes
in EEG trajectories associated with the seizure onset [8].
We felt that such changes might also be found in the
EEG during meditation. Because of its sensitivity to the
state of a system, the Poincare trajectory is potentially
valuable for visualizing changes such as the transition
from the normal state to meditation. We decided to ex-
plore Poincare trajectories associated with this transition,
and to describe the changes systematically that were
evident, in the Poincare plots. However mathematical
manipulations of the EEG have failed to give way to
visual inspection as a primary clinical tool. Therefore,
we were interested in the possible value of this visual
tool, which is based on current concepts from nonlinear
dynamic analysis, but has the advantage of providing
detailed information that can be scrutinized by the hu-
man eye. Since these trajectories may provide a new way
to characterize, describe, and quantify EEG dynamics,
we wished to evaluate their possible usefulness in the
specific psycho-physiological state.
The aim of the present study was to evaluate the width
of the Poincare plot with different lags on EEG signals
during meditation. For this purpose, we used the EEG
signals of two groups of subjects (before meditation and
during meditation). Poincare plots with six different lag
(1-6) were constr uc ted and the w idth of th e Poin car e plot
for each lag was calculated.
The outline of this study is as follows. At first, we
briefly describe the sets of the EEG signals used in our
study. Then, we explain the Poincare plot and its' width.
Finally, we present the results of analysis of Poincare
plots with six different lags (1-6), and we conclude the
study.
2. METHOD
2.1. Dat a C ollection
Subjects were considered to be at an advanced level of
meditation training. The sixteen meditators, took part in
the study (women, age range 30 - 53, mean 38.19 years).
The subjects were in good general health and did not
follow any specific heart diseases. The subjects were
asked not to eat salty or fat foods before meditation
practices or data recording. Informed written consent
was obtained from each subject after the experimental
procedures had been explained.
The experimental procedure was divided into two dif-
ferent stages: Subjects were first instructed to sit quietly
for 5 minutes and kept their eyes closed. After that, they
performed meditation. Meditation prescribes a certain
bodily posture. They sit on a cushion 5 to 10 centimeters
thick that is placed on blanket. They cross their legs so
that one foot rests on the opposite thigh with the sole of
their foot turned up and with their knees touching the
blanket (lotus or half-lotus position). The torso should be
kept straight, but it should not be strained. The head
should be kept high with eyes closed. During this session,
the meditators sat quietly, liste ning to the guidance of the
physician and focusing on the breat h .
The meditation EEG signals were recorded in medita-
tion clinic using 16-channel Powerlab (manufactured by
ADInstruments). EEG activity was recorded using three
electrodes (i.e., Fz, Cz and Pz) according to the Interna-
tional 10-20 System, referenced to linked ear lobe elec-
trodes. The monitoring system hardware filters band
passed data in range: 0.1 - 50 Hz for EEG time series. A
digital notch filter was applied to the data at 50 Hz to
remove any artifacts caused by alternating current line
noise. The sampling rate was 400 H z.
2.2. Poincare Plots
Poincare plot is a geometrical representation of a time
series in a Cartesian plane. A two dimensional plot con-
structed by plotting consecutive points is a representa-
tion of time series on phase space or Cartesian plane [5].
A standard Poincare plot of EEG signal is shown in
Figure 1. Two basic descriptors of the plot are SD1 and
SD2. The line of identity is the 45° imaginary diagonal
line on the Poincare plot and the points falling on the
imaginary line has the property Xn = Xn+1. SD1 measures
the dispersion of points perp endicular to th e line of iden-
tity, whereas SD2 measures the dispersion along the line
of identity.
Fundamentally, SD1 and SD2 of Poincare plot is di-
rectly related to the basic statistical measures, standard
deviation of time series (SDX), and standard deviation of
the successive difference of time series (SDSD), which is
given by the relation shown in (1) and (2).

22
110
2XX
SD SDSD



 (1)
 
2
22 2
21
2012
2XX
SD SDXSDSDX    (2)
Where γX(0) and γX(1) is the autocorrelation function for
lag 0 and lag 1 of data intervals and X is the mean of
time series intervals. From (1) and (2), it is clear that the
measures SD1 and SD2 are actually derived from the
correlation and mean of the time series with lag 0 and
lag 1. The above equation sets are derived for unit time
delay Poincare plot. Researchers have shown interest in
plots with different time delays to get a better insight in
the time-series signal. Usually the time delay is multiple
of the cycle length or the sampling time of the signal [3].
The dependency among the variables is controlled by the
choice of time delay, and the most conventional analysis
is performed with higher order linear correlation be-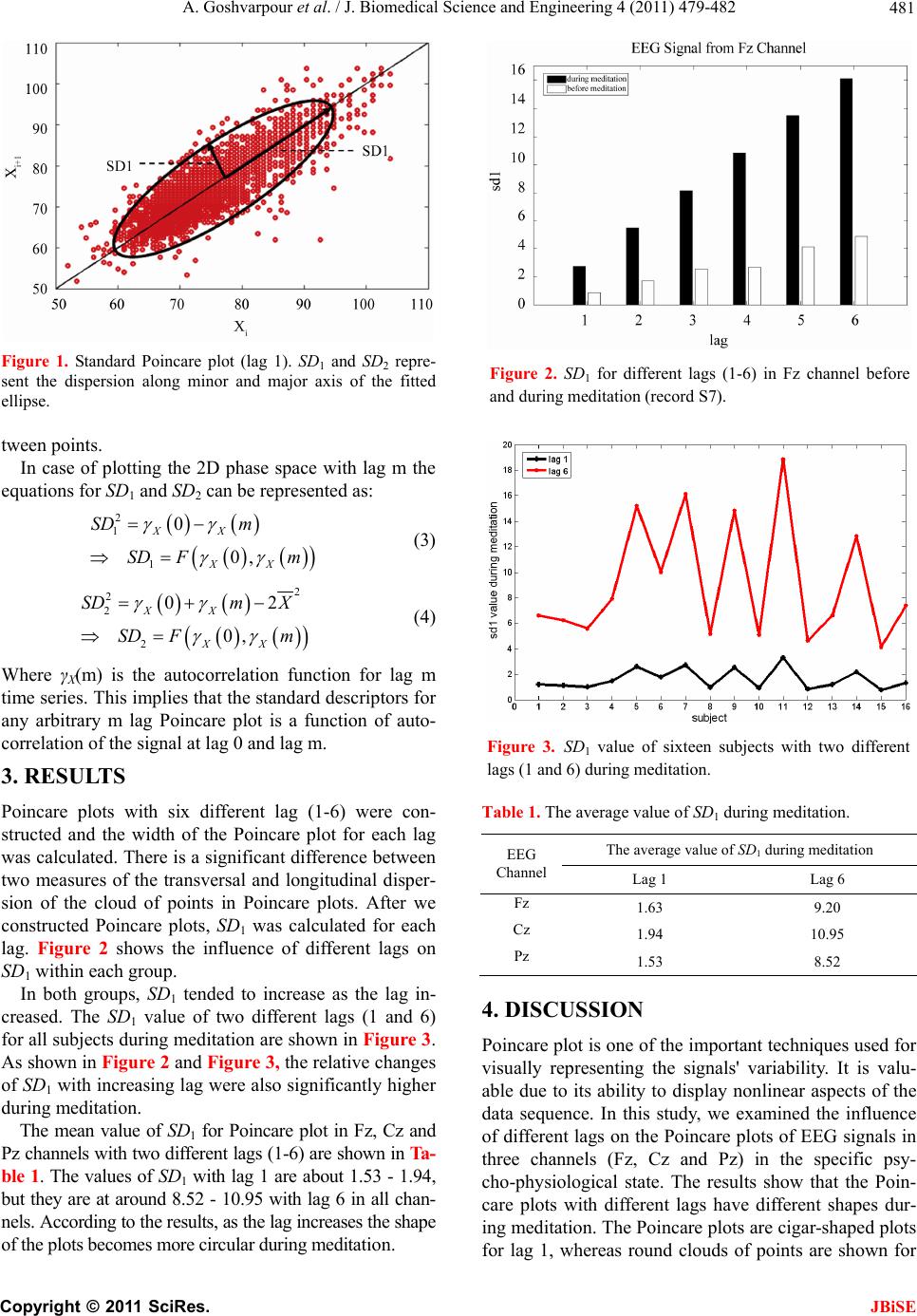

A. Goshvarpour et al. / J. Biomedical Science and Engineering 4 (2011) 479-482 481
Figure 1. Standard Poincare plot (lag 1). SD1 and SD2 repre-
sent the dispersion along minor and major axis of the fitted
ellipse.
tween points.
In case of plotting the 2D phase space with lag m the
equations for SD1 and SD2 can be represented as:



  
2
1
1
0
0,
XX
XX
SD m
SD Fm



 (3)
 
  
2
2
2
2
02
0,
XX
XX
SDm X
SD Fm


 

(4)
Where γX(m) is the autocorrelation function for lag m
time series. This implies that the standard descriptors for
any arbitrary m lag Poincare plot is a function of auto-
correlation of the signal at lag 0 and lag m.
3. RESULTS
Poincare plots with six different lag (1-6) were con-
structed and the width of the Poincare plot for each lag
was calculated. There is a significant difference between
two measures of the transversal and longitudinal disper-
sion of the cloud of points in Poincare plots. After we
constructed Poincare plots, SD1 was calculated for each
lag. Figure 2 shows the influence of different lags on
SD1 within each gro up .
In both groups, SD1 tended to increase as the lag in-
creased. The SD1 value of two different lags (1 and 6)
for all subjects during meditatio n are shown in Figure 3.
As shown in Figure 2 and Figure 3, the relative changes
of SD1 with increasing lag were also significantly higher
during meditation.
The mean value of SD1 for Poincare plot in Fz, Cz and
Pz channels with two different lags (1-6) are shown in Ta-
ble 1. The values of SD1 with lag 1 are about 1.53 - 1.94,
but they are at around 8.52 - 10.95 with lag 6 in all chan-
nels. According to the r esu lts, as th e lag in creases th e shap e
of the plots becomes more circular during meditation.
Figure 2. SD1 for different lags (1-6) in Fz channel before
and during meditation (record S7).
Figure 3. SD1 value of sixteen subjects with two different
lags (1 and 6) during meditation.
Table 1. The average value of SD1 during meditation.
The average value of SD1 during meditation
EEG
Channel Lag 1 Lag 6
Fz 1.63 9.20
Cz 1.94 10.95
Pz 1.53 8.52
4. DISCUSSION
Poincare plot is one of the important techniques used for
visually representing the signals' variability. It is valu-
able due to its ability to display nonlinear aspects of the
data sequence. In this study, we examined the influence
of different lags on the Poincare plots of EEG signals in
three channels (Fz, Cz and Pz) in the specific psy-
cho-physiological state. The results show that the Poin-
care plots with different lags have different shapes dur-
ing meditation. The Poincare plots are cigar-shaped plots
for lag 1, whereas round clouds of points are shown for

A. Goshvarpour et al. / J. Biomedical Science and Engineering 4 (2011) 479-482 482
higher lags. The reason of this change is, when points
are plotted against immediately preceding poin ts (lag 1),
the correlation between these will be increased if they
were more widely separated. Cigar-shaped plots ex-
pressed the high correlation, whereas round clouds of
points are typical of lack of correlation.
On a lag 1 Poincare plot, SD1 measures the variability
from one point of time series to the next. However, when
we consider SD1 from Poincare plots with longer lags,
the term of the variability is ex tended, from one point of
time series to another separated from it by many inter-
vals. The longer the distance between these points, the
higher the mean time interval between the Poincare p lots
points wh i ch are being summari z ed by SD1.
The major advantage of the Poincare plots lies in their
relative insensitivity to artifacts. In ad dition, the simplic-
ity of the width of Poincare plot calculation and its' ad-
aptation to the chaotic nature of the biological signals
could be useful to evaluate EEG signals during medita-
tion.
5. CONCLUSION
In this study, we have shown that SD1 tended to increase
as the lag increased. The rate of changes in SD1 with
increasing lags was also significantly higher during me-
ditation (Figure 2). These changes provide supplemen-
tary information about th e activity of brain.
The comparative dynamic measures of the lagged
Poincare plots give more insight of the EEG signals in a
specific psycho-physiological state. We propose that
these approaches of analysis can be used to improve the
analysis of EEG signals.
Other indices of Poincare plots like the ratio of SD1/
SD2 or asymmetry in the Poincare plot can be studied in
the future. Furthermore, the influence of different lags
on Poincare plots during meditation could be analyzed in
other biological signals like electrocardiogram and res-
piration.
6. ACKNOWLEDGEMENTS
We thank Mrs. Shahla Khoshkholgh for her assistance in collecting the
data that was used in this investigation. The authors would also like to
thank all the subjects for their good collaborations.
REFERENCES
[1] Rubia, K. (2009) The neurobiology of meditation and its
clinical effectiveness in psychiatric disorders. Biological
Psychology, 82, 1-11.
doi:10.1016/j.biopsycho.2009.04.003
[2] Tulppo, M., Makikallio, T.H., Takala, T.E., Seppanen, T.
and Huikuri, H.V. (1996) Quantitative beat-to-beat
analysis of heart rate dynamics during exercise. American
Journal of Physiology, 271, H244-H252.
[3] Brennan, M., Palaniswami, M. and Kamen, P. (2001) Do
existing measures of Poincare plot geometry reflect
nonlinear features of heart rate variability? IEEE Tran-
sactions on Biomedical Engineering, 48, 1342-1347.
doi:10.1109/10.959330
[4] Contreras, P., Canetti, R. and Migliaro, E. (2007)
Correlations between frequency-domain HRV indices
and lagged Poincare plot width in healthy and diabetic
subjects. Physiological Measurment, 28, 85-94.
doi:10.1088/0967-3334/28/1/008
[5] Karmakar, C., Khandoker, A., Gubbi, J. and Palaniswami,
M. (2009) Complex correlation measure: A novel
descriptor for Poincare plot. Bio-Medical Engineering,
13, 8-17.
[6] Lerma, C., Infant, O., Perez-Grovas, H. and Jose, M.
(2003) Poincare plot indexes of heart rate variability
capture dynamic adaptations after haemodialysis in
chronic renal failure patients. Clinical Physiology and
Functional Imaging, 23, 72-80.
doi:10.1046/j.1475-097X.2003.00466.x
[7] Thakre, T. and Smith, M. (2006) Loss of lag-response
curvilinearity of indices of heart rate variability in
congestive heart failure. BMC Cardiovascular Disorders, 6,
27. doi:10.1186/1471-2261-6-27
[8] Collura, T., Morris, H.H., Burgess, R.C., Jacobs, E.C.
and Klem, G.H. (1992) Phase-plane trajectories of EEG
seizure patterns in epilepsy. American Journal of EEG
Technology, 32, 295-307.