J. Biomedical Science and Engineering, 2008, 1, 75-78
Published Online August 2008 in SciRes. http://www.srpublishing.org/journal/jbise JBiSE
A method for retrieving the waveform of the pres-
sure pulsations from the output of an electronic os-
cillometer
K. Razi Naqvi1, Tamas Jávorfi 1 & Camer W. Vellani2
1Department of Physics , Norwegian University of Science an d Technology, N-7491 Trondheim, Norway. 2The Aga Khan University, Stadium Road, P.O. Box
3500, Karachi 74800, Pakistan. Correspondence should be add ressed to K. Razi Na qvi ( [e-mail]).
ABSTRACT
In the most common version of an oscillometric
blood pressure monitor, the output from the
pressure transducer, Y(t), is split into two parts,
and used for separate determinations of the
pressure inside the pneumatic cuff and its fluc-
tuating part; the latter is derived by sending Y(t)
to a high-pass filter (HPF) and amplifying the fil-
tered part to obtain the oscillometric signal O(t).
Using a typical HPF-amplifier combination, we
show that if p(t), the pulsatile part of the cuff
pressure, is defined to be a train of positive-
going pulses, O(t) turns out to be rather close
but not identical to dp/dt, and to demonstrate
that one can easily retrieve p(t) from a record of
O(t). This means that, with a small modification,
the instrument can provide both p(t) and dp/dt;
the practical advantages of this demonstration
are pointed out.
Keywords: Blood pressure, Oscillometry
1. INTRODUCTION
The oscillometric method of measuring blood pressure,
which predates the discovery of the eponymous Korot-
koff sounds, relies on examining only the pulsating part
of the pressure in the pneumatic cuff used for occluding a
suitably sized artery of the subject [1-7]. Even when the
cuff pressure P is higher than the systolic blood pressure
(sbp) and the underlying artery is occluded, the sensor
used for measuring P registers small fluctuations in re-
sponse to the arterial pulse. As the counterpressure ap-
plied through the cuff is slowly reduced from a suprasys-
tolic level to a value lower than the diastolic blood pres-
sure (dbp), or gradually raised from a subdiastolic to a
suprasystolic value, the pressure fluctuations at first in-
crease and then decrease. In the classical, non-electronic
version of the technique, as practised, for example, by
Hill [1] or by Erlanger [2], the operator had direct access,
through the dial of an anaeroid manometer or a graphic
record, to both the pressure signal and the pulsations
(hereafter called p-pulses). The pioneers spent much in-
genuity on finding the physical basis of the phenomenon,
and on establishing criteria for deriving the values of the
sbp, dbp and the mean arterial pressure (map) from the
peak amplitudes of the p-pulses; the activity has come to
be known as oscillometry or oscillotonometry. Though
early variants of the technique, many of which relied on
the use of a double cuff [3,4], failed to displace the aus-
cultatory method, the introduction, a little over thirty
years ago, of inexpensive piezoresistive pressure sensors
[8] gave a new lease of life to oscillometry, and many
commercial devices are now available for automated
measurement of blood pressure.
In most oscillometric monitors, the cuff pressure is
changed in a continuous manner, and it is important to
state at the outset that the following discussion does not
apply to the relatively uncommon design where the coun-
terpressure is varied in a stepwise manner [9, 10]. The
crucial step in the determination of the blood pressure
involves filtering, usually through electronic hardware, in
order to split the signal from the pressure transducer into
a pulsatile part and a background trend of the slow reduc-
tion in the pressure within the cuff. The mode of opera-
tion of a typical electronic oscillometer has been de-
scribed in one publication [5] as follows: “The counter-
pressure signal, monitored via a pressure tap located in
the side of the compression chamber, was filtered using
0.1 Hz high-pass R-C filter to permit separate recording
of the mean counterpressure and amplified pressure oscil-
lations”; similar statements appear in other sources. The
peak amplitudes of the electrical pulses at the output of
the amplifier (hereafter called a-pulses) are used for de-
ducing, with the aid of proprietary algorithms, the values
of sbp, dbp, and map.
With the notable exception of a recent paper by
Amoore [10], practitioners of electronic oscillometry
seem to have paid no attention to the distortion introduced
by the electronic circuitry. Considerations based on the
frequency response of the high-pass filter and the fre-
quency content of the pressure signal lead one to suspect
that an a-pulse would resemble the time derivative of the
corresponding p-pulse. This study was designed to an-
SciRes Copyright © 2008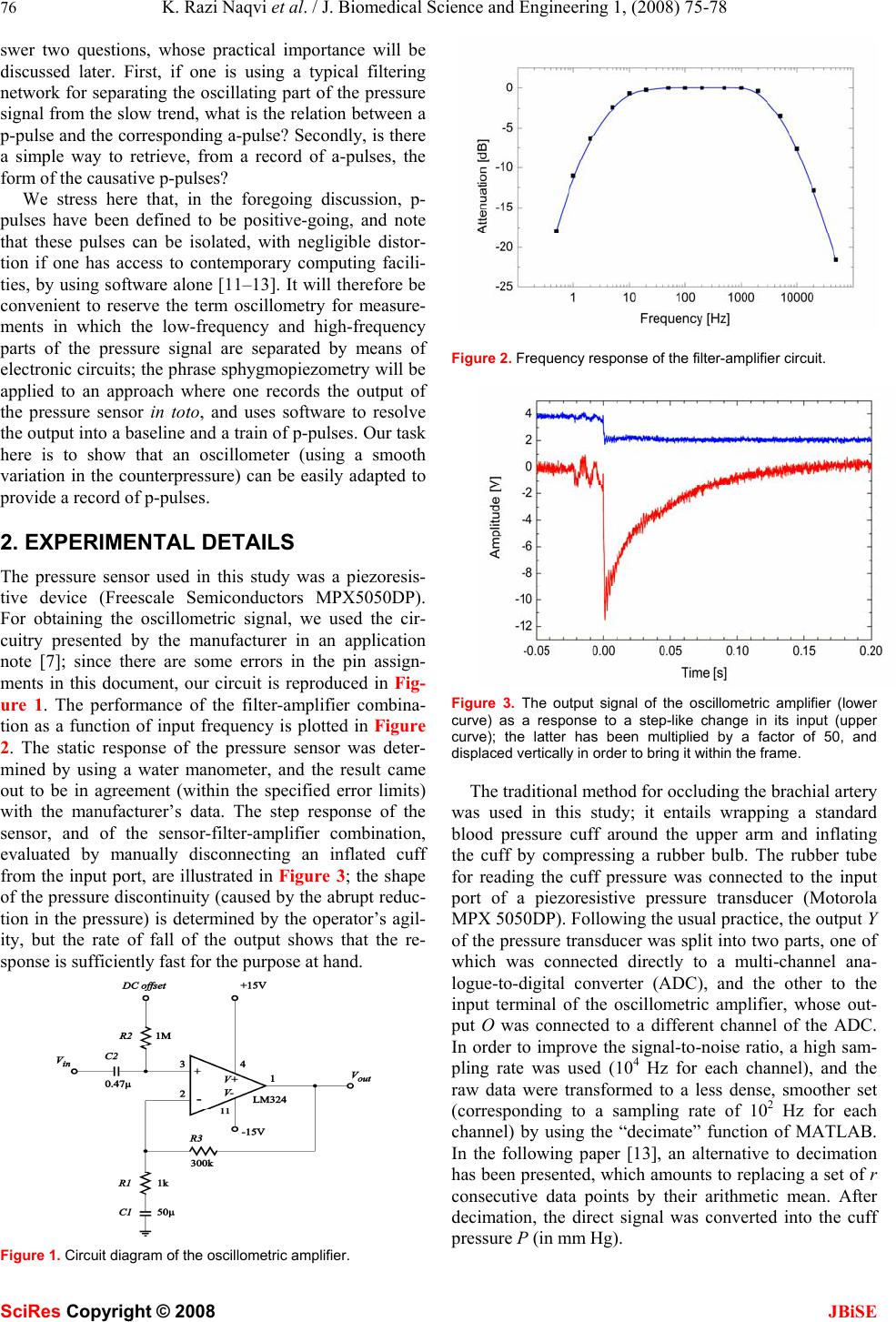

76 K. Razi Naqvi et al. / J. Biomedical Science and Engineering 1, (2008) 75-78
SciRes Copyright © 2008 JBiSE
swer two questions, whose practical importance will be
discussed later. First, if one is using a typical filtering
network for separating the oscillating part of the pressure
signal from the slow trend, what is the relation b etween a
p-pulse and the corresponding a-pulse? Secondly, is there
a simple way to retrieve, from a record of a-pulses, the
form of the causative p-pulses?
We stress here that, in the foregoing discussion, p-
pulses have been defined to be positive-going, and note
that these pulses can be isolated, with negligible distor-
tion if one has access to contemporary computing facili-
ties, by using software alone [11–13]. It will therefore be
convenient to reserve the term oscillometry for measure-
ments in which the low-frequency and high-frequency
parts of the pressure signal are separated by means of
electronic circuits; the phr ase sphygmopiezometry will be
applied to an approach where one records the output of
the pressure sensor in toto, and uses software to resolve
the output into a baseline and a train of p-pulses. Our task
here is to show that an oscillometer (using a smooth
variation in the counterpressure) can be easily adapted to
provide a record of p-pulses.
2. EXPERIMENTAL DETAILS
The pressure sensor used in this study was a piezoresis-
tive device (Freescale Semiconductors MPX5050DP).
For obtaining the oscillometric signal, we used the cir-
cuitry presented by the manufacturer in an application
note [7]; since there are some errors in the pin assign-
ments in this document, our circuit is reproduced in Fig-
ure 1. The performance of the filter-amplifier combina-
tion as a function of input frequency is plotted in Figure
2. The static response of the pressure sensor was deter-
mined by using a water manometer, and the result came
out to be in agreement (within the specified error limits)
with the manufacturer’s data. The step response of the
sensor, and of the sensor-filter-amplifier combination,
evaluated by manually disconnecting an inflated cuff
from the input port, are illustrated in Figure 3; the shape
of the pressure discontinuity (caused by the abrupt reduc-
tion in the pressure) is determined by the operator’s agil-
ity, but the rate of fall of the output shows that the re-
sponse is sufficiently fast for the purpose at hand.
Figure 1. Circuit diagram of the oscillometric amplifier.
Figure 2. Frequency response of the filter-amplifier circuit.
Figure 3. The output signal of the oscillometric amplifier (lower
curve) as a response to a step-like change in its input (upper
curve); the latter has been multiplied by a factor of 50, and
displaced vertically in order to bring it within the frame.
The traditional method for occluding the brachial artery
was used in this study; it entails wrapping a standard
blood pressure cuff around the upper arm and inflating
the cuff by compressing a rubber bulb. The rubber tube
for reading the cuff pressure was connected to the input
port of a piezoresistive pressure transducer (Motorola
MPX 5050DP). Following the usual practice, the output Y
of the pressure transd ucer was split into two parts, one o f
which was connected directly to a multi-channel ana-
logue-to-digital converter (ADC), and the other to the
input terminal of the oscillometric amplifier, whose out-
put O was connected to a different channel of the ADC.
In order to improve the signal-to-noise ratio, a high sam-
pling rate was used (104 Hz for each channel), and the
raw data were transformed to a less dense, smoother set
(corresponding to a sampling rate of 102 Hz for each
channel) by using the “decimate” function of MATLAB.
In the following paper [13], an alternative to decimation
has been presented, which amounts to replacing a set of r
consecutive data points by their arithmetic mean. After
decimation, the direct signal was converted into the cuff
pressure P (in mm Hg).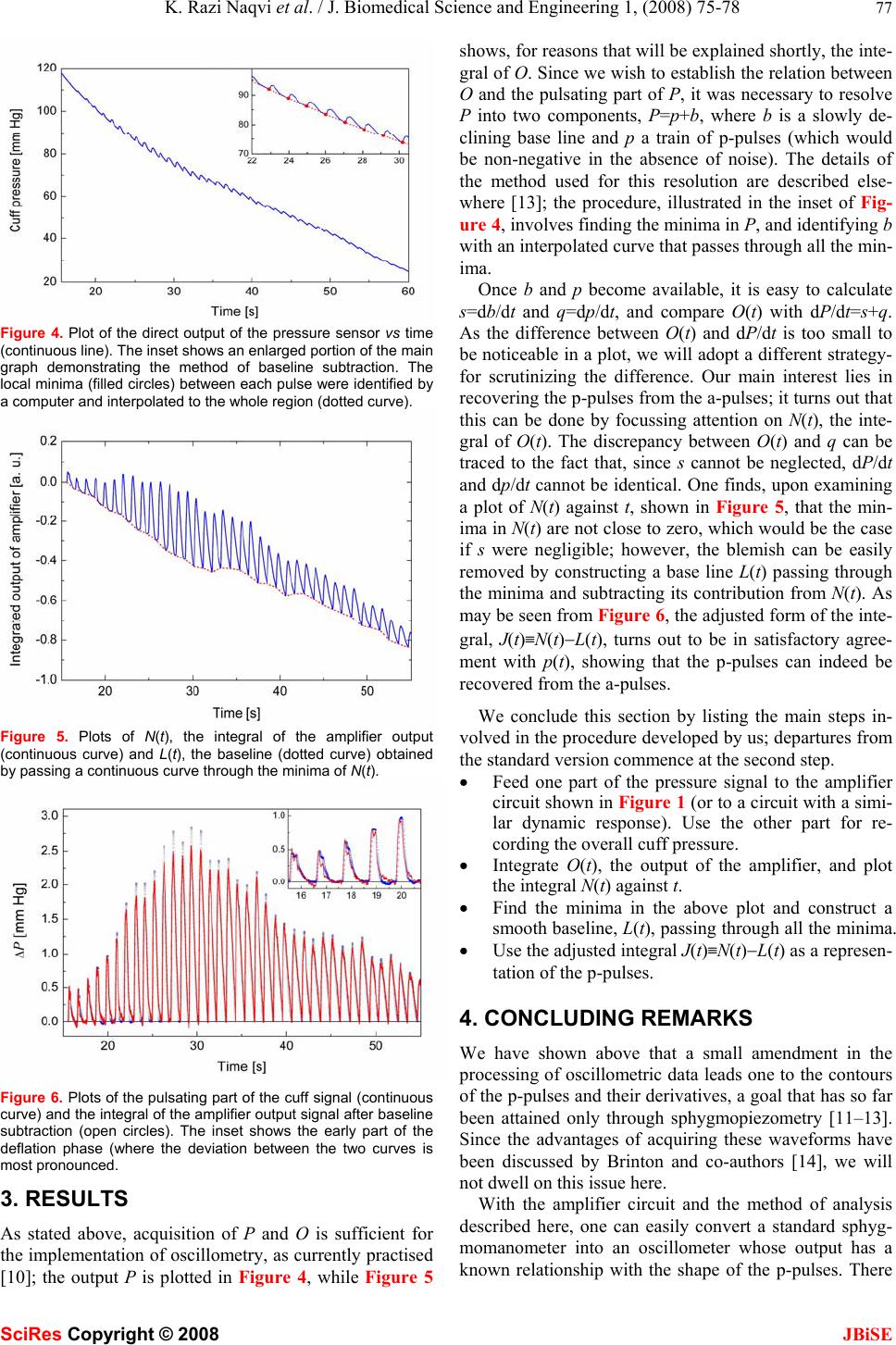

K. Razi Naqvi et al. / J. Biomedical Science and Engineering 1, (2008) 75-78 77
SciRes Copyright © 2008 JBiSE
Figure 4. Plot of the direct output of the pressure sensor vs time
(continuous line). The inset shows an enlarged portion of the main
graph demonstrating the method of baseline subtraction. The
local minima (filled circles) between each pulse were identified by
a computer and interpolated to the whole region (dotted curve).
Figure 5. Plots of N(t), the integral of the amplifier output
(continuous curve) and L(t), the baseline (dotted curve) obtained
by passing a continuous curve through the minima of N(t).
Figure 6. Plots of the pulsating part of the cuff signal (continuous
curve) and the integral of the amplifier output signal after baseline
subtraction (open circles). The inset shows the early part of the
deflation phase (where the deviation between the two curves is
most pronounced.
3. RESULTS
As stated above, acquisition of P and O is sufficient for
the implementation of oscillometry, as curren tly practised
[10]; the output P is plotted in Figure 4, while Figure 5
shows, for reasons th at will be explained sh ortly, the in te-
gral of O. Since we wish to establish the relation between
O and the pulsating part of P, it was necessary to resolve
P into two components, P=p+b, where b is a slowly de-
clining base line and p a train of p-pulses (which would
be non-negative in the absence of noise). The details of
the method used for this resolution are described else-
where [13]; the procedure, illustrated in the inset of Fig-
ure 4, involves finding the minima in P, and identifying b
with an interpolated curve that passes through all the min-
ima.
Once b and p become available, it is easy to calculate
s=db/dt and q=dp/dt, and compare O(t) with dP/dt=s+q.
As the difference between O(t) and dP/dt is too small to
be noticeable in a plot, we will adopt a different strategy-
for scrutinizing the difference. Our main interest lies in
recovering the p-pulses from the a-pulses; it turns out that
this can be done by focussing attention on N(t), the inte-
gral of O(t). The discrepancy between O(t) and q can be
traced to the fact that, since s cannot be neglected, dP/dt
and dp/dt cannot be identical. One finds, upon examining
a plot of N(t) against t, shown in Figure 5, that the min-
ima in N(t) are not close to zero, which would be the case
if s were negligible; however, the blemish can be easily
removed by constructing a base line L(t) passing through
the minima and subtracting its contribution from N(t). As
may b e s e en f ro m Figure 6, the adjusted form of the inte-
gral, J(t)≡N(t)−L(t), turns out to be in satisfactory agree-
ment with p(t), showing that the p-pulses can indeed be
recovered from the a-pulses.
We conclude this section by listing the main steps in-
volved in the procedure developed by us; departures from
the standard version commence at the second step.
• Feed one part of the pressure signal to the amplifier
circuit shown in Figure 1 (or to a circuit with a simi-
lar dynamic response). Use the other part for re-
cording the overall cuff pressure.
• Integrate O(t), the output of the amplifier, and plot
the integral N(t) against t.
• Find the minima in the above plot and construct a
smooth baseline, L(t), passing through all the minima.
• Use the adjusted integral J(t)≡N(t)−L(t) as a represen-
tation of the p-pulses.
4. CONCLUDING REMARKS
We have shown above that a small amendment in the
processing of o scillometric data leads one to th e contours
of the p-pulses and their derivatives, a goal that has so far
been attained only through sphygmopiezometry [11–13].
Since the advantages of acquiring these waveforms have
been discussed by Brinton and co-authors [14], we will
not dwell on this issue here.
With the amplifier circuit and the method of analysis
described here, one can easily convert a standard sphyg-
momanometer into an oscillometer whose output has a
known relationship with the shape of the p-pulses. There

78 K. Razi Naqvi et al. / J. Biomedical Science and Engineering 1, (2008) 75-78
SciRes Copyright © 2008 JBiSE
is at least one commercial instrument that allows the user
to record both P and O [10]. This means that the time is
now ripe for establishing reliable and device-independent
criteria for deducing sbp and dbp from oscillometric data.
We conclude by drawing attention to another point of
practical importance. The amplifier circuit used in this
study follows the approach chosen by previous oscil-
lometrists, but the data presented here indicate that an
appropriately designed operational differentiator would
perform equally well; if the cuff deflation (or inflation) is
arranged to be a linear ramp [11, 12], dP/dt and dp/dt
would differ only by a constant, making the task of base-
line correction a trivial matter.
REFERENCES
[1] Hill, L. (1898) On rest, sleep, and work and the concomitant
changes in the circulation of the blood. Lancet, 151, 282–285.
[2] Erlanger, J. (1916) Studies in blood pressure estimations by
indirect methods: I. The mechanism of the oscillatory criteria. Am.
J. Physiol., 39, 401–446.
[3] Burch, G.E. and DePasquale, N.P. (1962) Primer of Clinical
Measurement of Blood Pressure, C. V. Mosby Ed. St. Louis CO
1962, 15−36.
[4] Corall, I.M. and Strunin, L. (1975) Assessment of the Von
Recklinghausen oscillotonometer. Anaesthesia, 30, 59–66.
[5] Mauck, G.W., Smith, C.R., Geddes, L.A. and Bourland, J.D. (1980)
Meaning of the point of maximum oscillations in cuff pressure in
the indirect measurement of blood-pressure⎯Part II. Trans ASME,
102, 28–33.
[6] Geddes, L.A., Voelz, M., Combs, C., Reiner D. and Babbs, C.F.
(1982) Characterization of the oscillometric method for measuring
indirect blood-pressure. Ann. Biomed. Eng., 10, 271–280.
[7] Chua, C.S. and Hin, S.M. (2005) Digital blood pressure meter.
Freescale Semiconductor, (http://www.freescale.com/files/sensors/
doc/app_note/AN1571.pdf.)
[8] Middelhoek, S. and Noorlag, D.J.W. (1981) Silicon micro-
transducers. J. Phys. E: Sci. Instrum., 14, 1343–1352.
[9] Silas, J.H., Barker, A.T. and Ramsay, L.E. (1980) Clinical-
evaluation of dinamap-845 automated blood-pressure recorder. Br.
Heart J., 43, 202–205.
[10] Amoore, J.N. (2006) Extracting oscillometric pulses from the cuff
pressure: does it affect the pressure determined by oscillometric
blood pressure monitors? Blood P r ess. Monit., 11, 269–279.
[11] Baker, P.D., Orr, J.A., Westenskow, D.R. and Egbert, T.P. Method
for determining blood pressure utilizing a neural network. U.S.
Patent 5,339,818, A u g u s t 2 3 , 1994.
[12] Jazbinsek, V., Luznik, J. and Trontelj, Z. (2005) Non-invasive
blood pressure measurements: separation of the arterial pressure
oscillometric waveform from the deflation using digital filtering.
IFBME proceedings of EMBEC’05, (http://fizika.imfm.si/
jazbinsek/konf2005/2268F.pdf)
[13] Naqvi, K.R., Parigi, L., Vellani, C.W. and Kumar, S. (2008)
Noninvasive method for determining blood pressure and contours
of arterial and volume pulses. JBiSE,1,79-84.
[14] Brinton, T.J., Cotter, B., Kailasam, M.T., Brown, D.L., Chio, S.,
O’Connor, D.T. and DeMaria, A.N. (1997) Development and
validation of a noninvasive method to determine arterial pressure
and vascular compliance. Am. J. Cardiol., 80, 323–330.