Journal of Applied Mathematics and Physics
Vol.03 No.04(2015), Article ID:55824,6 pages
10.4236/jamp.2015.34056
Dirac Coupled Channel Analyses of Proton Inelastic Scatterings from s-d Shell Nuclei
Sugie Shim*, Moon-Won Kim, Young-You Kim
Physics Department, Kongju National University, Gonjusi, Republic of Korea
Email: *shim@kongju.ac.kr


Received February 2015

ABSTRACT
Proton inelastic scatterings from several s-d shell nuclei are analyzed using optical potential model and collective model in Dirac coupled channel formalism. The optical potential parameters obtained phenomenologically for the scatterings from the s-d shell nuclei are compared with each other for systematic Dirac analysis. Dirac equations are reduced to the second-order differential equations in order to obtain the Schroedinger equivalent effective central and spin-orbit optical potentials, and the surface-peaked phenomena are observed at the real effective central potentials for the scatterings from 22Ne, 20Ne and 24Mg. By analyzing the obtained effective spin-orbit potentials, it is confirmed that the spin-orbit interaction is a surface-peaked interaction. The first-order rotational collective models are used to describe the low-lying excited states of the ground state rotational bands in the s-d shell deformed nuclei, and the obtained deformation parameters are analyzed by comparing with each other, and compared with those obtained by using the nonrelativistic calculations. The obtained deformation parameters of Dirac phenomenological calculations for the s-d shell nuclei are found to agree pretty well with those of the nonrelativistic calculations using the same Woods-Saxon potential shape, even though the theoretical bases are quite different.
Keywords:
Dirac Coupled Channel Analyses, Optical Potential Model, Proton Inelastic Scattering, Collective Model

1. Introduction
Relativistic approaches based on the Dirac equation as the relevant wave equation have been remarkably successful in treating nuclear structure and nuclear reactions. While complete relativistic descriptions of nuclear matter and finite nuclei using a relativistic quantum field theory are absent, considerable progress has been made by using approximate descriptions [1]-[3]. Because Dirac analysis of intermediate energy proton-nucleus elastic scatterings have proven to be very successful for the spherically symmetric nuclei and a few deformed nuclei [3]-[6], the relativistic approaches have been expanded to the inelastic scatterings and have shown considerable improvements compared to the conventional nonrelativistic approaches [7]-[9]. It should be noted that one of the merits of the relativistic approach based on the Dirac equation instead of using the nonrelativistic approach based on the Schroedinger equation is that the spin-orbit potential appears naturally in the Dirac approach when the Dirac equation is reduced to a Schroedinger-like second-order differential equation, whereas the spin-orbit potentials should be inserted by hand in the conventional nonrelativistic Schroedinger approach.
In this work we performed a relativistic Dirac phenomenological coupled channel analyses for the inelastic proton scatterings from several s-d shell nuclei such as 20Ne, 22Ne, 24Mg and 26Mg, systematically. The optical potential model [3] and the first order collective model are used in the calculation. The scalar-vector (S-V) model for the optical potentials is employed, where only Lorentz-covariant scalar and time-like vector potentials are included in the calculation. Woods-Saxon shape is used for the geometry of the optical potentials. The first order rotational collective model is employed in order to describe the collective motion of the low-lying excited states of the ground state rotational bands in the nuclei. The complicated Dirac coupled channel equations are solved numerically to calculate the differential cross-sections by using a computer program called ECIS [10], which employs the sequential iteration method. The Dirac equations are reduced to the Schroedinger-like second-order differential equations by considering the upper component of the Dirac wave function in order to obtain the effective central and spin-orbit optical potentials and the obtained effective potentials for the s-d shell nuclei are analyzed by comparing with each other. The calculated results for the deformation parameters for the low-lying excited states of the ground state rotational band in the s-d shell nuclei are analyzed and compared with those obtained using the nonrelativistic calculations.
2. Theory and Results
Dirac coupled channel analyses are performed phenomenologically for the 800 MeV proton inelastic scatterings from several s-d shell nuclei such as 20Ne, 22Ne, 24Mg and 26Mg, using the optical potential model and the first order collective rotational model. Because the s-d shell nuclei considered in this calculation are spin-0 nuclei, only scalar, time-like vector and tensor optical potentials survive [1] [11], as in spherically symmetric nuclei [12]; hence, the relevant Dirac equation for the proton elastic scattering from the nucleus is given as
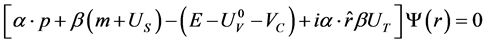 (1)
(1)
Here,  is a scalar potential,
is a scalar potential, 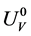 is a time-like vector potential,
is a time-like vector potential, 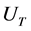 is a tensor potential, and
is a tensor potential, and 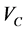 is the Coulomb potential. The scalar and the time-like vector potentials are used as direct potentials in the calculation. Tensor potentials are always present due to the interaction of the anomalous magnetic moment of the projectile with the charge distribution of the target. However, because tensor potentials have been found to be always very small compared to scalar or vector potentials [8], they are neglected in this calculation. The scalar and time-like vector optical potentials are complex and it is assumed that these potentials have Fermi distribution as they are assumed to follow the distribution of nuclear density. Fermi model form factor of Woods-Saxon shape is used for the geometry of the Dirac optical potentials. In the first order rotational model of ECIS, the deformation of the radius of the optical potential is given using the Legendre polynomial expansion method;
is the Coulomb potential. The scalar and the time-like vector potentials are used as direct potentials in the calculation. Tensor potentials are always present due to the interaction of the anomalous magnetic moment of the projectile with the charge distribution of the target. However, because tensor potentials have been found to be always very small compared to scalar or vector potentials [8], they are neglected in this calculation. The scalar and time-like vector optical potentials are complex and it is assumed that these potentials have Fermi distribution as they are assumed to follow the distribution of nuclear density. Fermi model form factor of Woods-Saxon shape is used for the geometry of the Dirac optical potentials. In the first order rotational model of ECIS, the deformation of the radius of the optical potential is given using the Legendre polynomial expansion method;
 (2)
(2)
with 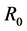 being the radius at equilibrium,
being the radius at equilibrium, 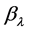 a deformation parameter and
a deformation parameter and 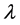 the multipolarity. It is assumed that the shape of the deformed transition potentials follows the shape of the deformed nuclear densities and that the transition potentials can be obtained by assuming that they are proportional to the first-order derivatives of the diagonal potentials. However, it is true that pseudo-scalar and axial-vector potentials may also be present in the equation when we consider inelastic scattering, depending on the model assumed. In the collective model approach used in this work, we assume that we can obtain appropriate transition potentials by deforming the direct potentials that describe the elastic channel fairly well [12]. In order to compare the calculated results with those of the previous nonrelativistic calculations, we reduce the Dirac equation to a Schroedinger-like second- order differential equation by considering the upper component of the Dirac wave function to obtain the effective central and spin-orbit optical potentials [4]. The experimental data for the differential cross sections are obtained from [13]-[15] for the 800 MeV unpolarized proton inelastic scatterings from the s-d shell nuclei, 20Ne, 22Ne, 24Mg and 26Mg.
the multipolarity. It is assumed that the shape of the deformed transition potentials follows the shape of the deformed nuclear densities and that the transition potentials can be obtained by assuming that they are proportional to the first-order derivatives of the diagonal potentials. However, it is true that pseudo-scalar and axial-vector potentials may also be present in the equation when we consider inelastic scattering, depending on the model assumed. In the collective model approach used in this work, we assume that we can obtain appropriate transition potentials by deforming the direct potentials that describe the elastic channel fairly well [12]. In order to compare the calculated results with those of the previous nonrelativistic calculations, we reduce the Dirac equation to a Schroedinger-like second- order differential equation by considering the upper component of the Dirac wave function to obtain the effective central and spin-orbit optical potentials [4]. The experimental data for the differential cross sections are obtained from [13]-[15] for the 800 MeV unpolarized proton inelastic scatterings from the s-d shell nuclei, 20Ne, 22Ne, 24Mg and 26Mg.
Firstly, the 12 parameters of the diagonal scalar and vector potentials in Woods-Saxon shapes are determined numerically to reproduce the experimental elastic scattering differential cross section data by using a sequential iteration method. The observable elastic experimental data are found to be reproduced quite well as shown in our previous publications [8] [9] [16] [17]. The Dirac equations are phenomenologically solved to obtain the best fitting optical potential parameters to the experimental data by using the minimum chi-square 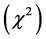 method. The calculated optical potential parameters of the Woods-Saxon shape for the 800 MeV proton elastic scatterings from the s-d shell nuclei are compared in Table 1 [8] [9] [16] [17]. We observe that the real parts of the scalar potentials and the imaginary parts of the vector potentials turn out to be large and negative, and that the imaginary parts of the scalar potentials and the real parts of the vector potentials turn out to be large and positive for all of the considered s-d shell nuclei, showing the same pattern as in the spherically symmetric nuclei [4] [5]. The potential strengths of 22Ne are found to be smaller than those of 20Ne except in scalar imaginary potential, and the potential radii of 22Ne are found to be larger than those of 20Ne in all the potentials. Similarly, the potential strengths of 26Mg are found to be smaller than those of 24Mg in all the potentials, and the potential radii of 26Mg are found to be larger than those of 24Mg except in scalar imaginary potential. The diffusiveness parameters of 22Ne are found to be smaller than those of 20Ne except in scalar real potential, and those of 26Mg are found to be smaller than those of 24Mg in all the potentials.
method. The calculated optical potential parameters of the Woods-Saxon shape for the 800 MeV proton elastic scatterings from the s-d shell nuclei are compared in Table 1 [8] [9] [16] [17]. We observe that the real parts of the scalar potentials and the imaginary parts of the vector potentials turn out to be large and negative, and that the imaginary parts of the scalar potentials and the real parts of the vector potentials turn out to be large and positive for all of the considered s-d shell nuclei, showing the same pattern as in the spherically symmetric nuclei [4] [5]. The potential strengths of 22Ne are found to be smaller than those of 20Ne except in scalar imaginary potential, and the potential radii of 22Ne are found to be larger than those of 20Ne in all the potentials. Similarly, the potential strengths of 26Mg are found to be smaller than those of 24Mg in all the potentials, and the potential radii of 26Mg are found to be larger than those of 24Mg except in scalar imaginary potential. The diffusiveness parameters of 22Ne are found to be smaller than those of 20Ne except in scalar real potential, and those of 26Mg are found to be smaller than those of 24Mg in all the potentials.
In Figure 1, we compared the effective central and spin-orbit potentials of the several s-d shell nuclei. Surface-peaked phenomena are clearly observed for the real parts of the effective central potentials (CR) at 22Ne. The same surface-peaked phenomena are shown at the scatterings from other s-d shell nuclei such as 20Ne and 24Mg, even though they are less clearly shown. The potential strength for the imaginary central potential turned out to be negative, about −20 MeV, at the center of the nucleus 22Ne, while those of other s-d shell nuclei have positive values and that of nonrelativistic calculations was 46.2 MeV [15]. However, the imaginary central potential strength at the surface area is observed to be positive as shown in the figure. It is shown that the potential strength at the surface is important in the phenomenological calculations for the proton scatterings in the previous publication [18]. The surface-peaked phenomena are clearly shown at the effective spin-orbit potentials, and the effective spin-orbit potential strengths turned out to be about the same order with those obtained from nonrelativistic calculations [13]-[15]. It should be noted that the surface-peaked phenomena never appear at the conventional nonrelativistic approaches because they use the Woods-Saxon shapes for both the central and
Table 1. Calculated phenomenological optical potential parameters using Woods-Saxon shape for 800 MeV proton elastic scatterings from several s-d shell nuclei.
Figure 1. Comparison of the effective central and spin-orbit potentials of several s- d shell nuclei. CR and CI represent central real and imaginary potentials, and SOR and SOI represent spin-orbit real and imaginary optical potentials, respectively.
spin-orbit potentials. It is observed that the peak position is shifted to the direction of large r for the nuclei with larger atomic number for both the real (SOR) and the imaginary (SOI) spin-orbit potentials, indicating that the spin-orbit interaction is a surface-peaked interaction. It is noted that one of the merits of the relativistic approach based on the Dirac equation instead of using the nonrelativistic approach based on the Schroedinger equation is that the spin-orbit potential appears naturally in the Dirac approach when the Dirac equation is reduced to a Schroedinger-like second-order differential equation, while the spin-orbit potential should be inserted by hand in the conventional nonrelativistic Schroedinger approach.
Next, eight-parameter searches are performed by including the low-lying excited states of the ground state rotational band, the 2+ and the 4+ states, in addition to the ground state, starting from the 12 parameters for the direct optical potentials obtained in the elastic scattering calculations. Here, the eight parameters are the two deformation parameters, 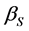 and
and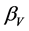 , per each excited state by assuming the real and imaginary deformation parameters are the same for each excited state, and the four potential strengths; the scalar real and imaginary potential strengths and the vector real and imaginary potential strengths, keeping the potential geometries unchanged. The optical potential strengths obtained by fitting the elastic scattering data in the elastic scattering calculation are varied because the channel coupling of the excited states to the ground state should be included in the inelastic scattering calculation. The results of the coupled channel calculations for the differential cross- sections of the excited states in the ground state rotational band are shown in the figures of our previous publications [8] [9] [16] [17] and it is shown that relativistic Dirac coupled channel calculation using an optical potential model could describe the low-lying excited states of the ground state rotational band for 800 MeV unpolarized proton inelastic scatterings from the s-d shell nuclei reasonably well.
, per each excited state by assuming the real and imaginary deformation parameters are the same for each excited state, and the four potential strengths; the scalar real and imaginary potential strengths and the vector real and imaginary potential strengths, keeping the potential geometries unchanged. The optical potential strengths obtained by fitting the elastic scattering data in the elastic scattering calculation are varied because the channel coupling of the excited states to the ground state should be included in the inelastic scattering calculation. The results of the coupled channel calculations for the differential cross- sections of the excited states in the ground state rotational band are shown in the figures of our previous publications [8] [9] [16] [17] and it is shown that relativistic Dirac coupled channel calculation using an optical potential model could describe the low-lying excited states of the ground state rotational band for 800 MeV unpolarized proton inelastic scatterings from the s-d shell nuclei reasonably well.
In Table 2, we show the deformation parameters for the 2+ and the 4+ excited states of the s-d shell nuclei; 20Ne, 22Ne, 24Mg and 26Mg. The deformation parameters for the excited states of 22Ne are shown to be smaller than those of 20Ne, even though the excitation energies for the 2+ and the 4+ states are smaller for 22Ne. Hence, we can say that the couplings of the 2+ and 4+ states to the ground state are weaker for 22Ne than they are for 20Ne. Similarly, the deformation parameters for the 2+ state of the 26Mg are found to be smaller than those of 24Mg, even though the excitation energy for the state is larger for 26Mg in this case. However, the deformation parameters for the 4+ state of 26Mg are shown to be larger than those of 24Mg. Hence, we can say that the couplings of the 2+ state to the ground state are weaker for 26Mg than they are for 24Mg and the couplings of the 4+ state to the ground state are stronger for 26Mg than they are for 24Mg. It is observed that the deformation parameters for the 2+ states are larger than those for the 4+ states in all four s-d shell nuclei, indicating that the
Table 2. Comparison of the deformation parameters for the 2+ and the 4+ excited states for 800 MeV proton scatterings from several s-d shell nuclei.
couplings of the ground states to the 2+ states are stronger than those to the 4+ states in the nuclei. The deformation parameters obtained using the Dirac coupled channel calculations are also compared with those obtained by using the nonrelativistic calculations [13]-[15] [19]. Even though the theoretical bases are quite different, the results of Dirac phenomenological coupled channel calculation for the 2+ and 4+ state excitations of the s-d shell nuclei show pretty good agreement with the results of the nonrelativistic calculation using the same Woods- Saxon potential shape for the geometries of the optical potentials.
3. Conclusion
Relativistic Dirac coupled channel analyses using an optical potential model are performed for the 800 MeV proton inelastic scatterings from several s-d shell nuclei such as 20Ne, 22Ne, 24Mg and 26Mg. The optical potential parameters for the s-d shell nuclei are obtained phenomenologically using scalar-vector potential model and compared with each other for systematic Dirac analysis. The potential strengths of 22Ne are found to be smaller than those of 20Ne except in scalar imaginary potential, and the potential radii of 22Ne are larger than those of 20Ne in all the potentials. Similarly, the potential strengths of 26Mg are found to be smaller than those of 24Mg in all the potentials, and the potential radii of 26Mg are larger than those of 24Mg except in scalar imaginary potential. The diffusiveness parameters of 22Ne are found to be smaller than those of 20Ne except in scalar real potential and those of 26Mg are found to be smaller than those of 24Mg in all the potentials. The effective central and spin-orbit potentials are obtained by reducing Dirac equations to the Schroedinger-like second-order differential equations, and the surface-peaked phenomena are observed at the real effective central potentials for the scattering from 22Ne, as shown in the cases of 20Ne and 24Mg. It is found that the peak position is shifted to the direction of large r for the nuclei with larger atomic number for the spin-orbit potentials, indicating that the spin-orbit interaction is a surface-peaked interaction. The first-order rotational collective models are used to describe the low-lying excited states of the ground state rotational bands in the nuclei, and the obtained deformation parameters are analyzed. Even though the excitation energies for the 2+ and the 4+ states are smaller for 22Ne, the deformation parameters for the excited states of 22Ne are shown to be smaller than those of 20Ne, indicating that the couplings of the 2+ and 4+ states to the ground state are weaker for 22Ne than they are for 20Ne. Similarly, we can say that the couplings of the 2+ state to the ground state are weaker for 26Mg than they are for 24Mg because the deformation parameters for the 2+ state of the 26Mg are found to be smaller than those of 24Mg. The deformation parameters for the 2+ and the 4+ excited states of the ground state rotational band are also compared with those of nonrelativistic calculations, and the deformation parameters obtained in the Dirac phenomenological calculations for the s-d shell nuclei are found to agree pretty well with those of the nonrelativistic calculations using the same Woods-Saxon potential shape, even though the theoretical bases are quite different.
Acknowledgements
This work was supported by a research grant from Kongju National University in 2014.
Cite this paper
Sugie Shim,Moon-Won Kim,Young-You Kim, (2015) Dirac Coupled Channel Analyses of Proton Inelastic Scatterings from s-d Shell Nuclei. Journal of Applied Mathematics and Physics,03,443-448. doi: 10.4236/jamp.2015.34056
References
- 1. Horowitz, C.J. and Serot, B.D. (1981) Self-Consistent Hartree Description of Finite Nuclei in a Relativistic Quantum Field Theory. Nuclear Physics A, 368, 503-528. http://dx.doi.org/10.1016/0375-9474(81)90770-3
- 2. Celenza, L.S. and Shakin, C.M. (1986) Relativistic Nuclear Physics. World Scientific, New-York.
- 3. Arnold, L.G., Clark, B.C., Mercer, R.L. and Swandt, P. (1981) Dirac Optical Model Analysis of p? 40Ca Elastic Scattering at 180 MeV and the Wine-Bottle-Bottom Shape. Physical Review C, 23, 1949-1959.�
- 4. Shim, S. (1989) Relativistic Analyses of Nucle-on-Nucleus Inelastic Scatterings. Ph.D. Thesis, The Ohio State University, USA.
- 5. Kurth, L., Clark, B.C., Cooper, E.D., Hama, S., Shim, S., Mercer, R.L., Ray, L. and Hoffmann, G.W. (1994) Dirac Coupled Channel Calculations for Proton Inelastic Scattering from Spherically Symmetric Nuclei for Projectile Energies of 362,500, and 800 MeV. Physical Review C, 49, 2086-2103. http://dx.doi.org/10.1103/PhysRevC.49.2086
- 6. Shim, S., Clark, B.C., Cooper, E.D., Hama, S., Mercer, R.L., Ray, L., Raynal, J. and Sherif, H.S. (1990) Comparison of Relativistic and Nonrelativistic Approaches to the Collective Model Treatment of p+ 40Ca Inelastic Scattering. Physical Review C, 42, 1592-1597. http://dx.doi.org/10.1103/PhysRevC.42.1592
- 7. Kelly, J.J. (2005) Relativistic Distorted-Wave Impulse Approximation Analysis of 12C(e,e’p) for Q2 < 2?(GeV/c)2. Physical Review C, 71, 064610.1-064610.5.�
- 8. Shim, S., Kim, M.W., Clark, B.C. and Kurth Kerr, L. (1999) Dirac Coupled Channel Analyses of 800 MeV Proton Inelastic Scattering from 24Mg. Physical Review C, 59, 317-322. http://dx.doi.org/10.1103/PhysRevC.59.317
- 9. Shim, S. and Kim, M.W. (2012) Systematic Dirac Analyses of Proton Inelastic Scatterings from Axially Symmetric Deformed Nuclei. International Journal of Modern Physics E, 21, 1250098.1-1250098.10.
- 10. Raynal, J. (1994) Computing as a Language of Physics. ICTP International Seminar Course, IAEA, Italy, 281. Raynal, J. (1972) Notes on ECIS94, Note CEA-N-2772.
- 11. Furnstahl, R.J., Price, C.E. and Walker, G.E. (1987) Systematics of Light Deformed Nuclei in Relativistic Mean-Field Models. Physical Review C, 36, 2590-2600. http://dx.doi.org/10.1103/PhysRevC.36.2590
- 12. Ray, L. and Hoffmann, G.W. (1986) Relativistic and Nonrelativistic Impulse Approximation Descriptions of 300 - 1000 MeV Proton + Nucleus Elastic Scattering. Physical Review C, 31, 538-560. http://dx.doi.org/10.1103/PhysRevC.31.538
- 13. Blanpied, G.S., Balchin, G.A., Langston, G.E., Ritchie, B.G., Barlett, M.L., Hoffmann, G.W., McGill, J.A., Franey, M.A., Gazzaly, M. and Wildenthal, B.H. (1984) Excitation of the Ground State Rotational Band in 20Ne by 0.8 GeV Protons. Physical Review C, 30, 1233-1237. http://dx.doi.org/10.1103/PhysRevC.30.1233
- 14. Blanpied, G.S., Ritchie, B.G., Barlett, M.L., Fergerson, R.W., Hoffmann, G.W., McGill, J.A. and Wildenthal, B.H. (1988) Elastic and Inelastic Scattering of 0.8 GeV Polarized Protons from 24Mg and 26Mg. Physical Review C, 37, 1987-1999. http://dx.doi.org/10.1103/PhysRevC.37.1987
- 15. Blanpied, G.S., Ritchie, B.G., Barlett, M.L., Fergerson, R.W., Hoffmann, G.W., McGill, J.A. and Wildenthal, B.H. (1988) Elastic and Inelastic Scattering of 0.8 GeV Polarized Protons from 20Ne and 22Ne. Physical Review C, 38, 2180-2186. http://dx.doi.org/10.1103/PhysRevC.38.2180
- 16. Kim, M.W. and Shim, S. (2015) Dirac Phenomenological Analyses of Unpolarized Proton Inelastic Scattering from 22Ne. Journal of the Korean Physical Society, 66, 850-854. http://dx.doi.org/10.3938/jkps.66.850
- 17. Shim, S. and Kim, M.W. (2014) Dirac Analyses of Proton Inelastic Scatterings from an s-d Shell Nucleus 20Ne. Journal of the Korean Physical Society, 64, 483-487. http://dx.doi.org/10.3938/jkps.64.483
- 18. Barlett, M.L., McGill, J.A., Ray, L., Barlett, M.M., Hoffmann, G.W., Hintz, N.M., Kyle, G.S., Franey, M.A. and Blanpied, G.S. (1980) Proton Scattering from 154Sm and 176Yb at 0.8 GeV. Physical Review C, 22, 1168-1179. http://dx.doi.org/10.1103/PhysRevC.22.1168
- 19. de Swiniarski, R., Bacher, A.D., Resmini, F.G., Plattner, G.R., Hendrie, D.L. and Raynal, J. (1972) Determination of Deformation Parameters of 20Ne and 22Ne by Inelastic Scattering of Polarized Protons. Physical Review Letters, 28, 1139-1142. http://dx.doi.org/10.1103/PhysRevLett.28.1139
NOTES

*Corresponding author.



