Received December 2014

ABSTRACT

Based upon the basis of Lie super algebra B(0,1), the super Tu equation hierarchy with self-con- sistent sources was presented. Furthermore, the infinite conservation laws of above hierarchy were given.

Keywords:

Super Tu Hierarchy, Self-Consistent Sources, Conservation Laws, Lie Super Algebra

1. Introduction

Soliton equations with self-consistent sources have been receiving growing attention in recent years. Physically, the sources may result in solitary waves with a non-constant velocity and therefore lead to a variety of dynamics of physical models. For applications, these kinds of systems can be used to describe interactions between different solitary waves. Ma and Strampp systematically applied explicit symmetry constraint and binary nonlinearization of Lax pairs for generating soliton equation with sources [1]. Then, Ma presented the soliton solutions of the Schrö dinger equation with self-consistent sources [2]. The discrete case of using variational derivatives in generating sources was discussed in [3].

With the development of soliton theory, super integrable systems associated with fermi variables have been receiving growing attention. Various methods have been developed to search for new super integrable systems, Lax pairs, soliton solutions, symmetries and conservation laws, etc. [4]-[11]. In 1997, Hu proposed the super- trace identity and applied it to establish the super Hamiltonian structures of super-integrable systems [4]. Then Professor Ma gave a systematic proof of super trace identity and presented the super Hamiltonian structures of super AKNS hierarchy and super Dirac hierarchy for application [5]. The super Tu hierarchy and its super-Ha- miltonian structure was considered [6]. Recently, Yu et al. considered the binary nonlinearization of the super AKNS hierarchy under an implicit symmetry constraint [7] and the Bargmann symmetry constraint and binary nonlinearization of the super Dirac systems [8]. Meanwhile, various systematic methods have been developed to obtain exact solutions of the super integrable such as the inverse transformations, the Bä cklund and Darboux transformations, the bilinear transformation of Hirota and others [9]-[11].

This paper is organized as follows. In Section 2, the method for establishing super integrable soliton hierarchy with self-consistent sources by using Lie super algebra 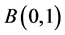was presented. For application, the super Tu hierarchy with self-consistent sources was obtained in Section 3. In Section 4, conservation laws of super Tu hierarchy were given.

2. A Kind of Super Integrable Soliton with Hierarchy Self-Consistent Sources

In the following. Consider a basis of Lie super algebra 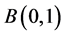[5]

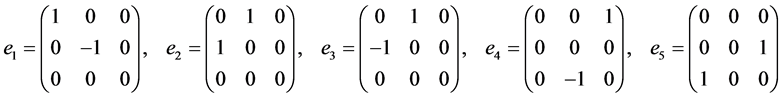. (1)

We introduce the loop algebra 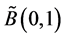as follows

(2)

where the loop algebra 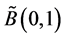is defined by .

Consider the auxiliary linear problem

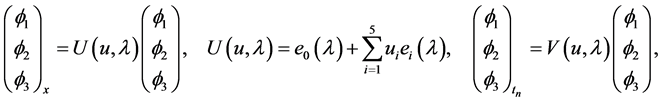(3)

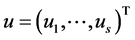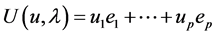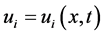
where , , , 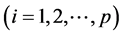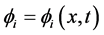are field va-

riables defining on, ,.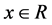

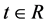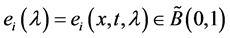From the spectral problem (3), the compatibility condition gives rise to the well-known zero curvature equation

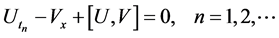(4)

The general scheme of searching for the consistent and generating a hierarchy of nonlinear equations was proposed as follows [5]. We solve the equation

, (5)

And search for, such that can be constructed by

(6)

where are linear functions of .

We consider the super trace identity of super integrable systems [4] [5]

(7)

where Str means the super trace. Defining a scalar by the equation

(8)

The sets proves the conserved densities of (4). The Hmailtonian form with can be written as

(9)

where is a recursion operator and is a symplectic operator, and .

According to (3) and (5), we consider the auxiliary linear problem. For distinct, the following systems result from (1)

(10)

Based on the results [11], we show that the following equations

(11)

where are constants. Equation (11) determines a finite dimensional invariant set for the flows (9).

For (10), it is known that

(12)

where Str denotes the super trace of a matrix and

(13)

According to (11), for a specific , we demand that

(14)

From (9) and (11), a kind of super integrable hierarchy with self-consistent sources can be present as follows

(15)

3. The Super Tu Hierarchy with Self-Consistent Sources

The super Tu spectral problem associated with Lie super algebra is given by [6]

(16)

where is a spectral parameter, and are even variables, and are odd variables [6].

Taking

The co-adjoint equation associated with (16) gives

(17)

If we set

(18)

Then (17) is equivalent to

(19)

Which results in the recurrence relations

(20)

where

(21)

Upon choosing the initial conditions

All other can be worked out by the recurrence relations (20). The first few sets are as follows:

Let us associate the problem (16) with the following auxiliary problem

(22)

The compatible conditions of the spectral problem (16) and the auxiliary problem (22) are

(23)

Which refer the super Tu equation hierarchy

. (24)

Here in (24) is called the n-th Tu flow of this hierarchy.

Using the super trace identity (7), we have

(25)

Therefore, the super Tu soliton hierarchy Equation (24) can be written as the following super Hamiltonian form:

(26)

where

Is a super symplectic operator, and is given by (25).

The first non-trivial nonlinear of super Tu hierarchy is given by its second flow

(27)

Which possesses a Lax pair of defined in (16) and defined by

Next we will establish the super Tu hierarchy with self-consistent sources. Consider the linear system

(28)

For the system (28), we consider the in the Lie super algebra and obtain

(29)

where.

According to the results in (15), the super Tu hierarchy with self-consistent sources is presented as

(30)

The first nontrivial integrable super Tu hierarchy with self-consistent sources is its second flow

(31)

When, it is the well known nonlinear Tu equation with self-consistent sources. So system (30) is a novel super integrable equation hierarchy.

4. Conservation Laws for the Super Tu Hierarchy

In what follows, we will construct conservation laws of the super coupled Burgers equation. Introduce the variables:

, (32)

where. From (10), we have

(33)

We expand in powers of as follows

, (34)

where,. Substituting (34) into (33) and comparing the coefficients of the same powers of, we obtain

(35)

And a recursion formula for and,

(36)

Because of

(37)

we derive the conservation laws of (27)

(38)

where

Assume that, , then (38) can be written as, which is the right form of conservation laws. We expand and as series in powers of according with the coefficients, which are called conserved densities and currents respectively

, (39)

where are constants of integration. Then the first two conserved densities and currents are

The recursion relations for and are

(40)

where and can be calculated from (36). The infinitely conservations laws of (36) can be easily obtained in (32)-(40) respectively.

Acknowledgements

This work was supported by the Natural Science Foundation of Henan Province (No. 132300410202), the Sci- ence and Technology Key Research Foundation of the Education Department of Henan Province (No. 12A- 110017, 14A110010), the Youth Backbone Teacher Foundation of Shangqiu Normal University (No. 2013- GGJS02).

Cite this paper

Sixing Tao, (2015) Self-Consistent Sources and Conservation Laws for Super Tu Equation Hierarchy. Journal of Applied Mathematics and Physics,03,428-435. doi: 10.4236/jamp.2015.34054

References