Journal of Applied Mathematics and Physics
Vol.03 No.04(2015), Article ID:55819,6 pages
10.4236/jamp.2015.34052
The Existence and Multiplicity of Solutions for Singular Boundary Value Systems with p-Laplacian
Zengxia Cai
School of Science, Linyi University, Linyi, China
Email: caizengxia64@163.com


Received January 2015

ABSTRACT
This paper presents sufficient conditions for the existence of positive solutions for the fourth-order boundary value problem system with p-Laplacian operator. The existence of single or multiple positive solutions for the system is showed through the fixed point index theory in cones under some assumptions.
Keywords:
Coupled Singular Boundary Value Problem, Positive Solution, Fixed Point Index Theorem

1. Introduction
In this paper, we are concerned with the existence and multiplicity of positive solutions for the system (BVP):

where ,
,  ,
,  and
and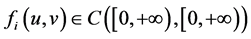 ,
, 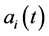 is allow- ed to have singularity at
is allow- ed to have singularity at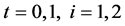 .
.
Several papers ([1]-[4]) have studied the solution of fourth-order boundary value problems. But results about fourth-order differential eguations with p-Laplacian have rarely seen. Recently, several papers ([6]-[8]) have been devoted to the study of the coupled boundary value problem.
Motivated by the results mentioned above, here we establish some sufficient conditions for the existence of to (BVP) (1.1) under certain suitable weak conditions. The main results in this paper improve and generalize the results by others.
The following fixed-point index theorem in cones is fundamental.
Theorem A [9] Assume that 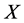 is a Banach space,
is a Banach space, 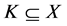 is a cone in
is a cone in , and
, and ,
,
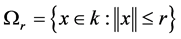 , if
, if  is a completely operator and
is a completely operator and ,
, .
.
1) If for ,
, 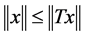 , then i
, then i
2) If for


2. Preliminaries and Lemmas
In this paper, let 


ce with the norm







Suppose 


Obviously, 

Define a cone 

define an integral operator 

Let us list the following assumptions for convenience.


Lemma 2.1 

It is easy to see that 

Lemma 2.2 Suppose that 

Lemma 2.3 Suppose that 

Proof Firstly, assume 
Then 

Secondly, suppose



Due to the continuity of

Theorem, then 


Lastly, since 




Then for all
So 

Therefore, 
For convenience we denote
3. Main Results
Theorem 3.1 Suppose that 


Then the system (1.1) has at least one positive solution
Proof By Lemma 2.3, we know 









Hence,


erefore


On the other hand, from












Hence,

If







Therefore it follows from the fixed-point theorem that 



Theorem 3.2 Suppose that 



Then the system (1.1) has at least one positive solution
Proof By lemma 2.3, we know 








Let



Hence,
If






always may set


On the other hand, from





Case (i). Suppose that 





we get
Hence,


then

Case (ii). Suppose that 







2. Let

Hence,


so




Therefore it follows from the fixed-point theorem that 



Remark 3.1 Note that if 

Remak 3.2 When 

Theorem 3.3 Suppose that 









Proof. Choosing 











Hence,





On the other hand, From (H6), if









Hence,


If





we always may set


Therefore it follows from the fixed-point theorem that 



Theorem 3.4 Suppose that 









The proofs are similar to that of Theorem 3.2 and are omitted.
Theorem 3.5 Assume that 



Then the system (1.1) has at least two positive solutions 


Theorem 3.6 Assume that 



Remark 3.3 Under suitable weak conditions, the multiplicity results for fourth-order singular boundary value problem with 
Cite this paper
Zengxia Cai, (2015) The Existence and Multiplicity of Solutions for Singular Boundary Value Systems with p-Laplacian. Journal of Applied Mathematics and Physics,03,411-416. doi: 10.4236/jamp.2015.34052
References
- 1. Korman, P. (2004) Uniqueness and Exact Multiplicity of Solutions for a Class of Fourth-Order Semilinear Problems. Proceedings of the Royal Society of Edinburgh Section A—Mathematics, A134, 179-190. http://dx.doi.org/10.1017/S0308210500003140
- 2. Ma, R. and Wu, H. (2002) Positive Solutions of a Fourth-Order Two-Point Boundary Value Problem. Acta Mathematica Sinica, A22, 244-249. (In Chinese)
- 3. Yao, Q. (2004) Positive Solutions for Eigenvalue Problems of Fourth-Order Elastic Beam Equations. Applied Mathematics Letters, 17, 237-243. http://dx.doi.org/10.1016/S0893-9659(04)90037-7
- 4. Ma, R.Y. and Wang, H.Y. (1995) On the Existence of Positive Solutions of Fourth-Order Ordinary Differential Equations. Applicable Analysis, 59, 225-231. http://dx.doi.org/10.1080/00036819508840401
- 5. Sun, W.P. and Ge, W.G. The Existence of Positive Solutions for a Class of Nonlinear Boundary Value Problems. Acta Mathematica Sinica, 44, 577-580. (In Chinese)
- 6. Agarwal, R.P., O’Regan, D. and Wong, P.J. (2000) Positive Solutions of Differential. Difference and Integral Equations. Springer-Verlag, Singapore.
- 7. Ma, R.Y. (2000) Multiple Nonnegative Solutions of Second-Order Systems of Boundary Value Problems. Nonlinear Analysis, 42, 1003-1010. http://dx.doi.org/10.1016/S0362-546X(99)00152-2
- 8. Ni, X.H. and Ge, W.G. (2005) Existence of Positive Solutions for One-Dimensional p-Laplacian Coupled Boundary Value Problem. J. Math. Rese. Expo., 25, 489-494. (In Chinese)
- 9. Guo, D.J. (2000) Nonlinear Functional Analysis. Science and Technology, Jinan.




























