Journal of Applied Mathematics and Physics
Vol.03 No.04(2015), Article ID:55793,6 pages
10.4236/jamp.2015.34050
Mathematical Model of Anisotropy of Magnetic Susceptibility (AMS)
William W. Guo
School of Engineering & Technology, Central Queensland University, North Rockhampton, Australia
Email: w.guo@cqu.edu.au


Received January 2015

ABSTRACT
Magnetic susceptibility of natural rocks and ores is important in many applications. In a few rock types magnetic susceptibility is independent of the direction in which a weak magnetic field is applied. Such rocks are magnetically isotropic. In most rock types, however, the magnitude of magnetic susceptibility in a constant weak field depends on the orientation of the magnetic field applied. Such rocks are magnetically anisotropic and such directional variation in magnetic susceptibility with these rocks is termed as anisotropy of magnetic susceptibility (AMS). Although attempts have been made on describing AMS using mathematical models, there is still a need to present a more consistent and united mathematical process for AMS. This paper presents a united AMS model by rationalizing the existing pieces of different AMS models through a consistent approach. A few examples of AMS from some types of natural rocks and ores are also presented to substantiate this united AMS model.
Keywords:
Magnetic Susceptibility, Anisotropy of Magnetic Susceptibility (AMS), Mathematical Model, Susceptibility Ellipsoid

1. Introduction
Magnetic susceptibility of natural rocks and ores plays important roles either directly or indirectly in many applications, such as oil and mineral explorations [1]-[3], geology [4], climate change and environment assessment [5] [6], mining and metallurgy [7] [8], and archeology [9]. However, magnetic susceptibility of many types of rocks and ores is not isotropic, i.e., the magnitude of magnetic susceptibility of some rocks and ores varies with the orientation of the rocks and ores with respect to the measurement of magnetic susceptibility. Such directional variation in magnetic susceptibility with some rocks and ores is termed as anisotropy of magnetic susceptibility (AMS).
AMS is a reflection of uneven and directed distribution of ferromagnetic minerals in some rocks and ores during their formation or later deformation by various means. Effect of AMS can be either positive, such as identifying historic structural and tectonic events through magnetic fabrics in the rocks [10]-[12], or negative, such as complicating magnetic modelling of iron-ores hosted in banded iron formations [13] [14].
Some attempts have been made on describing AMS using mathematical models [13]-[17]. However, there is still a need to present a more consistent and united process to describe the mathematical model for AMS. This paper fills the gap by rationalizing the existing pieces of different AMS models through a consistent approach that leads to a united presentation of AMS model. A few examples of AMS from some types of natural rocks and ores are also presented to substantiate this united AMS model.
2. Conceptions of Magnetic Susceptibility and Anisotropy of Magnetic Susceptibility (AMS)
Magnetic susceptibility 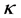 is defined by
is defined by
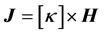 (1)
(1)
where  is the induced magnetization of the material and
is the induced magnetization of the material and 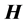 is the applied magnetic field. As both
is the applied magnetic field. As both  and
and , in the Systeme International (SI), are expressed in amperes per meter, volumetric susceptibility
, in the Systeme International (SI), are expressed in amperes per meter, volumetric susceptibility  is dimensionless, and mass susceptibility is expressed in cubic meters per kilogram. Susceptibility varies as a function of temperature and the strength and frequency of the applied field. In most cases, susceptibility is assumed to be that measured at room temperature (~20˚) and the assumption that
is dimensionless, and mass susceptibility is expressed in cubic meters per kilogram. Susceptibility varies as a function of temperature and the strength and frequency of the applied field. In most cases, susceptibility is assumed to be that measured at room temperature (~20˚) and the assumption that  versus
versus 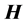 is linear is generally acceptable in direct current fields of less than 1 mT. In such conditions, experimental procedures are the easiest, allowing rapid measurements, and
is linear is generally acceptable in direct current fields of less than 1 mT. In such conditions, experimental procedures are the easiest, allowing rapid measurements, and  is a good estimate of the induced magnetization due to the Earth’s magnetic field.
is a good estimate of the induced magnetization due to the Earth’s magnetic field.
It is important to distinguish extrinsic or measured susceptibility , which is the susceptibility conven- tionally measured by most instruments, from intrinsic susceptibility
, which is the susceptibility conven- tionally measured by most instruments, from intrinsic susceptibility , which is the true susceptibility after removal of the effects of internal demagnetization fields [13] [14]. The two susceptibilities have a simple rela- tionship:
, which is the true susceptibility after removal of the effects of internal demagnetization fields [13] [14]. The two susceptibilities have a simple rela- tionship:
 , (2)
, (2)
where N is the demagnetization factor. When  SI, demagnetization effects are insignificant; thus
SI, demagnetization effects are insignificant; thus .
.
In a few rock types the induced magnetization in symmetrically shaped specimens is independent of the direction in which a weak magnetic field is applied. Such rocks are magnetically isotropic. In most rock types, however, the strength of the induced magnetization in a constant weak field depends on the orientation of a rock sample within the field. Such rocks are magnetically anisotropic. The variation of susceptibility with orientation can be described mathematically in terms of a symmetric second-rank tensor as,
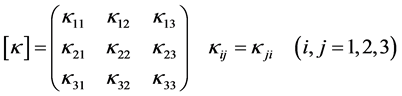 , (3)
, (3)
Or simply visualized as a susceptibility ellipsoid (Figure 1). This characteristic of rocks is termed the aniso-
Figure 1. Anisotropy of magnetic susceptibility (AMS) ellipsoid.
tropy of magnetic susceptibility (AMS). A more detailed mathematical description of AMS follows in the next section.
3. Mathematical Description of Anisotropy of Magnetic Susceptibility (AMS)
Susceptibility is a second-rank tensor expressed as Equation (3). Because it is symmetric, it can be converted to another specialized orthogonal coordinate system by rotating the coordinates,

where



By Equations (1) and (4), in the new coordinates, the populations of induced magnetization are expressed as

or

This indicates that the three principal susceptibilities are parallel to their corresponding populations of magnetic field, and no interactions occur among the three orthogonal populations.
We do not normally measure each component of the susceptibility tensor. Instead, we measure the directional susceptibility along the applied magnetic field. For an anisotropic material, assuming there is an angle 






If the direction cosines of 


Then the directional susceptibility 

As



In practice, the susceptibility tensor of a sample can be calculated by means of the least-squares method from a set of 
Assuming there is a vector 



Then the direction cosines are

From Equations (10)-(12), the following equation can be determined

This is a ternary quadratic polynomial that can be converted to an ellipsoid using the three eigenvectors coincident with the three principal susceptibilities:

This is called the magnitude susceptibility ellipsoid or simply the susceptibility ellipsoid. It is a standard ellipsoid with the half-axis length of
The output of AMS measurements is the susceptibility ellipsoid defined by the length and orientation of its three principal axes. The parameters usually presented are the bulk susceptibility

And the magnetic anisotropy A, lineation L and foliation F as given below

The magnetic foliation plane contains the maximum and intermediate susceptibility axes. The magnetic lineation is parallel to the maximum susceptibility axis, so it lies within the foliation plane. The minimum susceptibility axis is normal to the magnetic foliation plane so it can be regarded as the pole to the foliation plane (Figure 1).
4. Examples of AMS of Rocks and Iron Ores
The magnitude of AMS depends on two factors: the anisotropy of individual magnetic particles; and the degree of their alignment. The anisotropy of the individual particles comprises two populations-crystalline and shape anisotropy. The preferred orientation of crystallographic axes commonly controls grain shape and determines the AMS for the vast majority of minerals. However, for a few special rock types, such as banded iron formations (BIFs), ferromagnetic grains are concentrated along some bands. In such cases the magnetic interactions among the ferromagnetic grains can generate an overall magnetic behavior completely different from the behavior of individual grains. This type of anisotropy is often called textural anisotropy [18]-[20]. BIFs have a well-developed magnetic foliation parallel or sub-parallel to bedding, which are shown in Figure 2. In both cases, the pole to the bedding almost coincides to the minimum axis of magnetic susceptibility ellipsoid. The degree of anisotropy of these BIFs is greater than 1.2, meaning the magnitude of the maximum susceptibility is 20% stronger than that of the minimum susceptibility.
High-grade iron ores derived from BIFs have a weak AMS and the average degree of anisotropy is below 1.05 (Figure 3). Compared with AMS of BIFs, these iron ores are generally isotropic in susceptibility although a recognizable sub-bedding-parallel magnetic foliation can be seen.
Basalt and dolomite are weak in magnetism and generally isotropic (Figure 4).
Figure 2. Anisotropy of magnetic susceptibility (AMS) of BIFs from Hamersley Province of Western Australia.
Figure 3. Anisotropy of magnetic susceptibility (AMS) of high-grade hematite ores hosted in BIFs in Hamersley Province.
Figure 4. Isotropy of magnetic susceptibility of basalt and dolomite in Hamersley Province.
5. Conclusion
This paper presents a united AMS model by rationalizing the existing pieces of different AMS models through a consistent approach. A few examples of AMS from some types of natural rocks and ores are also presented to substantiate this united AMS model. This unified mathematical model serves as a consistent guide for any studies involving AMS.
Cite this paper
William W. Guo, (2015) Mathematical Model of Anisotropy of Magnetic Susceptibility (AMS). Journal of Applied Mathematics and Physics,03,399-404. doi: 10.4236/jamp.2015.34050
References
- 1. Aifa, T., Zerrouki, A.A., Baddari, K. and Géraud, Y. (2014) Magnetic Susceptibility and Its Relation with Fractures and Petrophysical Parameters in the Tight Sand Oil Reservoir of Hamra Quartzites, Southwest of the Hassi Messaoud Oil Field, Algeria. Journal of Petroleum Science and Engineering, 123, 120-137. http://dx.doi.org/10.1016/j.petrol.2014.05.029
- 2. Guo, W., Dentith, M.C., Bird, R.T. and Clark, D.A. (2001) Systematic Error Analysis of Demagnetization and Implications for Magnetic Interpretation. Geophysics, 66, 562-570. http://dx.doi.org/10.1190/1.1444947
- 3. Guo, W.W., Li, Z.X. and Dentith, M.C. (2011) Magnetic Petrophysical Results from the Hamersley Basin and Their Implications for Interpretation of Magnetic Surveys. Australian Journal of Earth Sciences, 58, 317-333. http://dx.doi.org/10.1080/08120099.2011.552984
- 4. Balla Ondoa, A., Ngos III, S., Ndjeng, E., Abolo, A. and N’Nanga, A. (2014) Contribution of the Magnetic Susceptibility to the Characterization of the Babouri-Figuil Cretaceous Basin. Open Journal of Soil Science, 4, 272-283. http://dx.doi.org/10.4236/ojss.2014.48029
- 5. Balsam, W., Ji, J.F. and Chen, J. (2004) Climatic Interpretation of the Luochuan and Lingtai Loess Sections, China, Based on Changing Iron Oxide Mineralogy and Magnetic Susceptibility. Earth and Planetary Science Letters, 223, 335- 348. http://dx.doi.org/10.1016/j.epsl.2004.04.023
- 6. Gautam, P., Blaha, U. and Appel, E. (2005) Magnetic Susceptibility of Dust-Loaded Leaves as a Proxy of Traffic-Related Heavy Metal Pollution in Kathmandu City, Nepal. Atmospheric Environment, 39, 2201-2211. http://dx.doi.org/10.1016/j.atmosenv.2005.01.006
- 7. Guo, W.W. (2010) A Novel Application of Neural Networks for Instant Iron-Ore Grade Estimation. Expert Systems with Applications, 37, 8729-8735. http://dx.doi.org/10.1016/j.eswa.2010.06.043
- 8. Chen, C.W. (1977) Magnetism and Metallurgy of Soft Magnetic Materials. North-Holland, Amsterdam.
- 9. Dalan, R.A. (2008) A Review of the Role of Magnetic Susceptibility in Archaeogeophysical Studies in the USA: Recent Developments and Prospects. Archaeological Prospection, 15, 1-31. http://dx.doi.org/10.1002/arp.323
- 10. MacDonald, W.D. and Ellwood, B.B. (1987) Anisotropy of Magnetic Susceptibility: Sedimentological, Igneous, and Structural-Tectonic Applications. Reviews of Geophysics, 25, 905-909. http://dx.doi.org/10.1029/RG025i005p00905
- 11. Borradaile, G.J. (1988) Magnetic Susceptibility, Petrofabrics and Strain. Tectonophysics, 156, 1-20. http://dx.doi.org/10.1016/0040-1951(88)90279-X
- 12. Borradaile, G.J. and Henry, B. (1997) Tectonic Application of Magnetic Susceptibility and Its Anisotropy. Earth-Science Reviews, 42, 49-93. http://dx.doi.org/10.1016/S0012-8252(96)00044-X
- 13. Clark, D.A. and Schmidt, P. (1986) Magnetic Properties of the Banded-Iron Formations of the Hamersley Group, WA. CSIRO Division of Mineral Physics, AMIRA Report 1638.
- 14. Guo, W. (1999) Magnetic Petrophysics and Density Investigations of the Hamersley Province, Western Australia: Implications for Magnetic and Gravity Interpretation. The University of Western Australia, Perth.
- 15. Runcorn, S.K. (1967) The Anisotropy of Magnetisation of Rocks. In: Collinson, D.W., Creer, K.M. and Runcorn, S.K., Eds., Methods in Palaeomagnetism, Elsevier, Amsterdam, 353-359.
- 16. Tarling, D.H. and Hrouda, F. (1993) The Magnetic Anisotropy of Rocks. Chapman & Hall, London.
- 17. Dunlop, D.J. and Ozdemir, O. (1997) Rock Magnetism. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511612794
- 18. Porath, H. and Chamalaun, F.H. (1968) Palaeomagnetism of Aus-tralian Haematite Ore Bodies, II, Western Australia. Geophys. Geophysical Journal International, 15, 253-264. http://dx.doi.org/10.1111/j.1365-246X.1968.tb00184.x
- 19. Schmidt, P. and Clark, D.A. (1994) Palaeomagnetism and Magnetic Anisotropy of Proterozoic Banded-Iron Formations and Iron Ores of the Hamersley Basin, Western Australia. Precambian Research, 69, 133-155.
- 20. Guo, W.W. Modelling Textural Anisotropy of Magnetic Susceptibility of Banded Iron Formations. Journal of Applied Mathematics and Physics. (In Press)





