 Journal of Power and Energy Engineering, 2015, 3, 313-318 Published Online April 2015 in SciRes. http://www.scirp.org/journal/jpee http://dx.doi.org/10.4236/jpee.2015.34042 How to cite this paper: Chen, G., Lu, E., Peng, C.Y., Hou, Y.H., Qin, Z.J., Huang, S.W. and Liu, F. (2015) Coordinating Preven- tive Strategies and Restoration under Extreme Weather Conditions. Journal of Power and Energy Engineering, 3, 313-318. http://dx.doi.org/10.4236/jpee.2015.34042 Coordinating Preventive Strategies and Restoration under Extreme Weather Conditions Gang Chen1, En Lu1, Chaoyi Peng2, Yunhe Hou2, Zhijun Qin2, Shaowei Huang3, Feng Liu3 1Guangdong Power Grid Dispatching Center, Guangdong Power Grid Co. Ltd., Guangzhou, China 2Department of Electrical and Electronic Engineering, The University of Hong Kong, Hong Kong, China 3Department of Electrical Engineering, Tsinghua University, Beijing, China Email: hbluen@163.com, pcy1990@eee.hku .hk, yhhou@eee.hku.hk, zjqin@eee.hku.hk, huangsw@mail.singhua.edu.cn, lfeng@mail.tsinghua.edu.cn Received February 2015 Abstract It has been well identified that the extreme events significantly impact the system operation. In this work, a comprehensive operating strategy, which coordinates the preventive strategies and system restoration, was proposed. A re-dispatch model that limits the potential loss under ex- treme events, as well as provides adequate resources for system restoration after the extreme events, was proposed. An optimal power flow based method was established to solve the proposed model. The availabilities of components and the remaining system due to the extreme events were restored by extending the EPRI’s System Restoration Navigator (SRN) with a little modification. Case studies demonstrate the proposed model and methods. Keywords Extreme Weather Event, Preventive Strategy, Restoration, Coordination 1. Introduction A power system is designed to balance the demand effectively and reliably under various operating conditions. New challenges associated with climate change have been identified, not only in short-term planning but also in the long-term planning [1]. It was predicated by the World Business Council on Sustainable Development (WBCSD), due to wind damage, sea level rise, and storm surges, over the next 20 years, in Gulf of Mexico area, the cumulative losses will exceed US$ 350 billion, which is 2% - 3% of the region’s GDP [2]. The losses due to the short-term extreme events have been well witnessed every year. For instance, US$ 65 billion was spent to re- pair the damage caused by the supper cyclone Sandy in New York in 2012. In Asia, CLP Power Hong Kong re- ported that between 2005 and 2008, typhoons caused power outages on four occasions. Typhoon Jangmi in 2008 resulted in 17 days power cuts [3]. According to Electric Power Research Institute (EPRI), China, extreme weather conditions are the second most influential factor challenging power systems’ stability. In 2014 Power and Energy Society General Meeting, these issues are specifically discussed in sessions such as “Extreme Events and Disas-  G. Chen et al. ter Management-Global Perspective” and “Power System Planning and System Reliability”. As a result, the power sector has to consider the strategies to meet the changes due to the global warming. In the long-term planning, an early climate-related risk assessment should be involved; meanwhile, in the short-term operation, strategies for different weather patterns, especially for more frequent extreme weather events, have to be considered [3]. To meet the increasing climate change related requirements, the self-healing or resilience characteristic has been well identified as one of the critical functionalities of the future energy infrastructure [4]. In WBCSD’s re- port entitled “Building a Resilient Power Sector” released in 2014, WBCSD’s Action 2020 climate change business solution was proposed [2]. Action 2020 will develop 12 business solutions; building resilience in the power sector is one of them. The “resilience” includes a timely and efficient preservation and restoration under all operating scenarios. To operate power systems under extreme weather condition, some industrial and academic research work has been triggered. For instance, the IEEE Standard 346 divided weather conditions into three categories, i.e., nor- mal, adverse, and major storm disaster. A multi-state weather models for the transmission and distribution sys- tem were established based on IEEE Standard 346 [5]. More sophisticated stochastic models according to his- torical data were discussed and used for risk analysis [6]. In this work, stochastic availability models will be used. The operation strategy can be established based on the risk associated with the extreme events. The work concerns the operating strategies under the extreme weather conditions. Preventive strategies and restoration will be included. In this area, although the critical requirements were well identified, the major work still focuses on the functionality identification and document best practices of industry. Until now, major work based on the assumption that all required information is given. In [7], the stochastic availability model was in- troduced into the system restoration. This method proposed in this paper will link the preventive strategies with the system restoration. The preventive strategy mitigates vulnerability, as well as provides adequate resources for system restoration after the extreme weather events. The restoration method will extend the work described in [7], and be integrated into the EPRI’s System Restoration Navigator (SRN) with stochastic availability model. 2. Availability Models of Components under Extreme Events Based on historic data of US [6] [8] and China, in this paper, the extreme weather conditions concern the icing, typhoon, and earthquake. 2.1. Outage Probability under Covering Ice As for the impact of covering ice on transmission lines, the main factor of outage probability is the thickness of covering ice. Denote Das the designed rated capacity of covering ice thickness, and b is the thickness of covering ice. This work respectively designates that the outage probability is zero and one, when b does not exceed D and b exceeds 5D, while exponentially increases between D and 5D: ()( ) 0, ; 0.6931 exp1,5 ; 4 1,5 . F bD bD bDb D D bD λ ≤ − =− << ≥ (1) 2.2. Outage Probability under Typhoon Transmission lines have a designed rated capacity of wind speed withstanding, which is denoted V here. Denote the wind speed as v. The work designates that the outage probability is zero and one, when v does not exceed V, and when v exceeds 2V, while increases exponentially between V and 2V: ( )( ) 0, ; 0.6931 exp1,2 ; 2 1,2 . F vV vV vVv V V vV λ ≤ − =− << ≥ (2)  G. Chen et al. 2.3. Outage Probability under Earthquake Earthquake possibly breaks tower foundation leads to the outage of transmission lines. An anti-seismic capacity is designated when transmission lines are constructed. Denote it as W, which is a rated seismic intensity level. Assume a level w earthquake happens. Respectively designate that the outage probability is zero and one, when w does not exceed W and when w exceeds W + 1, while increases between W and W + 1: ( ) 0, ; , 1; 1, 1. F wW wwWW wW wW λ ≤ =−<< + ≥+ (3) Since when any of the above-defined indices reaches the limit, transmission line outage happens, an inte- grated index of outage probability should be defined: () () () { } max, , F FFF bvw λ λλλ = (4) 3. Preventive Strategies under Extreme Weather Conditions The objective of the preventive strategies is to mitigate the potential influence of an extreme weather event, in which following activities are conducted: 1) Closing the parallel transmission lines to strengthen the network. 2) Identifying the critical components and paths, and their outage probability is computed from Section 2. 3) Re-dispatching the system to reduce the power flow and load on the transmission lines in the center of the predicated extreme weather event. These activities are presented in detail in this section. 4) Preparing backup resources. With the method proposed in [7], the restoration based on the availability con- straint can be established. 3.1. Preventive Strategy Under the condition that the availabilities of each component are quantified by the models proposed in Section 2, an optimal power flow based re-dispatch scheme is described as follows. 1) Objective function ( ) ( ) 1 01 min sum LL f = ×− Xc. PP (5) where , are the load vectors before and after re-dispatch, respectively, is the cost coefficient vectors for load shedding, × is element-wise multiplication between vectors or between matrices. Suppose that before re-dispatch, the power flow is given and is known. 2) Constraints Equality constraints include AC power flow equations after re-dispatch. ( ) () () () () 11 1111111111 111 11111 1111 GL CL h −−×−−×+ = = − −×−+×+ PPe.GeBff .GfBe x0 QQf.GeBfe. GfBe (6) where and are vectors of active and reactive power loads of all buses, G1 and B1 are real and imagi- nary part of admittance matrix, e1 and f1 are real and imaginary part of the voltage vector of all buses, and is reactive power output of controllable compensators, respectively. Inequality constraints include bus voltage level, active power limits of generators, VAR limits of generators and shunts. 1 11 1 11 11 1 1 11 1 11 11 () . G GG L L L CC C TT T g ≤= ≤ ×+ × × × P PP P P P Q X QQ P PP e.e f.f V. VV. V (7)  G. Chen et al. where , : lower and upper limits of variables, is the real power vector on each transmission line. By shedding load, the generators’ outputs and power flow on transmission lines in the area with potential in- fluence of the extreme event will be limited. 3.2. Coordinating Preventive Strategy with Restoration The method described in part 3.1 has been widely used in industry. Usually, this method can reduce the potential loss by reducing the load level and the power flow. However, for the area with high percentage coal units, the remaining system after the extreme events might be difficult for restoration. The preventive strategy should maintain adequate on-line generating units, especially the large non-blackstart units, after the extreme event happens, because the restoration of large non-blackstart units is very time con- suming. Physically, after losing some components due to the extreme event, some generating units have to be shut down, due to the minimal outputs constraint, to balance the reduced load level. Mathematically, the re-dis- patch model (5)-(7) cannot find a solution. To avoid this problem, the system state after re-dispatch and after the extreme events should be involved in one OPF model as follows. 1) Objective function ( ) () () 101 212 min sum LL LL f =×−+× − Xc.P Pc.PP (8) where , and c1 are the same as (5), load vectors is the load level after loss some components with low availabilities due to the extreme events, c2 is cost coefficient vectors for loss of load due to the extreme events. 2) Constraints Equality constraints include AC power flow equations after re-dispatch and after loss some components with low availabilities due to the extreme events. After re-dispatch, the power flow equation is the same as (6). After the extreme events, let G2 and B2 are real and imaginary part of the admittance matrix after losing some components with low availabilities. The power flow equation will be ( ) ()() ()() 222 22222 2222 222 22222 2222 .. .. GL CL h −−×− −×+ = = − −×−+×+ PPeGe BffGfBe x0 QQ fGe BfeGfBe (9) where , are vectors of active and reactive power loads of all buses,e2 and f2 are real and imaginary part of the voltage vector of all buses, and is reactive power output of controllable compensators, respectively. Inequality constraints includes bus voltage level, active power limits of generators, VAR limits of generators, and shunts after re-dispatch and after the extreme event. ( ) .. ... k kkG GGk kkL LL k k kCC Ckk kTT Tkkkk kk kk g ≤= ≤ ×+× × × P PP P P P XQ QQ P PP eef f VV VV (10) where the notations are the same as (7). By solving the model described by (6), (8), (9), and (1 0) , the generating units will be survived after the ex- treme events. System restoration can be implemented based on all available generation resources. 4. Illustrative Example The proposed methods are demonstrated in this section. A built-in 23-bus testing system of PSS/E is used to il- lustrate the proposed methods. Two preventive strategies proposed in Section 3 are validated in this system. The remaining system is restored with the extended EPRI’s SRN. 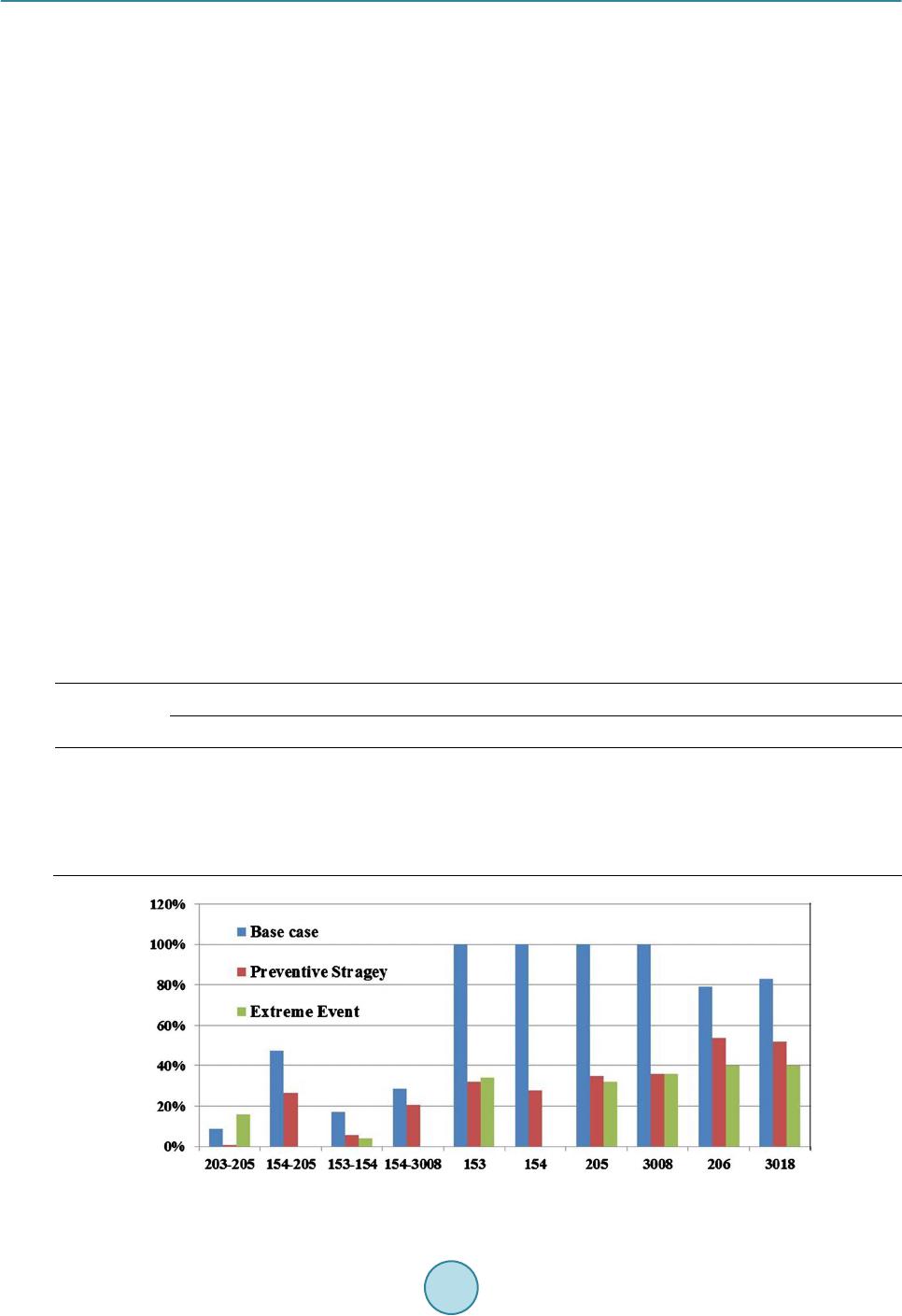 G. Chen et al. 4.1. Base Case In the base case, one line between bus 203 and 205, and one line between bus 153 and 154 are out of service. The output of the generating unit on bus 206 is 79.17 MW (79.17% rated capacity)/35.22 MVar. The output of generating unit on bus 3018 is 100.00 MW (83% rated capacity)/73.35 MVar. These two generating units are coal units with minimal outputs are 40% rated capacities. The rated capacities of generating unit on bus 206 and bus 3018 are 100 MW and 120 MW, respectively. The load levels in this critical area are listed in Table 1. 4.2. Results of the Preventive Strategy The preventive strategy described in Section 3.1 is illustrated. In the area, it is assumed that all lines are put into service and parts of loads are shed to a low level by the re-dispatch strategy. The real power outputs of generat- ing units on bus 206 and bus 3018 are 54.35 MW (54.35% rated capacity) and 62.78 MW (52% rated capacity), respectively. The load level at each bus is summarized in Table 1. In this case, the generating units’ outputs are very close to the minimal outputs, i.e., 40% of the rated capaci- ties. Under the extreme event, in the critical area, if the loads on bus 154 and the line 154-205 are lost, the gene- rating unit on bus 3018 and bus 206 has to be shut down due to the minimal output constraints. Under this condition, after the extreme event, system restoration strategy has to crank two large non-blackstart units. Restoration for generating unit on bus 3018 and bus 206, if no preventive control with coordination, it is assumed that the start requirement of the generating unit is 15% of its capacity. The other parameters can be found in [7]. After simulating by SRN, these interrupted generating units will be cranked within 20 minutes. However, it is still a time-consuming process to put these units into parallel. 4.3. Results of Coordinating Strategy By solving the he model described by (6), (8), (9), and (10), the generating units will be survived after the ex- treme events. After losing the load on bus 154 and the line 154-205, the outputs of generating units on bus 206 and 3018 are still larger than the minimal outputs, as shown in the Figure 1. Table 1. Load Levels for base case and after preventive strategy. Bus Base Case After preventive strategy P (MW) Q (MVar) P (MW) Q (MVar) 153 100 50 32 15 154 180 80 50 24 205 120 70 42 21 3008 200 175 72 52.5 Figure 1. The load level on lines, load and generating units by the coordinating strategy.  G. Chen et al. Since two generating units are still survived by the coordinating re-dispatch strategy, the restoration duration described in Section 4.1 will not be needed after the extreme event. 5. Conclusion This paper proposed a comprehensive method to coordinate the preventive strategy and restoration under the ex- treme weather events. Based on the predicted extreme events, the availability of each component is quantified first. And then, the preventive strategies are designed in the area of extreme events by reducing load levels and strengthening the network. An OPF-based re-dispatch method was proposed. To ensure the sufficient resources for the system restoration, the system state after losing some critical components due to the extreme events is also integrated into the OPF-based re-dispatch model. An interior point method is established to solve the pro- posed model. By extending the EPRI’s SRN with an availability constraint, the remaining system is restored and returns to the normal operating condition. The proposed method can limit the potential loss due to the extreme events, as well as provide adequate resources for system restoration after the extreme weather events. References [1] NERC. Special Report: Electric Industry Concerns on the Reliability Impacts of Climate Change Initiatives. www.nerc.com [2] (2014) World Business Council for Sustainable Development (WBCSD). Building a Resilient Power Sector. http://www.wbcsd.org/resilience.aspx [3] Mendiluce, M. (2014) Risky Business: Building a Resilient Power Sector. IEEE Power and Energy Magazine, 12, 34- 41. http://dx.doi.org/10.1109/MPE.2014.2331892 [4] DOE (2010) Understanding the Benefits of the Smart Grid. http://www.netl.doe.gov/smartgrid/refshelf.html#Reports [5] Billinton, R. and Acharya, J. (2005) Consideration of Multi-State Weather Models in Reliability Evaluation of Tr ans- mission and Distribution Systems. Canadian Conference on Electrical and Computer Engineering, 916-922. [6] Li, G., Zhang, P. , Luh, P.B., Li, W., Bie, Z., Serna, C., et al. (2014) Risk Analysis for Distribution Systems in the Northeast U.S. under Wind Storms. IEEE Transactions on Power Systems, 29, 889 -898. http://dx.doi.org/10.1109/TPWRS.2013.2286171 [7] Hou, Y., Qin, Z. and Yan, J. (2014) Constructing Restoration Strategies with Availability Risk Constraints. Proceed- ings of 2014 IEEE PES General Meeting, Washington DC. http://dx.doi.org/10.1109/PESGM.2014.6939420 [8] Sullivan, C.R., Petrenko, V.F., McCurdy, J.D. and Kozliouk, V. (2003) Breaking the Ice [Transmission Line Icing. IEEE Industry Applications Magazine, 9, 49-54. http://dx.doi.org/10.1109/MIA.2003.1227872
|