 Journal of Power and Energy Engineering, 2015, 3, 282-288 Published Online April 2015 in SciRes. http://www.scirp.org/journal/jpee http://dx.doi.org/10.4236/jpee.2015.34038 How to cite this paper: Choi, H.D., Rhee, S.W., Ahn, C.K. and Lim, M.T. (2015) AC Scheduling Based on Thermodynamics of Indoor for On-Campus Small Data. Journal of Power and Energy Engineering, 3, 282-288. http://dx.doi.org/10.4236/jpee.2015.34038 AC Scheduling Based on Thermodynamics of Indoor for On-Campus Small Data Hyun Duck Choi, Soon Woo Rhee, Choon Ki Ahn, Myo Taeg Lim School of Electrical Engineering, Korea University, Seoul, Republic of Korea Email: chlgusejr87@korea.ac.kr, swrhee@korea.ac.kr, hironaka@korea.ac.kr, mlim@korea.ac.kr Received January 2015 Abstract This paper proposes a new day-ahead control scheme of an air conditioning (AC) based on ther- modynamic model of indoor-temperature. The thermodynamic model of ind oor-temperature can be achieved by modified first-order thermal dynamic equation. For the practical verification of proposed model, we implemented the home energy management system (HEMS) in the laboratory and used real experiment data sets. The proposed model can be represented by a state-space model of indoor-temperature and its parameters are obtained by least square algorithm. Through the proposed thermodynamic model, indoor-temperature can be predicted closely, and a behavior pattern of AC can also be achieved. This research involves the experimental verification of the proposed approach and communication architecture between the aggregator and a system user in a laboratory environment. Keywords Home Energy Management System (HEMS), Least-Square, Convex Optimization, Demand Response (DR), Air-Conditioning (AC) 1. Introduction Through the smart grid project offering a two-way communication frame, a home energy management system (HEMS) is able to manage residential load control based on measurement for the home environment, the user’s comfort, and electricity bills [1]-[3]. The main issue concerning the design of HEMS is how to provide the intel- ligent solution for energy consumption that reflects the customer’s specific lifestyle. The suitable HEMS should have the capabilities to schedule the load demands to minimize the expenditure on electricity bills and user’s uncomfortable sense simultaneously. Accurate load forecast for residential appliance is essential for efficient consumption of the electrical energy [4] [5]. In order to maintain balance between electricity production and demand on the network, accurate fore- cast for appliance load is one of the important issues in smart grid. However, residential load forecasting is usually difficult, due to its random nature of turning on/off. Many researches for residential load forecasting have been proposed over the years and still remains an important issue. Air conditioning (AC) unit is the representative appliance which belongs to the category of thermostatically controlled appliance [6]. Thus, the analysis of thermodynamic model of indoor-temperature with AC is required  H. D. Choi et al. for efficient load control. The estimation of the indoor-temperature of the next day is essential in order to predict usage of the AC load in private homes. Through the thermal dynamic model [7]-[9] of indoor-temperature, it is possible to estimate the indoor-te m- perature based on the outdoor temperature information of the following day. Based on the user’s characteristic and estimation of indoor-temperature, the AC scheduling pattern can also be predicted. The indoor-temperature is also significant information on load shifting or reducing strategy. By providing the indoor temperature infor- mation of before and after DR response to consumers, the efficient DR reaction can be led. In this paper, we propose a new day-ahead control scheme of an AC based on a modified thermodynamic model of indoor-temperature. There are extensive literatures on the thermal dynamic models of large facilities, however there are limited results in the open literatures on models for residential homes using data of relatively small size. Thus, we implemented the HEMS with smart AC in the laboratory and used real experiment data sets for the validation of the proposed method. 2. Day-Ahead Control Scheme for AC Scheduling 2.1. Modified Thermodynamic Model of Indoor-Temperature As a standard description of thermal dynamics including a residential AC, the discrete-time dynamic equation of indoor-temperature [7] can be represented as follows: [ ][ ][ ][ ] ( ) [ ][ ] ininout inAC 1TkTkTk TkP kcwk αβ + =+−+++ (1) where is the indoor-temperature at time ; is the outdoor-temperature at time ; is power consumed by AC; and is white Gaussian noise. First, we have performed validation of the model using real data collected from our laboratory. The collected data includes indoor-temperature, outdoor- temperature, and AC power usage. However, the above model did not fit well because the effectiveness of in- ternal thermal noise is simply modeled by constant scalar c. In this paper, in order to give more detailed descrip- tion for the effectiveness of internal thermal noise, we propose a modified thermal dynamic model for indoor- temperature as following form: [][ ][ ][ ] ( ) [ ][ ] () ininout inACin 1TkTkTk TkP kTk αβ χγ +=+−++ − (2) where , , and are defined above and , , and are the model parameters to be estimated. In this equation, the effectiveness of internal thermal noise is represented by the term of . denotes the temperature of internal thermal noise and it needs to be estimated. The difference between the temperature of internal thermal noise and affects the next indoor temperature in the proposed model. Based on the dynamic model in (2), the state-space form of indoor-temperature can be repre- sented as [][ ][] [ ][] 1x kAx kBu k y kCxk += + = (3) whe r e [ ][ ][ ][ ] [ ] [] [] out in AC , , 1 1, ,1. Tk xkT kukPk A BC αχα βχγ == = −−== (4) As a model fitting method, we use a least-square (LS) algorithm. ( ) [][ ][ ] ( ) 2 ,1 ˆˆ ,arg min1 N AB k ABxkAxk Bk = =+− + ∑ (5) where N is the number of observations used in the parameter estimation. In this study, we considered the case  H. D. Choi et al. when N corresponds to 30 days of measurements. The model extracted from the data needs to be validated using real experiment data sets. With the estimated parameters , , and obtained from data set, we test the accuracy of the model using a different data set. Based on the state-space model, the prediction of indoor- temperature can be obtained [][ ][ ] ˆˆ ˆ1x kAx kBuk+= + (6) The mean squared Prediction Error (PE) is given by [][] 1 2 1ˆ11 N pk exk xk N= =+− + ∑ (7) The validation of indoor-temperature prediction is given in Section 3. 2.2. Optimization Framework for HEMS Based on the Modified Thermodynamic Model The residential consumer’s interest is two-fold. One is to minimize residential consumer payment and the other is the user’s comfort. It is clear that these two objectives can be conflicting in many scenarios. One of the im- portant issues for optimization problem in HEMS is how to select a cost index for user’s comfort. If one can predict user’s power consumption pattern for next day, cost selection problem becomes easy. Taking this into consideration, we can get the cost function to be minimized as follows: [ ][][ ][] ( ) 2 ACin in 1 ˆ Nr P k JC kPkT kT k σδ = = +− ∑ (8) where is the prediction of indoor-temperature considering the usual power usage pattern; is electricity price; is power consumed by AC; and are adjusting weight parameters. The first and second terms of the objective function in (8) denote the total electricity payment amount and the total cost of uncomfortableness, respectively. As shown in (8), user’s discomfort index becomes simply the distance from the normal pattern which can be obtained by estimation of indoor-temperature and user’s AC operating guide. Based on the cost function in (8), we can formulate the optimal AC scheduling problem as the following con- strained optimization framework: [][ ][ ] AC AC AC 11 min ˆˆ .1 0, P NN r kk J stxkAx kBu k PP λ = = += + ≤≤ ∑∑ (9) where is normal AC load based on the prediction indoor-temperature and user’s pattern; is load reduc- tion ratio. As shown in (9), the thermodynamic of indoor-temperature and can be integrated as constraint. The optimization variables are the energy consumption scheduling vectors for AC. Given the feasible AC sche- duling sets and the model in (3), the goal is to find the best AC scheduling vectors to make the cost minimize. 3. Experimental Results 3.1. Experiment Setup Environment for Measurement Data For the practical verification of proposed method, we implemented the HEMS with smart AC in the laboratory and used real experiment data sets. Figure 1 shows the HEMS setup operated by laptop and micro controller unit (MCU) in our laboratory environment. The experiment was carried out in the research laboratory in the Department of Electrical Engineering at Korea University. This 35 m2 house is designed to represent real living space for three people. In our experiment, a smart AC which is possible to communicate with MCU for DR was used. The MCU consists of SEP 2.0 communication unit, control unit for AC usage, and AC power measuring unit. The HEMS consists of a laptop with Internet connectivity that runs the HEMS program and can be com- municated with the smart AC through Korean DR protocols (Open ADR 2.0/SEP 2.0) standard. Detailed speci- fications of equipment for HEMS in laboratory are shown in Table 1. The loading profile of the smart AC is 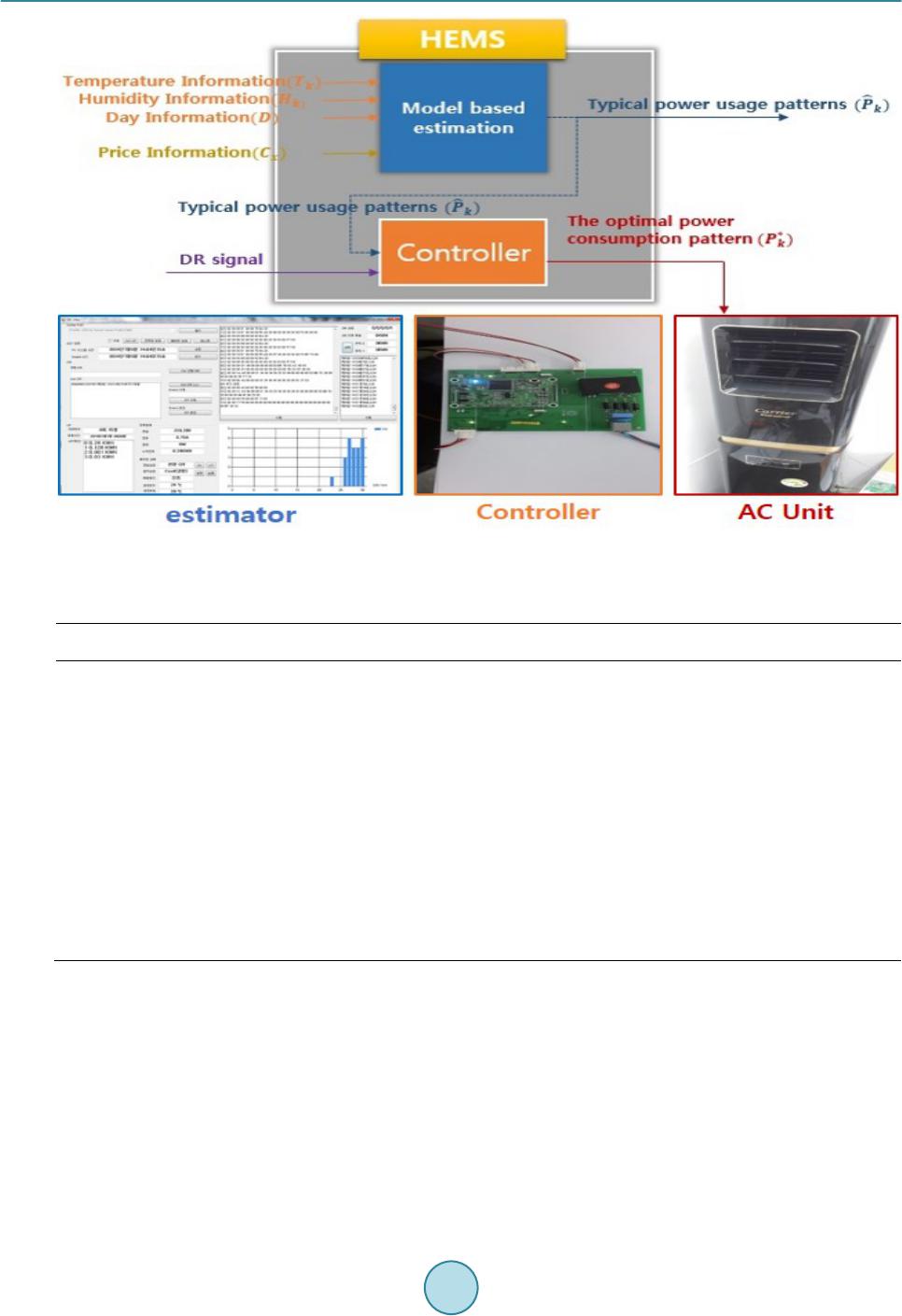 H. D. Choi et al. Figure 1 . Layout of HEMS and setup environment. Table 1. Device configuration. Laptop Model Processor Memory OS Lenovo ThinkPad E540 4 GB Windows 7 32 bit MCU Model Fun ction Communication Perform ance ATmega2560 communication with Server and AC operating AC with DR level interface: RS232C communication level: TTL Flash: 256 KB Max operating Frequency : 16MHz Smart AC Model Fun ction Voltage Current Carrier CPM-A157TGB0 Air Conditioner Dehumidi fier 220 V 8.1 A obtained by MCU measurement data, which has been measured for 30 days in the area where the house is lo- cated. In the same manner, MCU has ability to turn on/off AC using its own outputs. Indoor-temperature and humidity were obtained through the thermostat and outdoor-temperature brought in meteorology. Using these collected data, we validate the effectiveness of the proposed prediction approach based on the modified thermo- dynamic model in Section 3. 3.2. Result Validation In this section, we present the experiment results and assess the performance of the proposed prediction of in- door-temperature for AC scheduling. Model parameters of thermodynamic model calculated by least square al- 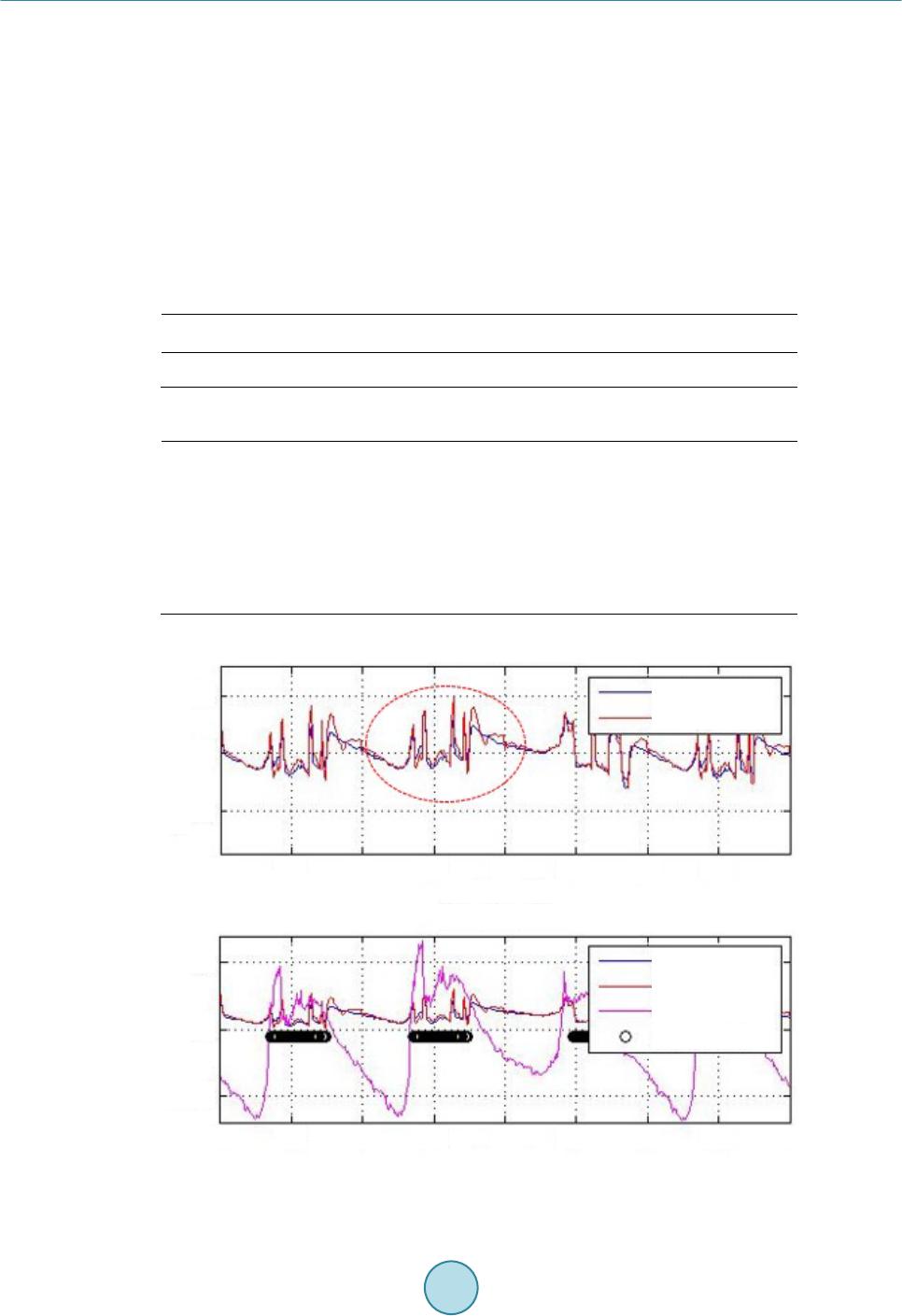 H. D. Choi et al. gorithm are listed in Table 2. The collected data includes AC load consumption, humidity, indoor-temperature and outdoor-temperature within a month period from July 1, 2014 to July 31, 2014. We mainly focus on a three days period due to limited space. After the prediction of next day indoor-temperature, HEMS presents the AC scheduling based on user’s pattern in Table 3. To make the simulation more close to the realistic and show the impact of accuracy of the parameter fitting, real measurement data of indoor-temperature and model based esti- mation of indoor-temperature are plotted for a comparison. The real measurement data of outdoor-temperature, real measurement data of indoor-temperature using AC, predictive indoor-temperature using AC based on con- sume r’s AC usage pattern are shown in Figure 2. Figure 3 shows the PE of indoor-temperature. As shown in Figure 2 and Figure 3, the model-based estimation of indoor-temperature is similar to the measurement data. Forecast of indoor-temperature and AC usage for the next day can be integrated into convex optimization framework for optimal AC scheduling. Table 2. P aramters. (kWh) 0.1176 –2.0121 2 7.1269 0.5081 0 .3 Table 3. AC operating rule based on predictive indoor temperature and humidity. minimum continuous operation hours 20 minutes maximum continuous operation hours 4 hours maximum operating time per day 8 hours The predictive temperature > 27 & humidity < 70% turn on The predictive temperature > 26 & humidity > 70% turn on Figure 2. C o lle cted data and estimation of indoor-temperature. 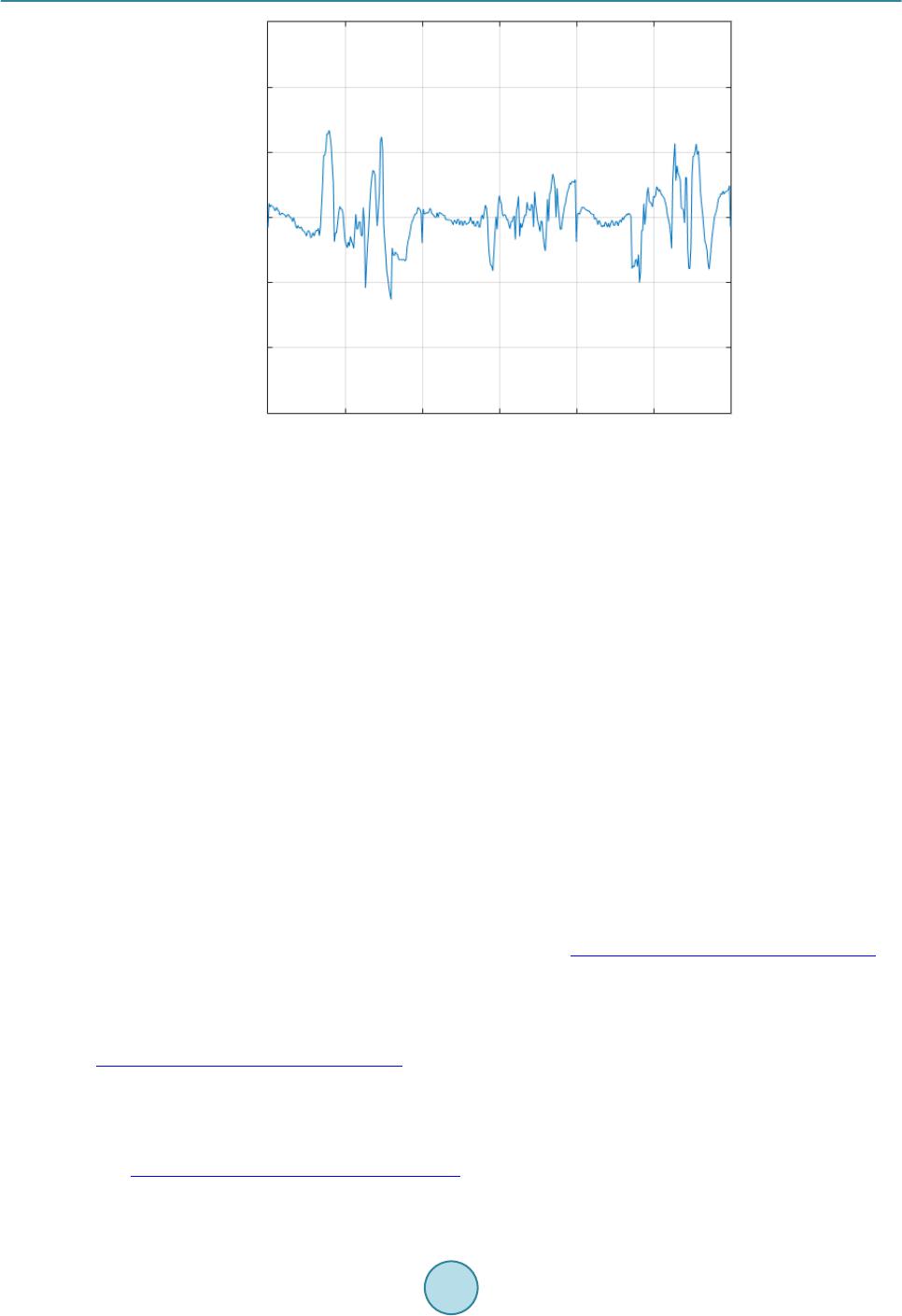 H. D. Choi et al. Figure 3 . Predi ction error (PE) for indoor-temperature. 4. Conclusion In this paper, we implemented HEMS for day-ahead AC scheduling based on thermodynamic model in a labor- atory environment. The AC load forecasting is usually difficult, due to its random nature of turning on/off. The proposed HEMS estimated indoor-temperature based on the modified thermodynamic model and used this in- formation to forecast behavior pattern of AC rather than estimating the AC prediction pattern directly. The case study of the smart AC provides a closed system which is suitable for demonstration purpose in a laboratory en- vironment. The proposed prediction approach based on the modified thermodynamic model can describe ther- mal characteristic of indoor-temperature and can be integrated into the optimization framework for optimal AC scheduling. The ideas described in this paper can be extended to address other thermostatically controlled ap- pliances. Acknowledgements This work was supported by R&D Program of MOTIE/KEIT, Korea. The authors would like to thank the Min- istry of Trade, Industry and Energy, Korea. (No: 10041779, Development of Energy Demand Response System for Smart Home). References [1] Han, D.-M. and Lim, J.-H. (2010) Design and Implementation of Smart Home Energy Management Systems Based on Zigb ee. IEEE Transactions on Consumer Electronics, 56, 1417-1425 . http://dx.doi.org/10.1109/TCE.2010.5606278 [2] Costanzo, G.T., Zhu, G. , Anjos, M.F. and Savard, G. (2012) A System Architecture for Autonomous Demand Side Load Management in Smart Buildings. IEEE Transactions on Smart Grid, 3. [3] Mohsenian-Rad, A. and Leon-Garcia, A. (2010) Optimal Residential Load Control with Price Prediction in Real-Time Electricity Pricing Environments. IEEE Transactions on Smart Grid, 1, 120-133. http://dx.doi.org/10.1109/TSG.2010.2055903 [4] Areekul, P., Senjyu, T., Toyama, H. and Yona, A. (2010) A Hybrid ARIMA and Neural Network Model for Short- Term Forecasting in Deregulated Market. IEEE Transactions on Power Systems, 25. [5] Chen, Y., Luh, P.B. , Guan, C., Zhao, Y., Michel, L.D., Coolbeth, M.A., Friedland, P.B. and Rourke, S.J. (2010) Short- Term Load Forecasting: Similar Day-Based Wavelet Neural Networks. IEEE Transactions on Power Systems, 25, 322 - 330. http://dx.doi.org/10.1109/TPWRS.2009.2030426 [6] Li, B. and Alleyne, A.G. (2010) Optimal On-Off Control of an Air Conditioning and Refrigeration System. Proc. Amer.  H. D. Choi et al. Control Conf., July, 5892-5897. [7] Yu, Z. , McLaughlin, L., Jia, L. , Murphy-Hoye, M.C., Pratt, A. and Tong, L. (2012) Modeling and Stochastic Control for Home Energy Management. Proc. IEEE PES Gen. Meet., July. [8] McLaughlin, L., Jia, L. , Yu, Z. and Tong, L. (2011) Thermal Dynamic for Home Energy Management: A Case Study. Cornell Univ., Ithaca, NY, USA, Tech. Rep. ACSP-TR-10-11 -01. [9] Quiroga, A., Yu, Z. and Tong, L. (2012) Home Energy Management System Thermal Dynamic Model Fitting. Cornell Univ., Ithaca, NY, USA, Tech. Rep. ACSP-TR-09-11-01.
|