 Journal of Power and Energy Engineering, 2015, 3, 215-223 Published Online April 2015 in SciRes. http://www.scirp.org/journal/jpee http://dx.doi.org/10.4236/jpee.2015.34030 How to cite this paper: Noh, F.H.M. , Miyauchi, H. and Yaakub, M.F. (2015) Application of Slantlet Transform Based Support Vector Machine for Power Quality Detection and Classification. Journal of Power and Energy Engineering, 3, 215-223. http://dx.doi.org/10.4236/jpee.2015.34030 Application of Slantlet Transform Based Support Vector Machine for Power Quality Detection and Classification Faridah Hanim M. Noh1,2*, Hajime Miyauchi1, M. Faizal Yaakub3 1Department of Frontier Technology for Energy & Devices, Kumamoto University, Kumamoto, Japan 2Department of Electrical Power Engineering, Universiti Tun Hussein Onn Malaysia, Johor, Malaysia 3Department of Electrical Engineering Technology, Universiti Teknikal Malaysia Melaka, Melaka, Malaysia Email: *han im@ st.c s.ku mamo to-u.ac.jp Received January 2015 Abstract Concern towards power quality (PQ) has increased immensely due to the growing usage of high technology devices which are very sensitive towards voltage and current variations and the de-regulation of the electricity market. The impact of these voltage and current variations can lead to devices malfunction and production stoppages which lead to huge financial loss for the produc- tion company. The deregulation of electricity markets has made the industry become more com- petitive and distributed. Thus, a higher demand on reliability and quality of services will be re- quired by the end customers. To ensure the power supply is at the highest quality, an automatic system for detection and localization of PQ activities in power system network is required. This paper proposed to use Slantlet Transform (SLT) with Support Vector Machine (SVM) to detect and localize several PQ disturbance, i.e . voltage sag, voltage swell, oscillatory-transient, odd-harmon ics, interruption, voltage sag plus odd-harmonics, voltage swell plus odd-harmonics, voltage sag plus transient and pure sinewave signal were studied. The analysis on PQ disturbances signals was performed in two steps, which are extraction of feature disturbance and classification of the dis- turbance based on its type. To take on the characteristics of PQ signals, feature vector was con- structed from the statistical value of the SLT signal coefficient and wavelets entropy at different nodes. The feature vectors of the PQ disturbances are then applied to SVM for the classification process. The result shows that the proposed method can detect and localize different type of single and multiple power quality signals. Finally, sensitivity of the proposed algorithm under noisy con- dition is investigated in this paper. Keywords Features Ex tr acti on, Power Quality Disturbances, Slantlet Transfor m, Support Vector Machine 1. Introduction In recent years, the traditional structures of power system have changed, and the electrical system can no longer  F. H. M. Noh et al. be handled as a single entity. The electricity industry is evolving into a distributed and competitive industry in which market forces drive the price of electricity and reduce the net cost through increased competition [1]. This changes which is known as the deregulation of the electricity industry, has changes the status of electrical power into a product based quantity. These have changed the electricity market to be customer oriented market [1]. On the other hand, the growing usage of high technology devices at the customer side as well as at the generation side had contributes toward the generation of power quality disturbances in the power network. And ironically, all of these equipments are also very sensitive towards power quality disturbances [2]. Owing to the fact that these problems directly affect consumers in production times and costs, nowadays there is a demand by industry for continuous monitoring power systems [3]. Signal processing has been widely used for analyzing power signals for purpose of automatic PQ disturbance recognition. The most widely used signal processing techniques in extracting features of disturbances from a large number of power signals are the fast Fourier transform (FFT) and the windowed Fourier transform which comprises of the short time Fourier transform (STFT) and the wavelet transform [4]. Wavelets have been exten- sively used by the researchers during the last decade due to its capability to decompose signals into frequency- dependent components. It is equivalent to applying a set of subband filters with an octave bandwidth relation, however. The DWTs has been identified as an excellent tool for automatically detecting multiscale singularities in a signal [1]. Recently, SLT has been proved as a better compression technique for PQ data [5]. SLT which has a better time localization as compared to discrete wavelet transform (DWT), is actually an orthogonal DWT with two zero moments. It use a special cases of a class of bases described by Alpert, retains the octave-band characteris- tic and piecewise linear (but discontinuous). The SLT filter is implemented in the parallel structure and each of the filters are not products. Therefore, SLT has extra degree of freedom and lengths of the filter are shorter compare to DWT. In this paper, the applications of SLT in detecting and extracting features of single and mul- tiple power quality disturbances has been investigated. Eight types PQ disturbances signals which are voltage sag, voltage swell, oscillatory-transient, odd-harmonics, interruption, voltage sag plus odd-harmonics, voltage swell plus odd-harmonics, and pure sine-wave signal have been generated using parametric equation and have been analyzed using SLT. In this work, the features are ob- tained from the time-frequency domain data of approximation and details signal of SLT. The standard statistical features and wavelet entropies that have been extracted are max, min, standard deviation, mean, energy entropy and log energy entropy. The result shows that the proposed method can detect and extract several features of different type of single and multiple power quality signals. Finally, sensitivity of the proposed algorithm under noisy condition is investigated in this paper. 2. Methodology 2.1. PQ Data Generation In this paper, the eight types of the PQ disturbance signals have been generated using parametric equations based on the given IEEE Standards 1159-2009 and the equations are given in Table 1. Waveform with 256 cycles at sampling frequency 12.8 kHz have been generated for a total of 65,536 sample points. The fundamen- tal frequency is generated at 50 Hz frequency. 2.2. The Slantlet Transform The SLT was first introduced by Ivan W. Selesnick in 1999 [6]. The SLT is an orthogonal Discrete Wavelet Transform (DWT) with two zero moments, improved time localization, and is based on designing different fil- ters that are not product for each scale [7]. The structure of SLT filter bank depends on the number of scale of SLT that being used. For l-scale SLT filter bank has 2l channels. The first channel consists of filter , followed by filter in the second channel. Both and are to be followed by down sampling by 2l. The remaining 2l-2 channels are filtered by and its shifted time-reverse for . These remaining channels are to be followed by down sampling by [6] . The proposed SLT filter bank in this study use 2-scales and it have 4 channels of filters. The general structure of 2-scales SLT filter bank is shown in Figure 1. The and filters are piecewise linear, hence each filter can be represented as the sum  F. H. M. Noh et al. Table 1. Parametric equation for PQ disturbances signal. PQ Disturbance Signal Generation Equation Parameter Variation Pure Frequency = 50 Hz, A = 1 Sag ( )()() ( ) ( ) ( ) 12 1 sinftAut tut tt αω =−−− − , Swell ( )()() ( ) ( ) ( ) 12 1 sinftAut tut tt αω =+−− − , Interruption ( )()() ( ) ( ) ( ) 12 1 sinftAut tut tt αω =−−− − , Odd-Harmonics ( )()( )( )( ) ( ) 13 5 7 sinsin 3sin 5sin 7 ft Atttt α ωαωαωαω = +++ , , , Oscillatory Transient ()( )( ) ( ) () ( ) ( ) 11 sin expsin oscosc osc ft ttttt ωατ ω =+ −−− , Sag + Harmonic ( )() ( ) () ( ) ( ) ()( )()( ) ( ) 12 13 5 7 1 sin sinsin3sin5sin7 ftAuttut tt tttt αω α ωαωαωαω =−−−− ×+ + + , , , , , Swell + Har monic ( )()() ( ) ( ) ( ) ( )()()() ( ) 12 13 5 7 1 sin sinsin3sin5sin7 ftAuttut tt tttt αω α ωαωαωαω =−−+− ×+ + + , , , , of a DC and a linear term. The general equation of , and are given as follow [6]: ()( ) 0,0 0,1 1 1,01,1 ,for 0,,21; 1,for 2 ,,21. i iii a ann gn a ann + +=− =+−=− (1) ( )( ) 0,0 0,1 1 1,01,1 ,for 0,,21; 1,for 2,,21. l lll b bnn hn bbnn + +=− =+−= − (2) ()() 0,0 0,1 1 1,01,1 ,for 0,,21; 1,for 2,,21. l lll c cnn fn c cnn + +=− =+−= − (3) The SLT filters fulfilled the following conditions in order to have the orthogonality and zero moment condi- tions [3]: 1) The SLT filters are off to unit norms. 2) They are orthogonal to theirs shifted time reverse. 3) The and filters annihilate linear discrete time polynomials. Now since the coefficient of each filter is orthogonal to its corresponding shifted time-reversal while preserv- ing their piecewise linear characteristics, a satisfactory computation performance can be also ensured. As stated by [7], it is observed that SLT fulfilled most of the properties for PQ event analysis. This is because the SLT consist of oscillatory function so that analysis on oscillated signal can be performed. It also has short support of filter and has two vanishing moments which can be used to reduce the number of coefficient to be analyzed [7]. In this study, the features of the PQ disturbances have been extracted from all of the decomposition level of SLT filterbank. 2.3. Support Vector Machine Support Vector Machines is a powerful methodology for solving problems in nonlinear classification, function  F. H. M. Noh et al. Figure 1. The structure of 2 scales SLT filterbank. estimation and density estimation in kernel based methods in general [8]-[10]. The basic idea is to find a hyper- plane which separates the d-dimensional data perfectly into its two classes. Given the training data (x1, y1) … (xl, yl), , where each data consists of M features. These features describes for a two-class problem as: (4) The SVM constructs the decision function given as, , where w is the optimal solution and b is the bias parameter. These parameters are derived to classify the data correctly. An important concept in SVMs is the margin. A margin of a classifier is defined as the shortest distance between the separating boundary and an input training vector that can be correctly classified. For a soft-margin SVM, support vectors can lie on the mar- gins as well as inside the margins. A soft-margin SVM is described as a quadratic optimization problem: 2 ,, 1 1 min 2 N i wb i wC ξ ξ = + ∑ (5) where is a user-specified regularization parameter that determines the trade-off between the upper bound on the complexity term and the empirical error [8]. If there were a “kernel function” K such that K , then only K is used in training algo- rithm, and never need to explicitly determine φ. Thus, kernel is a special class of function that allows inner products to be calculated directly in feature space. In this paper, the application of radial basis function (RBF) kernel has been used in order to classify the single and multiple PQ disturbance signals. The RBF kernel has been defined as in Equation (6). (6) where is the width parameter of RBF function. The accuracy of the selected SVM relies on the selection of the kernel parameter, , and the regularization parameter, . The proper value of will give higher classification rate and reduce the processing time [9]. The parameters should be determined prior to the training process. In this paper, parameters and were chosen using 5 cross validation technique. 2.4. Features Extraction The coefficient of at all decomposition levels are used to extract the feature of different type of PQ distur- bances. Statistical feature and wavelet entropy like mean, maximum, minimum, standard deviation, energy and log energy entropy of the decomposition coefficient of are calculated using the equations in Table 2 [10] . 2.5. The Overall Framework In this study, the use of the 2 scales SLT filter bank has been proposed. It consist of 4 channels of filters, which are , , and its shifted time reverses. The parameter values of the filters are calculated using Equations (1)-(3). The process flow of extracting features with the application of 2 scales SLT filter bank are given in Fig ure 2. The process starts by applying the PQ signal for the transformation. Then the process of thresholding is done in which suitable threshold is chosen for discarding the SLT coefficients which are not having significant energy. 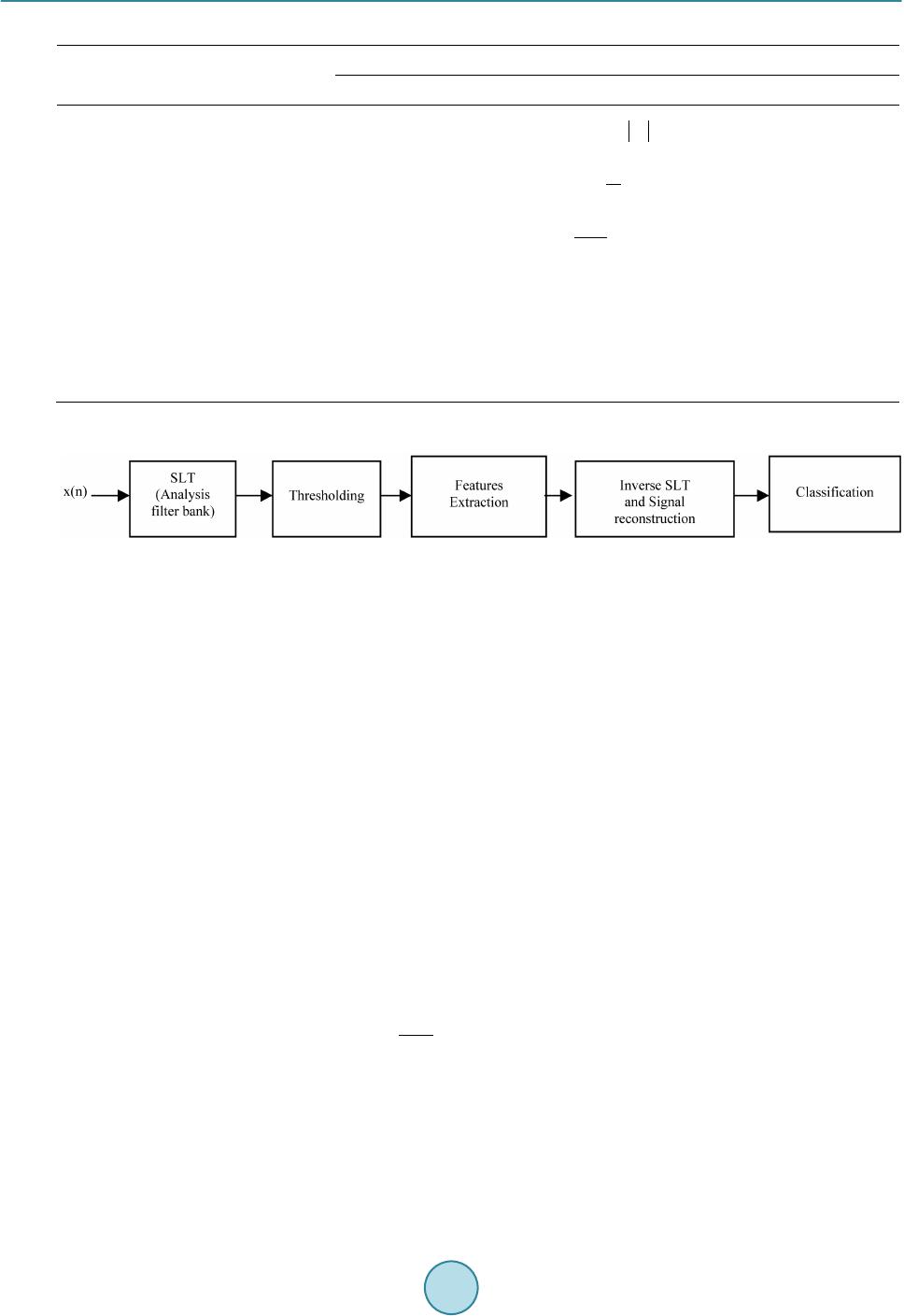 F. H. M. Noh et al. Table 2. Equation for features of PQ disturbances. Features Features Extraction Equation Energy Mean Standard Deviation ( ) 2 1 1 1 N ijij ij j D N σµ = = − − ∑ Minimum Maximum Log Energy Entropy a is the number of decomposition scales, while represent the number of coefficient for each decomposition level. Figure 2. The overall process flow of PQ detection and classification using SLT based SVM. The output signal from the analysis filterbank after the thresholding process, i.e. d1, d2, d3 and d4, will then be analyzed and processed so that several feature of PQ event can be extracted. These features will be used in clas- sification system to identify the type of disturbance that exists in the given signals. Then the signal will be transform again by using inverse SLT/synthesis filterbank in order reconstructed original signal. Based on the constructed signal, the effectiveness of the thresholding process can be observed. The wavelet thresholding process has been applied to the SLT coefficient signals in order to de-noised the noisy signals. The threshold method for SLT coefficient that being used in this paper are hard threshold rule with Ri- gorous SURE (RigSURE) and Heuristic SURE (HeurSURE) threshold selection method. 3. Result and Analysis Figure 3 shows PQ signals generated based on the given parametric equation in Table 1. In this study, the appli- cations of 2 scale SLT filters to analyze PQ disturbance signals have been performed. Similar to wavelet trans- form, SLT deals with expansion of function in terms of a set of basic function which allowed the signals to be analyzed in time and frequency domain. The signal generated in wavelet domain will give some information due to the existence of disturbances in the signal and the duration of the disturbances. Figure 4 sho ws the output signal of 2 scale SLT synthesis filterbank for single PQ disturbance signal. Figures 4(a) -(c) show the capabilities of SLT to detect single PQ disturbance signal at different frequency level. Center frequency for each SLT filterbank is calculated using Equation (7) [1] and the values are given in Table 3. (7) where is the sampling frequency and M is the total number of scales. represents the center frequency of the highest scale or high pass filter of SLT (g1(n)) and is the center frequency of the lowpass filter of SLT . In this study, the harmonic signals contain odd harmonics components, which are the third, fifth and seventh harmonics component. Since the harmonic component is in the range of 150 Hz to 350 Hz, the detection of the harmonic can be seen in the output filter of , along with the fundamental component of the signals. How- 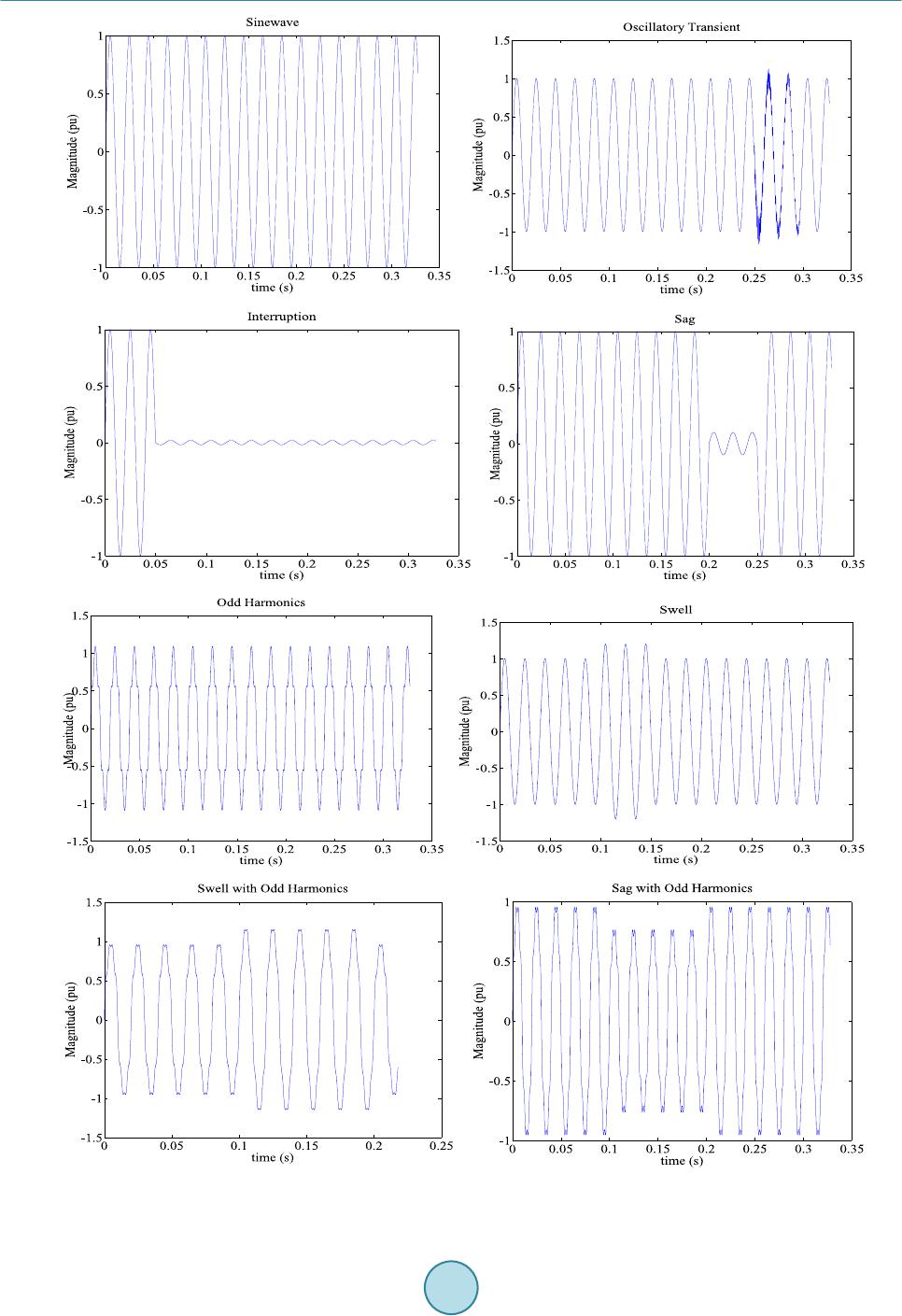 F. H. M. Noh et al. Figure 3. Generated signal using parametric equation.  F. H. M. Noh et al. ever, as for higher frequency component of PQ signals, such as transient signals in Figure 4(c) , the existence of the transient component can only be seen at the output signal of filter , as well as filter . Detection of multiple PQ disturbances is shown in Figures 5(a)-( b). RBF support vector machine have been utilized to classify all these eight types of PQ disturbance that have been studied in this paper. The classification process is made in Matlab2009a environment and 150 signals for each type of PQ disturbances have been generated using parametric equation in Table 1. The training and testing data are divided by using 1/3 distribution, which mean 2/3 of the generated signals will be used for training, and the rest will be used as testing data. Total of 6 × 4 × 150 × 8 features have been extracted from the simulated PQ signals. By using five cross validation technique, the optimized value of C and γ have been determined iteratively. In order to verify the robustness of the proposed method, several PQ signal added with AWGN with SNR 20 dB, 25 dB and 30 dB have been feed to the proposed PQ detection and classification system. RigSURE and Heur- SURE threshold selection method combined with hard threshold techniques have been applied to SLT coefficient signals. The results are shown in Table 4. (a) (b) (c) Figure 4. SLT signal coefficient for single PQ disturbance signal. (a) Sag; (b) Harmonics; (c) Tran s i en t. (a) (b) Figure 5. SLT signal coefficient for multiple PQ disturbance signal. (a) Sag and harmonics; (b) Sag and transient.  F. H. M. Noh et al. Table 3. Center frequency for SLT filters. Filter Center Frequency h2(n) 1200 Hz f2(n) 2400 Hz g1(n) 4800 Hz aThe shifted-time reverse filter of g1(n) has the same center frequency with g1(n). Table 4. Classification results. PQ Signals Classification Accuracy SLT + SVM SLT + RigS URE + SVM SLT + HeurSURE + SVM Clean Signals 98% - - 20 dB AWGN - 70% 79% 25 dB AWGN - 75% 81% 30 dB AWGN - 79% 87% 4. Conclusion The application of 2 scales SLT filter has been studied and analyzed. According to the simulated result, it is ob- served that the 2 scales SLT capable to detect the single and multiple PQ disturbance signals with precise time localization. The extracted statistical and wavelet entropy data gives unique values and trend for different type of PQ disturbances signals, which are suitable for event identification. However, with the existence of noises in the signals, the performance of the proposed techniques degraded. This shows that the studied features of PQ signals varied or destroyed with this AWGN. Thus, more robust features for PQ disturbance signals should be proposed in future. Acknowledgements The authors wish to thank Ministry of Education Malaysia and Kumamoto University for providing resources and financial support for this research. References [1] Bollen, M.H.J. and Gu, I.Y.H. (2006) Signal Processing of Power Quality Disturbances. IEEE Press Series on Power Engineering, John Wiley & Sons Inc., Hoboken. http://dx.doi.org/10.1002/0471931314 [2] Thapar , A., Saha, T.K. and Dong, Z.Y. (2004) Investigation of Power Quality Categorisation and Simulating It’s Im- pact on Sensitive Electronic Equipment. IEEE Power Engineering Society General Meeting, 1, 528 -533. [3] Gra nados -Lieberman, D., Romero-Troncoso, R.J., Osornio-Rios, R.A., Garcia-Pere z, A. and Cabal-Yepez, E. (2011) Tech- niques and Methodologies for Power Quality Analysis and Disturbance Classification in Power System: A Review. IET Generation Transmission & Distribution, 5, 519-529. http://dx.doi.org/10.1049/iet-gtd.2010.0466 [4] Moussa, A., El-Gammal, M., Abdallah, E.N. and El-Sloud, A.A. (2004) Hardware-Software Structure for On-Line Po- wer Quality Assessment. Proceedings of the 2004 ASME/IEEE Joint, Baltimore, 8 April 2004, 147-15 2. http://dx.doi.org/10.1115/RTD2004-66022 [5] P anda, G., Dash, P.K.A., Pradhan, K. and Meher, S.K. (2002) Data Compression of Power Quality Events Using the Slantlet Transform. IEEE Transactions on Power Delivery, 17, 662-667. http://dx.doi.org/10.1109/61.997957 [6] Selesnick, I.W. (1999) The Slantlet Transform. IEEE Transactions on Signal Processing, 47, 1304-1313. http://dx.doi.org/10.1109/78.757218 [7] Meher, S.K. (2008) A Novel Power Quality Event Classification Using Slantlet Transform and Fuzzy Logic. Proceed- ing of Power System Technology and IEEE Power India Conference, New Delhi, 12-15 Octob er 2008, 1-4. http://dx.doi.org/10.1109/ICPST.2008.4745234 [8] Burges, C.J.C. (1998) A Tutorial on Support Vector Machine Pattern Recognition. Data Mining and Knowledge Dis- covery, 2, 121-167. http://dx.doi.org/10.1023/A:1009715923555  F. H. M. Noh et al. [9] V apni k, V.N. (2000) The Nature of Statistical Learning Theory. 2nd Edition, Springer-Verlag, New York. [10] Cortes, C. and Vapnik, V.N. (1998) Support Vector Network. Machine Learning, 20, 121 -167 .
|