 Journal of Power and Energy Engineering, 2015, 3, 155-161 Published Online April 2015 in SciRes. http://www.scirp.org/journal/jpee http://dx.doi.org/10.4236/jpee.2015.34022 How to cite this paper: Chen, C.Y., Hu, B.W. and Wang, X.R. (2015) Simulation Study on Electromechanical Disturbance Propagation in Large Power System. Journal of Power and Energy Engineering, 3, 155-161. http://dx.doi.org/10.4236/jpee.2015.34022 Simulation Study on Electromechanical Disturbance Propagation in Large Power System Changyong Chen, Bowei Hu, Xiaoru Wang School of Electrical Engineering, Southwest Jiaotong University, Chengdu, China Email: 592199530@qq.com, 409134117@qq.com, xrwang@swjtu.cn Received January 2015 Abstract Power systems are subjected to all kinds of random disturbances, showing the electromechanical dynamic. A lot of theoretical researches show that the disturbance power and frequency is propa- gating in the form of wave which is called electromechanical wave. But electromechanical wave theory is not widely used in ac tu al power system. In this paper we focus on simulation study of electromechanical wave frequency sensitivity and propagation velocity and elaborati ng the simu- lation results with the electromechanical wave theory. Finally some summaries and expectations on electromechanical wave study are made. Keywords Electromechanical W av e, Power Sys tem, Simulation Study, Frequency Sensitivity, Propagation Velocity 1. Introduction People had already been aware that frequencies change differently in different measuring points of power sys- tem when there were electromechanical disturbances. For example in Western Europe United power system, people found that times needed for frequencies to reach their maximum values were different in different mea- suring points, according to which people estimated the velocity of frequency disturbance propagates in power system [1] [2]. With the development of PMU technology, people are able to observe different frequencies change in different locations. In Sichuan power grid, with the help of three sets of FNTE installed in Chengdu Panzhihua and Chongqing people found that frequencies in Chengdu Panzhihua and Chongqing are temporally and spatially distributed during the 5.12 earthquake [3]. In References [4] [5], the author studied the frequency sensitivity and electromechanical disturbance propagation velocity in Eastern United States power grid and the United States power grid. Similarly in this paper we study the frequency sensitivity and electromechanical dis- turbance propagation of an actual power system in China basing on simulations. We apply perturbations in dif- ferent locations and observe the difference of disturbance arrival times in different measuring points. According to the spatial distances and arrival times of the electromechanical disturbance, we calculate the velocities of the 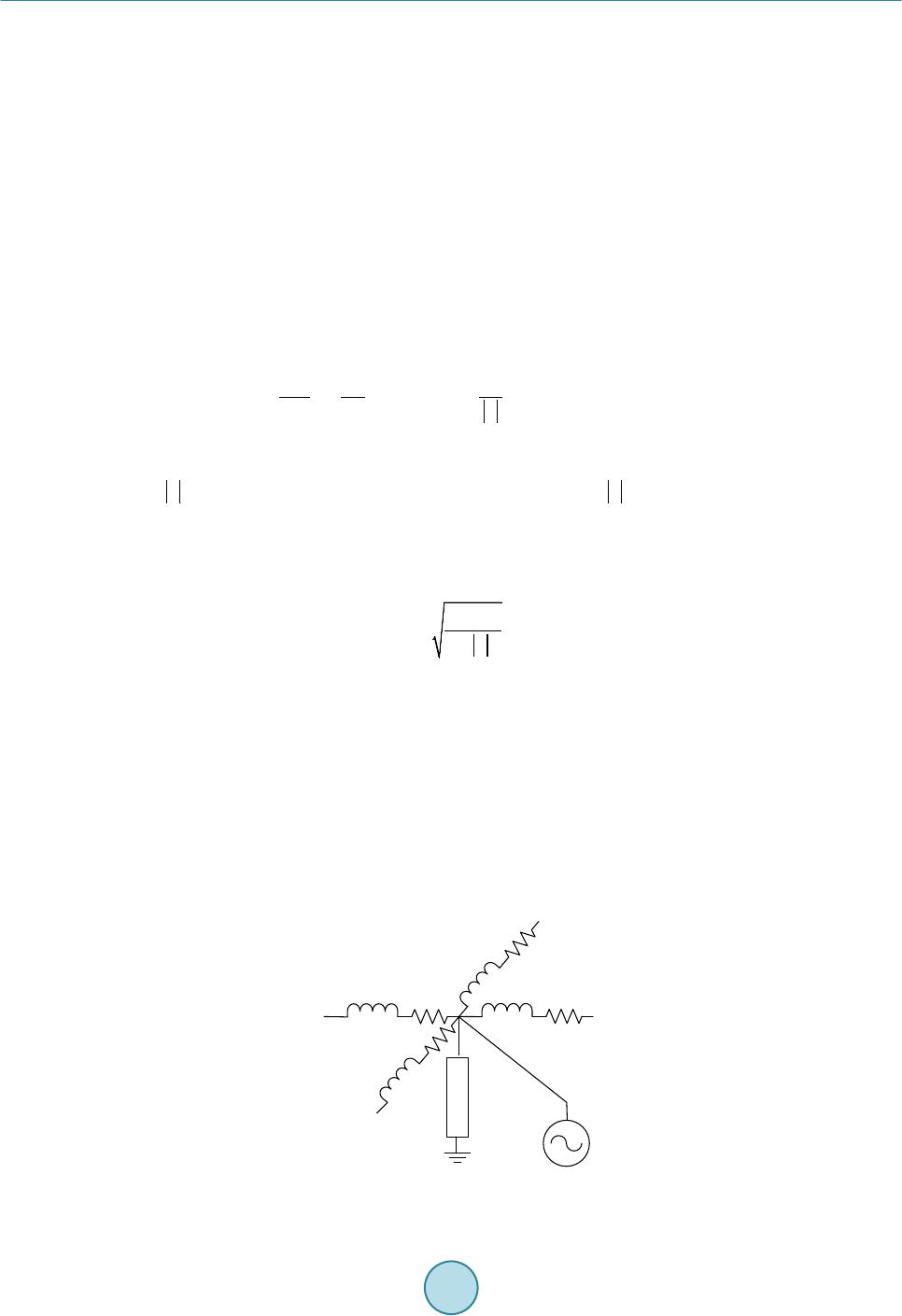 C. Y. Chen et al. electromechanical disturbance in this power grid. This paper is organized as follow: in Section 2, some electro- mechanical wave theories introduced, in Section 3 the simulation study on frequency sensitivity and velocity of electromechanical wave in the actual power grid are measured, Section 4 is summaries and prospects on elec- tromechanical wave. 2. Theoretical Background Electromechanical wave theory is to study the electromechanical disturbance propagation in continuum method. References [6]-[15] show the study on electromechanical wave’s propagation and control. Modern large-scale powers are composed of tens of thousands of nodes that are discrete distributed. Such as Sanhua Grid of China, which across half of China, is the connection of various power system components and physically connected by transmission lines. In essence, the actual power system may not be spatially continuous uniform system, but a spatially discrete distributed non-uniform system. Figure 1 shows a distributed discrete power system. In power system continuum modeling, the generator excitation, governor and some other dynamic compo- nents are not concluded, and assume that gennerator bus voltages remain constant. In reference [10] the wave equation of generator power angle is given as follow () 22 2 22 2 sin cos ms V mdp GV tz t δδ θδθ δ ∂∂ += −−∇+∇ ∂ ∂ (1) Quantities in the equation are all in per unit values, δ is the power angle of generator, m is the generator iner- tia time constant per unit length, V is bus voltage which is often assumed to be 1, z is the line impedance of per unite length, is line impedance modulus per unite length and ( ) cos sinzzjr jxz θθ = +=+ , where r is line resistance per unit length, xz is line reactance per unit length, pm is the generator mecha nic al input per unit length, Gz is conductance value to ground per unit length. Electromechanical wave propagates in certain velocity, which is more slowly than that of light, in Reference [10] electromechanical wave velocity is given as following according to Equation (1). (2) We can conclude from Equation (1) that electromechanical velocity is inversely proportional to the square root of generator inertia time constant per unit length, which means in the area where generator inertia time con- stant is denser the electromechanical wave propagates slower. In general the generator inertia time constant represents the time that the generator needs to achieve rated speed from the stationary state. The bigger the ge- nerator inertia time constant is the longer time the generator needs to response to the disturbance, which is help- ful for the prevention of electromechanical wave propagation. Electromechanical wave velocity is inversely proportional to the square root of the line impedance per unit length, which means the bigger the line impedance is the slower the electromechanical wave propagates. In actual discrete power system, generators are not spatial continuous, thus the electromechanical velocity we study in this paper is the velocity the electromechanical dis- turbance propagate from one point to the other point. Figure 1. A distributed discrete power system. 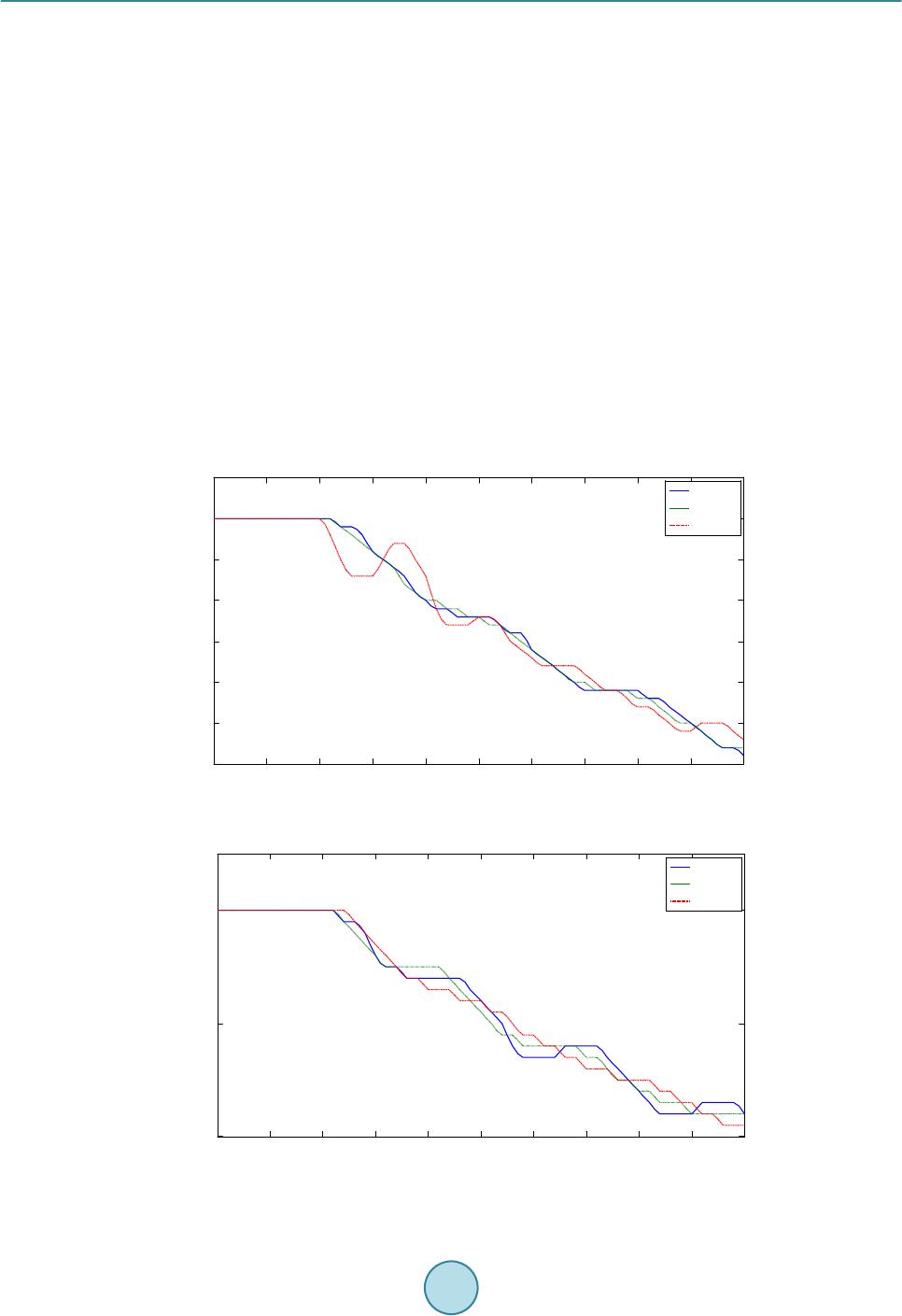 C. Y. Chen et al. 3. The Simulation Study on Frequency Sensitivity and Velocity of Electromechanical Wave 3.1. Research on Frequency Sensitivity Based on Simulations In this paper, power system analysis synthesize program (PSASP) is chosen as the simulation tool and system baseline capacity is chosen as 100 MW, the simulation time step is 0.01 seconds. The simulation time is 5 seconds and cutting machine operation is performed in 1 second. In the simulation, the governors detect distur- bance and act about 2 seconds later generally when taking no account of generator excitation and governors. The data within 2 seconds after the disturbance is concerned only because the governors begin to move 2 seconds later. Due to the governor, the generator mechanical power input is adjusted and the electromechanical wave propagation is affected significantly. When the frequency variation of the whole network that exceed 0.05 Hz which all over the 500 kV bus and all the generators, the disturbance spread throughout the network and cause the whole network frequency perturbations under the amount of cutting machine or cutting load. In this paper, a large number of simulations in the system are completed. And the system frequency response curves after cutting generators are shown in Figure 2. T he frequency response curves when cut PT#02 genera- tors (0.6pu), DJP#2 (0.43pu) and FYB2# generators (0.21 pu) are shown in Figure s 2-4. The frequency varia- tions of the whole network are compared in the actual simulation process. Figure 3 shows three significant ge- nerators’ frequency response curves. DY power plant is in the border of SX and CQ in DZ city, and DN hydro- power station is in the border of CB and GS in AB while TZL hydropower station is in the south of the Figure 2. The system frequency response curves when cut PT#02 generator. Figure 3. The system frequency response curves when cut DJP #2 generator. 00.5 11.5 22.5 33.5 44.5 5 0.9997 0.9997 0.9998 0.9998 0.9999 0.9999 1 1 t/s Frequency(pu) DY#31 D N1# TZL#01 00.5 11.5 22.533.5 44.5 5 0.9998 0.9999 1 t/s frequency(pu) DY#31 D N1# TZL#01  C. Y. Chen et al. Figure 4. The system frequency response curves when cut FYB#2 generator. province in YBX. When the system disturbance occurs, if these three units within 2 seconds felt the disturbance occurred, which can be determined that the disturbance occurred within 2 seconds throughout the whole net- wor k . As can be seen from Figure 5, the frequency response curves of DY#31, DN1# and TZL#01 generators exhi- bits different characteristics when the active power of the generator which is cut is not the same. When the ac- tive power of cutting generator is less than 0.43 pu, the system has at least 1 generator within 2 seconds after the disturbance occurs which frequency variation is less than 0.005 Hz (that is 0.0001 pu), namely the disturbance cannot spread the whole network within 2 seconds after the disturbance occurs. And 2 seconds later, the output of the system is increased and the frequency dynamic of the system is affected because of the action of the gov- ernor. The above can be explained as that the sensitivity of different the amount of cutting generators is different. Only a minimum of cutting generators are reached, the frequency variation in the system can exceed the set threshold, and the disturbance occurs in the whole network. Obtain the power generation of an actual power grid through steady trend data. The power generation is about 698.22 pu and the minimum percentage of cutting generator accounted for a total generating capacity of the ac- tual grid is approximately 0.0616%. 3.2. Research on System Frequency Wave Propagation Velocity As can be seen from Figure 2, in the case of the same size of the disturbance, times tha t frequency variation of DY#31 generator, DN1# generator and TZL#01 turbine generator reach 0.005 Hz are different. That is to say, frequency wave is spread in the system, rather than the instantaneous to arrive. According to Equation (2), elec- trical wave propagation velocity in the system is inversely proportional to the square root of the multiply of the inertia time constant per unit length and per unit length line reactance. The greater the inertia time constant and per unit length line reactance place, the slower electromechanical wave propagation velocity, and vice versa, the faster. Making use of electromechanical wave propagation velocity, the density of generator and per unit length line reactance can be estimated roughly. Using a linear distance between 2 points measured on the map and di- vided by the time of arrival of the disturbance when estimating the electromechanical wave propagation velocity. That is: (3) where is a distance measured between two points on the map; And is the time of arrival of the dis- turbance. The electromechanical wave propagation velocity in CDM power grid and in South of this gird are compared. When estimated the frequency wave propagation velocity in CDM gird, the WWS81 generator is cut which the 00.5 11.5 22.5 33.5 44.5 5 0.9999 1 t/s Frequency(pu) DY#31 D N1# TZL#01  C. Y. Chen et al. output active power is 1.2 pu, and the angular frequency variation of CJY#31 generator and frequency variation of bus CDYII500 and CXD500 are measured. The frequency response curves in CDM grid when cut WWS81 generator is shown in Figure 5, and the frequency wave propagation velocity in CDM grid is shown in Table 1. When estimated the electromechanical wave propagation velocity in CN gird, the HMK#11 generator is cut shows in Figure 6 which the output active power is 1.2 pu, and the angular frequency variation of XJB#1 gene- rator, CET#01 generator and XLD#01 generator are measured. The frequency response curves in CN grid when HMK#11 generator is cut is shown in Figure 6, and the frequency wave propagation velocity in CN grid is shown in Table 2. As can be seen from the above data, the frequency wave propagation velocity in CN grid is slower than elec- tromechanical wave propagation velocity in CDM grid, and the reasons are as follows. There are a large number of hydropower stations in CN (such as PZH, YB and LS) while there are a small number of power stations in CDM (such as ZPP and JY). What’s more, the power grid in CN is more spared than power grid in CDM, and the equivalent per unit length line reactance is larger so that the electromechanical wave propagation velocity is slower according to the equation. To sum up, the density of regional power generators and the tightness between generators and grid can get a rough estimate by measuring the regional power grid electromechanical wave propagation velocity. 4. Summaries and Prospects The frequency sensitivity and frequency wave propagation velocity are researched in a real power grid with Figure 5. The frequency response curve when cut WWS81 generator. Figure 6. The system frequency response curves when cut HMK#2 generator. 00.5 11.5 22.5 33.5 44.5 5 0.9997 0.9999 1 t/s Frequancy(pu) JY#31 DYII500 XD500 00.5 11.5 22.5 33.5 44.5 5 0.9998 0.9999 1 t/s Frequency(pu) XJBZ#1 ET#01 XLD#01 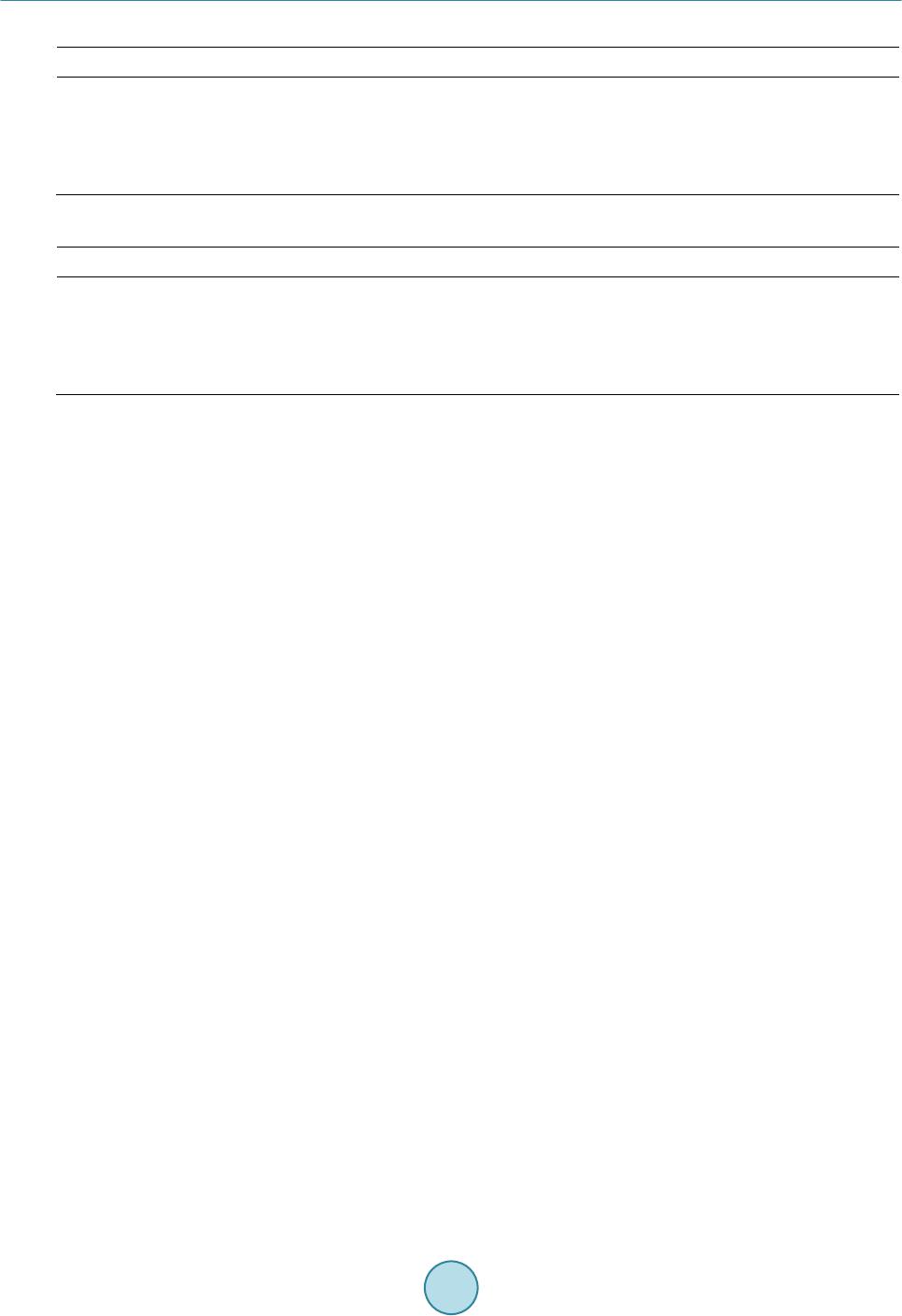 C. Y. Chen et al. Table 1. The frequency wave propagation velocity in CDM grid. Distance to the disturbance point (k m) Arrival time (s) Wave velocity (km/s) CJY#3 1 290 1.02 284 CD Y II5 0 0 2 07 0.85 243 CXD500 170 0.85 200 Average velocity 242 Table 2. The frequency wave propagation velocity in CN grid. Distance to the disturbance point (k m) Arrival time (s) Wave velocity y (km/s) CJY#3 1 290 1.02 284 CD Y II5 0 0 2 07 0.85 243 CXD500 170 0.85 200 Average velocity 242 PSASP in this paper. It was found that the frequency response curves appear broken line because the perturba- tion is small and the decimal digits are retained. But overall, there is little effect on the experiment. A certain minimum amount of cutting generators is studied when the frequency variation reaches 0.005 Hz in the actual power grid. The frequency variation of the bus is greater than 0.005 Hz within 2 seconds after the disturbance when the active power of cutting generator reaches approximately 0.43 pu and the cutting generators accounted for 0.0616% in 2014 to a total of actual power generating capacity. Comparing the electromechanical wave propagation velocity in CDM power grid with in CN power grid, it’s found that the electromechanical wave propagation velocity is slow in the power grid which connection is weak and generator density is great. And the density of regional power generators and the tightness between generators and grid can get a roughly estimate by the electromechanical wave propagation velocity. Here are some summaries and prospects on electromechanical wave study. The goal of modeling of the power system electromechanical wave propagation and building the electrome- chanical wave propagation equation is to study the power system in a different perspective, providing a new method for power system analysis and control. In the existing references on electromechanical wave theory, there are many hypotheses for power systems that were studied. Such as the bus voltage is assumed to be con- stant. And there are a lot of factors that are neglected when modeling of the system. Moreover, the existing re- search findings on electromechanical wave are almost theoretical research; there are a lot of shortcomings in practical application. • In electromechanical wave research, people are mostly concentrated on modeling research; there are little research on practical application. Seldom do they use electromechanical wave theory to explain practical phenomena. Take low frequency oscillation in power system as example, although a small amount of exist- ing literatures have studied about it. They said that the low frequency oscillation is result from the multiple reflection of electromechanical wave, but they are not able to explain the increasing amplitude oscillation. • Controller design based on electromechanical wave theory, mainly focused on the design of the controller algorithm, and the controllers are often tested in ideal systems. For actual power system, the design of con- troller basing on electromechanical wave theory, they borrow the electromechanical wave ideas only. There is little further research on controller design based on electromechanical wave theory. In controller design, continuum modeling is very important. Different continuum modeling methods result in different electro- mechanical impedance, which makes a big difference in precision of controller design. Therefore it is of importance for controller design basing on electromechanical wave theory to find a better way to the conti- nuum modeling of power networks. • In the existing electromechanical wave researches, there are a lot of simplifies in power system modeling. The electromechanical dynamic of generator governor, exciter and FACTS equipments are often ignored. However, these devices play important roles in the propagation of electromechanical wave. Let take speed governor for example, it will change the active input power of the generator’s prime mover, so as to change  C. Y. Chen et al. the generator’s active output power, power angle and angular frequency. Therefore, how to take more dy- namic equipments into consideration in continuum modeling, so as to make the electromechanical wave theory more approximated to the actual power grid, is also one of difficulties in electromechanical wave study. References [1] Han, Y.D. (1989) Mid-Term Stability of Electrical Power System and the Investigation with the Aid of Equivalent Non- Uniform Line (I)—Exponential Line. Journal of Tsinghua University, 19, 1-10. [2] Han, Y.D. (1989) Mid-Term Stability of Electrical Power System and the Investigation with the Aid of Equivalent Non- Uniform Line (II)—Bassel Line. Journal of Tsinghua University, 19, 11-18. [3] Wan g, X.R. and Liu, Y.L. (2010) Analysis of Frequency Dynamics in Large-Scale Power Systems. Southern Power System Technology, 4, 11-17 . [4] Tsa i, S.S., Zhang, L., Phadke, A.G., et al. (2004) Study of Global Frequency Dynamic Behavior of Large Power Sys- tems. Proceedings of 2004 IEEE PES Power Systems Conference and Exposition, New York, 10-13 Octob er 2004 . [5] Tsai, S.-J., Zhang, L., Phadke, A. G. , et al. (2007) Frequency Sensitivity and Electromechanical Propagation Simulation Study in Large Power Systems. IEEE Transactions on Circuits and Systems I: Regular Papers, 54, 1819-1828. http://dx.doi.org/10. 1109 /TCS I. 200 7.90 25 42 [6] Wan g, D.L. (2007) Study on the Continuum Electromechanical Wave Model and Electromechanical Disturbance Pro- pagation in Power Systems. Southwest Jiaotong University, Chengdu. [7] Seml yen, A. (1974) Analysis of Disturbance Propagation in Power Systems Based on a Homogeneoue Dynamic Model. IEEE Transactions on Power Apparatus and Systems, 93, 676-684. http://dx.doi.org/10.1109/TPAS.1974.294030 [8] Cresap , R.L. and Hau er, J.F. (1981) Emergence of a New Swing Mode in the Western Power System. IEEE Transac- tions on Power Apparatus and Systems, 100, 2037-20 45. http://dx.doi.org/10.1109/TPAS.1981.316481 [9] Hauer , J.F. and Cresap R.L. (1981 ) Measurement and Modeling of Pacific AC Intertie Response to Random Load Switching. IEEE Transactions on Power Apparatus and Systems, 100, 353 -359. http://dx.doi.org/10.1109/TPAS.1981.316863 [10] Thorp, J.S., Seyler, C.E. and Phadke, A.G. (1998) Electromechanical Wave Propagation in Large Electric Power Sys- tems. IEEE Transactionson Circuits and Systems I: Fundamental Theory and Applications, 45, 614 -622. http://dx.doi.org/10.1109/81.678472 [11] Parash ar, M., Thorp, J.S. and Seyler, C.E. (2004 ) Continuum Modeling of Electromechanical Dynamics in Larg e-Scale Power Systems. IEEE Transactions on Circuits and Systems I: Regular Papers, 51, 1848-1858 . http://dx.doi.org/10.1109/TCSI.2004.834480 [12] Manu, P. (2003 ) Continuum Modeling of Power Networks. Cornell University, Ithaca. [13] Wang, D.L. an d Wan g, X.R. (2012) Electromechanical Disturbance Propagation and Oscillation in Power Systems. 2012 IEEE Power and Energy Society General Meeting, 22 -26 July 2012, San Diego. [14] Thomas, A.J. and Mahajan, S.M. (2009) Electromechanical Wave Analysis through Transient Magnetic Modeling. IEEE Transactions on Power Delivery, 24, 2336-2343. http :/ /dx. doi.o rg/ 10. 11 09/ TP WRD.20 09 .20 275 04 [15] Scott, B. and Liu , Y.L. (2012) Electromechanical Wave Green’s Function Estimation from Ambient Electrical Grid Frequency Noise. 45th Hawaii International Conference on System Science (HICSS), Ma u i, 4-7 Januar y 2012.
|