 Journal of Power and Energy Engineering, 2015, 3, 106-113 Published Online April 2015 in SciRes. http://www.scirp.org/journal/jpee http://dx.doi.org/10.4236/jpee.2015.34016 How to cite this paper: Liu, J., Duan, J.D., Lu, H.L. and Sun, Y.B. (2015) Fault Location Method Based on EEMD and Travel- ing-Wave Speed Characteristics for HVDC Transmission Lines. Journal of Power and Energy Engineering, 3, 106-113. http://dx.doi.org/10.4236/jpee.2015.34016 Fault Location Method Based on EEMD and Traveling-Wave Speed Characteristics for HVDC Transmission Lines Jing Liu, Jiandong Duan, Hailong Lu, Yuanbing Sun Department of Electrical Engineering, Xi’an University of Technology, Xi’an, China Email: duanjd@xaut.edu.cn Received Dec emb er 2014 Abstract This paper presents a method of Traveling Wave Fault location based on the improved Hilbert- Huang Transform. First, Intrinsic Mode Functions (IMF) of traveling waves are extracted by En- semble Empirical Mode Decomposition (EEMD). Then Hilbert Transform is applied to calculate the correspondi ng ins tant aneous f reque ncy of the h ighest frequ ency component (IMF1), the instan- taneous frequency and corresponding time-frequency graph are obtained. Second, the arrival time and speed can be detected by the first instantaneous frequency’s mutational point. Finally, the improved two-terminal traveling wave fault location principle is used to calculate the fault dis- tance. Relevant simulation results are performed to verify the correctness of the method by EMT DC so ftwa re. Keywords Traveling Wave, Fault Location, EEMD, Instantaneous Frequency 1. Introduction The long-distance transmission and complex environment of the transmission line are not only the main charac- teristics of the HVDC system, but also are the reasons for the shutdown of the HVDC system. Traveling wave fault location is one of the common used techniques for fault location in a DC line. However, the traveling wave fault location is affected by the arrival time, wave speed, and other factors [1]-[3]. Wavelet analysis and other signal processing methods are used to extract the fault traveling wave head, and to improve the acc uracy of wave head [4]. In theory, wavelet analysis has several wavelet bases. It’s hard to get a satisfactory result if wavelet base is selected improperly [5], while wavelet analysis does not have ad ap tab ilit y in data process [6 ]. Thi s limits the application of wavelet analysis in the electric power system greatly. The fault step wave includes a spectrum which contains frequency components from zero to infinity. In the literature [7], the lower is the frequency components are, the slower the wave speed; The farther the fault dis- tance is, the more serious are the dispersion characteristics of the fault traveling wave. That means with different fault distance, the high frequency component of the fault wave head detected in the measuring point is different. 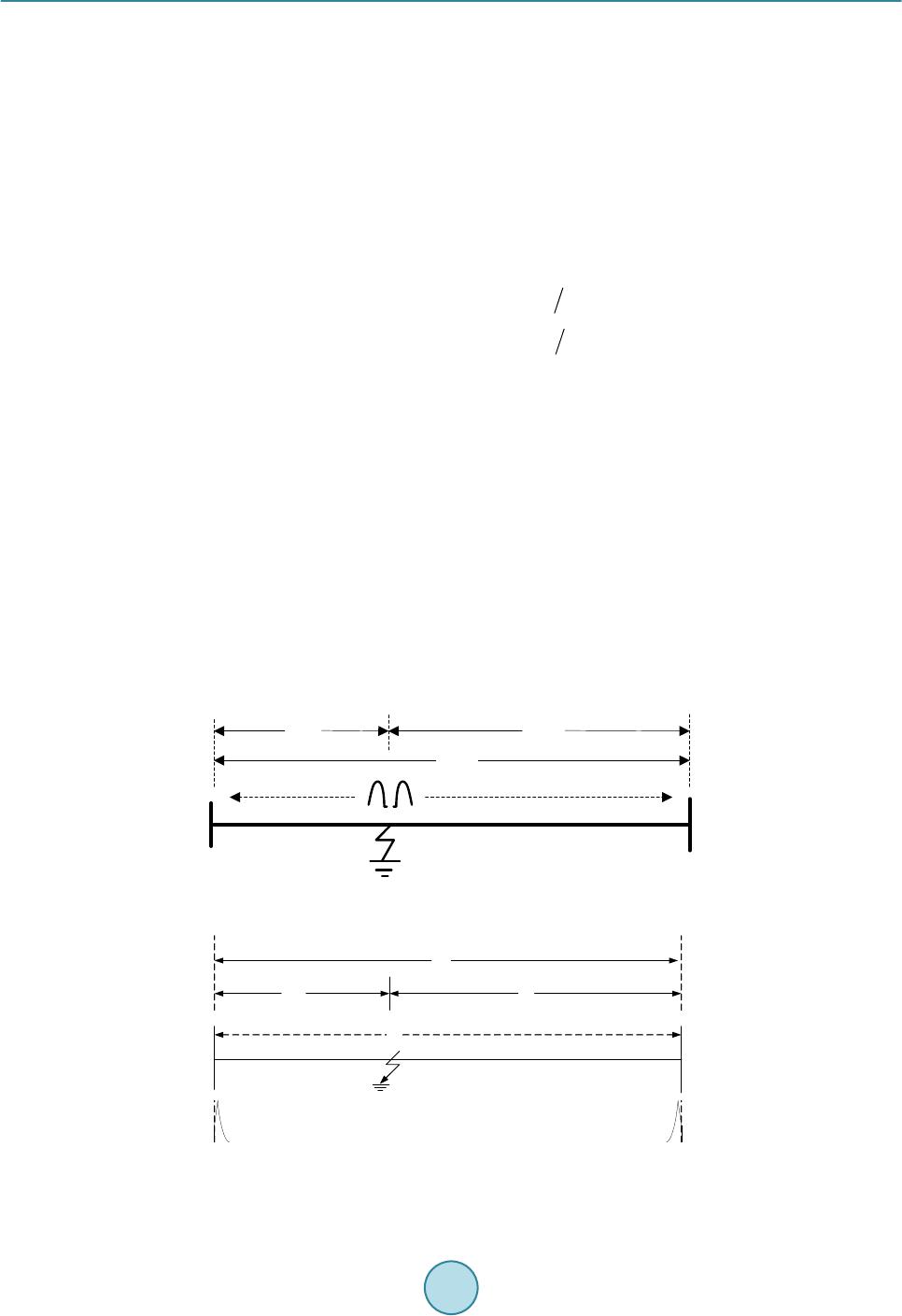 J. Liu et al. Then, the corresponding wave speed of the traveling wave fault is changeable rather than a certain value. At present, in the fa u lt detection of the HVDC system, fixed wave speed is simply selected in fault location [8]. To summarize the relevant literature, the calibration of the traveling wave head and the determination of the wave speed is independent. It will further increases ranging error. In this paper, HHT is applied to traveling wave fault location, and also puts forward an algorithm that the wave head and wave speed are coordinated. Relevant simulations are performed in EMTDC, and the results ve- rify the correctness of this method. 2. Basic Principle of Traveling Wave Fault Location The basic principle of the improved double-terminal traveling wave fault location is shown in Fig ure 1, tm and tn represent the arrival time of traveling wave, L is the length of the line. (1) (2) Equation (1) and Equation (2) show that the accuracy of the double-terminal fault location is mainly affected by the wave speed and the arrival time of the initial wave. The improved double-terminal fault location method is shown in Figure 2, where L is the length of the line, R and I represent the rectifier and t he inverter side of the DC system. and are the distance from the fault point to the rectifier and the inverter side. The fault occurs at , and are the arrival time to both sides. The arrival speed are and , respectively. According to the relation of wave speed, transmission time and fault distance we can get the following equa- tions: (3) (4) (5) The improved double-terminal fault location equation is as follows: Figure 1. D type double-terminal traveling wave principle. Figure 2. Principle of the improved double-terminal fault location method. 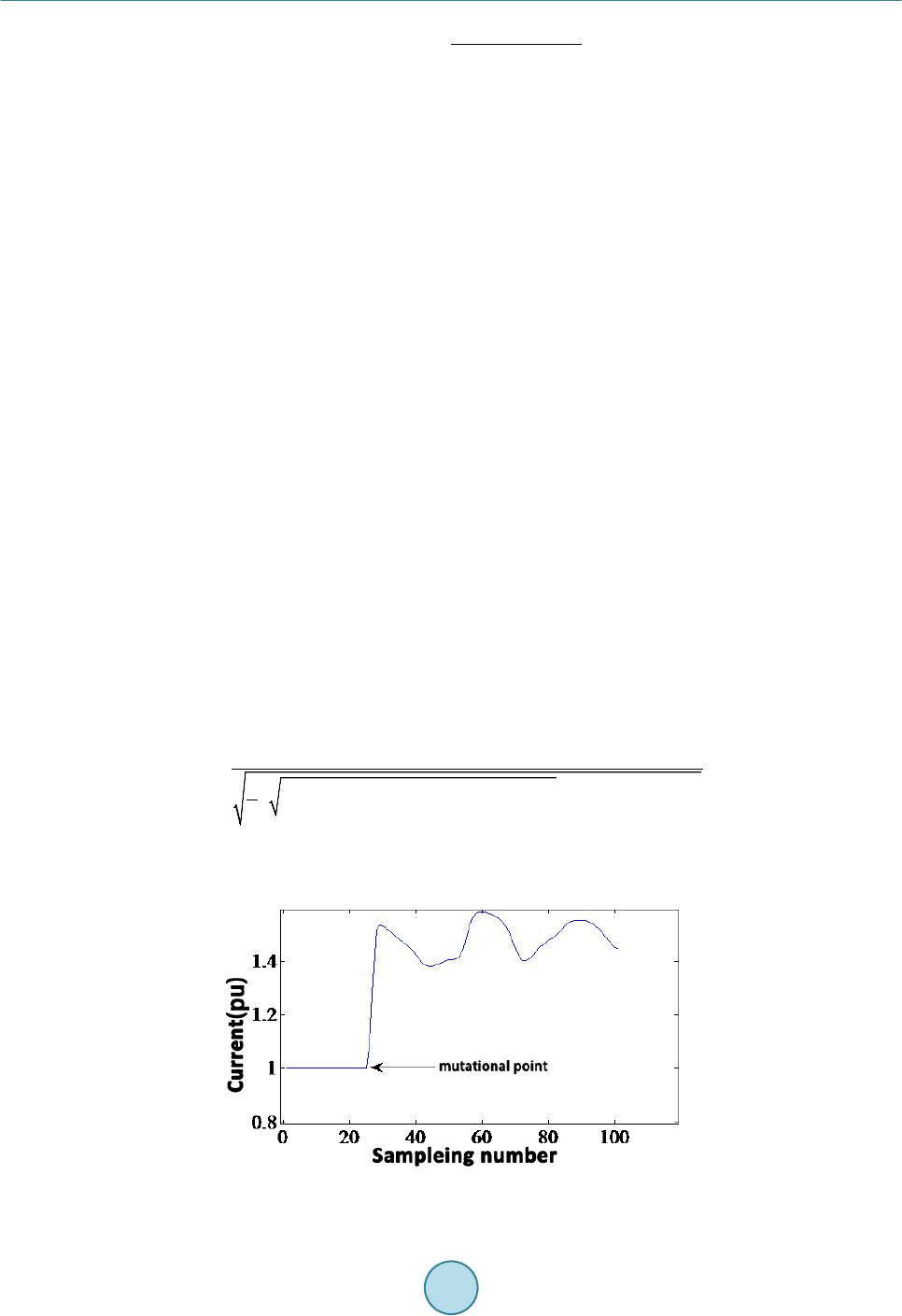 J. Liu et al. (6) 3. Improved Fault Location Algorithm Based on Hilbert-Huang Transform HHT is an effective method in non-stationary signal analysis [9] [10]. It is mainly composed of empirical mode decomposition (EMD) and Hilbert Transform. EMD is based on the local characteristic time scale of signal and decompose the complicated signal into a number of Intrinsic Mode Functions (IMFs). By analyzing, each com- ponent of IMFs involves the local characteristic of the signal. Ensemble Empirical Mode Decomposition (EEMD) is used to resolve problems of mixed mode and false components in the decomposition process of EMD. The white noise is added to the signal so that the signal will have a better decomposition. 3.1. The Arrival Time of Traveling Wave When a fault occurs, the fault point would produce a step wave. The step wave spreads along the line. When a high frequency component arrives at the measuring point firstly, the time can be defined as the arrival time of the frequency components [6]. At the same time, the arrival of the step wave will cause the change of the singu- larity of transient voltage and current of the measuring point [11] [12]. The first instantaneous frequency’s mu- tational point repr esents the arrival time of the fault wave. The HHT extracts IMFs of traveling wave through EMD. The Hilbert Transform is applied to calculate the corresponding instantaneous frequency of the highest frequency component (IMF1). The arrival time of the traveling wave can be detected by the first instantaneous frequency’s mutational point in the time-frequency di- agram of IMF1. When the monopole grounding fault occurs at a distance of 400 km from rectifier side and its transition resis- tance is , the current is shown in Fig ure 3. From Fig ure 3 the singularity time of the current is 2.0014 s, what means that the arrival time of traveling wave is 2.0014 s. The time-frequency diagram of IMF1 is shown in Fig ure 4. From which the first instantaneous frequency’s mutational point is 2.0014 s. That means the HHT can be applied to define the arrival time of the traveling wave. 3.2. The Speed of the Fault Traveling Wave Speed v of a frequency component f is shown in Equation (5), which, according to the literature [13]-[15] is: ( ) ( ) ( ) 22 22 2 000000 000000 1 2 v rgLCLg rCrgLC ω ωω ω = ++− −− (7) where is the angular frequency of the frequency components. , , and are unit length resis- tance, conductance, inductance and capacitance, respectively, they vary with f. Figure 3. current with line faults. 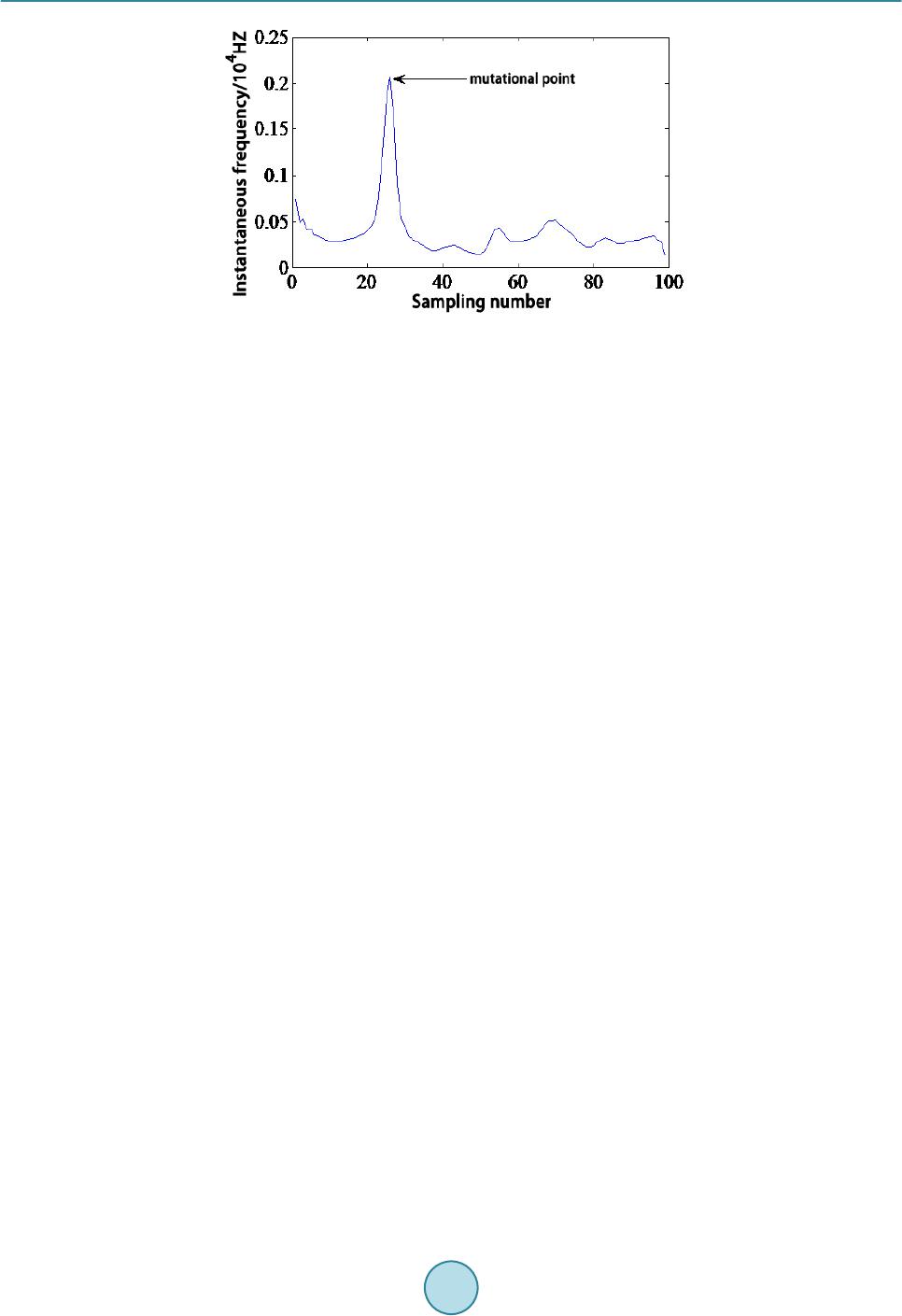 J. Liu et al. Figure 4. Tim e-frequency diagram of IMF1. Each frequency component of the traveling wave has a different speed of propagation, it is unrealistic to ob- tain the exact actual parameters. Therefore, this paper proposes the frequency-wave speed graph according to the parameters of the HVDC line, which is shown in Figure 5. Through which the wave speed is attained. That means the incoordination of the wave speed and the wave head is solved. 3.3. Improved Fault Location Algorithm The improved double-terminal algor ithm is as follows: • When a fault occurs, detect the data of positive and negative DC voltage in both sides. • Make phase-model transformation of the voltage to get the line model data. • EEMD and the Hilbert Transform are done to get the Time-frequency graph. • Use the Time-frequency graph to determine the arrival time of the traveling wave at both sides and the cor- responding instantaneous frequency. • Use the frequenc y-wave speed graph (Figure 5) to get the corresponding line mode speeds . • Calculate the fault distance through Equation (6). 4. Simulation Test 4.1. Simulation System and Its Parameters For the simulations in EMTDC, the network, depicted in Figure 6, corresponds to a typical 500 kV line in a HVDC system. The line length is 1000 km. The fault occurs at 1.5 s. The sampling rate is 1000 kHz. 4.2. The Simulation Results and Analysis 1) Monopole grounding fault The fault occurs at 100 km from the rec ti fier side, and the transition resistance is 0 . Figure 7 shows the frequency-time graph. The arrival time of the initial fault wave to the recti fier side is 1.500336 s, and its corres- ponding transient frequency is 106,111 Hz. Similarly, through Figure 8 the arrival time of the initial fault wave to the inverter side is 1.503027 s and its corresponding transient frequency is 50,086 Hz. The wave speed of the initial fault wave to the rectifier side and the inverter side r espectively are and. Equation (6) is used to calculate the fault point, which is 100.1107 km away from the rectifier side, the absolute error is 0.1107 km, and the relative error is 0.1107%. Monopole grounding fault of different fault distance and different transition resistance, the calculated fault distance are shown in Table 1. Table 1 shows that no matter where the fault occurs, the absolute error is within 1%, which is met with the precision and is less affected by the transition resistance. 2) Inte r-electrode fault If the fault occurs at 100 km away from the rectifier side, and the transition resistance is 0 Ω. Figure 9 shows  J. Liu et al. the frequency-time graph. The arrival time of the initial fault wave to the rectifier side is 1.500326 s, and its corresponding transient frequency is 96,124 Hz. Similarly, through F igure 10 the arrival time of the initial fault wave to the inverter side is 1.503026 s and its corresponding transient frequency is 44,750 Hz. The wave speed to the rectifier side and the inverter side respectively are and . The calcu- lated fault point is 98.7999 km from the rectifier side, the absolute error is 0.2001 km, and the relative error is −1.2001%. Figure 5. Frequen cy-wave speed graph. Filter Filter Filter Filter Rectifier side Inverter side Figure 6. A simplified model of the DC transmission system. Figure 7. Tim e-frequency graph (Rectifier side). 2468 10 12 x 10 4 1 .8 2 2 .2 2 .4 2 .6 2 .8 3 x 10 5 freq u en cy( Hz) wave speed(km/s) frequency-wave characteristics of the line line model zero module 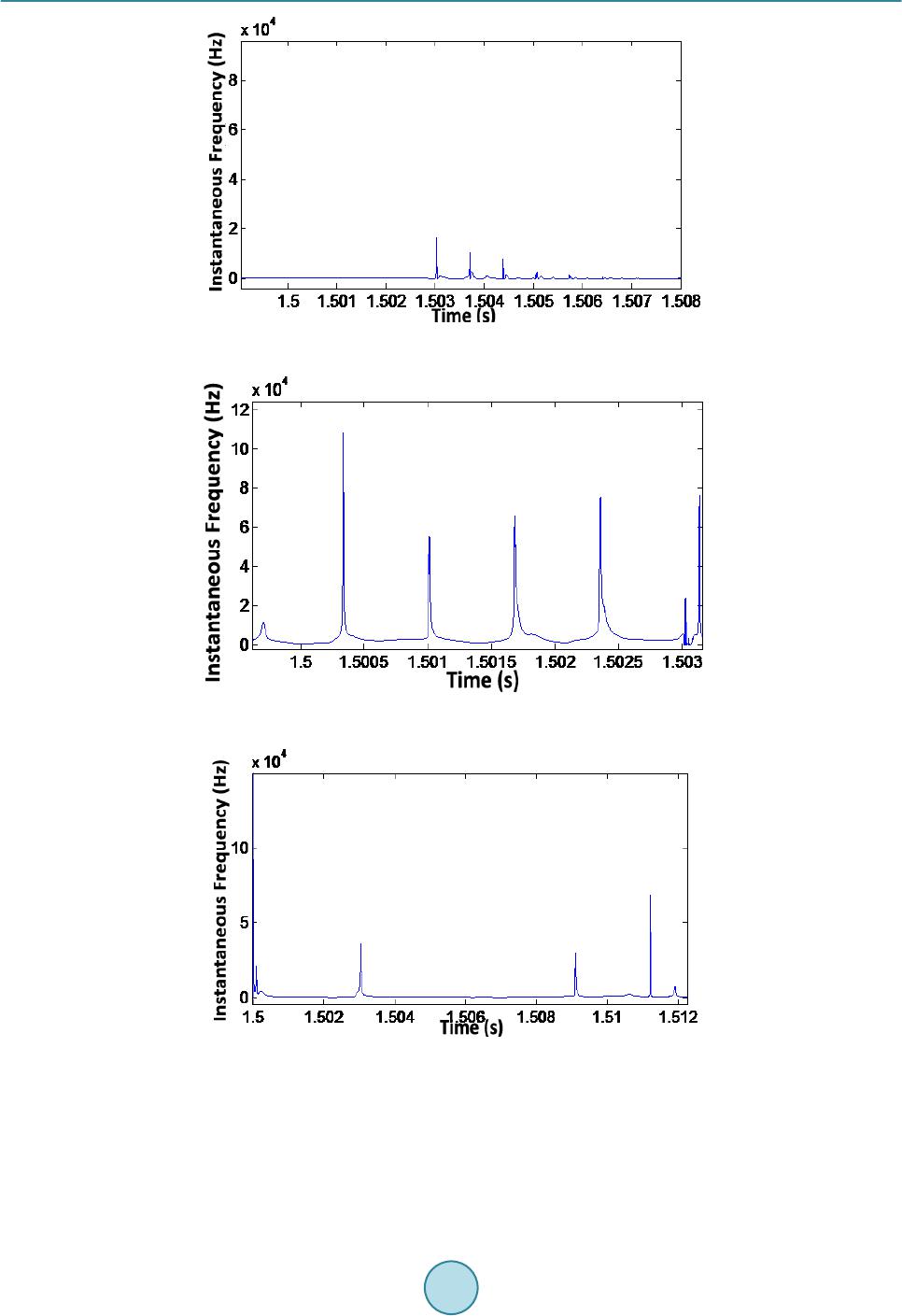 J. Liu et al. Figure 8. Tim e-frequency graph (Inverter side). Figure 9. Tim e-frequency graph (Rectifier side). Figure 10. Time-frequency graph (Inverter side). Interelectrode fault of different fault distance and different transition resistance, the calculated fault distances are shown in Table 2. Through Table 2, the absolute error is basically within 1%, which meets the accuracy requirements. Yet in the same fault distance, compared with the monopole grounding fault the result is reflected by the transition re- sistance much more greatly. The relative error is bigger than the monopole grounding fault error. Thus, fault  J. Liu et al. Table 1. Different fault characteristic (monopolar grounding fault). Fault distance (km) Transition resistance (Ω) Measured fault distance (km) Absolute error (%) Relative error (km) 100 0 100.1107 0.1107 0.1107 100 100.1393 0.1393 0.1393 300 0 300.0214 0.0071 0.0214 100 300.0382 0.0127 0.0382 500 0 500.1009 0.0201 0.1009 100 500.0084 0.0016 0.0084 700 0 699.9853 −0.0021 −0.0147 100 700.0089 0.0012 0.0089 900 0 899.8456 −0.0171 −0.1544 100 899.8456 −0.0171 −0.1544 Table 2. Improved double-terminal algoriTHm (Interelectrode fault). Fault distance (km) Transition resistance (Ω) Measured fault distance (km) Absolute error (%) Relative error (km) 100 0 98.7999 −1.2001 −1.2001 100 100.4450 0.4450 0.4450 300 0 301.9498 0.6499 1.9498 100 301.6695 0.5565 1.6695 500 0 498.6878 −0.2624 −1.3122 100 495.8477 −0.8305 −4.1523 700 0 701.7501 0.2500 1.7501 100 701.6065 0.2295 1.6065 900 0 899.9673 −0.0036 −0.0327 100 900.1278 0.0142 0.1279 typ es have some influence on the fault location result. 5. Conclusion The paper considered fully the dispersion charac ter istic s of the traveling wave, and proposed the improved fault location algorithm. Through the improved HHT, and the initial arrival time of the fault traveling wave, the cor- responding wave speed is determined. It is meaningful to improve the location accuracy of the traveling wave fault location. From the relevant simulations, wherever monopole grounding fault occurs, the ranging relative error is within 1%, and the result is less affected by the transition resistance. Ye t, when interelectrode fault oc- curs, the result is relatively larger. Making the algorithm adapt to different fault occasion will be the next em- phasis for future research. References [1] Wu , L.-Y., He, Z.-Y. and Qian , Q.-Q. (2008 ) A Frequency Domain Approach to Single-Ended Traveling Wave Fault Location . Proceedings of the CSEE , 28 , 98-103. [2] Dong, X.-Z., Ge, Y.-Z. and Xu, B.-Y. (1999) Research of Fault Location Based on Current Traveling Waves. Pro- ceedings of the CSEE, 19, 76-80. [3] Lu , W. (2011) Research of Transient Current Protection Algorithms for HVDC Transmission Lines. Xi’an University  J. Liu et al. of Technology. [4] Ma, C.-R. (2007) Prospect and Development of Transmission Line Fault Location using Traveling Wave. Relay, 35 , 11-15. [5] Deng, B.-F. (2008 ) HVDC Line Protection Summary of Tian-Guang Project. Power System Protection and Control, 36 , 71-74. [6] Tan , J., Huang, Z., Qiu, Y.-F., et al. (2004) Wavelet Transform Based Double Terminal Method of Traveling Wave Fault Location in Double-Circuit Parallel Transmission Line. Automation of Electric Power Systems, 28, 51-55. [7] Huang, Z.-J. and Che n, Y.-P. (2006) Selection of Wavelet Bases for Traveling Wave Fault Location. Automation of Electric Power Systems, 30, 61-64 . [8] Zhong, Y.-M., Qi n, S.-R. and Tan g, B.-P. (2002) Study on a New Transform Method for Vibration Signal. Journal of Vibration Engineering, 15, 233-238. [9] Zhang, Y.-N., Xu, M., Liu , Y.-H. and Cai, Z.-X. (2011) A Novel Travelling Wave Fault Location Algorithm for HVDC Transmission Lines Considering Variation Characteristics of Wave Speed. 35 , 227 -232. [10] Huang, N.E., S hen , Z. and Retal, L.S. (1998) The Empirical Mode Decomposition and the Hilbert Spectrum for Non- linear and Nonstationary Time Series Analysis. Proceedings of the Royal Society London, 454, 909 -995. [11] Zhong, Y.-M. and Huang, H. (2002) Research on the Local -Instantaneous Signal Analysis Theory of the Hilbert-Huang Transform. Chongqing University, 4. [12] Li, T.-Y., Zhao , Y. and Li, N. (2005) Apply Empirical Mode Decomposition Based Hilbert Transform to Power Sys- tem Transient Signal Analysis. Automation of Electric Power Systems, 29, 49-52. [13] Li, A.-M. (2010) A Study on Fault Analysis and Protection of the HVDC Transmission Line. South China University of Technology, Guangzhou. [14] Matick, R.E. (Lu an , Y.M., et al., Translated) (1982) Transmission Lines for Digital and Communication Networks. Science Press, Beijing, 61-65. [15] Zhang, J., Wang, C., Wu, N. and Shu, H.-C. (2005) HVDC Transmission System Fault Identification and Locating Algorithm Using Mathematical Morphology. Yunnan Electric Power, 33, 15-18. [16] Gri v et, P. (Huang, H.-S., et al. , Translated) (19 83 ) The Physical Basis of High Frequency Transmission Lines. Shan g- hai science and Technology Press, Shanghai, 168 -185. [17] Shu, H.-C. (2009) Signal Processing of Power Engineering Application. Science Press, Beijing.
|