 Journal of Power and Energy Engineering, 2015, 3, 63-68 Published Online April 2015 in SciRes. http://www.scirp.org/journal/jpee http://dx.doi.org/10.4236/jpee.2015.34010 How to cite this paper: Tsaplev, V., Konovalov, R. and Abbakumov, K. (2015) Disk Bimorph-Type Piezoelectric Energy Harvester. Journal of Power and Energy Engineering, 3, 63-68. http://dx.doi.org/10.4236/jpee.2015.34010 Disk Bimorph-Type Piezoelectric Energy Harvester V. Tsaplev1,2, R. Konovalov1, K. Abbakumov1 1Department of Electroacoustics and Ultrasonic Engineering, Saint-Petersburg State Electrotechnical University, Saint-Petersburg, Russia 2Department of Physics, North-West Open Technical University, Saint-Petersburg, Russia Email: val ery@co n vergen ce s-fr.ru Received Oc tob er 2014 Abstract The study of the experimental investigation of a disk-type piezoelectric energy harvester pre- sented. The harvester contains disk bimorph piezoceramic element of the umbrella form and con- tains two disk PZT plates. The element is excited at the base point at its center. The element is supplied by a loading ring mass to decrease its resonance frequency. The dependences of the vi- bration displacement along the radii of the bimorph and the ring mass from the frequency of exci- tation are presented and the output voltage frequency response is also presented as well. The idle mode and the load duty are investigated. The value of the internal resistance of the harvester is obtained using the load characteristic. The piezoelectric specific power is estimated exp erimen- tally. Keywords Piezoelectric Energy Harvester, Umbrella Bimorph Plate, Amplitude-Frequency Characteristic, Flexural Vibration, Specific Power, Output Voltage 1. Introduction Design, study and creation of microminiaturize piezoelectric energy harvesters now is a subject of interest of a great number of researches. The well known reason of this interest depends on the possibility of creation of small, independent and practically inexhaustible sources for a great number of different autonomous electronic devices. These sources transform the waste vibration energy, that exists practically everywhere, to the electrical energy. They do not need external energy sources and do not need expenses to periodic recharges of batteries or their chemical treatme nt . One of the most early works on the usage of the energy vibrations for the needs of the power feeding of mi- croelectronic devices [1] substantiates the advantages of the piezoelectric harvesting method compared with electromagnetic or electrostatic. Very detailed reviews [2] [3] show, that the main advantage of the piezoelectric method of harvesting by comparison with other methods of conversion is the greater output power density, and the simplicity of construction. The range of obtained values of voltage is more than obtained with the help of 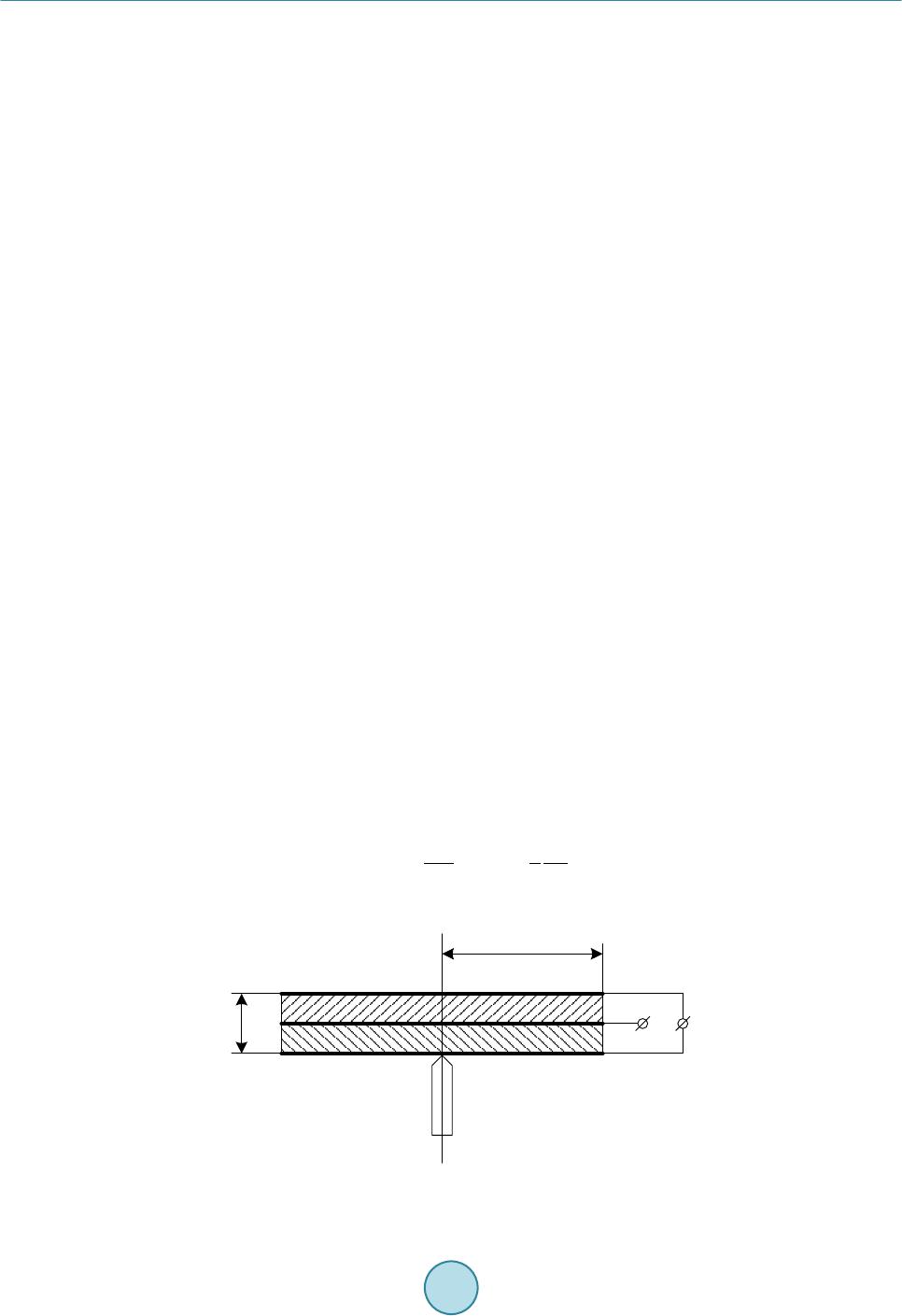 V. Tsaplev et al. other types of harvesters. The main shortcoming of the piezoelectric method of harvesting is the great output re- sistance, but it is easily possible to eliminate this difficulty by proper choice of piezoelements in the harvester and by proper coupling them together in parallel or in series mode of connection. Moreover, this disadvantage one can turn into an advantage-by proper combination of elements and their connection one can obtain any val- ues of output voltage and output impedance desired. Piezoelectric harvesters generate less power density, than solar cell batteries, but our estimations show, that this parameter of piezoharvesters may also be competitive with that of solar ones, if use the nonlinear mode of piezoelements. Therewith, the efficiency of solar cell batteries strongly depends on the solar activity at the place. Various types of piezoelectric harvesters were in detail reviewed in [4]. It was shown, that it is possible to use both longitudinal and transversal modes of oscillations, but mostly piezoelectric harvesters are made in the form of cantilever beam, one end of it being clamped and the other is free, or may be loaded by a passive mass. One or two piezoelectric layers are pasted to the beam thus making a unimorph or bimorph construction. Three or more piezoelectric layers are also possible. The beam is excited at the base point. The passive load mass is used to reduce the main resonance frequency of the beam thus lowering the frequency range of the whole construc- tion. Thus, we can conclude, that the piezoelectric method of energy harvesting provides much more freedom in the choice of specific construction. In this paper we describe disk bimorph-type piezoelectric transducer for energy harvesting. Unlike to the cantilever beam this construction seems to be more rational in relation to the arrangement. 2. Construction Bimorph piezoelement for the piezoelectric energy harvester is shown in diagram form in Figure 1. The theory of a disk bimorph piezoelement, supported at the periphery and vibrating at the bending mode, is described in [5] [6]. Here we consider a bimorph umbrella-type piezoceramic element, free at the periphery and excited at the center, the vibration amplitude being small in comparison with its thickness. The initial equations of piezoeffect are written as following: 11 1231 12 1131 31 3133 , , , EE rr rrz EE rr z z rrz u ssdE u ssdE Dd dE θθ θθ θθ σ θθ σσ σσ σ σε =++ =++ =++ (1) where , -strain tensor components, , -bending stress tensor components, -electric field strength, -electric induction, , -elastic compliance tensor components, electric field strength being constant, -piezoelectric modulus tensor components, -dielectric permittivity tensor components of pie- zoceramics, under constant value of elastic stress. Bending elastic strain tensor components are defined as fol- lowing: 2 2 dd , d d rr z uz u rrr θθ ηη =−=− (2) Figure 1. Bimorph transducer with central excitation.  V. Tsaplev et al. where z-axial coordinate, r-radial coordinate, -angle, -bending deflection. One must mind, that in the ab- sence of volume charges , and without the magnetic field . Then the voltage across the bi- morph plates is ( )( ) 20 02 0 d,0d h zz h UzEz UzEz − >= <=− ∫∫ , (3) And the transducer current , (4) where h-the whole thickness of the plate, a-disk radius, -circular frequency. Equation of motion for bending vibrations under harmonic excitation at the centre of bimorph plate we can write as ( ) 22 2 d dcos dd r t rM MrhF t r r ω ρηω − −= , (5) where and -bending torque intensity per length unit: 22 22 d, d hh tr rr hh Mzz Mzz θθ σσ −− = = ∫∫ , (6) And -piezoceramic density. Boundary conditions at the centre of the disk: (7) But mind, that “pure bimorph” construction is well suitable for usage as the receiving transducer, but is not very suitable for energy harvesting. Mechanical stress in the layers of piezoceramics, adjacent to the neutral plane, is very small, and the electrical energy in these layers is also very small. Such mode of operation is good to receive weak acoustic signals that are subject to subsequent amplification. The weak signal provides low non- linear distortions and clipping the signal. Nonlinear distortions have no importance in the case of energy har- vesting. On the contrary, piezoceramics in nonlinear mode has much greater piezoelectric modulus, than at low levels of excitation. It was shown experimentally [7], that if the level of mechanical stress in piezoceramics is about 60 - 80 МPа, the transverse piezoelectric modulus d31 of the soft piezoceramics (as, for example, PZT-19) has the value about three times as much as the ordinary value (about 300 × 10−12 C/N, instead of specified value 100 × 10−12 К/Н). The electric power density is directly proportional to the second power of piezoelectric mod- ulus, that is why, the usage of the nonlinear vibration mode provides gain in energy by order of magnitude greater than in linear mode. It means, that the transducer must have rather thick base metal plate with two bimorph piesoceramic plates, having oppositely directed polar vectors. If the base is rather thick, the piezoceramics works in the range of sig- nificant mechanical stresses. But in this case the thickness of the whole construction also increases, and the piezoelectric transducer be- comes high-frequency and comes out of the necessary range of vibration frequencies. The main frequency of the umbrella resonance also increases. To reduce this main frequency it was used the metal circumferential passive mass. The whole transducer is shown in Figure 2. The nonlinear elastic properties of PZT-19 piezoceramics are in detail described in [7] [8], and in this paper we do not touch these problems. Here we just concern the study of experimental model at low-level excitation. 2. Experimental Res ults The model of the piezoelectric energy harvester for experimental investigation is shown in Figure 3. The model consists of piezoelectric bimorph element on the bronze base plate pasted into the massive bronze ring. The cross-section of the piezoelement is shown in Figure 3(a) . Bimorph piezoelement consists of two piezoceramic PZT -19 plates, their dimensions are ∅32.0 × 0.2 mm. The piezoelement is pasted into the bronze ring (the in- ternal diameter is 32 mm, the external one is 70 mm, and the thickness is 8 mm). The cylindrical base is pasted 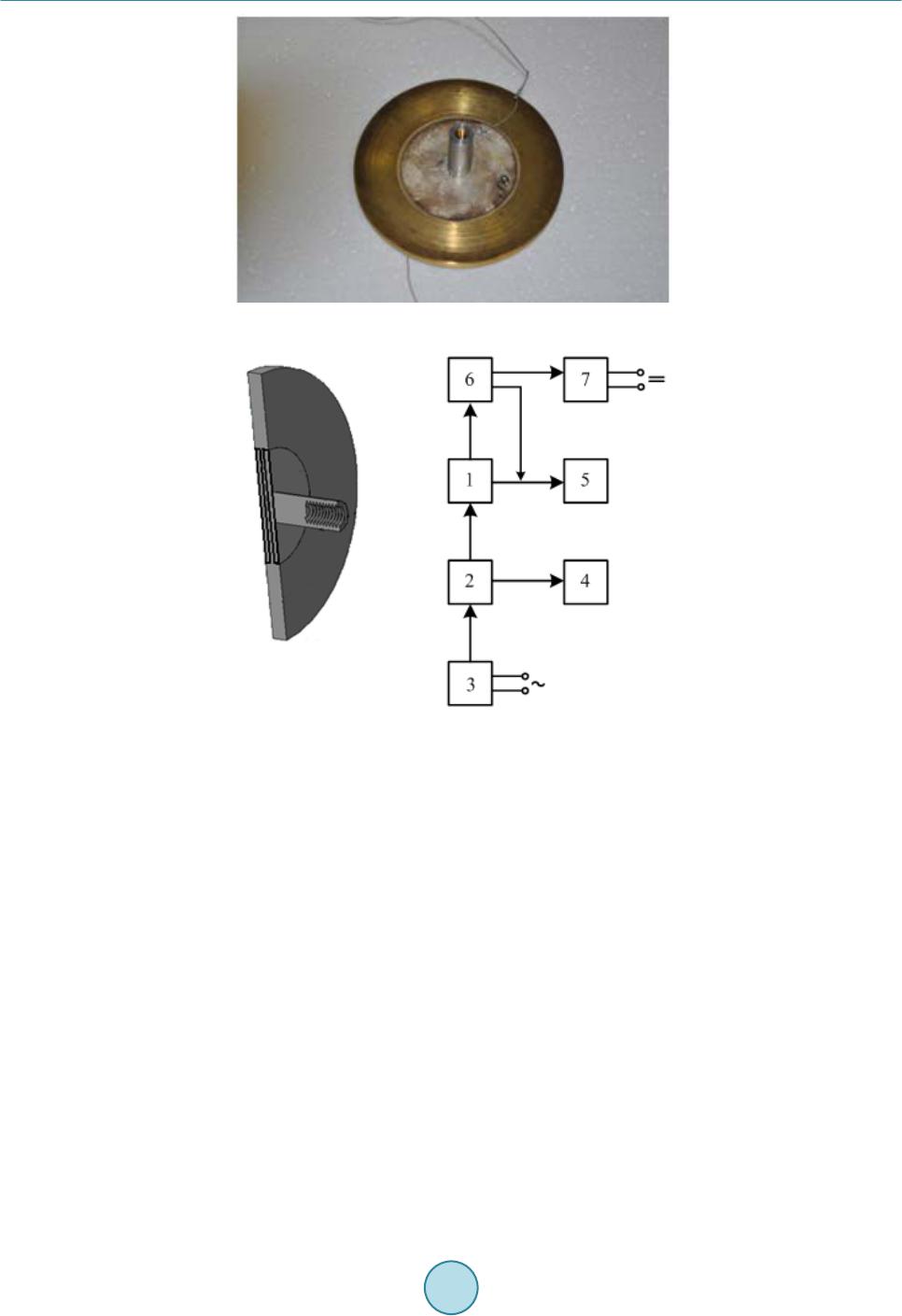 V. Tsaplev et al. Figure 2. Bimorph transducer with passive circular mass. (a) (b) Figure 3. Cross-section of the bimorph transducer and the ex- perimental setup. to the centre, thus making an “umbrella” construction. This base serves to fasten the transducer to the shaker. The piezoceramic plates were pasted to the base bronze plate in such a way, that their polarization vectors looked towards each other. The outside silver electrodes were connected electrically together, as it is showed in Figure 1, and the internal silver surfaces were soldered on to the base bronze plate. The experimental setup is shown in Figure 3(b). The piezoelectric transducer 1 was drived by the electrody- namic shaker 2, that in turn was excited by oscillator 3. The frequency was measured by the frequency meter 4. The output signal was measured by the electronic oscilloscope 5 (LeCroy WaveAce101). The amplitude of the vibrational displacement was measured by small vibration pick-up 6 (KD 91 PCB Piezotronics Inc.) with flat amplitude response from 1 Hz up to 15,000 Hz and 7 is the digital amplifier and registrator. The values of amplitudes of vibration displacements across the surface of piezoelectric transducer were mea- sured at three discrete points: at the centre and at two points −13 and 27 mm away from the centre. The sensor was small enough and its mass did not affect essentially the results of measurements. Figure 4 is the overview of the experimental setup. Figure 5 shows the amplitude-frequency response of the open-circuit, piezoelectric energy harvester. Maxim- al amplitude values of vibration displacements on the surface of transducer versus frequency f are plotted for three points on the surface. Curve 1 is for the point at the centre of the bimorph element, curve 2 corresponds to the point 13 mm away from the centre, and curve 3 is for the point 27 mm from the centre. One can observe that the frequency, corresponding to the maximal amplitude displacement decreases as the point of measurement  V. Tsaplev et al. moves off the centre. This may be explained by the influence of the mass of sensor, though other reasons may be possible as well. Следует отметить, что наблюдается смещение максимумов кривых в сторону более низких частот. This may be a subject of further study. The maximal vibration displacement on the surface of the bimorph plate is at the centre, and minimal at the periphery. Figure 6 shows the amplitude-frequency response of the open-circuit harvester. The maximal value of the 0pen-circuit output voltage was 32 V and was restricted only by possibilities of the shaker. The internal impedance characteristic was measured at the main resonance frequency by output load voltage characterization. It was about 17 kOhm. The output electric power at the matched load was about 15 mWt, and the output power density about 50 mWt/sm3. Figure 4. The overview of the experimental setup. Figure 5. The amplitude-frequency response of the open-circuit transducer. 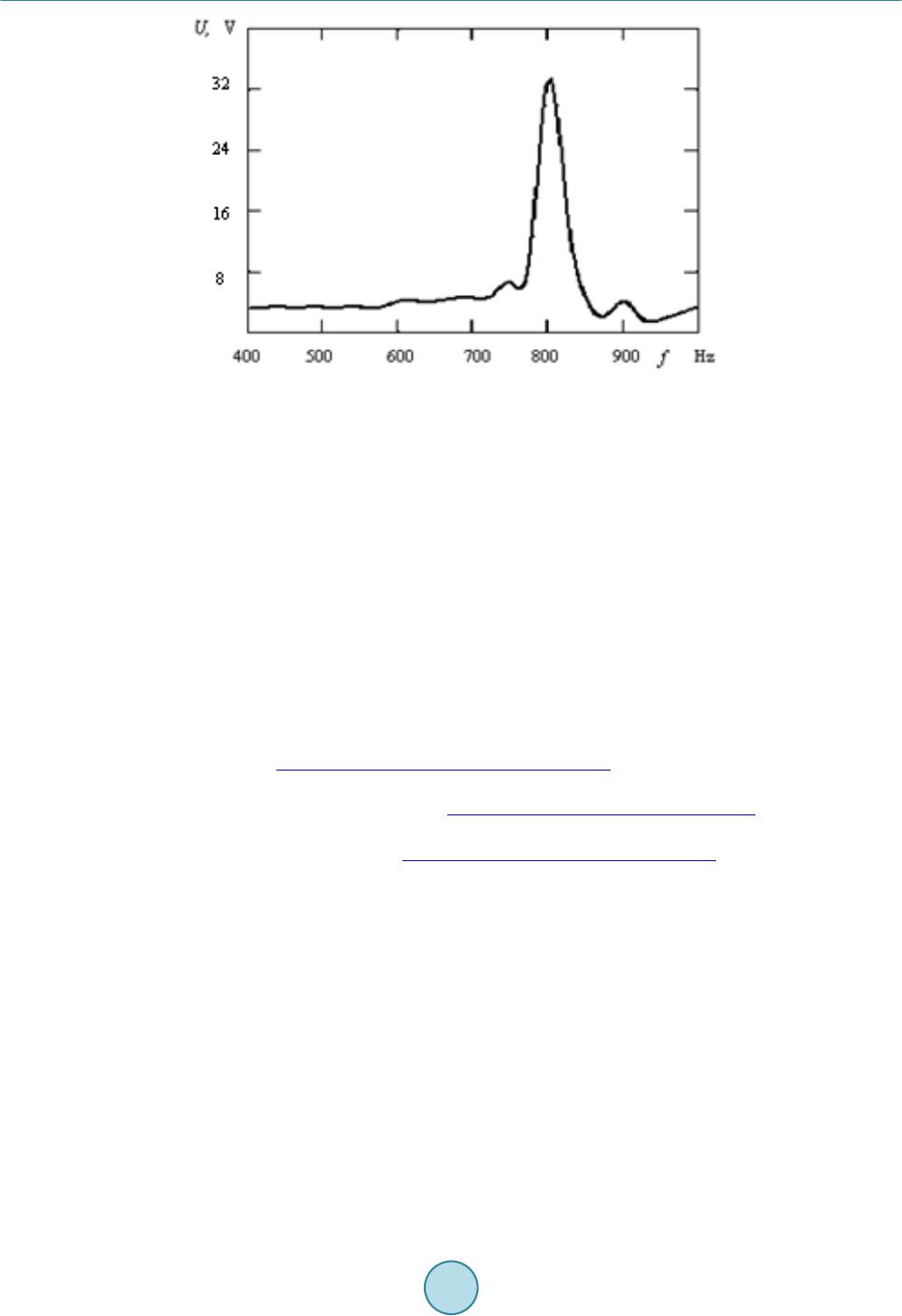 V. Tsaplev et al. Figure 6. The amplitude-frequency response of the open-circuit transducer. 3. Conclusion The results of the experiment show, that the design of this type of piezoelectric harvester provides some advan- tages as compared with cantilever beam-type harvesters. The main advantage is the possibility of increasing the total number of piezoelements, their total volume, and creation of multilayer constructions. This in turn makes possible the usage of nonlinear mode of vibration, thus increasing the output power. Acknowledge ment s This work has been accomplished as a part of the Ministry of Education and Science of the Russian Federation research assignment ‘Realization of scientific research (fundamental studies, applied research and advanced de- velopments)’. Project code: 2548. References [1] Williams, C.B. and Yates, R.B. (1996) Analysis of a Micro-Electric Generator for Microsystems. Sensors and Actua- tors A: Physi cal, 52, 8-11. htt p: //dx.d oi .or g/1 0.10 16/ 0924 -4247(96)80118-X [2] Sodano, H., Park, G. and Inman, D.J. (2004) A Review of Power Harvesting from Vibration Using Piezoelectric Mate- rials. The Shock and Vibration Digest, 36, 197-205. http://dx.doi.org/10.1177/0583102404043275 [3] Anton, S.R. and Sodano, H.A. (2007) A Review of Power Harvesting Using Piezoelectric Materials (2003-2006). Smart materials and Structures, 16, R1-R21. ht tp ://d x.do i .org/ 10. 108 8/09 64 -1726 / 16/ 3/R01 [4] Erturk, A. and Inman, D.J. (2011) Piezoelectric Energy Harvesting. John Wiley & Sons Ltd., New York. [5] Brailov, E.S. and Vassergisser, M.E. (1980) Evaluation of Flexural Bimorph Disk Piezoelement Characteristics. Akus- ticheskij Z hur nal , 26, 590-595. [6] Antonyak, Yu.T. and Vassergiser, M.E. (1982) Calculated Characteristics of Flexural Membrane Type Piezoelectric Transdu cer. Akusticheskij Zhurnal, 28, 294-302. [7] Tsaplev, V.M. (2013) Nonlinear Acoustoelastisity of Piezoceramic Materials: p. I. Physical Acoustics of Piezoceramics. Saint -Petersburg State Electrotechnical University, Saint-Petersbu rg. [8] Tsaplev, V.M. (2003) Nonlinear Properties and Creep in Piezoceramics. No rth-West State Technical University, Saint- Pet ers bur g.
|