Journal of Biosciences and Medicines
Vol.03 No.04(2015), Article ID:55434,10 pages
10.4236/jbm.2015.34002
Ionization Chamber Dosimetry for Conventional and Laser-Driven Clinical Hadron Beams
F. Scarlat1,2, A. Scarisoreanu2, E. Badita2, C. Vancea2, I. Calina2, Fl. Scarlat3, N. Verga4
1Valahia Univesity of Targoviste, Targoviste, Romania
2National Institute for Laser, Plasma and Radiation Physics-INFLPR, Bucharest-Magurele, Romania
3BitSolutions, Bucharest, Romania
4University of Medicine and Pharmacy “Carol Davila”, Bucharest, Romania
Email: scarlat.f@gmail.com


Received January 2015

ABSTRACT
The practice of using the direct ionization radiation (electrons, protons, antiprotons, pions, ions, etc) or of the indirect ionization radiation (photons, neutrons, etc) in economy and social life has led to the introduction of the absorbed dose magnitude (ICRU 1953) defined as the energy absorbed per mass unit of the irradiated substance. This is a fundamental magnitude valid for any type of ionizing radiation, any irradiated material and any radiation energy. In case of clinical hadron beams generated by conventional accelerators or those controlled by lasers, IAEA TRS 398 recommends the absorbed dose to water. This may be determined employing the calorimeter method with water or graphite, chemical method, fluence based measurements as Faraday cups or activation measurements, and the ionization chamber method. In this paper the selected method was the thimble air filled ionization chamber method for determination of absorbed dose to water.
Keywords:
Absorbed Dose to Water, Ionization Chamber, Hadron Therapy, Hadron Dosimetry, Expand Uncertainty

1. Introduction
The ionization method for determining the absorbed dose in air and next in any irradiated substance by means of Bragg-Gray theory, was used by the Institute of Atomic Physics (IFA) in Bucharest located on Magurele Platform, (established in 1956) with the first 30 MeV Betatron Accelerator built and commissioned in 1960 [1].
Methods, techniques and technologies with bremsstrahlung and electron beams developed at the 30 MeV Betatron that have applications in economy and social life, employed the dosimetry with Siemens ionization cham- bers [2]. Such applications were: non-destructive defectoscopy, photonuclear reactions, elemental analysis, therapy with bremsstrahlung radiation of 30 MeV and therapy with electron beams of 25 MeV [3]. The next step was the use of the method with PTW dosimetric apparatus at the 40 MeV Medical Betatron [4].
Moreover, the method was applied in the dosimetric measurements run at other types of electron accelerators built at IFA, IFTAR (established in 1977 but rooted in IFA) and INFLPR ( re-named IFTAR in 1996), such as: the 3 MeV linear accelerator [5], the 8 MeV technologic betatron [6] [7], the 15 MeV industrial betatron [8], the 11.5 MeV microtron [9], the 10 MeV linear accelerator [10] and the 7 MeV defectoscopic linear accelerator [11].
Today, in its infrastructure, INFLPR includes a Secondary Standard Dosimetry Laboratory at High Energies- STARDOOR [12], accredited by Romanian Accreditation Association (RENAR) to perform testing and calibra- tion in beams of photons, electrons and high-energy neutrons in accordance with SR EN ISO/IEC 17025:2005. The dosimetric measurements performed by the laboratory are traceable to the reference standard developed and maintained by PTB.
It is also worth mentioning that an APOLLON laser system of 10 PW (150 J, 15 fs) [13], now under con- struction on Magurele Platform near Bucharest, induced the idea of using it to generate the therapeutic hadrons beams (protons and carbon ions) with energies of 50 to 250 MeV and 100 to 450 MeV/u, respectively. In this way it is possible to skip the stage of conventional accelerators (isochronous cyclotron, synchrocyclotron, synchrotron and linac types) which also include compact accelerators in the design phase (FFAG, DWA and cyclinac) and directly pass to the alternative of using the laser-driven carbon ion/proton therapy beams [14].
In this respect, it is mandatory to extend the functions of STARDOOR Lab for performing clinical testing and calibration in beams of protons and carbon ions. In view of that the material base is ensured by outfitting the platform with a 10 PW laser and the STARDOOR Lab with cylindrical and plane parallel ionization chambers calibrated at PTB.
Taking into account the above and the experience gained in international hadron-based therapy centers with protons and carbon ions, the reference dosimetry techniques for clinical beams of hadrons-calorimetric dosimetry, chemical dosimetry, ionization dosimetry with Faraday cup and ionization chamber dosimetry-this paper presents how to measure the absorbed dose to water in clinical hadron beams employing the ionization chamber dosimetry.
2. Ionization Method and Materials
2.1. Some Requirements for Clinical Hadron Beam
Clinical proton and ion beams are characterized by two very important parameters. The first parameter is the hadron kinetic energy which provides the practical range, the Bragg Peak or Spred Out Bragg-Peak (SOBP) of it, at any depth of a patient tumour ranging between 2.19 cm (50 MeV) and 376 cm (250 MeV) for protons and between 2.59 cm (1200 MeV) and 33.00 cm (5400 MeV) for carbon ions (Figure 1) [14].
Figure 1. Definitions of practical range, Rp and residual range, Rres, and Spred Out Bragg-Peak (SOBP).
The second important parameter of the hadron beam is represented by the beam particle intensity which provides the administration of the required absorbed dose at the level of the tumour located at any depth in the patient. The hadron beam intensity value is about (1 - 5) × 1010 proton/s [15].
A simple scheme for the calculation of the absorbed dose starting either from the tumour (the absorbed dose εT, tumour mass mT and dose in tumour DT) to the laser system, or from the laser system (pulse energy εL, pulse peak P0 and τ0 = τFWHM―the pulse duration) to the tumour, is presented in Figure 2 [16].
The operation condition imposed on the scheme in order to provide the absorbed dose DT in the tumor is
 (1)
(1)
This condition requires that the product between the conversion efficiency η of the laser pulse energy into hadrons kinetic energy and laser pulse energy εL should be greater or equal to the absorbed dose in the tumor εT divided by the product between the laser pulse repetition frequency fR and the irradiation time tT established by the doctor overseeing therapy.
2.2. Ionization Method Principle
The ionization method is used to determine the dosimetric quantities which characterize the direct and indirect ionization radiation.
The basic principle of the ionization method with open ionization chambers (not sealed) and closed (sealed) is known [17]. By irradiating the gas in the sensitive volume V of the ionization chamber with energy fluence Ψ [MeV/cm2] of the radiation beam, one may collect a charge (one sign) q [C] measured in volume V filled with ambient air of mass mair and density ρair = 1293 × 10−3 g/cm3 at STP. Types of cylindrical or plan parallel ioniza- tion chambers may be used for absolute dosimetry.
The associated method device is very simple and has three main components: the ionization chamber, an electrometer and a power supply. The ionization chamber, filled with gas (usually ambient air) is a radiation detector in which ions generated by the interaction of a radiation beam (direct or indirect ionizing radiation), are collected due to the existence of an electric field created between two electrodes, between which a potential difference is established. The electrometer is a device that measures very small values of the electrical currents and charge provided by the ionization chambers. The measuring device is electric-power supplied.
Main dosimetric quantities measured or determined by the ionization method with the associated device, ex- cept the correction factors, are: exposure X only for photon only in air, air kerma Kair (≡Ka) the average amount of energy transferred in a small volume from the indirect ionizing radiation to direct ionizing radiation, the absorbed dose in air Dair (≡Da) and the absorbed dose to water Dw, defined as a mean energy imparted by ionizing radiation to a matter in a finite volume V. The unit of absorbed dose is the gray (1 Gy = 1 J∙kg−1).
These quantities are proportional to the measured electrical charge per mass unit
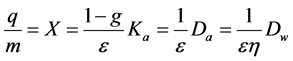 (2)
(2)
where ε is the deposited energy expressed in joule per number of created charge in coulombs (ε ≡ (Wair/e)), sw,air is the stopping power ratio (STPR) of the particle beam for water and air (η ≡ sw,air = (S/ρ)w/(S/ρ)air) and g is the average fraction of energy which transferred to electrons and then lost through radiation processes. The stopping power intervenes in the relation to determine the absorbed dose in any substance different from air as a result of Bragg-Gray theory [17].
Figure 2. Scheme for the absorbed dose calculation.
The current best estimate for the average value of Wair in 60C is 33.97 eV/i.p. or 33.97∙1.602∙10−19 (J/i・p). Taking into account that electrical charge of the ion pair (i∙p.) is of 1.602・10−19 (C/i・p.) it results that for dry air, (Wair/e)e,γ = 33.97 J/C. This value is valid for high energy electron and photon beams [IAEA TRS 398] [18].
Dosimetric quantities (X, Kair, Dair, Dw) determined in the calibration beam of quality Qo (≡60Co γ rays beam) by a reference dosimeter lab have the following calibration factors for the user chambers:
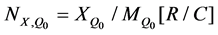 (3)
(3)
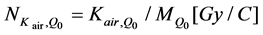 (4)
(4)
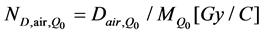 (5)
(5)
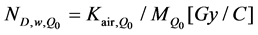 (6)
(6)
In case that one of those dosimetric quantities along with the corresponding calibration factor is determined in the beam of quality Qo, there is the possibility to determine the other three calibration factors using the method of calibration factor conversion given by the relation (2).
For example: knowing the exposure XQo in the calibration beam Qo, and the corresponding calibration factor NX,Qo = XQo/MQo [C/kg], determined by a reference lab for the user ionization chamber, it is possible to determine the calibration factor with the relation (2) of air kerma in air NK,Qo[Gy] = (W/e)airNX,Qo/(1-g), and next ND,air,Qo, Nw,Qo and finally, the absorbed dose to water from a beam of another quality Q, IAEA TRS 277 [19].
The ICRU 59 [20] protocol allows for determinations based on exposure, air kerma, absorbed dose to air and absorbed dose to water calibrations in a 60Co gamma beam [21] [22]. AIEA TRS 398 recommends the determination of the calibration factor for the absorbed dose starting from the absorbed dose to water in the calibration beam Qo.
Yet, in order to compare the medical results of the today and future hadron-based therapy with the results obtained by now with the hadron-based therapy and the conventional therapy and even for verifying the results of the dosimetric measurements, it is necessary that the conversion relations between the calibration factors to exposure: NX,Qo, NK,Qo, ND,air,Qo and Nw,Qo, be defined and measured in the beam of quality Qo in order to determine the corresponding 4 dosimetric quantities [15].
At present there are two protocols of dosimetry which state the formalism and the data referring to the calibration of a ionization chamber in a standard lab for the measurement of the absorbed dose to water under reference conditions in the clinical beam [18].
The first protocol is based on air kerma in air calibration coefficients (formalism NK-ND,w),
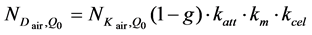 (7)
(7)
where the correction factors (katt. km. kcel) are defined in [18] [19] [23] and the absorbed dose to water based on air kerma is
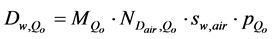 (8)
(8)
With the correction factors 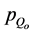 defined in [18].
defined in [18].
The second protocol is based on the absorbed dose to water calibration coefficients (formalismul ND,w). In this case the absorbed dose to water is
 (9)
(9)
From the equality of the relations (8) and (9), it results a second calculation expression for the calibration factor of the absorbed dose to air function of the calibration factor of the absorbed dose to water ND,w,Qo
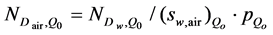 (10)
(10)
The first expression being given by relation (7) function of the calibration factor air kerma in air NK,Qo.
3. Determination of the Absorbed Dose in Proton and Carbon Ion Beams
3.1. Reference Conditions for Dose Determination
The reference conditions for the determination of the absorbed dose in proton and ion beams recommended by AIEA TRS 398 are presented in Table 1.
3.2. Absorbed Dose for Hadrons in Other Quality
The absorbed dose to water in the proton or carbon ion beam of quality Q is given by relation
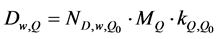 , (11)
, (11)
where MQ is ionization chamber reading in [C] corrected for influence quantities at Q, ND,w,Qo the absorbed dose to water calibration factor of ionization chamber in a beam of quality Qo, and kQ,Qo is the beam quality correction factor of quality Q. Note that relation (11) based on formalism ND,w-IAEA TRS 398 determines the absorbed dose to water Dw,Q (zref) at any user quality Q (protons, carbon ions, electrons, photons, antiprotons, π-mesons etc.).
The distribution of the dose absorbed in depth for clinical protons with energy ranging between 50 MeV and 250 MeV is presented in Figure 3 [24].
The quality factor kQ,Qo can be measured in both qualities Q and Q0 of the beam in a standard laboratory, but, due to the experimental limits, most of the times it is calculated. The values for kQ,Qo were calculated by Formula (12) and are presented in TRS 398, in function of the hadron beam quality parameter Rres. Table 2 is a synthesis of the parameters of the component formula kQQo factor.
The calculation formulae for the factor of quality kQ,Qo is given by the relation
Table 1. Reference conditions for the determination of absorbed dose in proton and ion beams [IAEA TRS 398].
Table 2. Specific factors for Q hadron beams and for the Qo calibration beam.
Figure 3. Relative dose vs. proton depth in water [24].

where sw,air is the water to air mass collision stopping power ratio, (Wair/e)p is the mean energy required to produce an ion pair in dry air and pQ is a correction factor accounting the perturbation by the presence of the ion chamber in the phantom [18] [19].
Equations (11) and (12) may be expressed in the form of the product of three factors [25]:

The first factor represents the corrected reading of the chamber, the second factor represents the factors specific to the calibration beam and the third factor represents the factors specific to the hadron beam.
The ε = (Wair/e) factor. Based on the analysis of all the experimental measurements conducted by now, for protons TRS 398 recommends the value of ε factor of (Wair/e)p = 34.50 J/C and for the carbon ions, the value of (Wair/e)i.c. = 34.23 J/C , for all energies of the protons and carbon ions beams used in therapy.
The stopping power measured in [MeVcm2/g]. TRS 398 recommends that values for the water-to-air mass electronic stopping power ratio in the proton beams, (Sw,air)p be calculated using the quality parameter Rres, in expression

where a = 1.137; b = −4.3・E−05 and c = 1.84・E−03.
At present, TRS 398 recommends for the water-to-air mass electronic stopping power ratio in the carbon ions beams a constant value of the (sw,air)i.c. = 1.13. Calculus performed with SRIM gives the value of (sw,air)i.c. = 1.14.
In this case, the mean ratio of mass electronic stopping powers of the water medium to air, (sw,air)Qo = 1.133 in the Co-60 calibration beam-IAEA TRS 398 recommended value, calculated by Andreo using mono-energetic electron stopping power data tabulated in ICRU Report 37 [26].
Figure 4 presents the distribution of the stopping power for carbon ions in the clinical energy range of 50 MeV/u to 450 MeV/u [27].
Stopping power formulas for heavy charged particles and for electrons and positrons are given in NBSIR 82-2550-A [28] and in ICRU 49 [29].
3.3. Absorbed Dose for Hadrons When kQ,Qo Is Known
Protons. Factor kQ,Qo value for protons are calculated by Equation (4) as a function of the beam quality index
Figure 4. Stopping-power ratios as a function depth in water for carbon ions [27].
Rres defined as (IAEA 2000 TRS-398) Rres = Rp ? z, where Rp is the practical range and z is the depth of measurement. Rres is related to the most probable energy of the highest proton energy peak in the spectrum. The beam quality correction factor for the PTW chambers within the STARDOOR laboratory, calibrated at PTB, are given in Table 6 for protons.
Having the calibration factor for PTW ionization chamber determined by PTB with the values in Table 3 or for other types, as per TRS 398 and Formula (2), the absorbed dose in the proton beam is determined.
Carbon Ions. The values for factor kQ,Qo for carbon ions calculated in case of cylindrical and plane-parallel chambers of Markus type within STARDOOR lab, are presented in Table 4.
3.4. The Absorbed Dose for Hadrons When kQ,Qo Is Not Known
Protons. In case of proton and carbon ion beams, for the ratio of stopping power water to air, TRS 398 recommends the value of (sw,air)Qo = 1.13 in 60Co gamma radiation according ratios of stopping powers water/air for heavy ions calculated using the computer codes developed by Salamon, Hiraoka and Bichsel. Data for protons and He are from ICRU-49.
To calculate the values of factor kQ,Qo, from the denominator of its expression, all the three are known: (sw,air) Qo = 1.133, (Wair/e)Qo = 33.97 J/C and the third one is in Table 5 (TRS 398). The table presents only the data for the ionization chambers within the STARDOOR lab. For the parameters at factor kQ,Qo expression denominator, the values recommended in TRS398 are selected, namely: (Wair/e)Qp = 34.23 J/C, factor pQ ≈ 1 and factor (sw,air)Qp shall be calculated in function of the hadron kinetic energy.
So, the factors related to the qualities of Co-60 calibration beam are data calculated and presented in TRS 398.
Carbon Ions. Knowing the calibration factor of the ionization chamber in 60Co beam and the other factors which characterize the calibration beam, the quality parameters of the carbon ion beam need to be determined. For carbon ion, TRS 398 recommends the following values: (Wair/e)c.i. = 34.50 J/C, pQ,c.i. = 1 and (sw,air)Qp is calculated in function of the carbon ion kinetic energy.
4. Uncertainties
IAEA TRS 398 recommends for calibration beam specific factors Qo (≡Co-60) the following uncertainty (U) values for sw,air in Co-60 beam:
-STPR: (sw,air)Qo = 1.133% ± 0.1%, for dry air and humid;
-the mean energy expanded in air per ion pair formed: (Wair/e)Qo = 33.97 J/C ± 0.2%;
-pQo the calculus method is given in [18].
Table 3. Calculated values of kQ,Qo for proton beams [IAEA TRS 398].
Table 4. Calculated values for kQ,Qo for heavy ion beams.
Table 5. Values for the factors p and sw,airpQo in 60C gamma radiation [IAEA TRS 398].
Regarding proton beams, IAEA TRS 398 recommends the following values:
-(sw.air)p are calculated as a function of the energy and are presented in 2.4 Paragraph;
-(Wair/e)p = 34.23 J/C ± 1.5%, (Wair/e)p = 34.8 J/C ± 0.7% for dry air and humid air, respectively. In the case of proton beam ICRU 59 recommends (Wair/e)p = 34.80 J/C ± 0.7%.
-pQ ≈1 for protons and carbon ions.
Estimated relative uncertainty for proton beam are presented in Table 6 [30] [31].
In terms of heavy ion beam sIAEA TRS 398 recommends the following values:
-(sw,air)c.i. = 1.13% ± 2% [2];
-(Wair/e)c.i. (weighted median) = 34.5 J/C ± 1.5%;
-p,c.i. = 1.0% ± 1% [2] [10];
Estimated relative uncertainty for carbon ion beams are presented in Table 7 [31].
Table 6. Estimated relative uncertainties (in %) for the quality factors for proton beams [IAEA TRS 398].
Table 7. Estimate relative uncertainties (in %) for the quality factors for carbon ion beams [IAEA TRS 398].
5. Conclusions
The purpose of this paper is to offer a synthesis of all the data required to determine the absorbed dose in water in proton and carbon ion beams, also satisfying the recommendations in TRS 398.
These data allow the outfitting of STARDOOR Lab with the dosimetric equipment required to undergo measurements in proton and heavy ion beams and the finalization of some cross-interpretations with other labs and centers of clinic hadron-based therapy abroad.
These preliminary data may be used to elaborate and implement a technical procedure for the determination of the absorbed dose in hadron beams for an operation point of a conventional acceleration system or an operational point of a laser system.
Moreover, these exploratory studies are necessary and useful for establishing some methods to generate clinical hadron beams (protons and carbon ions for which a rich experience already exists in Europe and worldwide) by means of the 10 PW laser beam that is to be finalized on the Magurele Platform-Bucharest (Romania).
Cite this paper
F. Scarlat,A. Scarisoreanu,E. Badita,C. Vancea,I. I. Calina,Fl. Scarlat,N. Verga, (2015) Ionization Chamber Dosimetry for Conventional and Laser-Driven Clinical Hadron Beams. Journal of Biosciences and Medicines,03,8-17. doi: 10.4236/jbm.2015.34002
References
- 1. Ciorascu, F., et al. (1962) Some Problems of the Commissioning and the Adjusting of the Betatron from the Institute of Atomic Physics. St. Cerc. Fiz., 15, 11, 105.
- 2. Scarlat, F. (1971) Adaptation of the 30 MeV IAP Betatron for Medical Therapy. The 5th International Betatron Symposium, Bucharest-Magurele, Romania, 18-23 October 1971.
- 3. Birzu, I., Grigorescu, St. and Scarlat, F. (1973) Therapeutic and Dosimetric Aspects in the Treatment of Malignant Tumours with a 30 MeV Betatron. The International Conference on Photonuclear Reactions and Applications, Asilomar Livermore, 26-30 March 1973.
- 4. Scarlat, F. (1992) A 40 MeV Medical Betatron. Rev. Roum. Phys.Tome, 37, 615-619.
- 5. Baltateanu, N., et al. (1969) L’accelerateur lineaire a’electrons de 3 MeV. preprint IFA, AL-1, 3-16.
- 6. Haltrich, S. and Scarlat, F. (1967) Parametrii betatronului IFA de 8 MeV. Raport intern IFA, MB-178, 10 Decembrie 1967.
- 7. Haltrich, S., Ivanovici, M., Iliescu, C., Panaitescu, I., Mohor, I. and Scarlat, F. (1970) Ein 8 MeV Betatron Mit Verbesserten Magnetkreis. Kernenergie, Band 13, H.1, S.16-24.
- 8. Baciu, G., Panaitescu, I., Mohor, I., Scarlat, F. and Andreescu, M. (1971) Romanian Industrial Betatron BETI for Non-destructive Testing. The 5th International Betatron Symposium, Bucharest-Magurele, 18-23 October 1971.
- 9. Axinescu, S., et al. (1982) The 17-Orbit Microtron of the Institute of Atomic Physics. All Union Symposium on microtrons and Their Applications, Dubna, U.S.S.R.
- 10. Minea, R., et al. (2004) Accelerators Use for Irradiation Offers Medicinal Herbs. Proc. of EPAC, Lucerne, 2004, 2371-2373.
- 11. Martin, D., et al. (2006) Waste Treatment by Microwave and Electron Beam Irradiation. Proc. of the Environmental Physics Conference, Alexandria, 18-22 February 2006, 91-100.
- 12. Scarlat, F., Scarisoreanu, A., Minea, R., Badita, E., Sima, E., Dumitrascu, M., Stancu, E. and Vancea, C. (2013) Secondary Standard Dosimetry Laboratory at INFLPR. Optoelectronics and Advanced Materials—Rapid Communications, Vol.7, 618-624.
- 13. Zamfir, N.V. (2012) Extreme Light Infrastructure—Nuclear Physics ELI-NP. Experimental Programme Workshop at ELI-NP, Bucharest, 3-5 October 2012.
- 14. Scarlat, F., Verga, N., Scarisoreanu, A., Badita, E., Dumitrascu, M., Stancu, E., Vancea, C. and Scarlat, Fl. (2013) Absorbed Dose Determination in Conventional and Laser-Driven Hadron Clinical Beams. Journal of Intense Pulsed Lasers and Applications in Advances Physics, 3, 5-25.
- 15. Bulanov, S.V. and Khoroshkov, V.S. (2002) Feasibility of Using Laser Ion Accelerators in Proton Therapy. Plasma Physics Reports, 28, 453-456. http://dx.doi.org/10.1134/1.1478534
- 16. Scarlat, F., Scarisoreanu, A., Verga, N., Scarlat, Fl. and Vancea, C. (2014) Evaluation of Physical Parameters for Laser-Driven Clinical Hadron Beams. Journal of Intense pulsed Lasers and Applications in Advances Physics, 4, 55-64.
- 17. ICRU Report 21 (1974) Radiation Dosimetry: Electrons with Initial Energies between 1 and 50 MeV. Quantities and Units. International Commission on Radiation Units and Measurements, Washington D.C.
- 18. IAEA TRS 398. Absorbed Dose Determination in External Beam Radiotherapy. An International Code of Practice for Dosimetry Based on Standards of Absorbed Dose to Water. Tehnical Report no 398.
- 19. IAEA TRS 277. Absorbed Dose Determination in Photon and Electron Beams. An international Code of Practice. Tehnical Report of Series no. 277, Vienna, 1997.
- 20. ICRU Report 59 (1998) Clinical Proton Dosimetry—Part I: Beam Production, Beam Delivery and Measurement of Absorbed Dose, International Commission on Radiation Units and Measurements, Bethesda, Maryland, USA.
- 21. Hartmann, G.H., Jakel, O., Heeg, P., Karger, C.P. and Kriesβbach, A. (1999) Determination of Water Absorbed Dose in a Carbon Ion Beam Using Thimble Ionization Chambers. Phys. Med. Biol., 444.
- 22. Vatnitsky, S., et al. (1999) Proton Dosimetry Intercomparation Based on the ICRU Report 59 Protocol. Rad and Oncol., 51, 273-279. http://dx.doi.org/10.1016/S0167-8140(99)00060-2
- 23. IAEA TRS 381. The Use Plan Parallel Ionization Chambers in High Energy Electron and Photon Beams. An International Code of Practice for Dosimetry. Tehnical Report Series no. 381, Vienna, 1995.
- 24. The Normalized (at Peak) Bragg Curves for Various Proton Incident Energies in Water Phantom: A Simulation with GEANT4 Monte Carlo Code, Abstract ID: 8159. http://www.aapm.org/meetings/amos2/pdf/34-8159-78594-298.pdf
- 25. Karger, C.P., Jakel, O., Palmans, H. and Kanal, T. (2010) Dosimetry for Ion Beam Radiotherapy. Phys. Med. Biol., R193-R234. http://dx.doi.org/10.1088/0031-9155/55/21/R01
- 26. ICRU Report 37 (1984) Stopping Powers for Electrons and Po-sitrons. International Commission on Radiation Units and Measurements, Bethesda, MD, USA.
- 27. Geithner, O., Andreo, P., Sobolevsky, N., Hartman, G. and Jakel, O. (2006) Calculating of Stopping Power Ratios for Carbon Ions Dosimetry. Phys. Med. Biol., 51, 2279-2292. http://dx.doi.org/10.1088/0031-9155/51/9/012
- 28. Berger, M.J. and Seltzer, S.M. (1983) Stopping Powers and Ranges of Electrons and Positrons, National Bureau of Standards NBSIR 82-2550-A, Washington D.C.
- 29. ICRU Report 49 (1993) Stopping Powers and Ranges for Protons and Alpha Par-ticles, International Commission on Radiation Units and Measurements, Bethesda, Maryland, USA.
- 30. IAEA TEDOC 1455. Implementation of the International Code of Practice on Dosimetry in Radiotherapy (TRS 398). Review and Testing. International Atomic Energy Agency, Vienna, 2005.
- 31. IAEA TEDOC 1585. Measurements Uncertanity. A Practical Guide for Secondary Standard Dosimetry Laboratories. Vienna, 2008.






