 Int. J. Communications, Network and System Sciences, 2015, 8, 43-49 Published Online April 2015 in SciRes. http://www.scirp.org/journal/ijcns http://dx.doi.org/10.4236/ijcns.2015.84005 How to cite this paper: Tran, Q.T., Ma, Z.H., Li, H.C., Hao, L. and Trinh, Q.K. (2015) A Multiplicative Seasonal ARIMA/GARCH Model in EVN Traffic Prediction. I nt. J. Communications, Network and System Sciences, 8, 43-49. http://dx.doi.org/10.4236/ijcns.2015.84005 A Multiplicative Seasonal ARIMA/GARCH Model in EVN Traffic Prediction Quang Thanh Tran1, Zhihua Ma2, Hengchao Li1, Li Hao1, Quang Khai Trinh3 1Sichuan Provincial Key Laboratory of Information Coding and Transmission, Southwest Jiaotong University, Chengdu, China 2Beijing Branch of China United Network Communications Co. Ltd., Beijing, China 3Telecommunication Department, University of Transport and Communications, Hanoi, Vietnam Email: thanhktvt@gmail.com Received March 2015 Abstract This paper highlights the statistical procedure used in developing models that have the ability of capturing and forecasting the traffic of mobile communication network operating in Vietnam. To build such models, we follow Box-Jenkins method to construct a multiplicative seasonal ARIMA model to represent the mean component using the past values of traffic, then incorporate a GARCH model to represent its volatility. The traffic is collected from EVN Telecom mobile communication network. Diagnostic tests and examination of forecast accuracy measures indicate that the multip- licative seasonal ARIMA/GARCH model, i.e. ARIMA (1, 0, 1) × (0, 1, 1)24/GARCH (1, 1) shows a good estimation when dealing with volatility clustering in the data series. This model can be considered to be a flexible model to capture well the characteristics of EVN traffic series and give reasonable forecasting results. Moreover, in such situations that the volatility is not necessary to be taken into account, i.e. short-term prediction, the multiplicative seasonal ARIMA/GARCH model still acts well with the GARCH parameters adjusted to GARCH (0, 0). Keywords Traffic Prediction, ARIMA, GARCH, Multiplicative Seasonal ARIMA/GARCH, EViews 1. Introduction Traffic prediction is a key factor for a better network management which is now very important due to the ex- plosive development of mobile communications and internet, especially in Vietnam, where there is a violent competition between so many service providers. Statistical procedure has been used in developing forecasting models that have been applied to many different areas such as seasonal ARIMA in wireless traffic modeling and prediction [1]-[3], or ARCH in load forecasting [4]. Those analyses present many successful applications of ARIMA in forecasting time series data. However, ARIMA can only help presenting the conditional mean of the series. With the implicit assumption of homoske- dasticity, GARCH is absolutely efficient in investigating the volatility characteristics of time series. Therefore, the combination of ARIMA and GARCH is a good choice to give a better result in capturing and forecasting 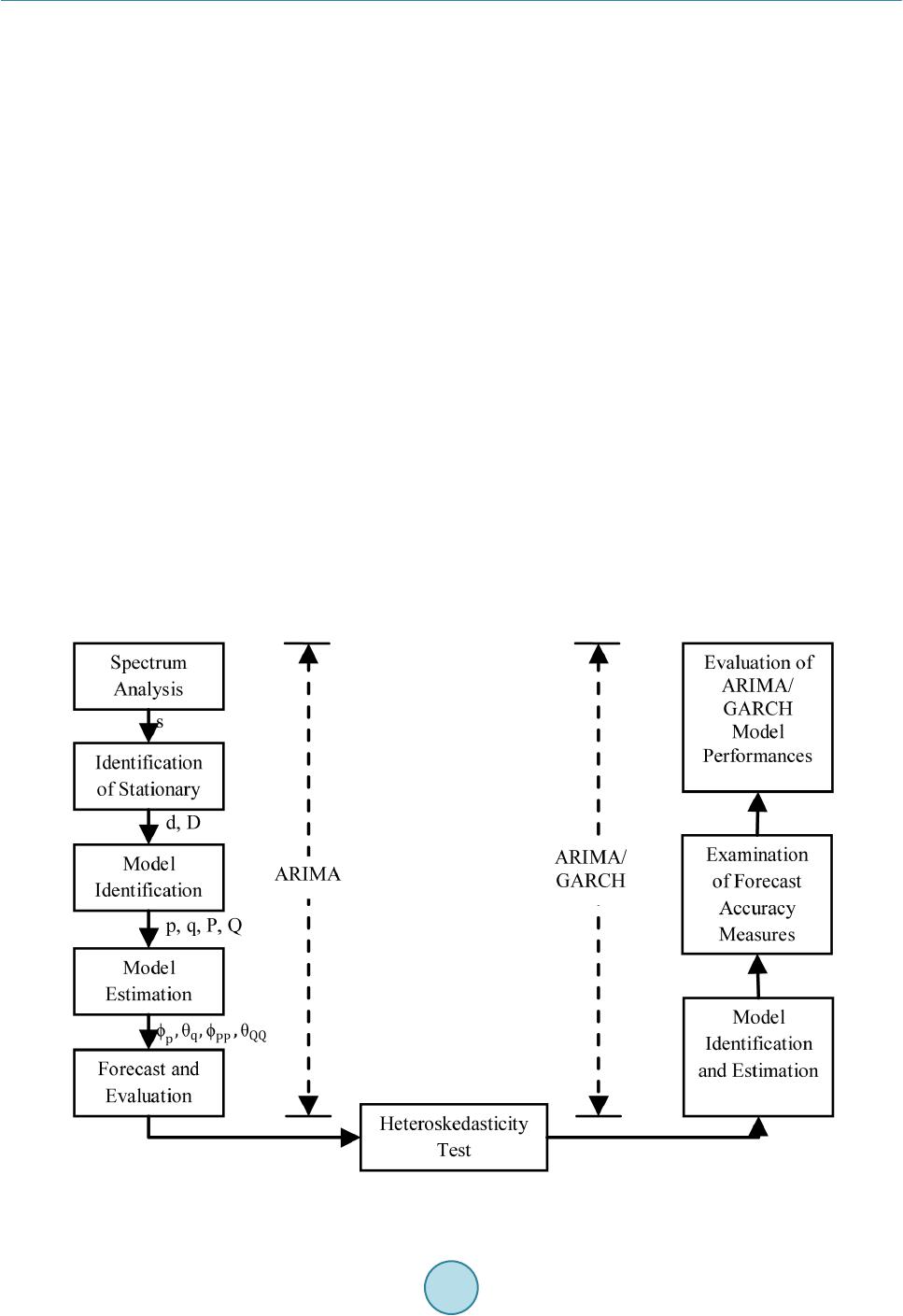 Q. T. Tran et al. time series such as wireless traffic data [5]-[7], crude oil prices data [8], inflation data [9], or internet traffic [10]. In this paper, the combination of ARIMA and GARCH is applied to mobile traffic in the condition of Viet- nam, which has never been discussed before. A multiplicative seasonal ARIMA/GARCH model is built to fit and forecast EVN traffic. The evaluation of information criterion and forecast performance is made. The paper is organized as follows: Section 2 proposes to use multiplicative seasonal ARIMA/GARCH model to fit and forecast EVN traffic. Section 3 presents the experiment results and discussions. Finally, the conclusions are given in Section 4. 2. Propose to Build a Multiplicative Seasonal ARIMA/GARCH Model The detail explanations of a multiplicative seasonal ARIMA model and a GARCH model can be found in refer- ences [1] [9] and [11]-[14], respectively. Below is the briefly description of a multiplicative seasonal ARIMA model which is derived from [1]: ( ) ( ) ( ) ( ) s dDs pPst qQt B BXB Ba φθ Φ∇∇ =Θ (1) Or (2) where, ( ) () ( ) ( ) 11ss tpPq Qt WBB B Ba φθ −− =ΦΘ (3) To build a multiplicative seasonal ARIMA/GARCH model, we first construct a multiplicative seasonal ARIMA to present the mean component using the past values of the EVN traffic. We then incorporate a GARCH model to represent its volatility. The whole progress can be described in the flowchart in Figure 1 be- low. The progress in the flowchart can be expressed step by step as follow: Figure 1. Flowchart of building ARIMA/GARCH process.  Q. T. Tran et al. Step 1: Using spectrum analysis to determine the period s of the traffic trace This step is very important to give a consideration to a seasonal ARIMA model. If s is found, then we can make a decision of a multiplicative seasonal ARIMA which is in the form of . Step 2: Identification of stationary, determine d and D The second step is also very important in fitting an ARIMA model. It is the determination of the order of dif- ferencing needed to make the series stationary. Step 3: Model identification, determining all the orders Propose to begin with candidate parameter sets that have small , values such as 0, 1, or 2 but where p, P and q, Q should not be 0 simultaneously in one set. Then, we can select the best , combination according to the known model identification such as AIC (Akaike Information Criterion) and BIC (Bayesian Information Criterion) [15]. Step 4: Model estimation Estimating all the parameters using approximate maximum likelihood parameter estimation methods, so that we obtain: 12121 212 , , ,,, ,,,,, ,,, ,, pqP PPPQ QQQ φφφθθθφ φφθθθ Step 5: Forecast and evaluation We use the fitted multiplicative seasonal ARIMA models obtained from (3) to forecast the series. Step 6: Heteroskedasticity test The existence of heteroscedasticity in hourly EVN traffic series must be examined before starting to estimate the GARCH model. Step 7: Model identification and estimation for multiplicative seasonal ARIMA/GARCH model We now verify the adequacy of AR and MA terms of the mean equation by implementing the correlogram Q- test, Jarque Bera test and ARCH test on the stationary series achieved from step 2. The result of no serial correlation under the correlogram Q-test will indicate that we can proceed with the es- timation of the conditional variance for the errors using GARCH. We limit the order of to 4, that is we use different orders of p, q = 0, 1, 2, 3 and 4, since GARCH is used for short-term forecasting. Incor- porating the stationary series achieved from step 2 and the mean equation with AR and MA terms achieved from step 3, we estimate a GARCH model by finding a significant order combination under a specific error distribu- tion (p-values should all be less than 0.10 level of significance and coefficient of the variance equation should all be positive). Step 8: Examination of forecast accuracy measures Static forecasting on the model is performed to show measures of forecast accuracy over the estimation period. The model with the smallest measure of forecast error will be chosen as the one with the most accurate fit of the time series model. Then, some more tests will be performed, such as correlogram of standardized residuals squared which consists of autocorrelation and partial auto-correlation, test for presenting of conditional hetero- scedasticity in the data with ARCH-LM test on the residuals, standardized residuals. Step 9: Evaluation of multiplicative seasonal ARIMA/GARCH model performances The final step is to evaluate the forecast performances by our achieved multiplicative seasonal ARIMA/ GARCH model. The evaluation includes the information criterion, i.e. AIC and SIC values in the estimation stage, and forecast performances in the forecasting stage. 3. Experimental Results and Discussions Through spectrum analysis, we can figure out the periodicity of 24 hours or one day and we can say that s = 24 for this traffic. Then, the processes on the correlogram of EVN traffic stream show that the series needs to take the logarithm transformation (EVNLOG) and the 24-period seasonal difference (EVNLOGd0D1) to become variance stationary. Refer to the equation described in (2) we have: (4) where is our series EVN, and is EVNLOGd0D1. In the next step, the estimation performed by EViews shows that the chosen model should have AR (1), MA (1) and SMA (24) components can be expressed as: ARIMA (1, 0, 1) × (0, 1, 1)24 which is implemented on the  Q. T. Tran et al. logarithm form of the original series. Also, the coefficients are: ( )( )() EVNLOGD0D1 0AR10.636844024029,MA 10.316609103164,SMA240.941553237619=+= ==− The obtained fitted multiplicative seasonal ARIMA model can be expressed detail as: ( ) () () () () () 1 24 1 2411 1ln 11 tt B XBBa φθ −∇= −−Θ (5) ( ) ( ) ( ) 1 124 241241111 lnln1 t ttt X XBaa φθ −− ⇔∇− ∇=−Θ− (6) ( ) ( )( ) 124 24 2411251111 11 lnln ln ttt tttt XXXaaBaBa φ θθ −− −− ⇔∇−−=−−Θ+ Θ (7) () ()( )() 241125111241 1125 ln lnlnln ttttttttt t XXXXaaaaa a φ θθ −− −−−−− ⇔−−−=−−Θ−+ Θ− (8) ()( ) 112412511111 2411 25 lnlnlnln11 t ttttttt X XXXaaaa φφ θθ −− −−−− ⇔=+−+−Θ−−Θ+Θ+ Θ (9) where, , , . 1122432511224325 ˆˆˆˆ ˆˆ ˆˆˆˆˆ ˆˆ ln lnlnln tttt ttt XXXX aa a βββθθ θ −−− −−− ⇒=+−− ++ (10) where, , is actual values and is forecast values. The forecast of EVN traffic stream using multiplicative seasonal ARIMA (1, 0, 1) × (0, 1, 1)24 model is now conducted. EViews software provides the one-step ahead static forecasts which are more accurate than the dy- namic forecasts. Static forecasting extends the forward recursion through the end of the estimation sample, al- lowing for a series of one-step ahead forecasts of both the structural model and the innovations. When compu- ting static forecasts, EViews uses the entire estimation sample to backcast the innovations [16]. In Figure 2, the graph of actual hourly EVN traffic stream is plotted using a solid red line and while blue line represents the forecasted hourly EVN traffic stream by ARIMA (1, 0, 1) × (0, 1, 1)24. The forecast series follow the actual series closely. In the next step, the heteroscedasticity test is implemented and it shows that our traffic data contains volatility periods. Thus, we can proceed to build GARCH model based on the multiplicative seasonal ARIMA model that we achieved. Following the steps mentioned above, GARCH (1, 1) assuming GED formulates which has the smallest measure of forecast error, i.e. MAE and RMSE, should be chosen as the one with the most accurate fit of the time series model. MAE indicates that the average difference between the forecast and the observed value of the model is 0.080042, while RMSE and MAPE are 0.131390 and 276.0843, respectively. Figure 2. The plot of actual values and forecast values by ARIMA (1, 0, 1) × (0, 1, 1)24 model. 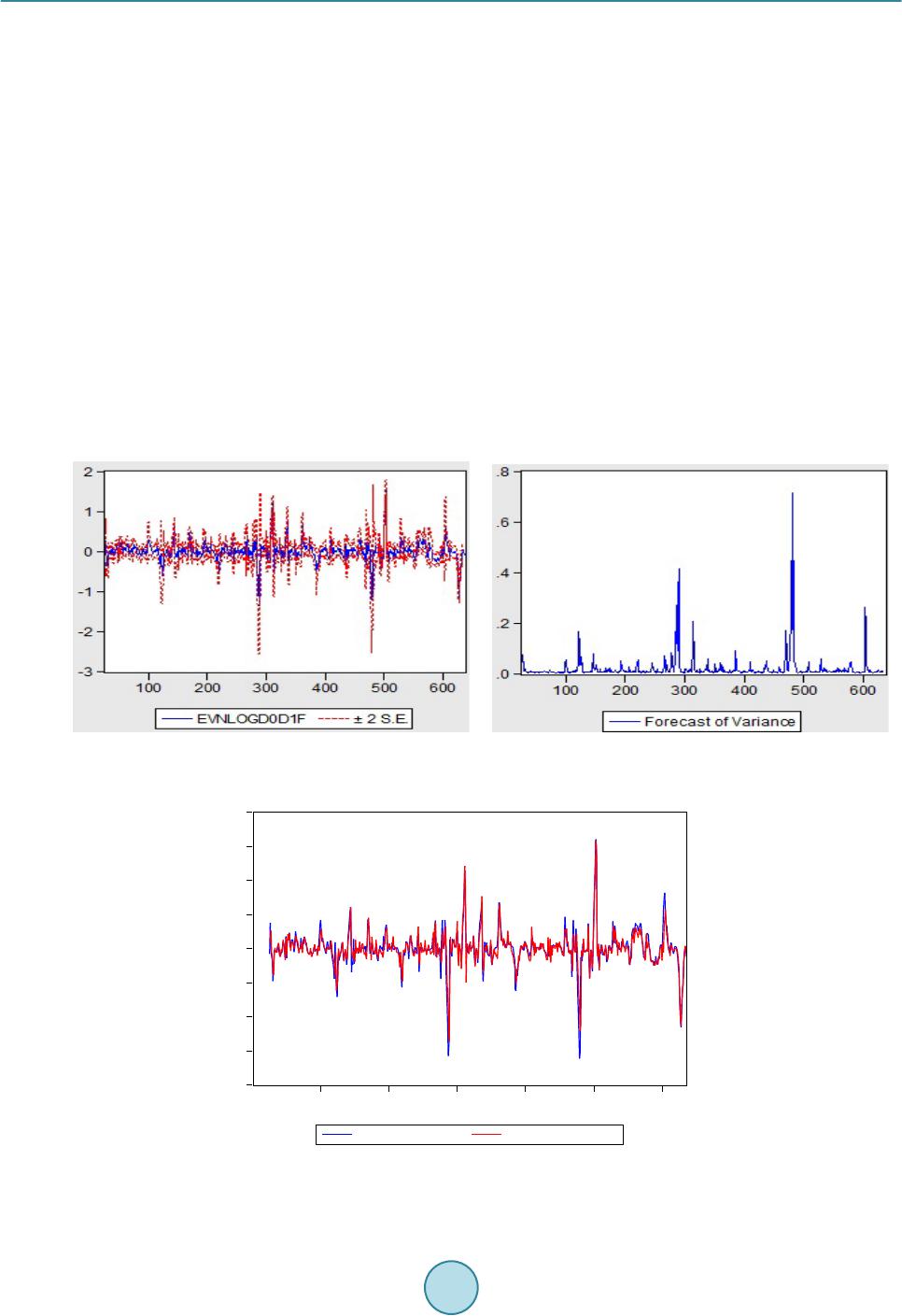 Q. T. Tran et al. Incorporating the most adequate choice for the volatility model, we now present the forecast for the mean and error variance of the EVN traffic, as shown in Figure 3 using the in-sample observations under static forecasting. The figure implies that volatile values are evident during the values between about 280 to 290 and 480 to 490. This is evident in the wide confidence intervals on the GARCH model under the forecast of mean. For the other values, however, we observe a stable and predictable traffic, as shown in the low values of the forecast of error variance. Furthermore, some other tests are also implemented to make our decision more convincing. In this case, the correlogram of standardized residuals squared once again proves that the model is adequate, and the ARCH-LM test on the residuals of this model indicates that the conditional heteroscedasticity is no longer present in the da- ta. Next we plot the actual and forecast EVN traffic value by ARIMA (1, 0, 1) × (0, 1, 1)24/GARCH (1, 1) model. From Figure 4, it can be concluded that the trend of forecast values follows the actual EVN traffic values closely. In the final step, we will evaluate our ARIMA (1, 0, 1) ×(0, 1, 1)24/GARCH (1, 1) model in terms of AIC and SIC values in the estimation stage, and forecast performances in the forecasting stage. a) Information Criterion for ARIMA (1, 0, 1) × (0, 1, 1)24/GARCH (1, 1) Models In the model estimation step, the AIC and SIC values from ARIMA (1, 0, 1) × (0, 1, 1)24/GARCH (1, 1) mod- el is calculated. According to our criterion, the smaller AIC and SIC values, the better model defined. The re- sults are tabulated in Table 1. Figure 3. ARIMA (1, 0, 1) × (0, 1, 1)24/GARCH (1, 1) model forecast for the mean and error variance of EVN traffic using the in-sample observations under static forecasting. Figure 4. The plot of actual traffic against forecast traffic by ARIMA (1, 0, 1) × (0, 1, 1)24/GARCH (1, 1) model. -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 1.5 2.0 100 200 300 400 500 600 EVNLOGD0D1 EVNLOGD0D1F  Q. T. Tran et al. In Table 1, AIC and SIC values obtained from the equation estimation of ARIMA (1, 0, 1) × (0, 1, 1)24/- GARCH (1, 1) model using EViews are shown together with those of ARIMA (1, 0, 1) × (0, 1, 1)24 model which is a part of our ARIMA (1, 0, 1) × (0, 1, 1)24/GARCH (1, 1) model. The AIC and SIC of ARIMA (1, 0, 1) × (0, 1, 1)24/GARCH (1, 1) are -1.9226 and -1.8721, respectively, which can be found smaller than those of ARIMA (1, 0, 1) × (0, 1, 1)24 model, i.e.-1.2187 and -1.1970, respectively. This result shows that the GARCH part presents a positive influence and makes our ARIMA (1, 0, 1) × (0, 1, 1)24/GARCH (1, 1) model built in a reasonable way. b) Forecasting Performance of ARIMA (1, 0, 1) ×(0, 1, 1)24/GARCH (1, 1) Model The forecasting performance is evaluated via forecasting statistics that tabulated in Figure 5. The smaller those values are, the better forecasting performance obtained. The statistics in Figure 5 show that our ARIMA (1, 0, 1) ×(0, 1, 1)24/GARCH (1, 1) model presents a reasonable result in forecasting EVN traffic series. 4. Conclusions In our study, a multiplicative seasonal ARIMA/GARCH model, i.e. ARIMA (1, 0, 1) × (0, 1, 1)24/GARCH (1, 1), shows a good result in describing and forecasting our mobile communication network traffic. The mobile traffic is found containing volatility periods. Therefore, the ARIMA (1, 0, 1) × (0, 1, 1)24 model is firstly formed to present the mean components, and then the GARCH (1, 1) model is incorporated to deal with the volatility of the traffic. The evaluation of the estimation criterions shows that our ARIMA (1, 0, 1) × (0, 1, 1)24/GARCH (1, 1) was built reason-ably with a significant impact of the GARCH part. And also the forecasting performance evaluation presents small forecasting error values that confirm the capable of fitting and forecasting the traffic of our model. Moreover, as a part of our model, ARIMA (1, 0, 1) × (0, 1, 1)24 also present a relatively good result when conducting to fit and forecast the traffic. Based on this, we can conclude that in short-term prediction, where the volatility even occurs but has an insignificant impact on the whole result of forecast, our multiplicative seasonal ARIMA/GARCH model can be simplified as a multiplicative seasonal ARIMA model, by adjusting the para- meter of the GARCH part, i.e. GARCH (0, 0). In conclusion, our multiplicative seasonal ARIMA/GARCH model is a flexible model which is capable of fitting and forecasting mobile traffic not only in short-term predic- tion but also in long-term prediction. Acknowledgements This work was supported in part by the Young Innovative Research Team of Sichuan Province under Grant Figure 5. Forecasting performances of ARIMA (1, 0, 1) × (0, 1, 1)24/ GARCH (1, 1) model. Table 1. Information criterion for ARIMA (1, 0, 1) × (0, 1, 1)24/GARCH (1, 1) and ARIMA (1, 0, 1) × (0, 1, 1)24 models. Model AIC SIC ARIMA (1, 0, 1) × (0, 1, 1)24/GARCH (1, 1) −1.9226 −1.8721 ARIMA (1, 0, 1) × (0, 1, 1)24 −1.2187 −1.1970  Q. T. Tran et al. 2011JTD0007, and by the Fundamental Research Funds for the Central Universities under Grant SWJTU12CX004, SWJTU12ZT02. References [1] Shu, Y.T., Yu, M.F., Liu, J.K. and Yang, O.W.W. (2003) Wireless Traffic Modeling and Prediction Using Seasonal ARIMA Models. IEE E. [2] Yu, Y.H., Wang, J., Song, M.N. and Song, J.D. (2010) Network Traffic Prediction and Result Analysis Based on Sea- sonal ARIMA and Correlation Coefficient. 2010 International Conference on Intelligent System Design and Engineer- ing Application. http://dx.doi.org/10.1109/ISDEA.2010.335 [3] Guo, J., Peng, Y., Peng, X.Y., Chen, Q., Yu, J. and Dai, Y.F. (2009) Traffic Forecasting for Mobile Networks with Multiplicative Seasonal ARIMA Models. The Ninth International Conference on Electronic Measurement & Instru- ments. [4] Chen, H., Wan, Q.L., Zhang, B., Li, F.X. and Wang, Y.R. (2010) Short-Term Load Forecasting Based on Asymmetric ARCH Models. IEEE. [5] Chen, C.Y., Hu, J.M., Meng, Q. and Zhang, Y. (2011) Short-Time Traffic Flow Prediction with ARIMA-GARCH Model. IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, 5-9 June. [6] Zhou, B., He, D. and Sun, Z.L. (2006) Traffic Predictability Based on ARIMA/GARCH Model. 2nd Conference on Next Generation Internet Design and Engineering. [7] Radha, S. and Thenmozhi, M. (2006) Forecasting Short Term Interest Rates Using ARMA, ARMA-GARCH and ARMA-EGARCH Models. [8] Nian, L.C. (2009) Application of ARIMA and GARCH Models in Forecasting Crude Oil Prices. A Dissertation Sub- mitted in Partial Fulfillment of the Requirement for the Award of the Degree of Master of Science (Mathematics). [9] Ramon, H.L. (2008) Forecasting the Volatility of Philippine Inflation Using GARCH Models. BSP Working Paper Se- ries, Series No. 2008-01. [10] Kim, S. (2011) Forecasting Internet Traffic by Using Seasonal GARCH Models. Journal of Communications and Net- works, 13. http://dx.doi.org/10.1109/JCN.2011.6157478 [11] Dong, N.Q. (2008) Econometrics—Advanced Program. Science and Technique Publisher. [12] Dong, N.Q. (2008) Econometrics Assignments—With EVIEWS. Science and Technique Publisher. [13] Quynh, N.H. (2004) Time Series Analysis and Identification. Science and Technique Publisher. [14] Agung, I.G.N. (2009) Time Series Data Analysis Using EViews. John Wiley & Sons (Asia) Pte Ltd. [15] (2007) EViews 6 User’s Guide I. Quantitative Micro Software, LLC. [16] (2007) EViews 6 User’s Guide II. Quantitative Micro Software, LLC.
|