Optics and Photonics Journal, 2011, 1, 75-80
doi:10.4236/opj.2011.12012 Published Online June 2011 (http://www.SciRP.org/journal/opj/)
First-Principles Study of the Optical Properties of SrHfO3
H. Salehi, H. Tolabinejad
Department of Physics, Shahid Chamran University of Ahvaz, Ahvaz, Iran
Received March 17, 2011; revised April 15, 2011; accepted April 25, 2011
Abstract
The optical properties of SrHfO3 were studied by first principle using the density functional theory. The di-
electric functions and optical constants are calculated using the full potential—linearized augmented plane
wave (FP-LAPW) method with the generalized gradient approximation (GGA) by Wien2k package. The
theoretical calculated optical properties and energy loss (EEL) spectrum yield a static refractive index of 1.
924 and a Plasmon energy of 27 eVfor cubic phase. The complex dielectric functions are calculated which
are in good agreement with the available experimental results.
Keywords: Optical Properties, SrHfO3, WIEN2k, FP-LAPW, DFT, GGA
1. Introduction
The development of computational methods in the elec-
tronic-structure community has led to a new class of first
principles approaches, based upon a full solution of the
quantum mechanical ground state of the electron system
within the local-density approximation(LDA)to Kohn-
Sham density functional theory (DFT) [1,2]. In principle,
these methods take as their only inputs the atomic num-
bers of the constituent atoms.The modeling of electronic
and optical properties, by means of first-principles cal-
culations, has become a very useful tool for understand-
ing about the structural, electronic and optical properties
of the various materials.
A particularly successful application of this technique
has been its use in understanding the Perovskite ferro-
electric Compounds. SrHfO3 is a typical perovskite di-
electric with a wide rang of technological applications.
Because of its special properties related to ferroelectric-
ity, semi conductivity.SrHfO3 is a Compound that has a
Composition and lattice structure similar to SrTiO3. Al-
though the perovskite Compound SrHfO3 has been will
known for along time, theoretical studies on this com-
pound are few [3]. Material with structure ABO3 have
been the subject of extensive investigation, because of
the unusual combination of their magnetic, electronic
and transport properties[4,5].Their use in technological
applications is also diverse, including optical wave guides,
laser-host crystals, high temperature oxygen sensors,
high-voltage capacitor, piezoelectric materials in actua-
tors and so on [6,7]. Recently, stachiotti et al. [8] inves-
tigated its ferroelectric instability by first–principles cal-
culation. First-Principles calculation is one if the power-
ful tools for carrying out the theoretical studies of the
electronic and structure properties of materials. The-
ABO3 Perovskite type oxides have potentials to be at-
tractive functional materials because of their various
unique Properties. Among them, alkaline. Rear-earth haf
nates, (AHfO3, A = Ba, Sr or Ca) have been reported [3,9]
as promising Candidates as scintillators used in γ-ray
imaging fields, such as positron emission tomography.
Besides, SrHfO3 is a promising candidate high-k dielec-
tric oxide for the next generation of CMDS devices, due
to its good physical and electrical Properties [10].
Kennedy et al. [11] concluded that SrHfO3 undergoes
three phase transitions: From 300 k to approximately 670
k the structure of SrHfO3 is orthorhombic with space
group Pnma. By 870 k it adopts a second orthorhombic
structure with space group Cmcm. Its then undergoes a
further phase transition and is tetragonal with space
group 14/mcm from 1000 to 1353 k. At higher tempera-
ture the structure is the ideal cubic perovskite with space
group Pm 3 m. In the present work the optical proper-
ties of SrHfO3 in cubic phase have been studied using the
FP-LAPW method. The results, in comparison with the
previous theoretical data, are in better agreement with the
experimental results.
2. Method of Calculation
Calculation of the optical properties, of SrHfO3 were
carried out with a self-consistent scheme by solving the

H. SALEHI ET AL.
76
Kohn-Sham Equation using aFP-LAPW method in the
framework of theDFT along with the GGA method [12,
13] by WIEN2k package [14]. In the FP-LAPW method,
space is divided into two regions, a spherical “muffin-tin”
around the nuclei in which radial solutions of Schrö-
dinger Equation and their energy derivatives are used as
basis functions, and an “interstitial” region between the
muffin tins (MT) in which the basis set consists of plane
waves. There is no pseudopotential approximation and
core states are calculated self-consistently in the crystal
potential. Also, core states are treated fully relativisti-
cally while valence and semi-core states are treated semi-
relativistically (i.e. ignoring the spin-orbit coupling). The
cut-off energy, which defines the separation of the core
and valance states, was chosen as –6 Ry. The complex
dielectric tensor was calculated, in this program, accord-
ing to the well-known relations [15].
2
22
c
,
4e
Im( )
d|| ||δ(ε)
αβ
v
cv
mω
kc pvv pcεω





kk
kkkk
(1)
22
0
Im( )
2
Re()dP

 


 




 

 (2)
And the optical conductivity is given by:
Re( )Im()
4
 


  (3)
In Equation (1), ck and vk are the crystal wave func-
tions corresponding to the conduction and the valance
bands with crystal wave vector k. In Equation (3) the
conductivity tensor relating the interband current density
j in the direction which flows upon application of an
electric field E in direction in which the sum in Equa-
tion (1) is over all valence and conduction band states
labeled by v and c. Moreover, the complex dielectric
constant of a solid is given as:
12
() ()()i

   (4)
Here, real and imaginary parts are related to optical
constants

n

and

k

as:
22
1
2
()()()
() 2()()
nk
nk


 

 (5)
The other optical parameters, such as energy-loss spec-
trum and oscillator strength sum rule are immediately
calculated in terms of the components of the complex
dielectric function [15].
3. Results and Discussion
The calculations first were carried out using the experi-
mental data for lattice constants (a = 7.78 a.u) [8] in the
cubic phase. Then by minimizing the ratio of the total
energy of the crystal to its volume (volume optimizing)
the theoretical lattice constants were obtained (a = 7.87
au). In order to reduce the time of the calculations we
used the symmetries of the crystal structure and some
other approximations for simplicity.The calculation was
performed with 1000 k-points inthe cubic phase.
The self-consistent process, for both phases, after 11
cycles had convergence of about 0.0001 in the eigenval-
ues in which for the cubic phase 388 plane waves were
produced. Under these conditions the values of the other
parameters were Gmax = 14, RMT(Sr) = 2 au, RMT(Hf) =
2.2 au, RMT(O) = 1.5 au. The iteration halted when the
total charge adjustment was less than 0.0001 between
steps.
3.1. Dielectric Function
In WIEN2K calculations for finding optical functions,
reflactions of kramers-kronig was used. As an example
in transformation kramers-kronig, without coupling spin-
orbit and magnetic field, the dielectric tensor cubic struc-
ture is as follows:
Im0 0
0Im0kramers kronig
00Im
Re00
0Re0
00Re
xx
xx
xx
xx
xx
xx


















(6)
In this theoretical method, momentum matrix elements,
for finding dielectric function and other optical proper-
ties Equation (3) is used. Because it has hexagonal
closed packed structure (hcp), so due to tensor form for
this structure, the selections
x
x

(dielectric function in
direction x) and
z
z

(dielectric function in direction
z)are enough for calculating dielectric tensor.
We calculated optical properties of SrHfO3 in the cu-
bic phase. The real and the imaginary parts of the dielec-
tric functions are shown in Figure 1 for SrHfO3in the
cubic phase. In Figure, there are mainly four peaks (5.5,
7, 9.5 and 12 eV). Peaks A (5.5 eV), B(7 eV)correspond
mainly to the transitions from O 2p to Hf 5d states along
the

direction, and peaks C(9.5 eV), D(12 eV) corre-
spond mainly to the transitions from semicore bands
(formed by Sr- 4p and O- 2s states) to conduction bands.
The value of the main peak of

1


curve is6 at en-
ergy of 5.5 eV and for


2


is 6.4 at the energy equal
4 eV.
Figure 1 shows the change of Re( )
xx

(Real part of
dielectric function in the x direction) against photons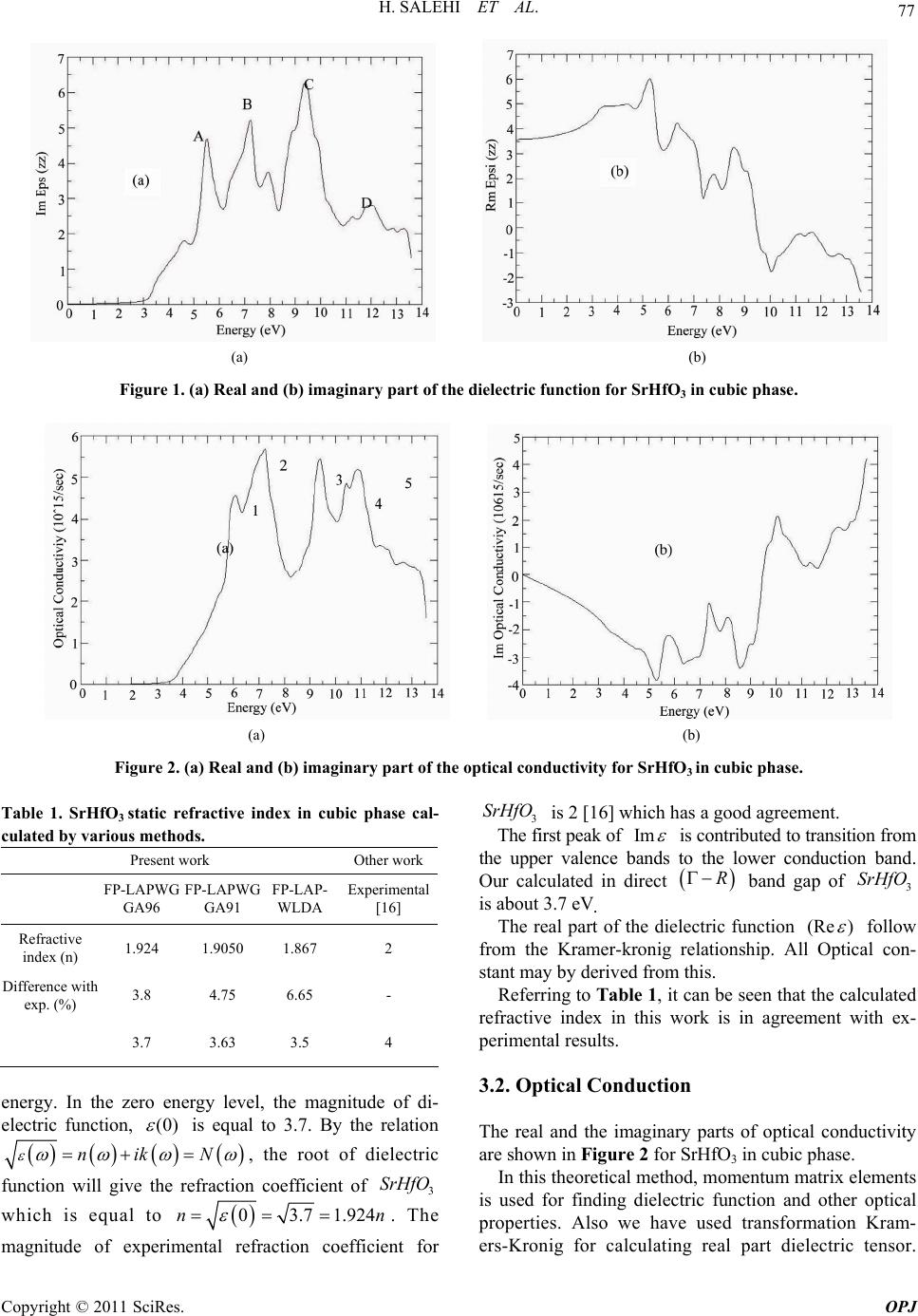

H. SALEHI ET AL.
77
(a) (b)
Figure 1. (a) Real and (b) imaginary part of the dielectric function for SrHfO3 in cubic phase.
(a) (b)
Figure 2. (a) Real and (b) imaginary part of the optical conductivity for SrHfO3 in cubic phase.
Table 1. SrHfO3 static refractive index in cubic phase cal-
culated by various methods.
Present work Other work
FP-LAPWG
GA96
FP-LAPWG
GA91
FP-LAP-
WLDA
Experimental
[16]
Refractive
index (n) 1.924 1.9050 1.867 2
Difference with
exp. (%) 3.8 4.75 6.65 -
3.7 3.63 3.5 4
energy. In the zero energy level, the magnitude of di-
electric function, (0)

is equal to 3.7. By the relation
 
nik N 

   , the root of dielectric
function will give the refraction coefficient of 3
SrHfO
which is equal to

03.7 1.924nn  . The
magnitude of experimental refraction coefficient for
3
SrHfO is 2 [16] which has a good agreement.
The first peak of Im

is contributed to transition from
the upper valence bands to the lower conduction band.
Our calculated in direct


R

 band gap of 3 SrHfO
is about 3.7 eV.
The real part of the dielectric function (Re )

follow
from the Kramer-kronig relationship. All Optical con-
stant may by derived from this.
Referring to Table 1 , it can be seen that the calculated
refractive index in this work is in agreement with ex-
perimental results.
3.2. Optical Conduction
The real and the imaginary parts of optical conductivity
are shown in Figure 2 for SrHfO3 in cubic phase.
In this theoretical method, momentum matrix elements
is used for finding dielectric function and other optical
properties. Also we have used transformation Kram-
ers-Kronig for calculating real part dielectric tensor.

H. SALEHI ET AL.
78
Notice that, occupied electron states are excited to unoc-
cupied electron states in upper Fermi level by absorbing
photons.This interband transition is called optical con-
duction (also called Drude transition) and photon absorp-
tion by electron is called interband absorption.
Figure 4 shows the change of real part of optical con-
duction (in1015 s-1) in the X direction with respect to in-
ternal photon energy. As in the Figure 2, the optical
conduction starts with energy of about 2eV and by in-
creasing photon energy, the optical conduction will
rises and in the range of 6.5 till 7 eV, will reach to the
upper level. The reason of starting optical conduction,
()

 , from 2eV energy, is the gap of energy. So the ex-
cited electrons have no enough energy to pass the energy
gap, and transfer to the conduction band.
For the absorption coefficient, ()

 , the absorption
edge start from about 3.4 eV, corresponding to the direct
 transition. The maximum reflectivity about13eV,
ie the minimum value 1

will occur. In the regime in-
cident beam energy, has not been reached to create a new
exaction mode yet or can prepar interband transition and
thus waves will be completely reflectivity.
The peak function ()

 also in energy 11.5 eV can
be seen, and with this mean the most value absorption in
the band gap, which the matter cannot exhibit any trans-
parency.
In Figure 3 the optical parameters is shown for SrHfO3
in cubic phase. The static refractive index value for
SrHfO3 in the cubic phase calculated in this work, and
the values obtained by other methods are summarized in
Table 1.
If we assume assume orientation of the crystal surface
parallel to the optical axis, the reflectivity ()R

fol-
lows directly from Fresnels formula.
2
() 1
() () 1 R



 (7)
Expression for the absorption coefficient ()I

now
follow:

1/2
22
121
() 2()()()()I    (8)
3.3. Electron Energy Loss Spectroscopy
EELS is a valuable tool for investigating various aspects
of materials. It has the advantage of covering the complete
energy range including non-scattered and elastically
Tabel 2. The value transition interband.
Transition First Two Three Four Five
E(eV) 5.5 6.7 9.5 10.5 11.2
scattered electrons (Zero Loss). At intermediate energies
(typically1 to50 eV) the energy losses are due primarily to
a complicated mixture of single electron excitations and
collective excitations (plasmons). The positions of the sin-
gle electron excitation peaks are related to the joint density
of states between the conduction and valence bands,
whereas the energy required for the excitation of bulk
plasmons depends mainly on the electron density in the
solid. Here electrons, which excite the atoms electrons of
the outer shell is called Valence Loss or valence intera-
band transitions. At higher energies, typically a few hun-
dred eV, edges can be seen in the spectrum, indicating the
onset of excitations from the various inner atomic shells to
the conduction band.In this case the fast electrons excite
the inner shell electrons (Core Loss)or induce core level
excitation of Near Edge Structure (ELNES) and XANES.
The edges are characteristic of particular elements and
their energy and height can be used for elemental analysis.
In the case of interband transitions, which consist
mostly of plasmon excitations, the scattering probability
for volume losses is directly connected to the energy loss
function. One can then calculate the EEL spectrum from
the following relations.
12
2
22
12
()i and
EELSpectrumIm[1/()]


 





 

(9)
These peaks can, however, have different origins such
as charge carrier plasmons and interband or intraband
excitations. The energy of the maximum peak of Im


1







 at 27 eV is assigned to the energy of the
volume plasmon p

. The first peak at 9 eV and second
peak at 13eV originates from O-2p to Hf-3d and Sr-p or-
bitals, respectively Figure 4. The value of
p

 obtained
in this work and for free electron is given in Table 3.
For free electrons the plasmon energy is calculated
according to the following model:
2
0
e
p
ne
m


 (10)
If we use this model, then what should be the number
of valance electrons per SrHfO3 molecule, N, used to
calculate the density of valance electrons, n, and thus the
plasmon energy in Equation (7). If we take only the con-
tribution of 4s2, 4p6 and 5s2 electrons of Sr, 5s2, 5p6, 5d10
and 6s2of Hf and2s2, 2p4 of O(ignoring the contribution
of 5s2 and 2s2 electron of Sr and O atom respectively)
and the free and electron plasmon energy will be 31eV.
Otherwise, with all valance electrons of Sr, Hf and O
atoms, the free electron plasmon would be 38.6eV. We
will also see from sum rule is a reasonable value for the
valance electrons per SrHfO3 molecule.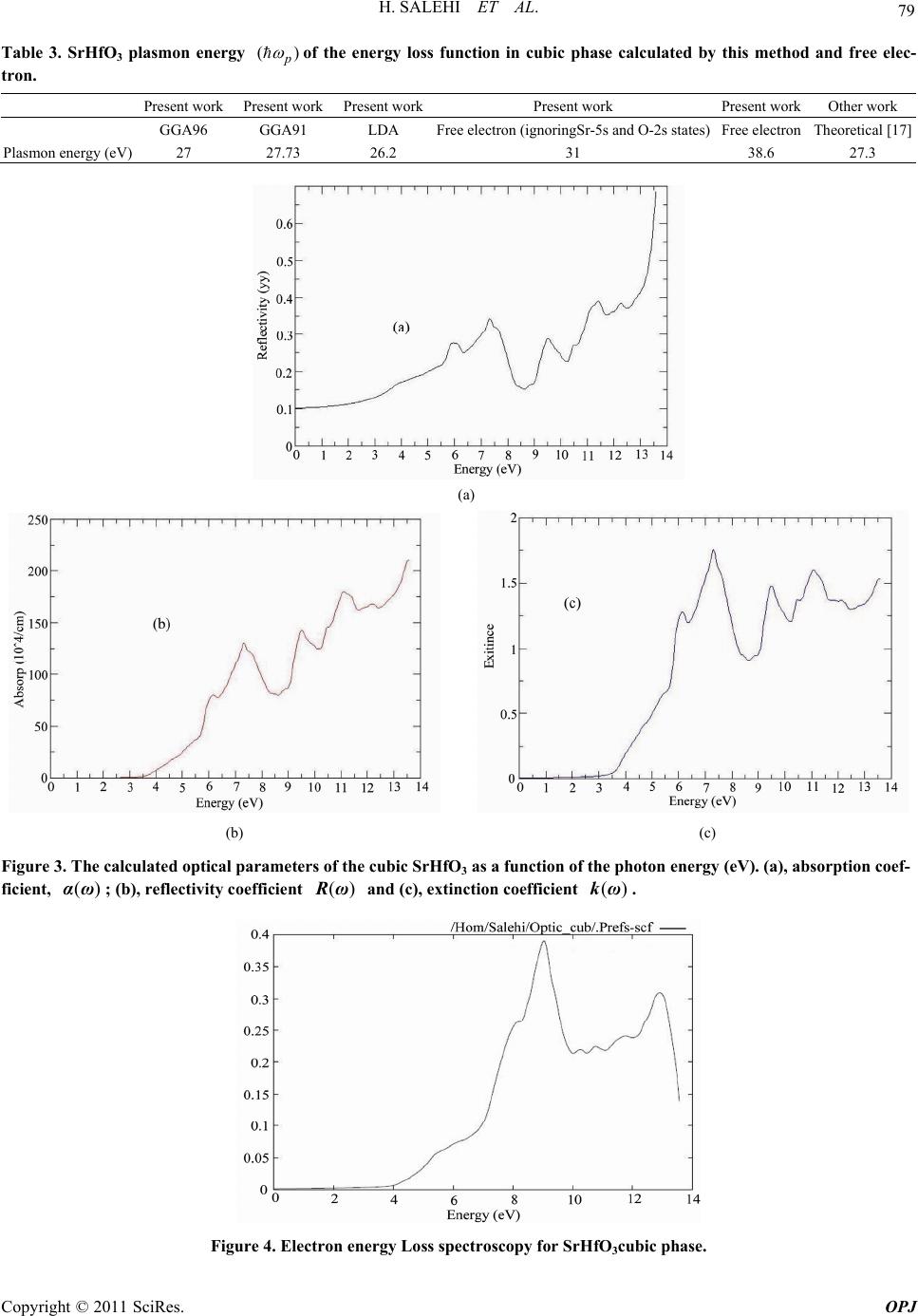

H. SALEHI ET AL.
79
Table 3. SrHfO3 plasmon energy ()
p

of the energy loss function in cubic phase calculated by this method and free elec-
tron.
Present work Present work Present workPresent work Present work Other work
GGA96 GGA91 LDA Free electron (ignoringSr-5s and O-2s states) Free electron Theoretical [17]
Plasmon energy (eV) 27 27.73 26.2 31 38.6 27.3
(a)
(b) (c)
Figure 3. The calculated optical parameters of the cubic SrHfO3 as a function of the photon energy (eV). (a), absorption coef-
ficient, ()αω ; (b), reflectivity coefficient ()Rω and (c), extinction coefficient ()kω.
Figure 4. Electron energy Loss spectroscopy for SrHfO3cubic phase.

H. SALEHI ET AL.
80
4. Conclusions
We have calculated the optical properties of SrHfO3 in
cubic phases using the FP-LAPW method with the gen-
eralized gradient approximation (GGA). Thecalculations
show a static refractive index of 1.924 and an EEL spec-
trum of 27eV for the cubic phase. Ignoring the contribu-
tion of 5s2 and 2s2 electron of Sr and O atom respectively,
the free electron plasmon energy will be 38.6 eV. It
seems that is a reasonable value for the valance electrons
per molecule. The calculated results show a good agree-
ment with the other data.
5. References
[1] J. P. Perdew, J. A. Chevary, et al., Phys.Rev.B, Vol. 46,
No. , 1992, pp. 6671-6687.
[2] J. P. Perdew, Physical. B, Vol. 172, No. , 1991, pp. 1-6.
[3] Y. M. Ji, D. Y. Jiang, Z. H. Wu, T. Feng and J. L. Shi,
Mater.Res.Bull., Vol. 40, No. , 2005, pp. 1521
[4] I. R. Shein, V. L. Kozhevnikov and A. L. Ivanovskii,
Solid State Sci. Vol.10, No. , 2008, pp. 217.
[5] C. M. I. Okoye, J. Phys.: Condens. Matter, Vol. 15, No. ,
2003, pp. 5945.
[6] S. Lin, Z. Xiu, J. Liu, F. Xu, W. Yu, J. Yu and G. Feng, J.
Alloy. Compd, Vol. 457, No. , 2008, pp. L12.
[7] V. M. Longo, L. S. Cavalcante, A. T. de Figneiredo, L. P.
Santos, E. Longo, J. A. Varela, J. R. Sambrano, C. A.
Paskocimas, F. S. De Vicente and A. C. Hernandes, Appl.
Phys. Lett. Vol. 90, No. , 2007, pp. 091906.
[8] M. G. Stachiotti, G. Fabricius, R. Alonso and C. O. Rod-
riguet, Phys.Rev.B, Vol. 58, No. , 1998, pp. 8145.
[9] R. Vali, Solid State Communications, Vol. 148, No. ,
2008, pp. 29-31.
[10] C. Rossel, M. sousa, C. Marchiori, et al. Microelec. Eng
Vol. 84, No. , 2007, pp. 1869.
[11] B. J. Kennedy, C. J. Howard and B. C. Chakoumakos,
Phys.Rev.B, Vol. 60, No. , 1999, pp. 2972.
[12] J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson,
M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B
Vol. 46, No. , 1992, pp. 6671-6687.
[13] M. Peterson, F. Wanger, L. Hufnagel, M. Scheffler, P.
Blaha and K. Schwarz, Computer Physics Communica-
tions, 126, (2000) 294-309.
doi:10.1016/S0010-4655(99)00495-6
[14] P. Blaha and K. Schwarz, WIEN2k, Vienna University of
Technology Austria, 2009.
[15] F. Wooten, “Optical Properties of Solids,” Academic
Press, New York, 1972.
[16] M. Sousa, C. Rossel, C. Marchiori, D. Caimi, J. P. Loc-
quet, D. J. Webb, K. Babich, J. W. Seo and C. Dieker, J.
Appl. Phys. Vol. 102, No. , 2007, pp. 104103.
[17] Z. Feng, H. ShouxinCui and C. HengshuaiLi, Journal of
Physics and Chemistry of Solids Vol. 70 No. , 2009, pp.
412-416.