Optics and Photonics Journal, 2011, 1, 65-69
doi:10.4236/opj.2011.12010 Published Online June 2011 (http://www.SciRP.org/journal/opj/)
ZnSe/ZnS Quantum-Dot Semiconductor
Optical Amplifiers
K. H. Al-Mossawi
Scholarships & Cultural Affairs, Ministry of Higher Education & Scientific Research, Iraq
Received April 5, 2011; revised May 7, 2011; accepted May 17, 2011
Abstract
ZnSe quantum dot (QD) semiconductor optical amplifier (SOA) is studied theoretically using net gain for
linear Absorption coefficient and linear emission and these results are used to calculate noise figure and
small-signal gain.
Keywords: Linear Absorption Coefficient, Linear Emission Coefficient, Rate Equations (Res), Noise Figure
1. Introduction
Quantum dot photonic materials have attracted much
attention in recent years as they have the potential to
deliver the stability and coherence of atomic sources
within a compact and efficient semiconductor device.
characteristics such as reduced sensitivity to optical feed-
back makes such materials attractive as laser sources. In
addition, suppression of pattern effects in QD semicon-
ductor optical amplifiers (SOAs) shown to be promises
for high speed application. The understanding of the high
speed carrier dynamics of these materials is crucial for
their optimization and exploitation. To address this issue,
time resolved spectroscopy has been used to investigate
the fundamental carrier decay time scales of SOA struc-
tures and determine their suitability for high-speed ap-
plications. Such pump-probe studies are usually per-
formed using pulse width of a few hundred femtoseconds
to picoseconds in order to sufficiently resolve the relaxa-
tion dynamics of high-speed devices. [1] Quantum dot
(QD) semiconductor optical amplifiers (SOAs) demon-
strate best features when compared with other SOAs
based on bulk or quantum well materials. As a result, QD
SOAs are very promising for applications in high-speed
optical communications. One of the most important fea-
tures of QD materials results in these best performances
is the discrete structure of their energy levels [2].
In this work, ZnSe/ZnS QD-SOAs are studied. First,
energy levels are calculated using quantum box model
where the dot is assumed in the form a cube with quan-
tum dot size is 10 × 10 × 10 nm3. net gain is then calcu-
lated by using linear Absorption coefficient and linear
emission coefficient components in the QD.
2. Gain of QDs
Gain and threshold current models are calculated with
quasi-Fermi levels energies Efc and Efv, which are di-
rectly controlled by the doping concentration or injected
current. Given that wx, wy and wz are the lengths in each
dimension of a quantum box, see Figure 1, and Ecnml and
Evnml are allowed quantized electron and hole energies,
respectively, the corresponding carrier densities, n and
p(~n) may be expressed as [3]


22
1exp c
c cnml
nml nml
xyz cnml f
x
yz
fE
nwww EE
www
kT




 



 (1)




21 2
1exp v
vvnml
nml nml
xyz fcnml
x
yz
fE
pwww EE www
kT





 



 (2)
Figure 1. Diagram of dot/barrier quantum box.
wx
wy
wz
barrier
dot

K. H. AL-MOSSAWI ET AL.
66
Where fc and fv are the corresponding Fermi functions
for electrons in the conduction and valence bands. The
factor of two takes into account the electron spin. The
summation is over all the confined energy states, which
depends on the QD material and the dot/barrier valence
and conduction band offsets (ΔEc and ΔEv) that enable
electron and hole confinement. Solving known Efc and
Efv are ed for directly and applied to find the linear ab-
sorption coefficient α(w) and linear emission coefficient
e(w) components in the QD [3]

 

12
2
2
2
1
d
g
cv vc
in
o
cv cv
nml
roE
cv
in
h
gf Ef E
w
aw RE
nh
Ehw






 








(3)

 

21
2
2
2
1
d
g
cv cv
in
o
cv cv
nml
roE
cv
in
h
gf Ef E
w
ew RE
nh
Ehw






 








(4)
Where Rcv is the dipole moment, nr is the refractive
index and gcv is the density of states for the QD, given by
[3]

2cv cnmlg
cv
xyz
EE E
gwww
 
 (5)
Where τin the intraband relaxation time. Equations (3)
and (4) signify the rates of absorption and emission per
unit length with E1 and E2 representing the hole energy
level in the valence band and the electron energy level in
the conduction band, respectively. The net gain of the
system is then [3]
  
Gwew aw (6)
To determine the optimal operating region for an am-
plifier system, the gain coefficient, expressed as [3]

in
Gw
gaincoefficientP  (7)
3. QD-SOA
Based on the rate equations used in [4] for the wetting
layer (WL) carrier density Nw, occupation probabilities
for ground and exited states (f and h), respectively one
can write.

22
1
w
www
ww wwR
Nh
NNhN J
tqL



 
 (8)



22 2112
111
ww ww
QwQ w
NLhf hfh
NLh
h
tN N 


 (9)




2
2112 1
11 21
p
av
RQ s
gL
fh fh
ffc
fS
tN
 



 
(10)
Where J is the current density, q is the electron charge,
Lw is the effective thickness of the active layer, τw2 is the
carrier relaxation time from the two-dimensional WL to
the ES, τ2w is the carrier escape time from the ES to the
WL, τwR is the spontaneous radiative lifetime in WL,
τ1R is the spontaneous radiative lifetime in the QDs, τ21
is the carrier relaxation time from ES to GS, τ12 is the
carrier relaxation time from the GS to the ES, NQ is the
surface density of QDs, εs is the dielectric constant of the
QD material and Г is the optical confinement factor. gp is
the peak material gain. According to Pauli's exclusion
principle, the occupation probability in the quantum-dot
ground state relates to the carrier density N in the QD by
f = N/2(NQ/wx) [5] where wx is the size of the QD. The
average signal photon density Sav is given by [6]
  

22
11 1
14sin
fb in g
av
p
wp
fb fb
GRRG Pn
Shw L DLgc
RRG RRG


 





(11)
Where Pin is the input signal power, ng is the group re-
fractive index, ћ is the normalized Plank’s constant, wp is
the peak frequency, D is the width of the active layer, L
is the cavity length, c is the free space light speed. Note
that the Fibry-Perot amplifier gain G is given by [7]





22
11
14sin
fbS
fbs fbs
RRG
G
RRG RRG 



(12)
Rf is the front mirror reflectivity, Rb the back mirror
reflectivity. Φ is the phase angle while GS is the sin-
gle-pass gain of the structure, given by [7]


int
exp
sp
GgaL




 (13)
Note that αint is the loss coefficient. The carrier dy-
namics described by the rate Equations are related only
to electrons in the conduction band while hole dynamics
can be neglected due to their larger effective mass [4]. In
addition, typical values of the material parameters in
Table 1 [5] for ZnSe/ZnS system where (Eg = 2.8 eV, me
= 0.17 mo and mv = 0.60 mo) for ZnSe and (Eg = 3.68 eV,
me = 0.39 mo and mv = 0.49 mo) for ZnS.
Rate equations model are solved at steady state case
using the expression of the average signal photon density
Sav, Equation (11). The noise added to the signal during
the amplification process is a fundamental property for
every kind of amplifiers. The noise characteristics of an
amplifier are quantified by a parameter called noise fig-
ure, when the shot noise part is taken into account, the
amplifier noise figure can be written as [7].

K. H. AL-MOSSAWI ET AL.
67
Table 1. Parameters used in the Calculations [5].
Parameter Value Unit
L 200 μm
Lw 0.2 μm
D 10 μm
NQ 5 × 1010 cm-2
τw2 3 ps
τ2w 1 ns
τ12 1.2 ps
τ21 0.16 ps
τ1R 0.4 ns
τwR 1 ns
Φ 0
Rf = Rb 10–4
αint 3 1/cm
Γ 0.006
Lb 20 nm
Lc 75 nm
Pin 1 μW
 
21/1/
nsp
F
nG G G (14)
The the spontaneous emission factor nsp is given by [8]



int
sp
ew
nGw a




(15)
4. Results and Discussion
Using quantum box model we calculate QD energy lev-
els for conduction and valence bands and then it is used
to calculate linear absorption coefficient, linear emission
coefficient and net gain. The barrier layer thickness is 20
nm while the thickness of the clad layer is 75 nm, see
Figure 2. All calculations are done at τin = 0.1 ps [3] and
carrier density 2 × 1024 m–3. Also we calculate the small
signal gain for structures contain one and six layers. Gain
coefficients are calculated using Equation (7) for several
values of input power.
Figure 3 shows a comparison between the linear ab-
sorption and emission coefficients where a multi-peaks
appear for ground and excited state transitions. One can
refers to the higher emission value compared to that of
absorption which results from lower transparency value
for this structure. The net gain is shown in Figure 4,
where a double peak can also be seen. This is very im-
portant in some applications. For example, this can be
used in long haul optical transmission. The reason for
this double emission is reasoned to finite ground state
relaxation time, which brings ground state emission to a
constant value after the excited state threshold [10]. Fig-
ure 5 shows the effect of intraband relaxation time τin
where a higher gain is obtained at longer intraband time.
Gain of the highest peak increases by ~ 4.5 time when τin
increases from 0.1 ps to 0.5 ps. Really, intraband relaxa-
tion time controlled the transition between intersubband
thus one can use this property to work with the same
structure at higher gain by choosing the subbands that
occur between them. Also, one can refers to the some-
what increase between the ground and excited peaks with
inraband relaxation time.
Rate equations are then solved at steady state, using
the parameters listed in Table 1, the QD-SOA character-
istics are examined. Small-signal gain spectrum of this
QD-SOA is shown in Figure 6. These gain values are
comparable to that obtained by Ben-Azra [9]. Note that it
is obtained here at a lower current value. So, this is a
good modification. The effect of QD layer is also exam-
ined where the gain increases with QD layers as shown
in Figure 7. Figure 8 shows the output power calculated
as a function of carrier density with input power is taken
as a parameter. Including the shot noise part, the noise
figure spectrum is shown in Figure 9, while the noise
figure curve at different carrier densities is shown in
Figure 10 from the last two figures one can refers to the
lower noise accompanied with this amplifier while the
last three figures shows the properties of ZnSe/ZnS
QD-SOA which is a good results to use it in applications.
Figure 2. QD system contain six active layers.
Figure 3. Comparison between linear absorption and emis-
sion coefficients.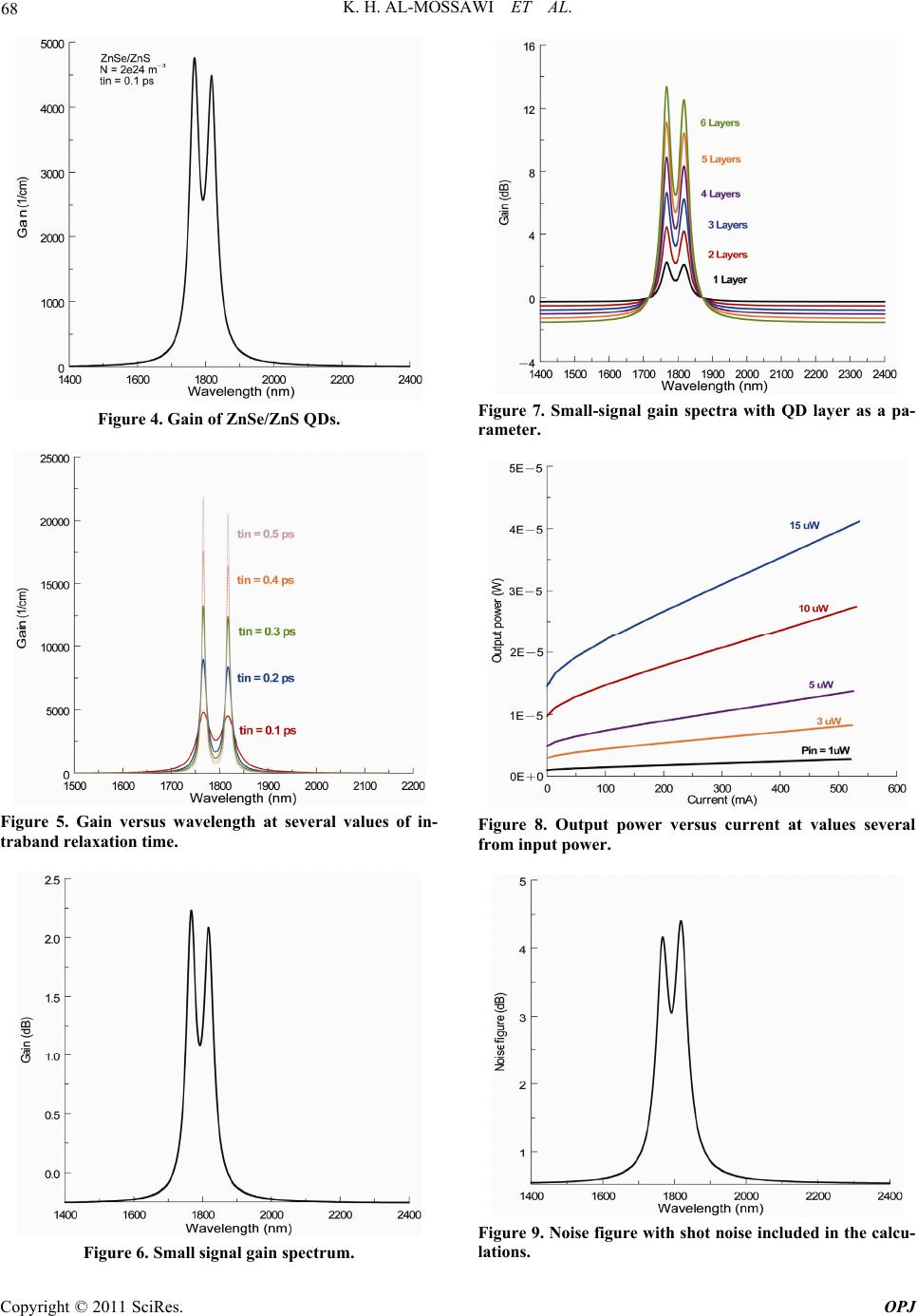

K. H. AL-MOSSAWI ET AL.
68
Figure 4. Gain of ZnSe/ZnS QDs.
Figure 5. Gain versus wavelength at several values of in-
traband relaxation time.
Figure 6. Small signal gain spectrum.
Figure 7. Small-signal gain spectra with QD layer as a pa-
rameter.
Figure 8. Output power versus current at values several
from input power.
Figure 9. Noise figure with shot noise included in the calcu-
lations.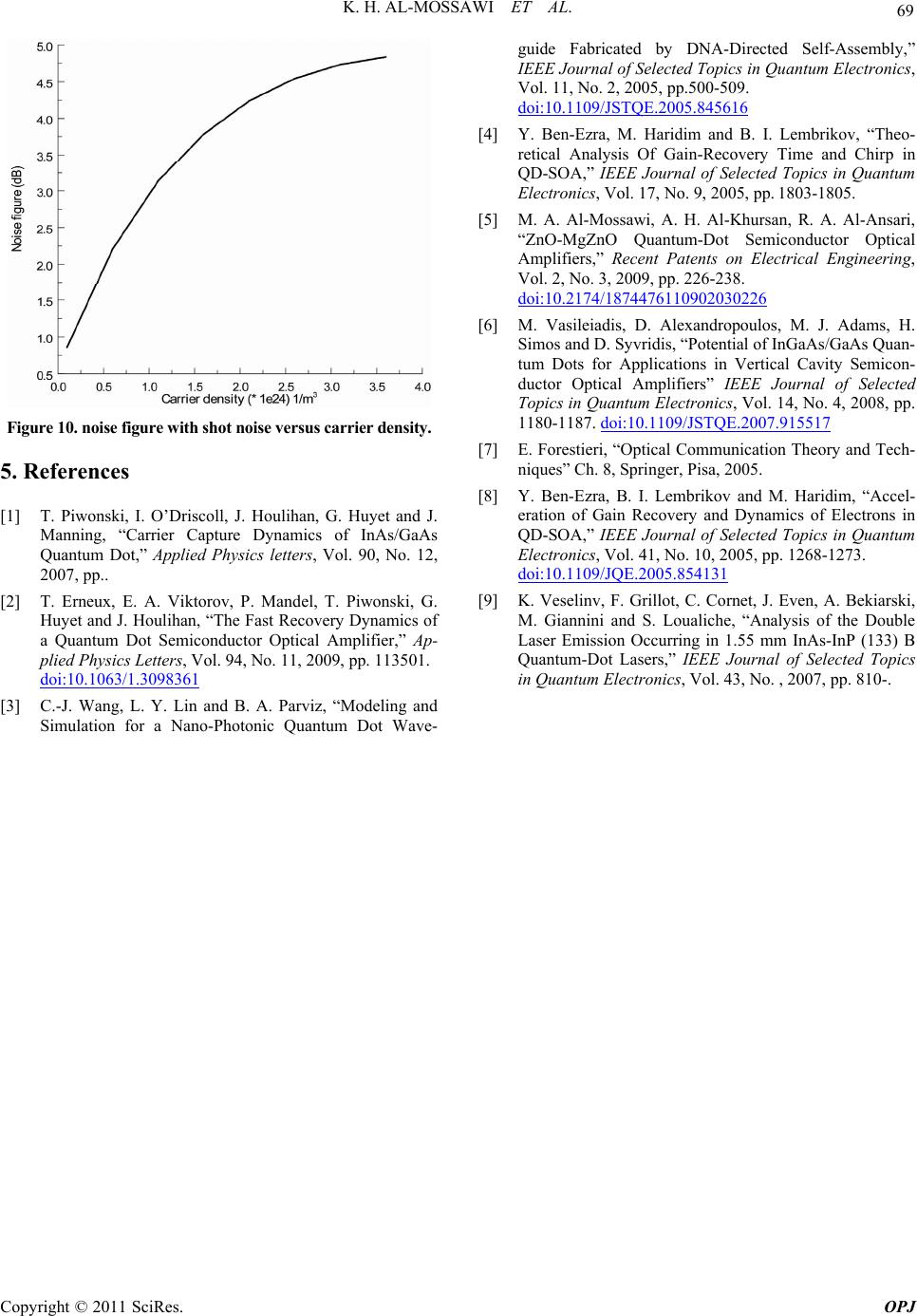

K. H. AL-MOSSAWI ET AL.
69
Figure 10. noise figure with shot noise versus carrier density.
5. References
[1] T. Piwonski, I. O’Driscoll, J. Houlihan, G. Huyet and J.
Manning, “Carrier Capture Dynamics of InAs/GaAs
Quantum Dot,” Applied Physics letters, Vol. 90, No. 12,
2007, pp..
[2] T. Erneux, E. A. Viktorov, P. Mandel, T. Piwonski, G.
Huyet and J. Houlihan, “The Fast Recovery Dynamics of
a Quantum Dot Semiconductor Optical Amplifier,” Ap-
plied Physics Letters, Vol. 94, No. 11, 2009, pp. 113501.
doi:10.1063/1.3098361
[3] C.-J. Wang, L. Y. Lin and B. A. Parviz, “Modeling and
Simulation for a Nano-Photonic Quantum Dot Wave-
guide Fabricated by DNA-Directed Self-Assembly,”
IEEE Journal of Selected Topics in Quantum Electronics,
Vol. 11, No. 2, 2005, pp.500-509.
doi:10.1109/JSTQE.2005.845616
[4] Y. Ben-Ezra, M. Haridim and B. I. Lembrikov, “Theo-
retical Analysis Of Gain-Recovery Time and Chirp in
QD-SOA,” IEEE Journal of Selected Topics in Quantum
Electronics, Vol. 17, No. 9, 2005, pp. 1803-1805.
[5] M. A. Al-Mossawi, A. H. Al-Khursan, R. A. Al-Ansari,
“ZnO-MgZnO Quantum-Dot Semiconductor Optical
Amplifiers,” Recent Patents on Electrical Engineering,
Vol. 2, No. 3, 2009, pp. 226-238.
doi:10.2174/1874476110902030226
[6] M. Vasileiadis, D. Alexandropoulos, M. J. Adams, H.
Simos and D. Syvridis, “Potential of InGaAs/GaAs Quan-
tum Dots for Applications in Vertical Cavity Semicon-
ductor Optical Amplifiers” IEEE Journal of Selected
Topics in Quantum Electronics, Vol. 14, No. 4, 2008, pp.
1180-1187. doi:10.1109/JSTQE.2007.915517
[7] E. Forestieri, “Optical Communication Theory and Tech-
niques” Ch. 8, Springer, Pisa, 2005.
[8] Y. Ben-Ezra, B. I. Lembrikov and M. Haridim, “Accel-
eration of Gain Recovery and Dynamics of Electrons in
QD-SOA,” IEEE Journal of Selected Topics in Quantum
Electronics, Vol. 41, No. 10, 2005, pp. 1268-1273.
doi:10.1109/JQE.2005.854131
[9] K. Veselinv, F. Grillot, C. Cornet, J. Even, A. Bekiarski,
M. Giannini and S. Loualiche, “Analysis of the Double
Laser Emission Occurring in 1.55 mm InAs-InP (133) B
Quantum-Dot Lasers,” IEEE Journal of Selected Topics
in Quantum Electronics, Vol. 43, No. , 2007, pp. 810-.