 World Journal of Nano Science and Enginee ring, 2011, 1, 37-44 doi:10.4236/wjnse.2011.12006 Published Online June 2011 (http://www.SciRP.o rg/journal/wjnse) Copyright © 2011 SciRes. WJNSE Vibration of Nano Beam Induced by Ramp Type Heating Hamdy M. Youssef1, Khaled A. Elsibai2 1Faculty of Engineering, Umm Al-Qura University, Makkah, Saudi Arabia 2Mathematic s De partment, Faculty Science, Umm Al-Qura University, Makkah, Saudi Arabia E-mail: {yousefanne, drkhaledelsibai}@yahoo.com Received March 23, 2011; revised April 18, 2011; accepted May 8, 2011 Abstract The non-Fourier effect in heat conduction and the coupling effect between temperature and strain rate, be- came the most significant effects in the nano -scale beam. In the present study, a generalized solution for the generalized thermoelastic vibration of a bounded nano-beam resonator induced by ramp type of heating is developed and the solutions take into account the above two effects. The Laplace transforms and direct me- thod are used to determine the lateral vibration, the temperature, the displacement, the stress and the energy of the beam. The effects of the relaxation time and the ramping time parameters have been studied with some comparisons. Keywords: Thermoelasticity, Nano-Beam, Ramp-Type Heating, Non-Fourier Heat Conduction 1. Introduction The generalized thermoelasticity theories have been de- veloped with the aim of removing the paradox of infinite speed of heat propagation inherent in the classical dy- namical coupled thermoelasticity theory (Biot-CTE) [1], Lord and Shulman (L-S) [2] obtained a wave-type heat equation by postulating a new law of heat conduction to replace the classical Fourier’s law. Since the heat equa- tion of this theory is of the wave-type, it automatically ensures finite speeds of propagation for heat and elastic waves. The remaining governing equations for this theory, namely, the equations of motion and constitutive relations, remain the same as those for the coupled theory. Many attempts have been made r ecently to investigate the elastic properties of nanostructured materials by ato- mistic simulations. Diao et al. [3] studied the effect of free surfaces on the structure and elastic properties of gold nanowires by atomistic simulations. Although the atomistic simu la tion is a good wa y to c a lc ulate the elastic constants of nanostructured materials, it is only applica- ble to homogeneous nanostructured materials (e.g., na- noplates, nanobeams, nanowires, etc.) with limited num- ber of atoms. More over, it is difficult to ob tain the elastic properties of the heterogeneous nanostructured materials using atomistic simulations. For these and other reasons, it is prudent to seek a more practical approa ch. One suc h approach would be to extend the classical theory of elas- ticity down to the nanosca le by including in it the hither- to neglected surface/interface effect. For this it is neces- sary first to cast the latter within the framework of con- tinuum elasticity. Nano-mechanical resonators have attracted considera- ble attention recently due to their many important tech- nological applications. Accurate analysis of various ef- fects on the characteristics of resonators, such as reso- nant frequencies and quality factors, is crucial for de- signing high-performance components. Many authors have studied the vibration and heat transfer process of beams. Kidawa [4] has studied the problem of transverse vibrations of a beam induced by a mobile heat source. The analytical solution to the problem was obtained us- ing the Green ’s functi ons met hod. H owever, Kidawa di d not consider the thermoelastic coupling effect. Boley [5] analyzed the vibrations of a simply supported rectangular beam subjected to a suddenly applied heat input distri- buted along its span. Manolis and Beskos [6] examined the thermally induced vibration of structures consisting of beams, exposed to rapid surface heating. They have also studied the effects of damping and axial loads on the structural response. Al-Huniti et al. [7] investigated the thermally induced displacements and stresses of a rod using the Laplace transformation technique. Ai Kah Soh et al. studied the vibration of micro/nanoscale beam re- sonators induced by ultra-short-pulsed laser by consider- ing the thermoel asti c coupling term i n [ 8,9]. When very fast phenomena and small structure di-  H. M. YOUSSEF ET AL. Copyright © 2011 SciRes. WJNSE mensions are involved, the classical law of Fourier be- comes inaccurate. A more sophisticated model is then needed to describe the thermal conduction mechanisms in a physically acceptable way. Modern technology has enabled the fabrication of materials and devices with characteristic dimensions of a few nanometers. Examples are super-lattices, na nowires, and quantum do ts. At these length scales, the familiar continuum Fo urie r law for heat conduction is expected to fail due to both classical and quantum size effects [10]. Among many applications, the stud yin g of t he t he rmoelastic damping in MEMS /NEM S has been improved in [11,13]. It is worthwhile to mention here that in most of the earlier studies, mechanical or thermal loading on the bounding surface is considered to be in the form of a shock. However, the sudden jump of the load is merely an idealized situation because it is impossible to realize a pulse described mathematically by a step function; even very rapid rise-time (of the order of 10–9 s) may be slo w in terms of the contin uum. This is partic ularly true in the case of second sound effects when the thermal relaxation times for typical metals are less than 10–9 s [14]. It is thus felt that a finite time of rise of external load (mechanical or thermal) applied on the surface should be considered while studying a practical problem of this nature. Most ultrafast heat sources (such as certain lasers) involve the emission of a pulse (for example) that heats a material over a finite time due to the finite rise time of the pulse. Considering the aspect of rise of time, Misra et al. [15] and Youssef with many authors investigated many ap- plications in which the ramp-type heating is used [16- 22]. In this paper, the non-Fouri er effe c t in hea t co nd uc ti o n, and the coupling effect between temperature and strain rate in nanoscale beam will be studied. In the present work, a generalized solution for the generalized ther- moelastic vibration of a nano beam resonator i nduced by ramp type of heating will be developed. The solution takes into account the above two effects. The Laplace transformation method will be used to determine the lat- eral vibration, the temperature, the displacement, the stress and the energy of the beam. The effects of the re- laxation time and the ramping time parameters will be studied and represented graphically. 2. Problem Formulation Since beams with rectangular cross-sections are easy to fabricate, such cross-sections are commonly adopted in the design of NEMS resonators. Consider small flexural deflections o f a th in elastic beam of length , width −≤≤ and thickness −≤≤ , for which the x, y and z axes are de- fined along the longitudinal, width and thickness direc- tions of the beam, respectively. In equilibrium, the beam is unstrained, unstressed, and at temperature T0 every- where [8]. In the present study, the usual Euler–Bernoulli as- sumption [8,9] is adopted, i.e., any plane cross-section, initially perpendicular to the axis of the beam, remains plane and perpendicular to the neutral surface during bending. Thus, the di s plac ements ar e given by ( )()( ) ,,0,,, ,, w xt uzvwxyztwxt x ∂ =−= = ∂ (1) Hence, the differential equation of thermally induced lateral vibration of the beam may be expressed in the form: 2 42 42 2 0 T T M w Aw EI xtx ρα ∂ ∂∂ ++ = ∂∂∂ , (2) where E is Young’s modulus, I [= bh3 /12] is the inertial moment about x-axis, is the density of the beam, is the coefficient of linear thermal expansion, the lateral deflection, x is the distance along the lengt h o f t he b eam, is the cross section area, t is the time, and is the thermal moment, which is de- fined as , (3) where 0 θ = − is the dynamical temperature incre- ment of the resonator, in which T(x, z, t) is the tempera- ture distribution and T0 is the environ mental temperature. The non-Fourier heat conduction equation has the fol- lowing form [16-18]: 22 20 22 2 o e t kk xz t υ θθ ∂∂∂ ∂ +=+ + ∂ ∂∂ ∂ , (4) where e =++ is the volumetric strain, where is the specific heat at constant volume, is the thermal relaxat ion ti me, k is t he t he r mal c onduc ti vi t y a nd in which is Po i s son’s ratio . Where there is no heat flow across the upper a nd lower surfaces of the beam, so that at , for a very thin beam and assuming that the temperature va- ries in terms of a function along the thickness direction, where , gives: ()()( ) 1 , ,,sinxz tx tpz θθ = .  H. M. YOUSSEF ET AL. Copyright © 2011 SciRes. WJNSE Hence, Equation ( 2) gives ( ) 2/2 42 1 42 32 /2 12 sind 0 h T h w Awzpz z EI xt hx αθ ρ − ∂ ∂∂ ++ = ∂∂ ∂ ∫ (5) and Equation (4) gives ( )( ) ( ) 22 11 2 22 0 1 22 sin sin sin o pz ppz x CT w pz z tk k tx υ θθ ρβ τθ ∂− ∂ ∂∂ ∂ =+− ∂∂∂ (6) After doing the integrations, Equation (5) takes the form 2 42 1 42 22 24 0 T w Aw EI xth x αθ ρ π ∂ ∂∂ ++ = ∂∂ ∂ . (7) In Equation (6), we multiply the both sides by z and integrating with respect to z from 2h− to 2h, then we obtain 2 2 20 1 π 24 o Thw p β θθτ ηθ ∂∂∂ ∂ −=+ − ∂ , (8) where . Now, for simplicity we will use the following non- dimensional variables: ()() ()( ) 2 2 1 1 , ,,,,,,, ,, oo oo o o xw hcxwhtct E c ET ητη τ θ σ σθ ρ ′ ′′′′ = = ′′ = == (9) The n, we have 2 42 1 12 42 2 0 ww AA xt x θ ∂ ∂∂ ++ = ∂∂∂ , (10) and 2 1311 4 ow t θθ τθ ∂∂∂ ∂ −=+ − ∂ ∂ ∂∂ , (11) where 2 2 12 34 22 24 12 ,,, 24 to Th AAApAk hh απβ η π === = , and we have canceled the prime for convenient. 3. Formulations the Problem in the Laplace Transform Domain Applying the Laplace transform for Equations (10) and (11) defined by the formula ()( )( ) 0 ed st fs Lftftt ∞− = = ∫ . Hence, we obtain the following system of differential equations 2 421 12 d d0 wAs wA θ , (12) and ( ) 22 2 1311 4 22 dd dd o w A ssA xx θθ τθ −=+− . (13) We have considered all the initial states of variables were zero, i.e. ( )()( )() 1 1 d,0d ,0 ,0,0 0 dd x wx x wx xx θ θ == == (14) We can re-write the above system of equations in the form 2 421 12 42 d d0 dd Asw A xx θ ++= , (15) and 11 2 w αθ α , (16) where ( )( ) 22 132 4 , oo AssssA ατα τ = ++=+ By el i mi nat in g from the above system of equation, we get ( ) 64 222 12 2111 0DADAs DAsw αα α −++ −= , (17) where satisfies the same equation, i.e. ( ) 64222 12 21111 0DADAs DAs ααα θ −++ −= . (18) The characteristic equation can be presented as (19) The roots of this equation, namely, 1 λ ±, 2 λ ± and 3 λ ±, satisfy the following rela tions , 22 22 222 1223 131 As m λλ λλ λλ , . We can consider the solution take the form , (20) and ( ) 6 11exp i = =∑, (21)  H. M. YOUSSEF ET AL. Copyright © 2011 SciRes. WJNSE where i C and i E (i = 1, 2, , 6) are some parame- ters d epend, only, on s. Using Equation (16) and (21), we get , this gi ves ( ) ( ) 2 6 122 11 exp iii ii Cx λ θα λ λα = = −− ∑ . (22) Now, to get the values of the constants i C and i E we will consider the two ends of the micro-beams are clamped, then the boundary conditions are [8,9]: ( )( ) 2 2 d, ,0 d w Lt w Ltx ± ±= = , (23) and loaded thermally by ramp-type hea ti ng, which give ( ) 0 0 0 for0 ,for 0 1 for t t Ltt t t tt θθ ≤ ± =<< ≥ , (24) where is non-negative constant and is called ramp- type parameter and 0 θ is co ns tant [18] . After using Laplace transform, the above conditions take the forms ( ) 2 2 d w Ls w Lsx ± ±= = , (25) and ( )( ) 0 0 12 0 1 ts e s Fs ts θ θ − − = = . (26) Applying the conditions (25) and (26) into Equations (20) and (22), we obtain , (27) , (28) ( ) ( ) ( ) 2 3 2 12 1 cosh iii ii Fs CL λλα λα = = − − ∑ . (29) By solving the above system of linear algebraically equations, we get The lateral deflection ( )( )() ( )( ) ( )() ( )( ) ( )() ( )( ) 112 2 2222 22222222 1213 12321323 cosh cosh cosh coshcoshcosh , xL xL wxs G λλ λλ λλλλ λλλλλλλλ = ++ −− −−−− (30) The tempe rature ()( ) ( )() ()( )( ) ( )() ()( )( ) ( )() ()( )( ) 22 111 222 22 222222222 111 21 3211 232 2 33 3 2 2222 31132 3 cosh coshcoshcosh , ,sin cosh cosh xL xL x z sGpz xL λλλ λλλ θα λαλλλλλαλλλλ λλ λ λαλλλλ =−+ −−− −−− + −−− , (31) The displacement ( )( )() ( )( ) ( )() ( )( ) ( )() ( )( ) 33 3 1 11222 222222222222 1213 12321323 sinh cosh sinh coshsinhcosh ,, xL xL ux z szG λλλ λ λλλλλ λλλλ λλλλλλλλ −− −−−− , (32) where ( ) ( )( )( ) 222 1112 13 12 Fs G αλαλαλ αα −−− = . 4. The Stress and the Strain Energy The stres s on the x-axis, according to Hooke’s law is ( ) ,, xx T u xztE x σ αθ ∂ = − ∂ , (33) By using the non-dimensional variables in (9), we ob- tain the stress in the form ( ) 0 ,, xx T u xzt T x σ αθ ∂ = − ∂. (34) After using Laplace transform, the above equation gives  H. M. YOUSSEF ET AL. Copyright © 2011 SciRes. WJNSE ( ) 0 ,, xx T u xzs T x σ αθ ∂ = − ∂ . (35) By using Equations (31) and (32) with equation (35), we get ( )( )() ( )( ) ( )() ( )( ) ( )() ( )( ) ( )( )() ()( )( ) ( )() ( ) 22 11 1222 2222 2222 12131232 2 33 3 2222 1323 111 222 02 222222 111213211 cosh coshcoshcosh ,, cosh cosh cosh coshcoshcosh sin xx T xL xL x z szG xL xL xL T Gpz λλ λλλλ σλλλλ λλλλ λλ λ λλλλ λλλ λλλ αα λαλλλλ λαλ −−−− + −− −−−− ( )( ) ( )() ()( )( ) 2 33 3 2 2222 31132 3 cosh cosh xL λλ λ λαλλλλ + −−− (36) The energy which is generated on the beam is given by 2 3 2 ,1 11 1 22 2 ij ijxx xxxx ij w We ez x σσσ = ∂ === −∂ ∑ , (37) or, we can write as follows: ( ) 2 11 2 1 2 xx w WzLL x σ −− ∂ = − ∂ , (38) where is the Laplace inverse trans- form. 5. Numerical Inversion of the Laplace Transform In order to determine the solutions in the time domain, the Riemann-sum approximation method is used to ob- tain the numerical results. In t his me t ho d , a n y function in Laplace domain can be inverted to the time domain as ( )( )() 1 1Re 1 2 tNn n e in ft ff tt κ π κκ = =+− + ∑ (39) where Re is the real part and i is imagi nary numb er unit. For faster convergence, numerous numerical experiments have shown that the value of satisfies the relation [23]. 6. Numerical Results and Discussion Now, we will consider a numerical example for which computatio nal results are given. For thi s purpose, Silico n is taken as the thermoelastic material for which we take the following values of the different physical constants [24]: , , , , , . The aspect ratios of the beam are fixed as and bh=, when h is varied, L and b change accor- dingl y wit h h. For the nanoscale beam, we will take the range of the beam length . The original time t and the ramping time parameter will be considered in the picoseconds and the relaxa- tion time 0 τ in the r ange . The figures were prepared by using the non-di men- sional variables which are defined in (9) for a wide range of beam length 2L when , 01.0 θ = 6zh= and . In Figures 1-5, we represented the lateral vibration, the temperature, the displacement, the stress and the energy of the beam at different values of the relaxation time when 00.0 τ = (Biot model) and 00.02 τ = (L-S model) and we have found that, the relaxation time has significant ef fects on all the studied fields. In the conte xt of L-S model, the relaxation time gives values of the lateral vibration, the temperature, the displacement, the stress and the ener gy les s than their va lue s in the c onte xt of Biot model which is very obvious in the peek points. We can say that, in the context of the generalized thermoelasticity the speed of the wave propagation of all the studied fields ar e finite and the damping of the strain ener gy increasing. In Figures 6-10, we represented the lateral vibration, the temperature, the displacement, the stress and the energy of the beam at different values of the ramping time parameter when , and in the c ontext 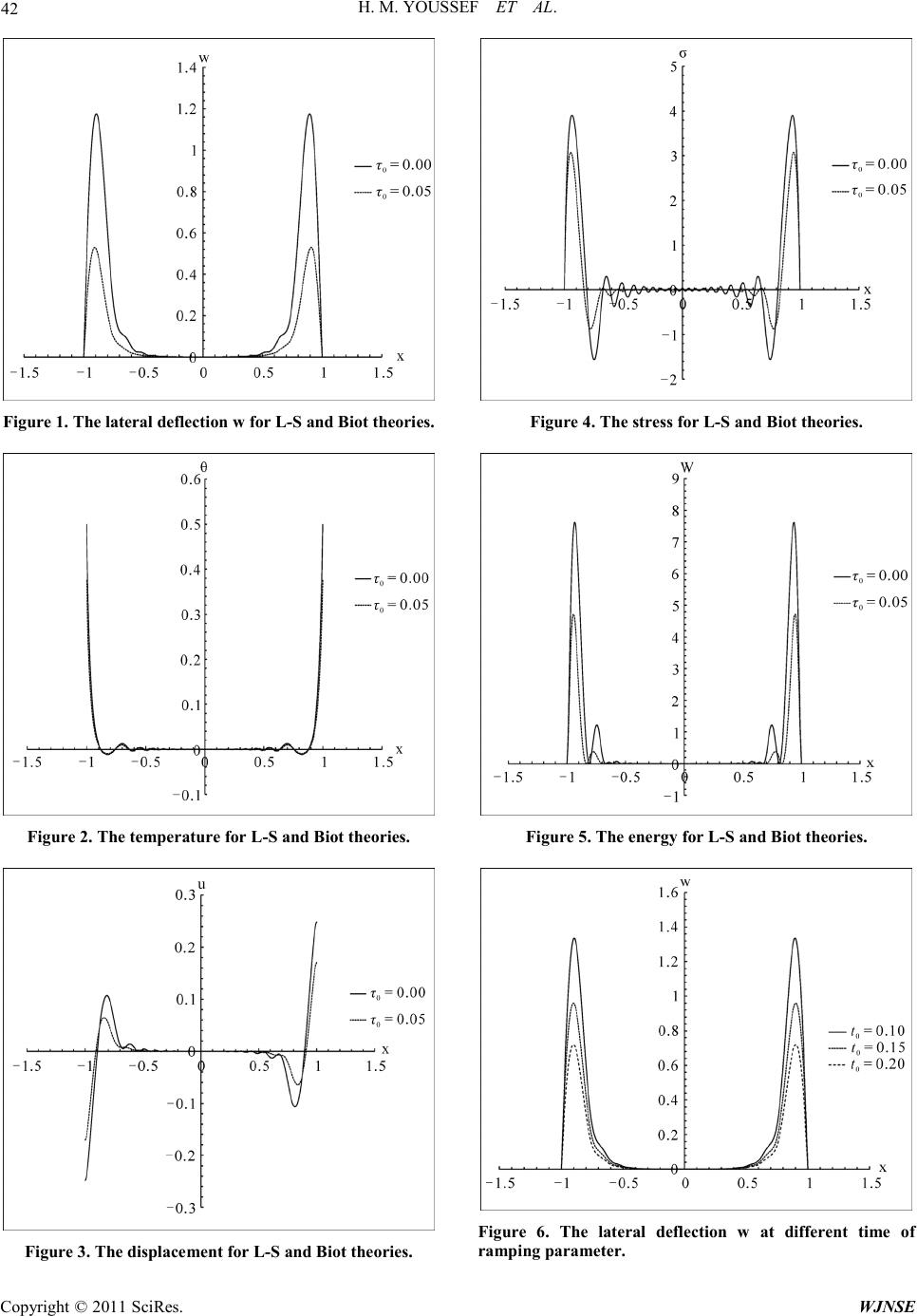 H. M. YOUSSEF ET AL. Copyright © 2011 SciRes. WJNSE Figure 1. The lateral deflection w for L-S and Biot theories. Figure 2. The temper at ure for L-S and Biot theories. Figure 3. The displacement for L-S and Biot theories. Figure 4. The stress for L-S and Biot theories. Figure 5. The energy for L-S and Biot theories. Figure 6. The lateral deflection w at different time of ramping par ameter.  H. M. YOUSSEF ET AL. Copyright © 2011 SciRes. WJNSE Figure 7. The temperature at different time of ramping parameter. Figur e 8. The displacement at different time of ramping parameter. Figure 9. The stress at different time of ramping parameter. Figure 10. The energy at different time of ramping para- meter. of L -S model. We have found that, the ramping time parameter has significant effects on all the studied fields. The increas- ing in the value of the ramping time parameter causes decreasing in the values of the lateral vibration, the tem- perature, the displacement, the stress and the energy which are very obvious in the peek points of the curves. Also , the da mping o f the st rain ene rgy is increases when the ramping time parameter increases. 7. Conclusions This paper has investigated the vibration characteristics of the deflection, the temperature, the displacement, the stress and the strain energy of an Euler–Bernoulli beam induced by a ramp type heating. An analytical direct method and numerical technique based on the Laplace transformation has been used to calculate the vibration of the deflection, the temperature, the displacement, the stress and the strain energy. The effects of the relaxation time and the ramping time parameter on all the studied fields have been shown and represented graphically. The non-Fourier law of heat conduction gives a finite speed of wave propagation and increases the damping of the strain ene rgy. 8. References [1] M. Biot, “Thermoelasticity and Irreversible Thermo- Dynamics,” Journal of Applied Physics, Vol. 27, No. , 1956, pp. 240-253. doi:10.1063/1.1722351 [2] H. Lord and Y. Shulman, “A Generalized Dynamical Theory of Thermoelasticity,” Journal of Mechanics and Physics of Solids, Vol. 15, No. 5, September 1967, pp. 299-309. doi:10.1016/0022-5096(67)90024-5  H. M. YOUSSEF ET AL. Copyright © 2011 SciRes. WJNSE [3] J. K. Diao, K. Gall and M. L. Dunn, “Atomistic Simula- tion of the Structure and Elastic Properties of Gold Na- nowires,” Journal of Mechanics and Physics of Solids, Vol. 52, No. 9, September 2004, pp.1935-1962. doi:10.1016/j.jmps.2004.03.009 [4] J. Kid awa-Kukla, “App lication of the Green Functions to the Problem of the Thermally Induced Vibration of a Beam,” Journal of Sound and Vibration, Vol. 262, No. 4, May 2003, pp. 865-876. doi:10.1016/S0022-460X(02)01133-1 [5] B. A. Boley, “Approximate Analyses of Thermally In- duced Vibrations of Beams and Plates,” Journal of Ap- plied Mechani cs , Vol. 39, No. 1, 197 2, pp. 212-216. doi:10.1115/1.3422615 [6] G. D. Manolis and D. E. Beskos, “Thermally Induced Vibrations of Beam Structures,” Computer Methods in Applied Mechanics and Engineering, Vol. 21, No. 3, March 1980, pp. 337-355. doi:10.1016/0045-7825(80)90101-2 [7] N. S. Al-Huniti, M. A. Al-Nimr and M. Naij, “Dynamic Response of a Rod Due to a Moving Heat Source under the Hyperbolic Heat Conduction Model,” Journal of Sound and Vibration, Vol. 242, No. 4, May 2001, pp. 629-640. doi:10.1006/jsvi.2000.3383 [8] A. K. Soh, Y. X. Sun and D. N. Fang, “V ibration of Mi- croscale Beam Induced by Laser Pulse,” Journal of Sound and Vibration, Vol. 311, No. 1-2, March 2 008, pp . 243-253. doi:10.1016/j.jsv.2007.09.002 [9] Y. X. Sun, D. N. Fang, M. Saka and A. K. Soh, “La- ser-Induced Vibrations of Micro-Beams under Different Boundary Conditions,” International Journal of Solids and Structures, Vol. 45, No. 7-8, April 2008, pp. 1993- 2013. doi:10.1016/j.ijsolstr.2007.11.006 [10] J. S. Rao, “Nonlinear Vibration and One Dimensional Stru ctures,” Advanced Theory of Vib ration, Wiley, New York, 199 2. [11] Y. X. Sun, D. N. Fang and A. K. Soh, “Thermoelastic Damping in Micro-Beam Resonators,” International Journal of Solids and Structures, Vol. 43, No. 10, May 2006, pp . 3213-3229. doi:10.1016/j.ijsolstr.2005.08.011 [12] D. N. Fang, Y. X. Sun and A. K. Soh, “Analysis of Fre- quency Spectrum of Laser-Induced Vibration of Micro- beam Resonators,” Chinese Physics Letters, Vol. 23, No. 6, 2006, pp. 1554-15 57. [13] A. Duwel, J. Gorman, M. Weinstein, J. Borenstein and P. Ward, “Exp eri mental Study of Ther moelasti c Da mping in MEMS Gyros,” Sensors and Actuators A, Vol. 103, No. 1-2, January 2003, pp. 70-75. doi:10.1016/S0924-4247(02)00318-7 [14] J. C. Misra, S. C. Samanta, A. K. Chakrabarti and S. C. Misra, “Magnetothermoelastic Interaction in an Infinite Elastic Continuum with a Cylindrical Hole Subjected to Ramp-Type Heating”, International Journal of Engi- neering Science, Vol. 29, No. 12, 1991, pp. 1505-1514. doi:10.1016/0020-7225(91)90122-J [15] J. C. Misra, S. C. Samanta and A. K. Chakrabarti, “M ag- netothermoelastic Interaction in an Aeolotropic Solid Cy- linder Subjected to a Ramp-T ype Heating”, In ternational Journal of Engineering Science, Vol. 29, No. 9, 1991, pp. 1065-1075. doi:10.1016/0020-7225(91)90112-G [16] H. M. Youssef, “State-Space on Generalized Thermoe- lasticity for an Infinite Material with a Spherical Cavity and Variable Thermal conductivity Subjected to Ramp- Type Heating,” Journal of CAMQ, Applied Mathematics Institute, Vol. 13, No. 4, 20 05, pp. 369-390. [17] H. M. Youssef, “Problem of Generalized Thermoelastic Infinite Medium with Cylindrical Cavity Subjected to a Ramp-Type Heating and Loading,” Journal of Archive of Applied Mechanics, Vol. 75, No. , 2006, pp. 553-56 5. doi:10.1007/s00419-005-0440-3 [18] H. M. Youssef, “Two-Dimensional Generalized Ther- moelasticity Problem for a Half-Space Subjected to Ramp-Type Heating,” European Journal of Mechanics- A/Solids, Vol. 25, No. 5, September-October 2006, pp. 745-763. doi:10.1016/j.euromechsol.2005.11.005 [19] H. M. Youssef and A. H. Al-Harby, “State-Space Ap- proach of Two-Temperature Generalized Thermoelastic- ity of Infinite Body with a Spherical Cavity Subjected to Differen t Types of Ther mal Loadi ng,” Journal of Archive of Applied Mechanics, Vol. 77, No. 9, 2007, pp. 675-687. doi:10.1007/s00419-007-0120-6 [20] H. M. Youssef, “Two-Dimensional Problem of Two- Temperatu re Generalized Thermoelastic Half-Space S ub- jected t o Ramp-Type Heating,” Journal of Computational Mathematics and Modeling, Vol.19, No. 2, 2008, pp. 201-235. doi:10.1007/s10598-008-0014-7 [21] M. A. Ezzat an d H. M. Youssef, “S tat-S pace Approach of Conducting Magneto-Thermoelastic Medium With Vari- able Thermal Conductivity Subjected To Ramp-Type Heating,” Journal of Thermal Stresses, Vol. 32, No. , 2009, pp . 414-427. doi:10.1080/01495730802637233 [22] H. M. Youssef and A.A. El-Bary, “Generalized Ther- moelastic Infinite Layer Subjected to Ramp-Type Ther- mal and Mechanical Loading under Three Theories-State Space Approach,” Journal of Thermal Stresses, Vol. 32, No. , 2009, pp. 1-18. [23] D. Tzou, “Macro-to-micro heat transfer,” Ta ylor & F ran- cis, Washington DC, 1996. [24] R. Hull, “Properties of Silicon, INSPEC,” The Institution of Electrical Engineers, London, New York, 1988.
|