World Journal of Nano Science and Engineering, 2011, 1, 21-26
doi:10.4236/wjnse.2011.1 2004 Published Online June 2011 (http://www.SciRP.org/journal/wjnse)
Modelling of Internal Stresses in Sheet Glass during the
Cooling
Saci Benbahouche1, Fouad Roumili1, Jean-Christophe Sangleboeuf2
1Laboratory of Applied Precision Mechanics, Optics and Precision Mechanical Institute,
Ferhat Abbas University, Setif, Algeria
2Laboratoire de Mécanique appliqué de l’Université de Rennes, Campus de Beaulieu,
Rennes cedex, France
Received February 23, 2011; revised March 14, 2011; accepted April 7, 2011
Abstract
Internal stresses in glass are generated by interactions between thermal contraction, elasticity at low tem-
peratures, viscoelastic flow at higher temperature, and temperature gradients caused by cooling. This work
intends to work out calculation program for real temperature distribution and internals stress, and to study
their behaviour during the quenching through a flat plate of soda-lime glass from different temperatures.
Keywords: Modelling, Internal Stresses, Glass
1. Introduction
The internal stresses in the glass are tensions which can
be transient during the thermal treatment or the perma-
nent tensions after the treatment and that are important of
the practical view point.
In thi s sense, t he t heo r y wa s n o t d e vel op e d a lo ng t i me,
the first theoretical work in this sense has been done by
Adams and Williamson [1], carrying on the analytic cal-
culation of the distribution of the temperature during the
cooling of the glass. After several years, models of
visco-elastics pro perties o f the glass b egan to appear, but
the functional method of calculation takes in considera-
tion the thermoplastic stress formation and at the same
time their relaxation by the viscous out-flow that could
be made since the apparition of the computer. The first
work t hat c arr ies o n t he nu me ric t ransi ent and per mane nt
internal stress calculation in the glass been published by
Lee, Roger and Woo [2]; at the following of several
works of research done, and on the basis of these works
we present this ar tic le .
2. Fundamental Equations
2.1. General Considerations
In all the following theory, which is developed for a flat
plate in glass, it is supposed that the lateral dimensions
are superior to the thickness of where the normal con-
straints in full surface tend everywhere toward zero; by
these conditions, the thermal stresses become stresses
hover and u niforms in t he plan y-z, but only with x [2-6].
(,)
yz xt
σσσ = = (2.1.1)
0
x
σ = (2.1.2)
where, x, y, z are the principal axes; t is the parameter
time .
2.2. Equation of the Deformation
The Equation (2.2.1) generally describes all deformation
of an infinite plate of which the initial temperature T0 at
the instant t = 0 change to the temperature T(x, t) and at
the fictive temperature Tf (x, t); this defor mation is called
free deformation and which given by the following rela-
tion [2-4,7]:
( )( )
( )
( )
00
,, ,
thgl g f
xtTxt TTxt T ε ααα

= −+−− 
 
(2.2.1)
where, α
g,
α
l: are respectively coefficients of thermal
expansion in the glass state and coefficients of thermal
expansion in the liquid state in thermodynamic equilib-
rium; T(x, t): Temperature in the x point and at the in-
stant really determined t; Tf (x, t): fictive temperature in
the x point and at the instant t; T(x, 0) = T0: the initial

S. BENBAHOUCHE ET AL.
22
temperature at the instant t = 0.
We suppos es at the inst ant t = 0 a stabilised state, then:
Tf (x, 0) = T0.
From the conditions cited before, the plate doesn’t
change in the plan y-z, but independently of x, the ge-
ometry of the glass plate and the continuity of material
the lengthy of the plate determines the real deformation
which only depends of the time [2,3,6,7]:
()( )()
,xttf x εε = ≠
(2.2.2)
2.3. Stress Equations
In the interval of transition, two simultaneous effects
produce, the first is the generation of stresses which is
caused by the interaction between the thermal contrac-
tion (elasticity) for the low temperatures and the visco-
elasticity that increase for the elevated temperatures,
then the second effect that is the relaxation of these
stresses.
The stress is generated by the difference between the
free deformation and the real deformation [2-4,7]:
( )( )()
,,
1
g th
E
xtt xt σ εε
µ
= −


−
(2.3.1)
where, σ
g(x, t): Stress generated in the x point and at the
instant t; E: YOUNG modulus: μ POISSON Coeffi-
cient.
But for the glass in the state material visco-elastic, the
equation of stress is expressed such as being the sum of
stress generated variations with regard to the time t while
considering the relaxation of these stresses that also de-
pends of cooling time, and this equation is called visco-
elastic equation whic h is gi ven by [2-5,7] :
( )()( )
0
,
,d
tg
xt
xtRttt
t
σ
σ
′ ∂
′′ = −′
∂
∫
(2.3.2)
where, R: Stress relaxatio n modulus.
With the relation of equilibrium which is defined as
being the sum of the internal stresses the lengthy of the
half of the plate thickness (at the rate of symmetry) must
be equal to z e ro; this relation is calle d basis equatio n:
( )
0
,d 0
l
xt x σ =
∫
(2.3.3)
2.4. Fictive Temperature
Tool [8] defines the fictive temperature Tf as being a
present temperature of an equilibrium state which corre-
sponds to give the state no eq uilibriu m, else sa id , it is the
proper temperature to the structure, it takes its residual
value just as the relaxation eliminates itself. It is a func-
tion of the position x and the time t, which is given by
the followin g eq uation [7,9,10]:
( )( )( )( )
0
,,, ,d
t
f
T
TxtT xtMxtxtt
t
ξξ
∂
′′ =−−


′
∂
∫
(2.4.1)
where M: structure relaxation Modulus; ξ: Reduced
time.
The reduced time ξ is defines by Lee and Roger [11]
as being the measured time at the low temperatures. With
the superposition of the time and the temperature of
which call simplicity thermo-rheological while using the
shift function Φ, from which comes the notion of the
reduced time.
The reduced time is in relation with the real time and
the s hift functio n Φ under the following form [3,9,12]:
( )()()
0
,,,, d
t
f
xtTxtTxtt ξ ′′ 
=Φ 
∫
(2.4.2)
However, ξ is obtained from the real time t, which
carries the shift functio n Φ to depend of Tf and as well o f
T, which is formulated by the following relation [7,12]:
( )
112
,2
fg fd
H
T TExpRTT T ξ


= −+−
 




(2.4.3)
where H: Activation energy; Rg: Gas Constant; Td:
Minimum annealing temperature.
From Rekhson and Mazurins [1 3] results, the s truc tur e
relaxation Modulus can be presented by the following
expression:
( )
0,68
v
MExp t
ξ
ξ

= −


(2.4.4)
where tv: Time of volume relaxation.
2.5. Stress Relaxation Modulus
Stress relaxation modulus R is calculated on the basis of
E and G respectively elasticity modulus and sliding
modulus which also depend of a time, and which given
by the following equation of int egral [2,7,11,14-16]:
()( )( )
0
42
3
R
GdR G
k
ξ
ξξξ ξξ
ξ
′
∂
′ ′′
− +=
′
∂
∫
(2.5.1)
where k: volume module which is in relation with a
YOUNG modulus E, the sliding modulus G and a
POISSON coefficient µ :
( )
12
2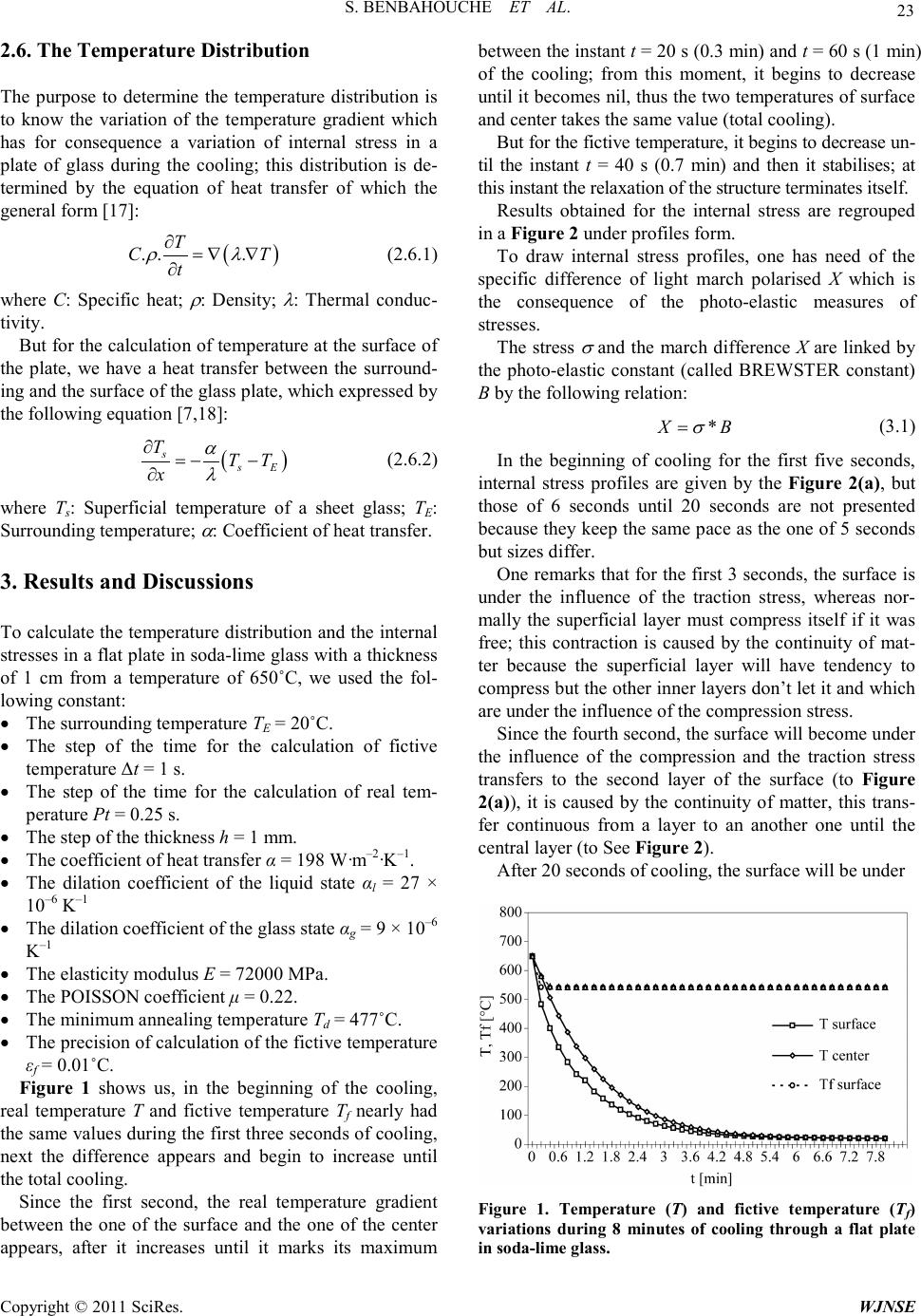1 3 EG
k
µ
µ
−
=+=
(2.5.2)

S. BENBAHOUCHE ET AL.
23
2.6. The Temperature Distribution
The purpose to determine the temperature distribution is
to know the variation of the temperature gradient which
has for consequence a variation of internal stress in a
plate of glass during the cooling; this distribution is de-
termined by the equation of heat transfer of which the
general form [17]:
( )
.. .
T
CT
t
ρλ
∂=∇∇
∂
(2.6.1)
where C: Specific heat;
ρ : Density; λ : Thermal conduc-
tivity.
But for the calculation of temperature at the surface of
the plate, we have a heat transfer between the surround-
ing and t he surface o f the gl as s p l ate , whic h exp re ssed b y
the followin g equation [7,18]:
( )
ssE
TTT
x
α
λ
∂=−−
∂
(2.6.2)
where Ts: Superficial temperature of a sheet glass; TE:
Surrounding temperature; α : Coefficient of heat transfer.
3. Results and Discussions
To calculate the temperature distribution and the internal
stresses in a flat plate in soda -lime gla ss wit h a thic kness
of 1 cm from a temperature of 650˚C, we used the fol-
lowing co nstant:
• The s urrounding temperature TE = 20˚C.
• The step of the time for the calculation of fictive
temperature Δt = 1 s.
• The step of the time for the calculation of real tem-
perature Pt = 0.25 s.
• The s tep o f t he thic kness h = 1 mm.
• The coefficient of heat transfer α = 198 W·m–2·K–1.
• The dilation coefficient of the liquid state αl = 27 ×
10–6 K–1
• The dilation coefficient of the glass state αg = 9 × 10–6
K–1
• The elasticity modulus E = 72000 MPa.
• The POISSON coefficient μ = 0.22.
• The mi nimum annealing temperature Td = 477˚C.
• The precision of calculation of the fictive temperature
εf = 0.01˚C.
Figure 1 shows us, in the beginning of the cooling,
real temperature T and fictive temperature Tf nearly had
the s ame val ues d uri ng the f irst t hre e sec ond s o f co olin g,
next the difference appears and begin to increase until
the total cooling.
Since the first second, the real temperature gradient
between the one of the surface and the one of the center
appears, after it increases until it marks its maximum
between the insta nt t = 20 s (0.3 min) and t = 60 s (1 min)
of the cooling; from this moment, it begins to decrease
until it beco mes nil, thus the two temperat ures of surface
and center takes the same value (total cooling).
But for the fic tive temp erature, it begin s to decrea se un-
til the instant t = 40 s (0.7 min) and then it stabilises; at
this instant the relaxation of the structure terminates itself.
Results obtained for the internal stress are regrouped
in a Figure 2 under profiles form.
To draw internal stress profiles, one has need of the
specific difference of light march polarised X which is
the consequence of the photo-elastic measures of
stresses.
The stress
σ and the march difference X are linked by
the photo-elastic constant (called BREWSTER constant)
B by the following rela tion:
*XB σ =
(3.1)
In the beginning of cooling for the first five seconds,
internal stress profiles are given by the Figure 2(a), but
those of 6 seconds until 20 seconds are not presented
because they keep the same pace as the one of 5 seconds
but sizes differ.
One remarks that for the first 3 seconds, the surface is
under the influence of the traction stress, whereas nor-
mally the superficial layer must compress itself if it was
free; this contraction is caused by the continuity of mat-
ter because the superficial layer will have tendency to
compress but the other inner layers don’t let it and which
are under the influence of the compres sio n str ess.
Since the fourth second, the surface will become under
the influence of the compression and the traction stress
transfers to the second layer of the surface (to Figure
2(a)), it is caused by the continuity of matter, this trans-
fer continuous from a layer to an another one until the
central layer (to See Figure 2).
After 20 seconds of cooling, the surface will be under
Figure 1. Temperature (T) and fictive temperature (Tf)
variations during 8 minutes of cooling through a flat plate
in soda-lime glass.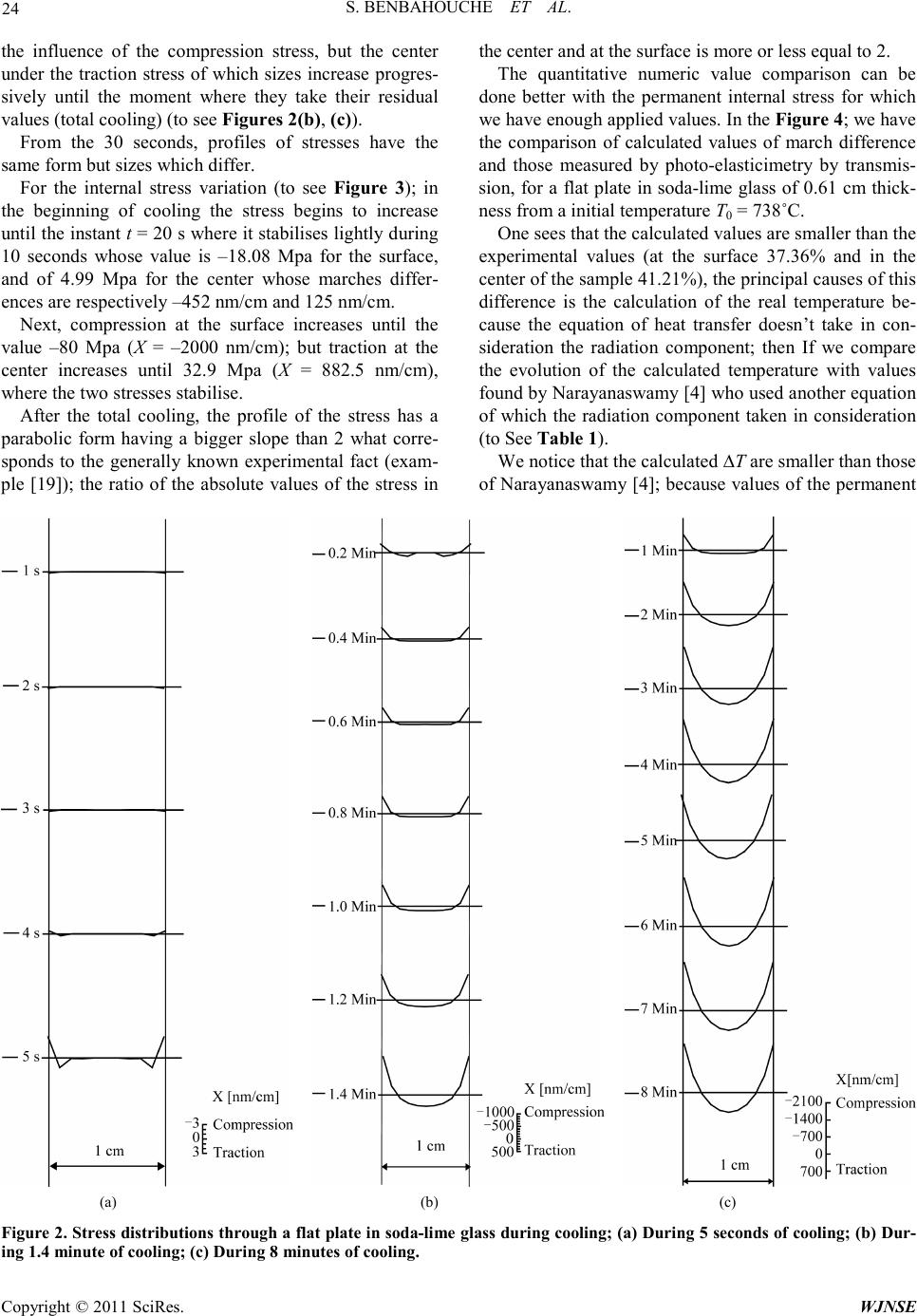

S. BENBAHOUCHE ET AL.
24
the influence of the compression stress, but the center
under the traction stress of which sizes increase progres-
sively until the moment where they take their residual
values (total cooling) (to see Figures 2(b), (c)).
From the 30 seconds, profiles of stresses have the
same form but sizes which differ.
For the internal stress variation (to see Figure 3); in
the beginning of cooling the stress begins to increase
until the i nstant t = 20 s wher e it stabilises lightly during
10 seconds whose value is –18.08 Mpa for the surface,
and of 4.99 Mpa for the center whose marches differ-
ences are respectively –452 nm/cm and 125 nm/ cm .
Next, compression at the surface increases until the
value –80 Mpa (X = –2000 nm/cm); but traction at the
center increases until 32.9 Mpa (X = 882.5 nm/cm),
where the two stresses stabilise.
After the total cooling, the profile of the stress has a
parabolic form having a bigger slope than 2 what corre-
sponds to the generally known experimental fact (exam-
ple [19]); the ratio of the absolute values of the stress in
the center and at the surface is more or less equal to 2.
The quantitative numeric value comparison can be
done better with the permanent internal stress for which
we have eno u g h ap p li ed val ues . I n the Figure 4; we ha ve
the comparison of calculated values of march difference
and those measured by photo-elasticimetry by transmis-
sion, for a flat plate in soda-lime glass of 0.61 cm thick-
ness from a initial temperature T0 = 738˚C.
One sees that the calculated values are smaller than the
experimental values (at the surface 37.36% and in the
center of the sample 41.21%), the principal causes of this
difference is the calculation of the real temperature be-
cause the equation of heat transfer doesn’t take in con-
sideration the radiation component; then If we compare
the evolution of the calculated temperature with values
found by Narayanaswamy [4] who used another equation
of which the radiation component taken in consideration
(to See Table 1).
We notice that the calculated ∆T are smaller than those
of Narayanaswamy [4]; because values of the permanent
(a) (b) (c)
Figure 2. Stres s distri butio ns th rough a f lat plat e in sod a-lime glass during cooling ; (a) Duri ng 5 sec onds of cooli ng; (b) Dur-
ing 1.4 minute of cooli ng; (c) Duri ng 8 minutes of cooling.

S. BENBAHOUCHE ET AL.
25
Table 1. The difference of temperature between the surface a nd the center ∆T during the c ooling of a flat plate in s oda-lime
glas s of 7.3 mm thickness from T0 = 67 7˚C.
t [s] 4 6 8 10 12 14 16
∆ T [˚C] Cal culat ed 83 84 86 86 87 87 86
Naray [4] 137 152 162 161 157 152 150
Figure 3. Internal stress variation during 8 minute of cool-
ing through a fl a t plate in sode-lime glass.
Figure 4. Comparison between calculated and measured
march differences for a flat plate in soda-lime glass of
thickness e = 0.61 cm.
internal stress are influenced in the first by the value of
the temperature gradient creates during the cooling;
therefore it is obvious that values of the permanent in-
ternal stress tha t we calculated must be smaller.
4. Conclusions
The numeric calculation method of the internal stress in a
flat plate in soda-lime glass, its cooling has been devel-
oped on the basis of knowledge of the distribution of the
calculated real temperature by Equations (2.6.1) and
(2.6.2); the reduced time and the distribution of the fic-
tive temperature by iteration method with Equations
(2.4.1), (2.4.2) and (2.4.3); the normalised relaxation
modulus of stress which is used then with the reduced
time, the real and fictive temperature to calculate the
internal stress by Equations (2.3.1), (2.3.2) and (2.3.3).
For the precision satisfying of the internal stress val-
ues, it is sufficient to calculate the normalised relaxation
modulus of a stress with a step of the time logarithmic
D = 0.25; for the calculation of a stress we have to our
disposition 35 values of this module.
During the calculation of the fictive temperature with
the precision 0.01˚C, it is sufficient to calculate the inte-
gral of the Equation (2.4.1) with the precision 0.1; the suf-
ficient time ste p in the prin cipal prog ram is one s e cond .
The calculation program proposed gives the evolution
of the temporary and permanent internal stress whose
concept is qualitatively exact; but quantitatively, the
comparison shows that values of the calculated internal
stress are smaller than the applied values, the main rea-
son of this difference is the insufficiency of the real
temperature (deficiency of the radiation component),
what has for consequence the obtaining of a small tem-
perature gradient so the internal stress.
5. Referen ces
[1] L. H. Adams and E. D. Williamson, “Annealing of
Glass,” Journal of the Franklin Institute, Vol. 190, No. 5,
1920, pp. 597-631.
[2] E. H. Lee, T. G. Rogers and T. C. Woo, “Residual
Stresses in a Glass Plate Cooled Symmetrically from
Both Surfaces,” Journal of the American Ceramic Society,
Vol. 48, No. 9, 1965, pp. 480-487.
doi:10.1111/j.1151-2916.1965.tb14805.x
[3] O. S. Narayanaswamy and R. Gardon, “Calculation of
Residual Stress in Glass,” Journal of the American Ce-
ramic Society, Vol. 52, No. 10, 1969, pp. 554-558.
doi:10.1111/j.1151-2916.1969.tb09163.x
[4] O.S. Narayanaswamy, “Stress and Structural Relaxation
in Tempering Glass,” Journal of the American Ceramic
Soci ety, Vol. 61, No. 3-4, 1978, pp. 146-152.
doi:10.1111/j.1151-2916.1978.tb09259.x
[5] D. R. Uhlmann and N. J. Kreidel, “Te mpering o f Glass,”
Glass Science and Technology, Vol. 5, Chapter 5, 1980,
pp. 145-213.
[6] H. S. Carslav and J. C. Jaeger, “Conduction of Heat in

S. BENBAHOUCHE ET AL.
26
Solids,” Ox ford University Press, Oxford, 1947, pp. 154-
165.
[7] J. Kavka, “Calcul de la Déformation et de Contrainte
Interne Durant la Première Phase de Refroidissement,”
Thèse de Doctorat, Institut d’Etat de Recherche verrière,
Hradec Kralove, République Tchèque, 1980.
[8] A. Q. Tool, “Relation between Inelastic Deformability
and Thermal Expansion of Glass in Ets Annealing
Range,” Journal of the American Ceramic Society, Vol.
29, No. 9, 1946 , p p. 24 0-253.
doi:10.1111/j.1151-2916.1946.tb11592.x
[9] R. Gardon and O. S. Narayanaswamy, “Stress and Vol-
ume Relaxation in the Annealing of Flat Glass,” Journal
of the American Ceramic Society, Vol. 53, No. 7, 1970,
pp. 380-385. doi:10.1111/j.1151-2916.1970.tb12137.x
[10] S. M. Ohlberg and T. C. Woo, “Thermal Stress Analysis
of Glass with Dependent Coefficient of Expansion,”
P.P.G. Industries Inc., University Pittsburg, P e nn syl van y,
1972.
[11] E. H. Lee and T. G. Rogers, “Non-Linear Effects of
Temperature Variation in Stress Analysis o Isothermally
Liear Visco-Elastic Materials,” Proceedings of IUTAM
Symposium on Second-Order, Pergamon Press, Haifa,
1964.
[12] O. S. Narayanaswamy, “A Model of Structural Relaxa-
tion in Glass,” Journal of the American Ceramic Society,
Vol. 54, No. 10, 1971, pp. 491-498.
doi:10.1111/j.1151-2916.1971.tb12186.x
[13] S. M. R ekhson an d O. V. Mazu rin, “Stress an d Structural
Relaxation in Na2O-CaO-SiO2 Glass,” Journal of the
American Ceramic Society, Vol. 57, No. 7, 1974, pp.
327-328. doi:10.1111/j.1151-2916.1974.tb10912.x
[14] E. H. Lee and T. G. Rogers, “Solution of Visco-Elastic
Stress Analysis Problems Using Measured Creep or Re-
laxation Function,” Journal of Applied Mechanics, Vol.
30, No. 3, 1963, p p. 127-133.
[15] R. Muki and E. Sternberg, “Transient Thermal Stress in
Visco-Elastic Materrials with Temperature Dependent
Properties,” Journal of Applied Mechanics, Vol. 28, No.
2, 1961, pp. 193- 207.
[16] G. W. Sch erer and S. M. Rekhson, “Voisco elastic – Elas-
tic Composites: I, General Theory,” Journal of the Ameri-
can Ceramic Society, Vol. 65, No. 7, 1982 , pp. 35 2-360.
doi:10.1111/j.1151-2916.1982.tb10470.x
[17] N. Piskounov, “Calcul Différentiel et Intégral，“ Tome II,
Editions MIR (traduit du Russe en Francçais), Moscou,
Russie, 1976.
[18] F. Beran ek, “Temperature distribution in Glass products,”
Informativni Prehed, Vol. 19, No. 4, H. Kralove, Cesky
Republic, 1976, pp. 17-29.
[19] M. Goldstein and M. Nakonecznyj, “Volume Relaxation
in Zinc Chloride Glass,” Physics and Chemistry of
Glasses, Vol. 6, No. 4, 1965, pp . 126-133.