Paper Menu >>
Journal Menu >>
 Open Journal of Safety Science and Technology, 2011, 1, 19 -29 doi:10.4236/ojsst.2011.11003 Published Online June 2011 (http://www.SciRP.org/journal/ojsst) Copyright © 2011 SciRes. OJSST Heinrich’s Fourth Dimension Robert Collins UT School of Public Health, Houston, USA E-mail: buckibooster@yahoo.com Received May 6, 2011; revised May 25, 2011; accepted June 5, 2011 Abstract In this article, the author uses accident data readily available from the United States Bureau of Labor Statis- tics to create a New Incident Pyramid, a modern day equivalent of Heinrich’s Triangle. This historical data is then combined with generally accepted statistical methods to show that the relationship between incident types first envisioned by Herbert William Heinrich in 1931 has a fourth dimension, time. Using statistical analysis methods derived from both a Binomial distribution and a Poisson distribution, this analysis will show how information derived from these accident summaries can be used to predict potential future events. The obvious conclusion reinforced by this analysis will be that the future date for potentially fatal accidents can only be delayed by focusing on accident prevention strategies that address all incidents without regard for the type of resulting injury. This analysis can be used by safety professionals to predict potential future outcomes for their establishments which can then be used to better communicate the need for improvements in accident prevention programs. Keywords: Heinrich’s Triangle, Heinrich’s Pyramid, New Incident Pyramid, OSHA Recordable Incidents, Lost Workday Cases, Fatalities, Fatal Accidents 1. Introduction In 1931, Herbert William Heinrich, one of the founding fathers of industrial safety and accident prevention, pub- lished the results of a study he performed while working for Traveler’s Insurance [1]. His original work revealed that, for every “major injury” resulting from a single accident, there were 29 “minor injuries” resulting from accidents and 300 no-injury accidents. The figure he produced, depicting these ratios, came to be known as Heinrich’s Triangle. The development of Heinrich’s Triangle followed a study of over 5000 cases. Ultima- tely, the injuries resulting from these cases were catego- rized as follows: Major Injuries: “Any case that is reported to insu- rance carriers or to the state compensation commis- sioner.” These would be equal to what OSHA (i.e., Occupational Safety and Health Administration) now defines as a recordable incident case. Minor Injuries: “A scratch, bruise, or laceration such as is commonly termed a first-aid case.” No-Injury Accidents: “An unplanned event involving the movement of a person or an object, ray, or sub- stance (slip, fall, flying object, inhalation, etc.), hav- ing the probability of causing personal injury or prop- erty damage.” Heinrich’s Triangle became the foundation on which many of today’s industrial accident prevention programs are built. Perhaps the most important lesson learned from this foundational work is that the path that leads to the prevention of accidents resulting in major injuries lies in investigating all accidents, including “No-Injury Acci- dents.” In a recent article [2], this author showed how the re- lationships among incident types first envisioned by H. W. Heinrich still has relevance today. This was accom- plished by updating Heinrich’s original triangle using BLS (United States Bureau of Labor Statistics) data from a recent 18-year period (1992-2008) to produce a New Incident Pyramid. This data is summarized in Table 1. This analysis showed that for each fatal work-related accident in private industry during the period indicated, there were approximately 500 lost workday cases and 1,000 recordable incidents, as defined by OSHA (Figure 1). Where Heinrich’s original work and this author’s recent work analyze past incident records, this article uses these past trends and generally accepted statistical methods [3] in an attempt to predict potential future pat- terns. The purpose of this article is to present these analyses so that conclusions seful to safety profession- u 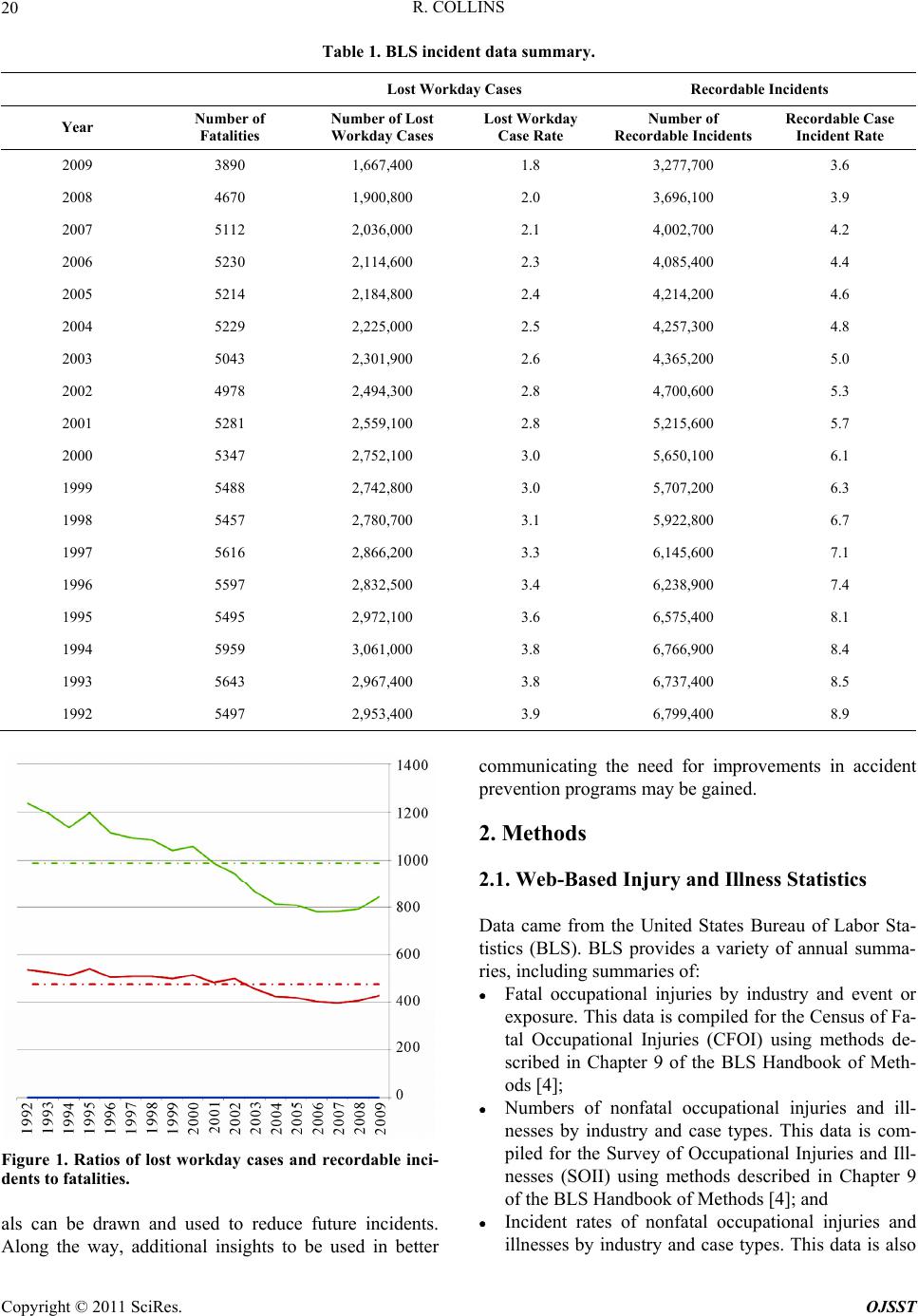 R. COLLINS 20 Table 1. BLS incident data summary. Lost Workday Cases Recordable Incidents Year Number of Fatalities Number of Lost Workday Cases Lost Workday Case Rate Number of Recordable Incidents Recordable Case Incident Rate 2009 3890 1,667,400 1.8 3,277,700 3.6 2008 4670 1,900,800 2.0 3,696,100 3.9 2007 5112 2,036,000 2.1 4,002,700 4.2 2006 5230 2,114,600 2.3 4,085,400 4.4 2005 5214 2,184,800 2.4 4,214,200 4.6 2004 5229 2,225,000 2.5 4,257,300 4.8 2003 5043 2,301,900 2.6 4,365,200 5.0 2002 4978 2,494,300 2.8 4,700,600 5.3 2001 5281 2,559,100 2.8 5,215,600 5.7 2000 5347 2,752,100 3.0 5,650,100 6.1 1999 5488 2,742,800 3.0 5,707,200 6.3 1998 5457 2,780,700 3.1 5,922,800 6.7 1997 5616 2,866,200 3.3 6,145,600 7.1 1996 5597 2,832,500 3.4 6,238,900 7.4 1995 5495 2,972,100 3.6 6,575,400 8.1 1994 5959 3,061,000 3.8 6,766,900 8.4 1993 5643 2,967,400 3.8 6,737,400 8.5 1992 5497 2,953,400 3.9 6,799,400 8.9 Figure 1. Ratios of lost workday cases and recordable inci- dents to fatalities. als can be drawn and used to reduce future incidents. Along the way, additional insights to be used in better communicating the need for improvements in accident prevention programs may be gained. 2. Methods 2.1. Web-Based Injury and Illness Statistics Data came from the United States Bureau of Labor Sta- tistics (BLS). BLS provides a variety of annual summa- ries, including summaries of: Fatal occupational injuries by industry and event or exposure. This data is compiled for the Census of Fa- tal Occupational Injuries (CFOI) using methods de- scribed in Chapter 9 of the BLS Handbook of Meth- ods [4]; Numbers of nonfatal occupational injuries and ill- nesses by industry and case types. This data is com- piled for the Survey of Occupational Injuries and Ill- nesses (SOII) using methods described in Chapter 9 of the BLS Handbook of Methods [4]; and Incident rates of nonfatal occupational injuries and illnesses by industry and case types. This data is also Copyright © 2011 SciRes. OJSST  R. COLLINS21 compiled for the Survey of Occupational Injuries and Illnesses (SOII) using methods described in Chapter 9 of the BLS Handbook of Methods [4]. It should be noted that these annual summaries are the result of statistical analyses of raw data collected by BLS from representative businesses within the industries mentioned. Access to the underlying raw data is severely restricted. Moreover, the raw data collected by BLS is only a sample collected to represent all businesses/estab- lishments in the United States. Therefore, the data sum- maries provided by BLS are statistical summaries of samples collected in a manner so as to be representative of all businesses/establishments in the United States. Without access to the underlying raw data, we cannot know the shape of the data’s distribution or the distribu- tion of data for all businesses/establishments in the United States. Without knowledge of the shape of the underlying data, we cannot know whether to use para- metric or nonparametric statistical methods to analyze the data in these summaries. Fortunately, the Central Limit Theorem allows to assume that the sample means and confidence limits obtained from summaries of the underlying raw data are normally distributed because the sample size is so very large. Had the underlying raw data been available for analyses, the work presented in this article would have benefited greatly. However, the amount and variety of summary data available from the underlying raw data is sufficient to allow us to perform useful statistical analyses. 2.2. Data Management Trends during 1992-2009 were analyzed to determine the annualized and overall ratios of recordable incidents and lost workday cases to fatal occupational injuries. This data was used to determine the probability of experienc- ing a fatal occupational injury per incident resulting in an OSHA recordable incident for the time interval analyzed. If we assume that accident prevention programs do not change substantially over the next few years, these probabilities derived from past incidents can be used to predict future trends. With this assumption, probabili- ties derived from these past incidents are used with gene- rally accepted statistical methods to estimate the future likelihood of fatal accident occurrence. 2.3. Data Analysis The statistical methods chosen for this analysis are those derived from Binomial distributions and Poisson distri- butions. Binomial distribution methods are used because they represent 1) a series of n independent events or tri- als, 2) each of which can have only two possible out- comes. In this case, a chronological series of OSHA re- cordable incidents is the series of n independent events or trials used. “Two events are statistically independent if the probability of their occurring jointly equals the pro- duct of their respective probabilities (i.e., Pr(A∩B) = Pr(A) X Pr(B)).” [5] Each independent event is an inci- dent resulting in an OSHA recordable incident that can either result in a fatal or non-fatal injury. As can be seen, a Binomial distribution is suitable for this analysis. For recordable incidents alone, there are only two pos- sibilities going forward. These are: 1) The recordable incident will result in a fatality; or 2) The recordable incident will not result in a fatality. These are mutually exclusive and independent events, otherwise known as a Bernoulli Variable. A toss of a coin is a simpler example of a Bernoulli Variable. In each case, the event can take on only 1 of 2 possible values. Each toss of the coin or, in this case, recordable incident represents a single Bernoulli Trial producing a single result. When looking at a string of successive Bernoulli Trials, the appropriate statistical method to use in predicting potential future events of this type is a Bi- nomial distribution. If we wanted to calculate the pro- bability of having n successive trials before encountering z specified outcomes, we would use the following gene- ralized formula: ! Probability 1 !! nz z npp zn z where: n = Total number of consecutive trials or, in this case, recordable incidents without a single fatality; z = Total number of successes (or failures) or, in this case, one or more fatalities; p = Probability of a single success or failure (i.e., the probability of one or more fatalities given n consecutive recordable incidents). Unfortunately, analysis using a Binomial distribution alone gets us only part of the distance to a true temporal probability relationship. In order to establish a temporal probability relationship, a Poisson distribution must be used. Poisson distributions are usually associated with rare events. In this case, the rare event is a fatal occupa- tional incident. Fortunately, Poisson distributions can be used to approximate a Binomial distribution, under cer- tain conditions. Generally accepted statistics theory al- lows the use of a Poisson distribution to approximate a Binomial distribution when the value of n (i.e., total number of consecutive trials) is large and the value of p (i.e., the probability of a single success or failure) is small. In this case, the value of p is certainly small (i.e., p = 1/987 = 1.01 × 10−3 ± 8.14%) and the value of n in- creases with time. This means that the approximation of a Binomial distribution using a Poisson distribution im- Copyright © 2011 SciRes. OJSST  R. COLLINS Copyright © 2011 SciRes. OJSST 22 calculate. proves with time. In this case, we will use the Binomial distribution formula presented above to determine the probability of having n successive OSHA recordable incidents without a single fatality. In order to determine this probability, we must first determine the probability of having n suc- cessive OSHA recordable incidents without a single success or failure (i.e., zero fatalities) using the single event probability provided above (i.e., p = 1/987 = 1.01 × 10−3 ± 8.14%). This simplifies the formula as follows: Probability using a Poisson distribution can be calcu- lated using the following formula: e Probability ! k k where: µ = Mean of the Poisson distribution = λt; Λ = Number of events per unit time or number of fa- talities per unit time; t = Selected time interval; k = Total number of successes (or failures) or, in this case, one or more fatalities. 00 3 zero fatalities Probability1.01100.999 n Microsoft Excel and Stata/IC software (version 11, StataCorp LP, College Station, Texas, USA) were used for all of the statistical data analyses presented in this paper. An alpha of p < 0.05 was selected as the level of significance. As this is the probability of having zero fatalities in n successive OSHA recordable incidents, the probability of having one (1) or more fatalities in n successive OSHA recordable incidents can be determined using the fol- lowing formula: one (1) or more fatalities 00 3 zero fatalities Probability 1Probability11.01100.999 n 3. Results BLS data for all private industry has been extracted and summarized in Table 1 from on-line summary tables. When this data is normalized to the number of fatalities, Figure 1 was created to show the ratio of recordable incidents and lost workday cases to fatalities along with the average values over the 18-year period shown. The means and 95% confidence intervals for these ratios are shown in Table 2. Over the 18-year interval studied, there were an average of 987 recordable incidents and 476 lost workday cases for each fatality. If we assume these ratios to be predictive as well as historical, we can use them to determine the probability of future private industry fatalities. The 95% confidence intervals (as percents of the mean, shown in Table 2) can be consi- dered to be error associated with the probabilities we Collectively, these formulas produce the graph shown in Figure 2. The x axis in Figure 2 represents the num- ber of successive OSHA recordable incidents. In this graph, the solid line represents the probability of having n successive OSHA recordable incidents without having a single fatality (i.e., zero fatalities). The dashed line is the statistical complement to this (i.e., 1 – Probabilityzero fatalities) showing the probability of having 1 or more fa- talities in n successive OSHA recordable incidents. The lighter lines above and below both of these lines repre- sent the upper and lower bounds, given the error pro- duced at the 95% confidence level (i.e., = 0.05). As can be seen, the probability of having n successive OSHA recordable incidents without a single fatality Table 2. Ratios for all private industry and select industry groups. 95% Confidence Limits Mean Lower Limit Upper Limit % Error All Private Industry: Ratio of OSHA Recordable Inc i dents to Fatalities 987 906 1,067 ± 8.14 Ratio of OSHA Lost Workday Cases to Fatalities 476 451 502 ± 5.27 NAICS Code 238 (Specialty Trade Contractors Industry Group): Ratio of OSHA Recordable Incidents to Fatalities 442 407 477 ± 7.83 Ratio of OSHA Lost Workday Cases to Fatalities 221 209 232 ± 5.11 NAICS Code 211 (Oil and Gas Extraction Industry Group): Ratio of OSHA Recordable Incidents to Fatalities 167 142 191 ± 14.4 Ratio of OSHA Lost Workday Cases to Fatalities 93 76 109 ± 17.4 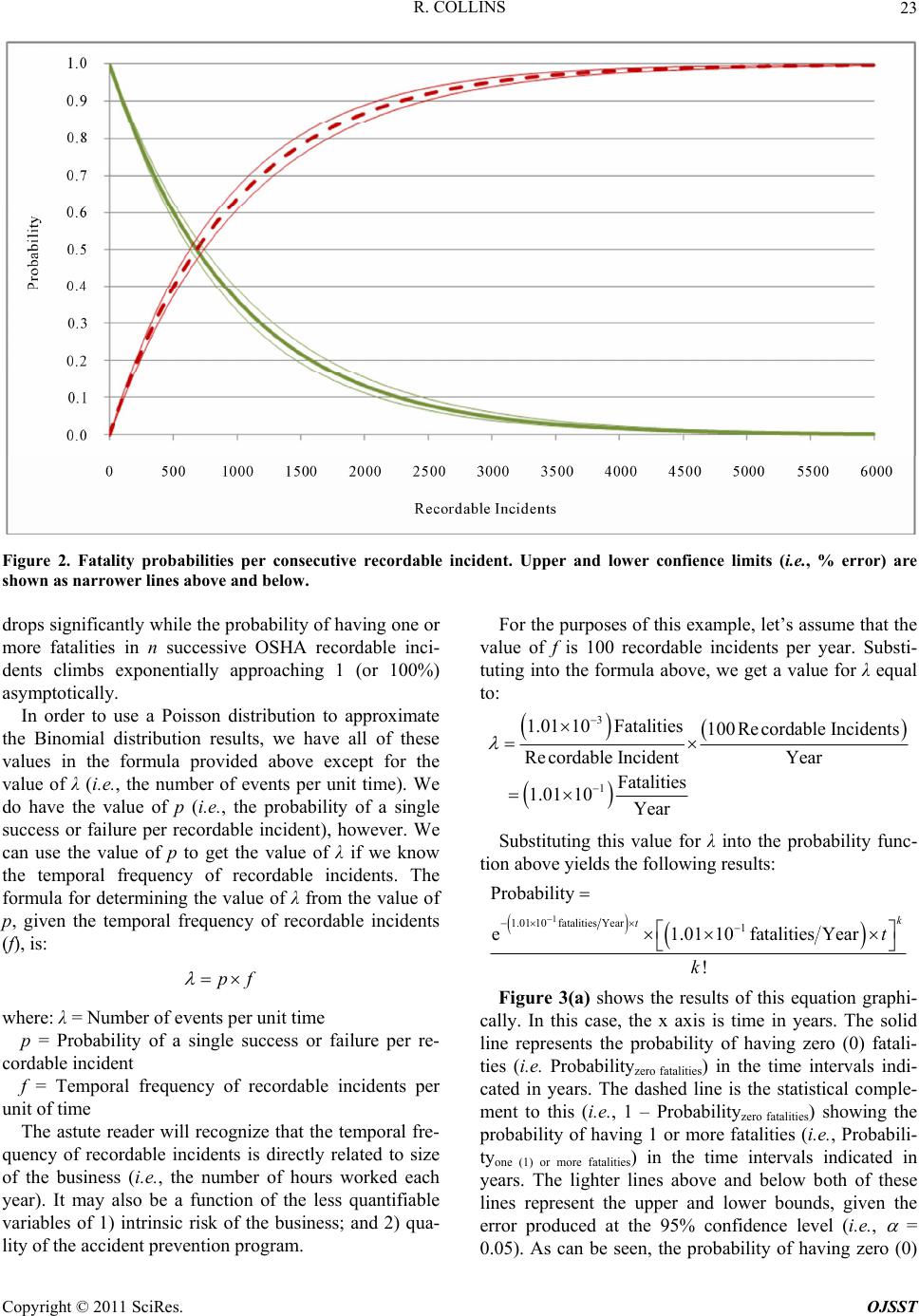 R. COLLINS23 Figure 2. Fatality probabilities per consecutive recordable incident. Upper and lower confience limits (i.e., % error) are shown as narrower lines above and below. drops significantly while the probability of having one or more fatalities in n successive OSHA recordable inci- dents climbs exponentially approaching 1 (or 100%) asymptotically. In order to use a Poisson distribution to approximate the Binomial distribution results, we have all of these values in the formula provided above except for the value of λ (i.e., the number of events per unit time). We do have the value of p (i.e., the probability of a single success or failure per recordable incident), however. We can use the value of p to get the value of λ if we know the temporal frequency of recordable incidents. The formula for determining the value of λ from the value of p, given the temporal frequency of recordable incidents (f), is: pf where: λ = Number of events per unit time p = Probability of a single success or failure per re- cordable incident f = Temporal frequency of recordable incidents per unit of time The astute reader will recognize that the temporal fre- quency of recordable incidents is directly related to size of the business (i.e., the number of hours worked each year). It may also be a function of the less quantifiable variables of 1) intrinsic risk of the business; and 2) qua- lity of the accident prevention program. For the purposes of this example, let’s assume that the value of f is 100 recordable incidents per year. Substi- tuting into the formula above, we get a value for λ equal to: 3 1 1.01 10Fatalities100Recordable Incidents Recordable IncidentYear Fatalities 1.0110Year Substituting this value for λ into the probability func- tion above yields the following results: 1 1.01 10fatalitiesYear1 Probability e1.0110fatalities Year ! k tt k Figure 3(a) shows the results of this equation graphi- cally. In this case, the x axis is time in years. The solid line represents the probability of having zero (0) fatali- ties (i.e. Probabilityzero fatalities) in the time intervals indi- cated in years. The dashed line is the statistical comple- ment to this (i.e., 1 – Probabilityzero fatalities) showing the probability of having 1 or more fatalities (i.e., Probabili- tyone (1) or more fatalities) in the time intervals indicated in years. The lighter lines above and below both of these lines represent the upper and lower bounds, given the error produced at the 95% confidence level (i.e., = 0.05). As can be seen, the probability of having zero (0) Copyright © 2011 SciRes. OJSST  R. COLLINS 24 fatalities drops significantly while the probability of having one or more fatalities in the time intervals indi- cated in years climbs exponentially approaching 1 (or 100%) asymptotically. For this example of 100 record- able incidents per year, the probability of having one or more fatalities exceeds 50% after only 7 years. If we were to use a different example, say 10 record- able incidents per year, the graph (Figure 3(b)) would appear the same but the x axis would reach further into the future. In this example, when the x axis is expanded to 500 years the graph is very similar in appearance. For 10 recordable incidents per year, the probability of hav- ing one or more fatalities exceeds 50% after only 69 years. 4. Discussion It should be noted that the ratios of 477 lost workday cases per fatality and 987 recordable incidents per fatal- ity (i.e., 1:477:987) were derived for all private industry. In reality, private industry within the United States is made up of dozens of business types and thousands of (a) (b) Figure 3. Fatal probability per year for all Private Industry. Solid line indicates the probability of zero (0) fatalities per year while the dashed line indicates the probability of one (1) or more fatalities per year. Lighter shaded lines above and below represent the upper and lower confidence limits (i.e., % error). Figure 3(a) assumes a rate of 100 recordable incidents per ear. Figure 3(b) assumes a rate of 10 recordable incidents per year. y Copyright © 2011 SciRes. OJSST  R. COLLINS Copyright © 2011 SciRes. OJSST 25 individual businesses. It is unlikely that all business types and individual businesses would have the same risk profile. We can see this by looking at two specific exam- ples. In the most recent year for which records are avail- able (i.e., 2009), Specialty Trade Contractors (North American Industrial Classification System or NAICS Code 238) had the highest total number of fatalities (i.e., 477) while Oil and Gas Exploration firms (NAICS Code 211) had among the lowest total number of fatalities (i.e., 17). When we apply the same methodology used above to characterize risk within private industry, we get the risk profiles shown in Table 2. From these results, it can be seen that the risk profile for private industry (i.e., 1:476:987) is significantly different from the risk profiles for Specialty Trade Contractors (i.e., 1:221:442) and Oil and Gas Exploration (i.e., 1:93:167). These risk profiles have nothing to do with the size of the business (i.e., the number of hours worked each year) and everything to do with those less quantifiable variables of 1) the intrinsic risk of their businesses; and/or 2) the quality of their ac- cident prevention programs. In any event, different risk profiles mean different probabilities for a single success or failure (i.e., p) that can be applied as above. The resulting probability graphs (Figure 4(b) for Specialty Trade Contractors and Figure 4(c) for Oil and Gas Exploration), assuming 100 record- able incidents per year, appear very similar to that for all private industry (i.e., Figure 4(a)) with only a shift to the right or left on the x axis. However, as can be seen, the probability of having one or more fatalities exceeds 50% after 3 years for Specialty Trade Contractors (NAICS Code 238) and 1 year for Oil and Gas Extraction (NAICS Code 211), assuming an annual rate of 100 re- cordable incidents per year. This would seem to indicate that working in the Oil and Gas Extraction industry group (NAICS Code 211) is more dangerous (at least from the likelihood of death following an incident) than it is in the Specialty Trade Contractors industry group (NAICS Code 238) and working in either industry group appears to be more dangerous than working in private industry as a whole. This is an especially interesting re- sult, given that two industry groups with diametrically opposite fatality totals during 2009 (i.e., 17 and 477) were chosen. This may be explained by the fact that, based upon hours worked, the Oil and Gas Extraction industry group (NAICS Code 211) is 1/10th of the size of the Specialty Trade Contractors industry group (NAICS Code 238) and this group is 1/100th of the size of all pri- vate industry. This same type of refined analysis can be applied to an individual business/establishment if there is sufficient historical data on which to base a potential future prob- ability. Figure 5 shows how this might be applied to a single business/establishment. The x axis in this figure represents years while the y axis represents probability. The solid line descending from left to right represents the probability of experiencing zero (0) fatal incidents for the general industry type corresponding to a specific business/establishment while the dashed line descending from left to right represents the same probability for a specific business/establishment. The solid line ascending from left to right represents the probability of one (1) or more fatal incidents for the general industry type corre- sponding to a specific business/establishment while the dashed line descending from left to right represents the same probability for a specific business/establishment. The vertical dashed line represents the current position in time on the graph for this specific business/establishment. Two (2) potentially valuable lessons that can be learned from this figure are: 1) The dashed lines representing a specific business/ establishment are to the left of the solid lines represent- ing the general industry type to which the specific busi- ness/establishment belongs. This can be interpreted as meaning that it is more dangerous to work in this specific business/establishment than it is for the group to which this business/establishment belongs. 2) At the specific point in time indicated by the verti- cal dashed line, the probability that the next OSHA re- cordable incident will result in a fatal accident is 35.6% for the specific business/establishment while it would only be 19.9% for the group to which this business/es- tablishment belongs. It should be noted, however, that an individual busi- ness/establishment will be a subset of the industry group to which it belongs. Moreover, both the Oil and Gas Ex- traction industry group (NAICS Code 211) and the Spe- cialty Trade Contractors industry group (NAICS Code 238) are subsets of the larger private industry group. While restricting this analysis to a specific industry group or business/establishment might produce more useful results, the confidence interval size (i.e., error) must of necessity increase as well making the results potentially less reliable. Statistically speaking, confi- dence intervals tend to increase as the sample size de- creases. In practice, however, two (2) different busi- nesses within the same industry group may have widely different approaches to accident prevention. A business with limited efforts to prevent accidents, sometimes known as a poor safety culture, may find their accident prediction curve (i.e., the Poisson distribution demon- strated above) shifted to the left compared to the industry group. Whereas, a business with strong efforts to prevent accidents, sometimes known as an excellent safety cul- ture, may find their accident prediction curve shifted to the right. In this example, smller sample sizes are more a 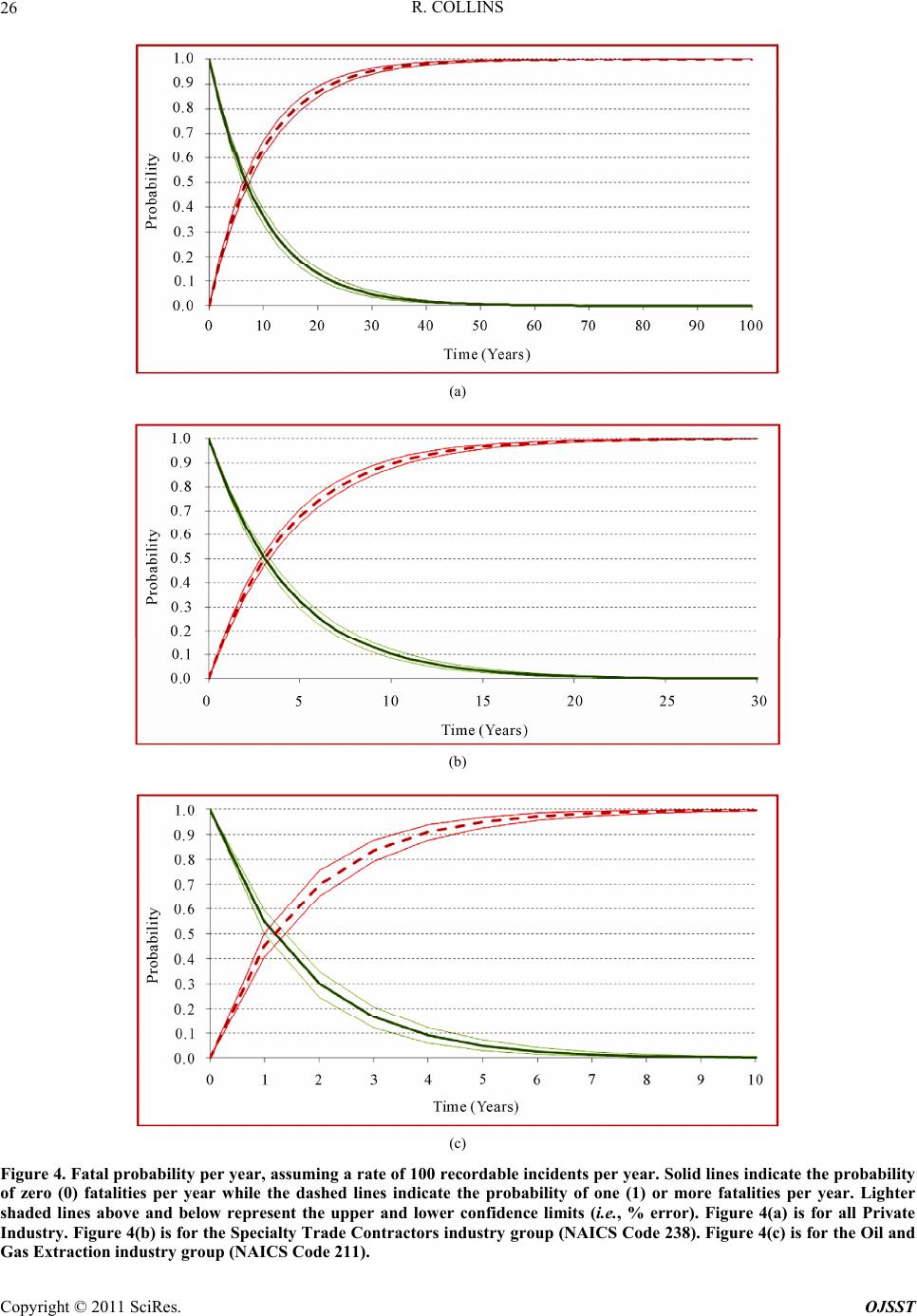 R. COLLINS 26 (a) (b) (c) Figure 4. Fatal probability per year, assuming a rate of 100 recordable incidents per year. Solid lines indicate the probability of zero (0) fatalities per year while the dashed lines indicate the probability of one (1) or more fatalities per year. Lighter shaded lines above and below represent the upper and lower confidence limits (i.e., % error). Figure 4(a) is for all Private Industry. Figure 4(b) is for the Specialty Trade Contractors industry group (NAICS Code 238). Figure 4(c) is for the Oil and Gas Extraction industry group (NAICS Code 211). Copyright © 2011 SciRes. OJSST 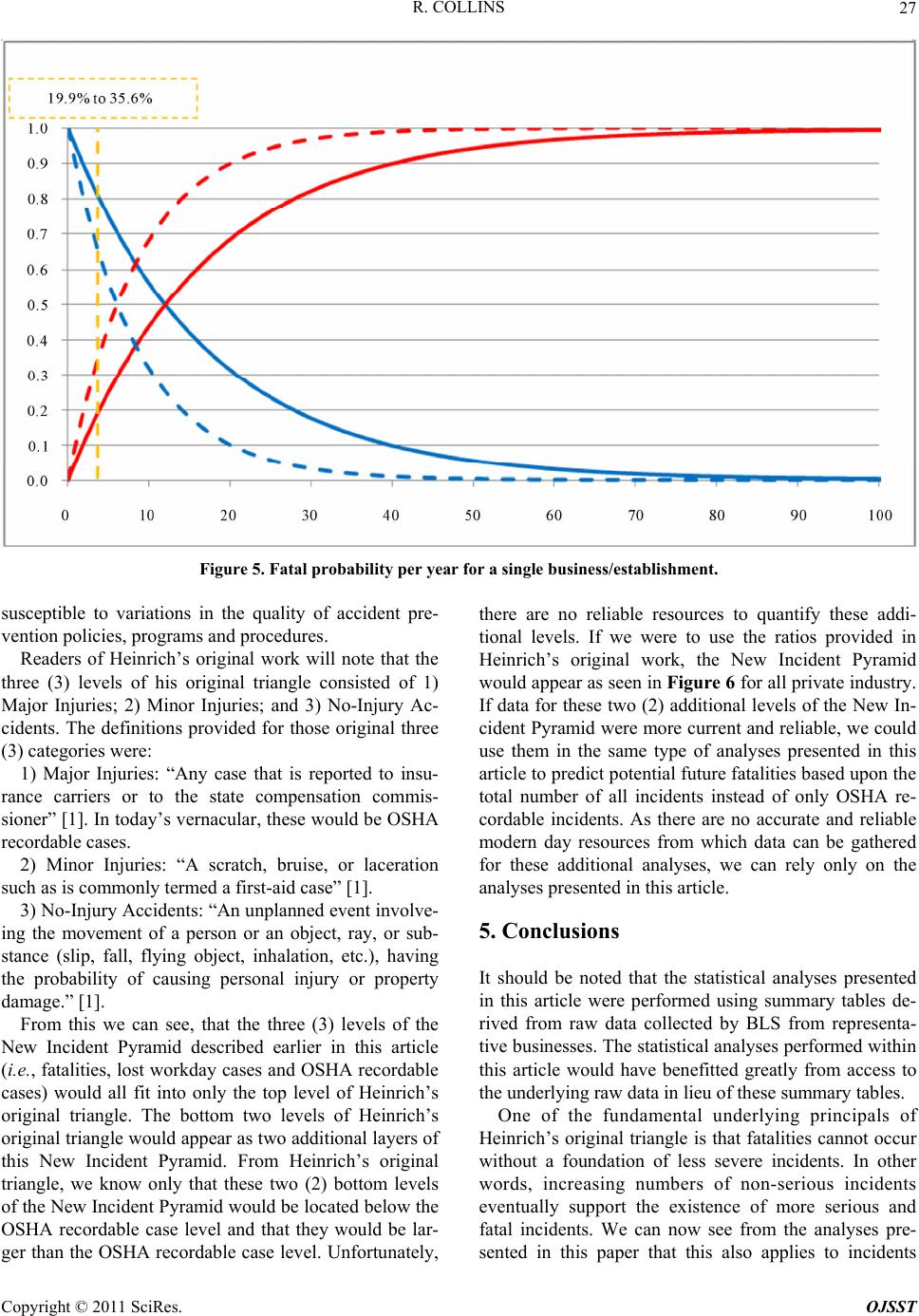 R. COLLINS27 Figure 5. Fatal probability per year for a single business/establishment. susceptible to variations in the quality of accident pre- vention policies, programs and procedures. Readers of Heinrich’s original work will note that the three (3) levels of his original triangle consisted of 1) Major Injuries; 2) Minor Injuries; and 3) No-Injury Ac- cidents. The definitions provided for those original three (3) categories were: 1) Major Injuries: “Any case that is reported to insu- rance carriers or to the state compensation commis- sioner” [1]. In today’s vernacular, these would be OSHA recordable cases. 2) Minor Injuries: “A scratch, bruise, or laceration such as is commonly termed a first-aid case” [1]. 3) No-Injury Accidents: “An unplanned event involve- ing the movement of a person or an object, ray, or sub- stance (slip, fall, flying object, inhalation, etc.), having the probability of causing personal injury or property damage.” [1]. From this we can see, that the three (3) levels of the New Incident Pyramid described earlier in this article (i.e., fatalities, lost workday cases and OSHA recordable cases) would all fit into only the top level of Heinrich’s original triangle. The bottom two levels of Heinrich’s original triangle would appear as two additional layers of this New Incident Pyramid. From Heinrich’s original triangle, we know only that these two (2) bottom levels of the New Incident Pyramid would be located below the OSHA recordable case level and that they would be lar- ger than the OSHA recordable case level. Unfortunately, there are no reliable resources to quantify these addi- tional levels. If we were to use the ratios provided in Heinrich’s original work, the New Incident Pyramid would appear as seen in Figure 6 for all private industry. If data for these two (2) additional levels of the New In- cident Pyramid were more current and reliable, we could use them in the same type of analyses presented in this article to predict potential future fatalities based upon the total number of all incidents instead of only OSHA re- cordable incidents. As there are no accurate and reliable modern day resources from which data can be gathered for these additional analyses, we can rely only on the analyses presented in this article. 5. Conclusions It should be noted that the statistical analyses presented in this article were performed using summary tables de- rived from raw data collected by BLS from representa- tive businesses. The statistical analyses performed within this article would have benefitted greatly from access to the underlying raw data in lieu of these summary tables. One of the fundamental underlying principals of Heinrich’s original triangle is that fatalities cannot occur without a foundation of less severe incidents. In other words, increasing numbers of non-serious incidents eventually support the existence of more serious and fatal incidents. We can now see from the analyses pre- sented in this paper that this also applies to incidents Copyright © 2011 SciRes. OJSST  R. COLLINS 28 Figure 6. New incide nt pyramid for all private industry. occurring over time. Valuable conclusions that can be drawn from this analysis include: 1) Fatal accidents are inevitable. Each day that passes without a fatal occupational accident only leads to an increased likelihood that a fatal occupational accident will occur during the next day as the probability ap- proaches 100% asymptotically. This conclusion may be dependent on the occurrence of less severe incidents as well as recordable incidents, as demonstrated by the adaption of Heinrich’s original triangle shown in Figure 6. 2) Factors potentially affecting when these fatalities will occur include: a) Size of the business (i.e., number of hours worked each year); b) Intrinsic risk of the business; and/or c) Quality of the accident prevention program. As only one (1) of these factors is within the direct control of business managers, the likelihood of a poten- tial future fatal accident can only be decreased by con- tinually improving the quality of their accident preven- tion programs. Perhaps the central lesson to be learned from these analyses is that we must always look on recordable inci- dents (and even accidents without injuries) as portents of fatal accidents to come. Doing little to prevent recordable or minor accidents today will only lead to fatal incidents sooner rather than later; if we do not respond appropri- ately when they occur. It is only by considering safety and accident prevention with our every thought and ac- tion that we can hope to push these fatal accidents further off into the future by shifting our own personal probabi- lity distribution to the right. 6. References [1] H. H. William, “Industrial Accident Prevention: A Scien- tific Approach,”4th Edition, McGraw-Hill Book Com- pany, Boston, 1959. [2] R. L. Collins, “Heinrich and Beyond,” Process Safety Progress, Vol. 30, No. 1, 2011, pp. 2-5. [3] B. Rosner, “Fundamentals of Biostatistics,” Brooks/Cole, Copyright © 2011 SciRes. OJSST  R. COLLINS29 Pacific Grove, 2010. [4] United States, “BLS Handbook of Methods,” The Bureau, Washington, 1982. [5] “McGraw-Hill Dictionary of Scientific and Technical Terms,” McGraw-Hill, New York, 2003. Copyright © 2011 SciRes. OJSST |

