Journal of Biosciences and Medicines
Vol.03 No.03(2015), Article ID:54782,5 pages
10.4236/jbm.2015.33007
3D Numerical Simulation of Epidermal Skin Turnover Process Using a Particle Model
Katsuya Nagayama1, Takahiro Uehara1, Yasuko Amano2, Masanori Tanahashi2
1Kyushu Institute of Technology, Fukuoka, Japan
2Kao Corporation, Tokyo, Japan
Email: nagayama@mse.kyutech.ac.jp


Received January 2015

ABSTRACT
Skin is the largest organ of the human body. In recent years, concern regarding the cosmetics area has increased, and research studies on anti-aging therapy or cosmetics have been rapidly conducted. Skin cells are not only changing its shape but also its physical properties during the epidermal skin turnover process. Computational simulation can be useful in further understanding the mechanisms of skin formation. We propose a particle model that can handle complex biological phenomena, including cell interactions and is a suitable method for simulating skin formation. The particle model was applied to simulate three-dimensional skin formation accompanied by proliferation and cornification of skin cells. The simulation results represented and reproduced the epidermal skin turnover phenomenon.
Keywords:
Numerical Simulation, Skin Formation, Particle Model

1. Introduction
Skin is the largest organ of the human body. We can check for an epidermal condition and provide appropriate care, particularly because the epidermis is the most external part of the skin [1]. In recent years, concern regarding the cosmetics area has increased in both men and women; thus, prompting research studies on anti-aging therapy or cosmetics. Skin cells change not only its shape but also its physical properties during the turnover process. Computational simulation can be useful in further understanding the mechanisms of skin development, and several models have been proposed [2]-[5]. We propose a particle model that can handle complex biological phenomena, including cell interactions such as cell division, motion, deformation, and transition [6] [7]. Furthermore, it is a suitable method for simulating skin formation [7]-[9].
This study developed an analytical method for the formation and turnover process in skin using a particle model. Numerical simulations of the epidermal skin formation process that includes cell division and cell transformation were conducted based on a three-dimensional (3D) non-spherical model. The objectives of this study were to clarify the mechanism of skin formation and to contribute additional information to the area of skin beauty. We used numerical simulations to understand and clarify these phenomena. The model could be applied to the diagnostic system of skin beauty.
2. Analysis Object and Model Description
2.1. Analysis Object
Figure 1 presents a cross-section of the skin [1], and the roles of each cell layer are described. The epidermis is the outermost layer of the skin and is primarily composed of cells called keratinocytes. The epidermis consists of four layers. A basal layer, which is the lowermost layer of the epidermis, provides new cells by dividing each day. The dividing cells are called the prickle layer, which are pushed and moved upward to the skin surface, transforming into the granular layer and stratum corneum and finally detach from the skin surface. Skin cells change not only their shape but also their physical properties during this process. This process is referred to as turnover and occurs at approximately 4-week intervals.
2.2. Model Description
A particle model [6] [7] is introduced to simulate the skin formation process [8] [9]. The model considers the interaction between the particles and pursues motions of the particles in a Lagrangian way. This method is suitable for analysis with large deformations or when the number of calculation point is changing. The cellular particles move in response to inter-particle forces, such as volume conservation force and spring force. The volume conservation force F in Equation (1) works to keep the distance between the particles. Because of the repulsive force, particles eventually move to a stable distance. Here, k is a coefficient, ddr is the distance between two particles, dr0 is the standard distance, which is 12.4 µm in this case, a and r are conversion factors for the movement of the non-spherical particles, where a is the particle size of the target and r is the reference particle diameter. The spring force f in Equation (2) works to make the continuum of the cellular particles structural. Here, k' is the coefficient of elastic spring. As the skin is formed, the particles are increasingly connected with the surrounding particles, the spring force between the particles become strong, and finally, the particles form an elastic solid. In Equation (3), by summing up these forces from the surrounding particles, the particles gradually move to the position of the force balance. x and x' are the positions before and after movement by these forces. α and β are coefficients, and its values are 1 and 1/300, respectively.
 (1)
(1)
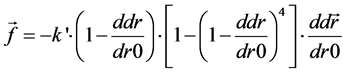 (2)
(2)
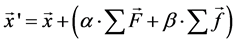 (3)
(3)
Figure 2 shows a flow chart of the steps of the analysis in the present study. Initially, the basal layer cells are placed and fixed. The new cells are divided from the basal cell layer and split from them. Inter-particle force in Equation (1) and the spring force in Equation (2) are calculated. Next, the cells are moved toward the surface using Equation (3), simultaneous with changes in its shape and physical properties. The calculations are again conducted and finally, the results of the calculations are generated.
3. Calculation Conditions
Two-dimensional (2D) and 3D models are analyzed. The initial placement of both the models shown in Figure 3 can be configured only at the dermis and basal layer. The basic model of initial cell particles presents a
Figure 1. Cross-section of the skin [1].
Figure 2. Analysis flowchart.

Figure 3. Initial shapes. (a) Two-dimensional model; (b) There- dimensional model.
spherical shape with a 10-μm diameter. The shape changes with time becoming thinner in the granular layer and adopts an elliptical shape that extends in the transverse direction of approximately 1-μm in thickness in the stratum corneum. In addition, it is assumed that cell division occurs at a rate of 0.2 times per day from the basal cell. The divided cells freely move under a force to keep the volume constant until it reaches the granular layer. Spring force begins to gradually occur from the granular layer to the corneum layer and connects to each particle; therefore, migrations reduce, and finally, the structure is fixed.
In both 2D and 3D analyses, a case involving a basal layer with a flat shape and a case with an irregular shape were conducted. In 2D analysis, the cells in the granular layer have an elliptical shape that extends in the transverse direction. By representing the shape supplemented by a plurality of particles, the laminated structure of the stratum corneum was confirmed. In 3D analysis, the stratum corneum cells were represented as described in the outline, and the stacked state was investigated.
4. Results and Discussion
Figure 4 presents the results of the 2D model analysis of the epidermal skin metabolism. Figure 4(a) and Figure 4(b) show the flat basal layer and Figure 4(c) presents the rete ridge case. From the basal layer (light blue), prickle cells (yellow green) split and move upward, which then develops into the granular layer (yellow). Finally, the corneum (red) peels off. The cells in the course of the spinous layer transform within the stratum corneum into elliptical-shaped cells that extend from the spherical shape in the horizontal direction to form the skin. Calculations were conducted using the non-spherical model; display (a) uses sphere particles, and corneum particles (red) appear to overlap. However, the complement display of (b) matches the shape change of the cells in the calculation, which varies in an elliptical shape and extends from the spherical shape in the lateral direction to form the skin. Therefore, this model can represent the metabolic processes occurring in the skin.
Figure 4(c) shows a case where there is unevenness in the basal layer of the initial arrangement. The surface of the skin, including the basal layer irregularities is flat. Because cell particles move to a stable distance by volume conservation forces, the particles of the protrusion enter the gaps between the moving particles into the recess and adopt a flat shape. Even if irregularities in the basal layer of the stratum corneum of the actual skin become flat, calculation can reproduce the actual phenomena.
Figure 5 shows the results of 3D analysis of a case with and without the irregularities in the basal layer. In the case of a flat basal layer, Figure 5(a) is the cross-sectional view of the metabolism, and the top of the corneum layer is flat, which is similar to the 2D model. Figure 5(c) is the top view; the corneum is expressed as a circular outline, and it forms a layer covering the entire surface.
In case of an uneven basal layer, Figure 5(b) is the cross-sectional view of the metabolism, and the top of corneum layer is flat despite the uneven basal layer, which is similar to the 2D model. Figure 5(d) is the top view, and the corneum is expressed as circular outline. It forms a layer covering the entire surface.
A reversal of vertical positional relationship of the cell is observed at the boundary of each layer in both 2D and 3D models. This has occurred because it is controlled by a change from the basal layer cells into corneocytes as well as a change on its position and the surrounding space.
Figure 6 shows the relationship between the cell division frequency and epidermal skin thickness. In both 2D and 3D models, there is a tendency to frequently divide, resulting in greater skin thickness. This occurs at a

Figure 4. Results of two-dimensional epidermis simulation. (a) Flat model without cell shape complement; (b) Flat model with cell shape complement; (c) Rete ridge model.


Figure 5. Results of three-dimensional epidermis simulation using a different basal layer shape. (a) Flat model; (b) Rete ridge model; (c) Flat model; (d) Rete ridge model.
Figure 6. Cell division frequency and epidermal skin thickness.
certain time during peeling and after division. Skin aging is characterized by a decrease in cell division frequency resulting in thinner skin; the simulation effectively represents this phenomenon.
5. Conclusion
In this study, the formation and metabolism of skin was modeled using a particle model, and 2D and 3D numerical simulations were conducted. The model considers the cell division that forms the basal layer, and the cell shape changes from spherical prickle layer to thin elliptical shape of the corneum layer. At the bottom of the skin, the volume conservation force is dominant as the cells move upward, spring force gradually emerges and becomes dominant at the corneum surface. Simulation results show the flat surface of the skin for both cases of flat and uneven basal layers. The present study also confirmed that skin thickness changes as the cell division frequency varies. These results have facilitated the simulation of skin formation metabolism. By comparing these results to the actual phenomena and by elucidating the mechanism of skin epidermal skin turnover, this system can be potentially applied to beauty diagnostic systems.
Cite this paper
Katsuya Nagayama,Takahiro Uehara,Yasuko Amano,Masanori Tanahashi, (2015) 3D Numerical Simulation of Epidermal Skin Turnover Process Using a Particle Model. Journal of Biosciences and Medicines,03,45-49. doi: 10.4236/jbm.2015.33007
References
- 1. Saita, T. (2009) Introduction of Skin Histopathological Diagnostics. Nankodo Co., Japan, 2-13.
- 2. Querleux, B. (2014) Computational Biophysics of the Skin. Pan Stanford Publishing. http://dx.doi.org/10.1201/b17205
- 3. Sütterlin, T., Huber, S., Dickhaus, H. and Grabe, N. (2009) Modeling Multi-Cellular Behavior in Epidermal Tissue Homeostasis via Finite State Machines in Multi-Agent Systems. Bioinformatics, 25, 2057-2063. http://dx.doi.org/10.1093/bioinformatics/btp361
- 4. Hirashima, T., Hosokawa, Y., Iino, T. and Nagayama, M. (2013) On Fundamental Cellular Processes for Emergence of Collective Epithelial Movement. Biology Open, 2, 600-666. http://dx.doi.org/10.1242/bio.20134523
- 5. Adra, S., Sun, T., MacNeil, S., Holcombe, M. and Smallwood, R. (2010) Development of a Three Dimensional Multiscale Computational Model of the Human Epidermis. Open Journal PLoS ONE, 5, e8511. http://dx.doi.org/10.1371/journal.pone.0008511
- 6. Nagayama, K., Nitta, J. and Miura, I. (2009) Numerical Analysis on Angiogenesis in Cancer Using a Particle Model. Theoretical and Applied Mechanics Japan, 58, 321-324.
- 7. Hashiguchi, S. and Nagayama, K. (2011) Construction of a Hair Formation Analysis Method Using the Particle Model, 2011 Bioengineering Conference, 23th Japan Society of Mechanical Engineers, Japan, 9D-01, 355-356.
- 8. Uehara, T., Nagayama, K., Amano, Y. and Tanahashi, M. (2013) Numerical Simulation of Epidermal Skin Formation Using Particle Model. The 2nd BMIRC International Symposium on Frontiers in Computational Systems Biology and Bioengineering, Japan, 30 January 2013.
- 9. Amano, Y., Uehara, T., Tanahashi, M. and Nagayama, K. (2012) An Epidermal Turnover Model Predicts Uneven Skin Tone with Aging. SY01.01 ICBS (World Congress on the International Society for Biophysics and Imaging of the Skin), Copenhagen, 29 November 2012.





