Open Journal of Social Sciences
Vol.03 No.03(2015), Article ID:54748,7 pages
10.4236/jss.2015.33002
The Discriminate Analysis and Dimension Reduction Methods of High Dimension
Lan Fu1,2
1Statistics School, Jiangxi University of Finance of Economics, Nanchang, China
2Research Center of Applied Statistics, Jiangxi University of Finance of Economics, Nanchang, China
Email: fulan60010068@sina.com


Received September 2014

ABSTRACT
Statistical methods have been getting constant development since 1970s. However, the statistical methods of the big data are no longer restricted with these methods which are listed in the textbook. This paper mainly demonstrates the Discrimination Analysis of Multivariate Statistical Analysis, Linear Dimensionality Reduction and Nonlinear Dimensionality Reduction Method under the circumstances of the wide range of applications of high-dimensional data. This paper includes three parts. To begin with, the paper illustrates a developing trend from the data to the high-dimensional. Meanwhile, it analyzes the impacts of the high-dimensional data on discriminate analysis methods. The second part represents the necessity of the dimensionality reduction studies in the era of the high-dimensional data overflowing. Then, the paper focuses on introducing the main methods of the linear dimensionality reduction. In addition, this paper covers the basic idea of the nonlinear dimensionality reduction. Moreover, it systematically analyzes the breakthrough of the traditional methods. Furthermore, it chronologically demonstrates the developing trend of the dimensionality reduction method. The final part shows a comprehensive and systematic conclusion to the whole essay and describes a developing prospect of the dimension reduction methods in the future. The purpose of this essay is to design a framework of a performance system which is subject to the characteristics of China High-tech enterprises. It based on the analysing the principles and significance of the performance system of High-tech enterprises. The framework will promote the standardize management of High-tech enterprises of China.
Keywords:
High-Dimensional Data, Method of Dimensionality Reduction, Discriminant Analysis, Linear Dimensionality Reduction, Manifold Structure

1. Introduction
“The coming century is surely the century of data [1]”. People did have access to a large amount of financial data, image data and space data recently. These data have a common feature which is they are all high-dimen- sional data. Actually, most data people obtained are high-dimensional in the world. The increase of data dimension brings the Gospel of the dimension meanwhile leads to the data disaster. This information which is hidden by the high-dimensional data provides a possibility for solving the scientific problems. However, it is difficult to imagine the challenges of the data processing technology because of the increase of the data dimension.
The method of dimensionality reduction is defined as a low-dimensional expression way which can faithfully reflect the inherent feature of the raw data in high-dimensional data. It caused the widespread attention of people because the dimension reduction method is considered as an effective measure to prevent “the curses of dimensionality [2]” happening. So far people had found a lot of different dimension reduction methods which involve the Projection Pursuit Method, Principle Component Analysis (PCA) and Manifold Learning. However, the Isomer, Locally Linear Embedding (LLE) and Palladian Eigen map are all based on the Manifold Learning [3]. There are several different methods of division for the dimension reduction methods. According to the nature of data, the method of dimension reduction can be divided into Linear Dimensionality Reduction and Nonlinear Dimensionality Reduction. In terms of the geometrical structure of the preservation degree of the dimension reduction, it includes local approach and global approach. These dimension reduction methods obtain systematical analysis and contrast.
2. High-Dimensional Tendency of the Data and Its Impact
2.1. The Derivative of High-Dimensional Data
With the development of the science and technology, people can obtain a great deal of information to reveal the objective law which is covered by superficial phenomenon. This leads to a tendency which is the data is gradually development from the low-dimension to the high-dimension. In other words, the improvement of data dimension brings the Gospel of the dimension meanwhile result in the data disaster [4].
“The curses of dimensionality” was first put forward by Bellman in 1961. At that time, the curses of dimensionality refers to the incensement of the dimension would lead to an exponential growth of samples in certain statistical index model. Meanwhile, the indicating length and complexity of the processing information would have a exponential growth. Nowadays the curses of dimensionality mainly refer to the intrinsic sparsely in the high dimensional data space. In other words, it is the spatial representation in the high dimensional data space. “The curses of dimensionality” is caused by the intrinsic dimension rather than the representation dimension. It affects some fields which involve Statistical Estimation, Numerical Integration, Optimization Problems, and Probability Density Estimation so on. Thus, the dimension reduction method as a low-dimensional expression method of the high-dimensional data getting the essential characteristics of the original date can effectively avoid the curses of dimensionality. It causes the widespread attention of people.
2.2. Impact of High Dimensionality for Classification
There is a common problem in the process of classification. The size of the dimension p of feature vectors is much greater than the size of the training sample n. In addition, only a part of p feature vectors plays a important role in the classification. Although the traditional analysis method is extremely important, it is not suitable for high-dimensional case. The following statement illustrates the influences of the high-dimension for the Fisher discriminate analysis and independent classification criteria respectively. Besides, the statement assumes the discrimination occurs in the two high-dimensional populations. And the probability of the two populations is 50%. Meanwhile, there is comparability between Sample n1 and simple n2.
2.2.1. Fisher Discrimination Based on the High Dimensionality
The Fisher discriminate is . It can assure both
. It can assure both 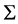 and
and  are non ill-conditioned matrix in the parameter space. It also can guarantee one of the Mahalanobis distances of two categories is positive C. Therefore, it can the utilizes
are non ill-conditioned matrix in the parameter space. It also can guarantee one of the Mahalanobis distances of two categories is positive C. Therefore, it can the utilizes  of the sample data estimation to obtain the asymptotic optimality in low-dimension situation. However, the situation is different from high-dimension. One reason is that the true covariance matrix is not ill-conditioned matrix. Another reason is that the abnormal value of the sample covariance is not suitable for the Fisher criterion because the situation of the size of dimensionality is greater than the size of the sample.
of the sample data estimation to obtain the asymptotic optimality in low-dimension situation. However, the situation is different from high-dimension. One reason is that the true covariance matrix is not ill-conditioned matrix. Another reason is that the abnormal value of the sample covariance is not suitable for the Fisher criterion because the situation of the size of dimensionality is greater than the size of the sample.
2.2.2. Impact of the Dimensionality for the Independent Criteria
The difficulties of the high-dimensional discriminated lie in a lot of noise characteristics. These noise characteristics have no any function for the reduction of the classification errors. There is another reason for the poor results of the Fisher discriminate under the high-dimensionality circumstances. That is people can individually estimates for each parameter. However, the error will be great as people estimate multiple feature estimation at the same time. Therefore, this will lead to the significant increase of the error probability [5].
3. The Main Method of the Dimension Reduction
3.1. The Classification of the Dimension Reduction Method
In the light of the nature of the data, the method of dimension reduction can be divided into Linear Dimensionality Reduction and Nonlinear Dimensionality Reduction. These two methods can be further divided into some mainstreaming classification methods and the details [6]. As shown Figure 1.
3.2. The Main Methods of the Linear Dimension Reduction
The linear dimension reduction method is most widely application in the dimensionality reduction. There are some excellent properties in the linear dimension reduction method. These properties involve easily explicable, an analytical solutions, simple calculation and the effectiveness of the linear structure of the data collection. As matter of fact, the linear dimensionality reduction method is based on the different optimization criterion. It seeks the best linear model. This is totally different with nonlinear dimensionality reduction method. However, it is the common property of all linear dimensionality reduction methods. The linear dimensionality reduction methods mainly include the Principal Component Analysis and the Linear Discriminate Analysis. The nonlinear dimensionality reduction methods [7]-[9] chiefly involve the Locally Linear Embedding, Palladian Eigen maps, Isomer, Multidimensional Scale Method and the Local Tangent Space Method so on.
3.2.1. Principal Component Analysis (PCA)
The Principal Component Analysis [10] was first put forward by Pearson (K.Pearson) in 1901. However, Hostelling (H. Hostelling) established a mathematical foundation for PCA in 1933. The theoretical basis of PCA is based on the karhunen-levy expansion. The basic idea of PCA is that the original variables can be transformed into several comprehensive variables which are able to reflect the main properties of the things. Meanwhile, the high-dimensional data can be shadowed on the low-dimensional space. This ensures a most effective low-di- mensional data in the least square sense and truly represents the original high-dimensional data. This method focuses on a fidelity optimization of the original high-dimensional data. It tries to solve a problem of the projection direction and obtain the representation of the original data in the least square sense.
From the mathematical point of view, the starting point of the principal component analysis is the sample covariance matrix S.
Figure 1. The classification of the dimension reduction method.

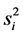 is the variance of the variable xi. Sij is the covariance between variable xi and variable xj.
is the variance of the variable xi. Sij is the covariance between variable xi and variable xj.
There is no linear correlation between the variables xi and the variables xj if the covariance is zero. The strength of the linear correlation between the variables xi and the variables xj can be expressed by the correlation coefficient Riy which is equal . The change of the main spindle would transform the number of p correlative variables
. The change of the main spindle would transform the number of p correlative variables 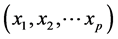 into the number of p uncreative variables
into the number of p uncreative variables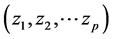 . The variable of the new axes described by an eigenvector
. The variable of the new axes described by an eigenvector .
.
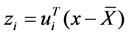
That is the ith principal components. (The mean of Zi is zero, the variance is li which is the ith eigenvalue.)
There are some main steps of the dimension reduction. The first step is to obtain the eigenvalues and the eigenvectors of the covariance matrix, then rank the size of the eigenvalues. The second step is to choose the eigenvector of the big eigenvalues corresponding and put this eigenvector as a projection vector. The final step is the high-dimensional data would be projected onto the subspace of the projection vector spanned.
Undoubtfully, there are some problems and limitations on the PCA. First of all, the PCA have to assume the approximate normality of the input space. Secondly, the PCA have to assume that the input data is real and continuous. Thirdly, the PCA will fail if the distribution of the data had the complex manifold structure.
3.2.2. Linear Discrimination Analysis (LDA)
The Linear Discrimination Analysis was first put forward by Fisher (R.Fisher) in 1936. The LDA is similar to the PCA. However, there are some differences between the LDA and the PCA.
There are some common points between LDA and LDA. Firstly, LDA and PCA both are obtained by a set of projection vectors, and utilize the high-dimension data to project the low-dimensional space. Therefore, LDA and PCA have the similar procedures. The second point is that the same purpose of LDA and PCA both are dimensionality reduction.
Obviously, there are some differences between LDA and PCA. First of all, the projection vectors of LDA and PCA are totally different. The reason is that the key point of LDA and PCA are different in the process of dimensionality reduction. PCA make the optimization of the original high-dimension data fidelity of the dimensionality reduction data as the key. It tries to get a direction of an optimal projection. Then the projection data can represent the original data as far as possible in the constraint conditions. However, LDA focus on the optimization of the different data discrimination of the dimensionality reduction data. The purpose of the LDA is Tyr as far as possible to separate the two types of data.
3.3 .The Major Methods of the Nonlinear Dimension Reduction
3.3.1. Local Linear Embedding (LLE)
The main steps of the Local Linear Embedding [11] [12] (LLE) include the following points.
The first step is to find a set of the K-nearest neighbors of each point. It means to compute a set of weights for each point that best describe the point as a linear combination of its neighbors. Then it uses an eigenvector-based optimization technique to find the low-dimensional embedding of points, such that each point is still described with the same linear combination of its neighbors. The Euclidean distance and Dijkstra distance of keeping the surface characteristics of sample points can be used in the distance computation.
The second step is to get a local reconstruction weight matrix of the sample through computing the neighbor point of each sample. Then it constructs a cost function to measure the reconstruction error. The cost function is expressed as

The W of the reconstruction weight is minimized under two constraints. One of the constraints is the W will be zero if point xi is not a neighbor of the point xj. Another constraint is . In other words, it is to get W. It means to solve the problem of the least square with constraint.
. In other words, it is to get W. It means to solve the problem of the least square with constraint.
The third step is to compute the output value of the sample by the local reconstruction weight matrix and the neighbor point of the sample. Each sample xi will be mapped onto the low-dimensional vector Y.
The main ideas of LLE include the following aspects. The first aspect is to assume each sample point and its neighbor point in a linear region of manifold. Another one is to transform the global nonlinear into the local linear and the local overlap fields of each sample and neighboring point can supply the global structure information.
3.3.2. Local Tangent Space Alignment (LTSA)
The emergence of the LTSA (2014) is later than other dimensionality reduction methods. The basis of the LTSA algorithm which is proposed by Zhang Zhenyue and other researchers include the following parts. One basis is that the LTSA can obtain a new global nonlinear structure by integrating the local linear information and local linear analysis. This structure has the properties of a nonlinear manifold. The LTSA includes two steps which are projection and integration.
The LTSA can properly show the good properties of the geometry feature of the manifold. But it also has limitations. These limitations indicate that the LTSA cannot do very well to the manifold learning for high curvature.
3.4. Dimensionality Reduction―From the Beginning to Nowadays
The study of the dimensionality reduction can be traced to 1901. The main methods of the dimensionality reduction include Linear Discriminate Analysis, Principal Component Analysis and Projection Pursuit so on. The developed dimensionality reduction methods in recent years mainly involve the Nonlinear Dimensionality reduction (It is based on kernel.), the dimensionality reduction of the two-dimensionality and tensor, the Manifold Learning and localized dimensionality reduction as well as Semi-supervised Dimensionality Reduction.
3.4.1. Nonlinear Dimensionality Reduction Based on the Kernel
Since Schölkopf (B. Schölkopf) and other researchers introduced the kernel methods to the field of the dimensionality reduction, they proposed the classic Kernel Principal Component Analysis. In addition, researchers combined with the kernel methods and other traditional dimensionality reduction methods. Then they proposed some discriminate analysis methods. These methods include Fisher Discriminate Analysis, Kernel Canonical Correlation Analysis and Kernel Independent Component Analysis.
So far, almost all of the linear dimensionality reduction methods have corresponding “kemelized version”. The kernel methods have become standard practice methods for a linear dimensionality reduction transforming into a no linearization dimensionality reduction. The key point is the selection of the kernel and the kernel parameter in the dimension reduction algorithm which is based on the kernel. Researchers also focus on improving the operational efficiency of the kernel dimensionality reduction algorithm in the big data.
3.4.2. Two-Dimensionalization and Tensor Dimensionality Reduction
The traditional model is defined as a sample point which is represented as a vector model of a point in n-dimen- sional space. It is obviously that the traditional model is more easily to be handled by various statistical methods. However, the traditional model is no longer suitable for application in practical under this situation. This situation is the sample is usually non-vector model and will transform two dimensional models into corresponding vector models. This situation would lead to the damage of the structure information of the original matrix and the adverse consequences of increased time cost and storage cost. Therefore, the concept of the tensor dimensionality reduction was proposed. The idea of two-dimensional matrix image feature extraction was first put forward by Liu (K. Liu). This idea avoids the above adverse consequences. That is people can directly withdraw the eigenvalues and not necessary to pull a image into a vector.
Since then, the method had access to the development and research from different angles. The Two-Dimen- sional Principal Component Analysis (2DPCA), Two-Dimensional Linear Discriminate Analysis (2DLDA) and Tow-dimensional Canonical Correlation Analysis (2DCCA) were proposed. The methods of two dimensionalization and tensor dimensionality reduction have the advantages of highly computing efficiency. Meanwhile, there are many experimental results which indicate the two-dimension method is obviously better than one-di- mensional method in some datasets.
Recently, the representation method of the two dimensionlization and tensor model has been widely applied in the fields of the machine learning, pattern recognition and computer recognition.
Tensor Linear Discriminate Analysis,The tensor linear discriminate algorithm tries to expand the distance between classes. Meanwhile, it tries to shrink the distance within a class. There are some similar between the thought of the tensor linear discriminate analysis and the traditional linear discriminate analysis. The differences is that the traditional linear discriminate analysis method is only to seek a projection vector xi as n-dimensional sample; N is the total sample; Xi belongs to the selection of classes ; NS is the sample of the sth categories; c is the number of categories for all samples. However, the tensor linear discriminate analysis method is to seek and obtain the process of a series of projection matrix. Then it transforms the tensor sample into the tensor data of the low dimension. Meanwhile it would maximize the class distance and minimize the within class distance.
; NS is the sample of the sth categories; c is the number of categories for all samples. However, the tensor linear discriminate analysis method is to seek and obtain the process of a series of projection matrix. Then it transforms the tensor sample into the tensor data of the low dimension. Meanwhile it would maximize the class distance and minimize the within class distance.
The tensor linear discriminate analysis method is to deal with samples and extract the features of samples in the tensor field. This can be considered as an extension of the traditional linear discriminate analysis method in the tensor subspace. Compared with vector, the tensor subspace effectively retained the sample information and made full use of the collecting information. At the same time, the tensor linear discriminate analysis method overcomes the issue of the small sample size in the traditional linear discriminate method and improves the learning performance.
3.4.3. Manifold Learning and Localized Dimensionality Reduction
The manifold learning has become a new hot research in machine learning field. This is happened in 2000 which is the year of the magazine “science” published two classic articles about the isometric mapping (ISOMAP) and locally linear embedding (LLE). The manifolding learning is another way to obtain nonlinear dimensionality reduction except for the kernel method. One of the basic assumptions of the manifold learning is to distribute samples on a potential manifold. Thus, the internal dimensionality of the manifold is generally not high even though the input space is the high-dimensional space.
After the emergence of Isomer and LLE method, there have been a number of other manifold learning algorithms. These algorithms involved maximum variance extension, Laplace feature mapping and local tangent space alignment so on. Compared with the traditional linear dimensionality reduction algorithm, the manifold learning can effectively solve the problem of the nonlinear. However, most manifold algorithms still have some issues about the low-efficiency of computing and difficult extending of the test samples.
The following algorithm has been improved for above problems respectively. The locally preserving projection is proposed by He (X. He) and other researchers is one of the most representatives. As a matter of fact, the locally preserving projection is the liberalized version of the Laplace feature mapping. There are many dimensionality reduction algorithms of the localization besides the locality preserving projections. These methods all utilized the thoughts of the local preservation. With the introduction of the class interval thoughts of the support vector machine, the dimensionality reduction algorithm of the nearest neighbor discriminate analysis was proposed. The comparison of the nearest neighbor discriminate analysis and locality preserving projection shows that the nearest neighbor discriminate analysis not only can integrate category information but also can obtain the dimensionality reduction of the optimal discriminate ability. Recently, a relevant typical example was proposed in the scientific field. Yan (S. Yan) and other researchers proposed a general framework of the map embedding. Most of the above dimensionality reduction methods was involved in this framework. The construction and the selection of parameters of a map is the key step in the dimension redaction methods of the map embedding.
4. The Summary and Prospect of the Dimension Reduction Methods
Undoubtfully, data dimensionality reduction is an effective tool for the work of the data digging. That information which is hidden by the high-dimensional data provides a possibility for solving the scientific problems. This possibility is depending on the improvement and development of the dimension reduction methods. The dimension reduction method can obtain an effectively low-dimensional representation and a way of the essential characteristics of reflecting the original data. Then the method of processing low-dimensional data can be used. This can avoid “data disaster”. In terms with the nature of the data, the method of dimension reduction can be divided into two categories. One category is Linear Dimensionality Reduction. The other is Nonlinear Dimensionality Reduction. In fact, the Linear Dimensionality Reduction is based on the different criterision of optimization and to seek the optimal linear model. This is totally different from the Nonlinear Dimensionality Reduction. However, the data of the practical application is usually not the linear combination within features. Consequently, it triggered the study of the manifold learning in the field of the nonlinear dimensionality reduction.
The manifold learning method commonly can be divided into three categories. These three categories are the global comparison of the linear model, the nonlinear method of preserving local property and the nonlinear method of preserving global property. The method of the global comparison of the linear model majorly refers to LLC. While the nonlinear method of preserving local property includes LLE, Hessian LLE, Palladian Eigen map and LTSA. The nonlinear method of preserving global property involves the nonlinear dimension reduction of the multidimensional scaling of based on kernel (Kernel PCA, Fisher Analysis), Isomap and Diffusion map so on. The main differences between the global method and the local method lie in the local structure and the way of embedding.
The dimension reduction method was widely welcomed in many fields since it was proposed. These fields are the face recognition field and cluster analysis field so on. Over the past years, the dimension reduction method has been improved. However, there are some limitations in reality. These limitations especially presented in the manifold method.
The first limitation is that it is difficult to obtain the mapping relationship from the high-dimensional space to the low-dimensional space during the process of dimensionality reduction.
The second limitation is the dimension reduction problem of processing dimension jump.
Thirdly, it is difficult to get an effective study method of the manifold as the data collection is relatively sparse.
Finally, it is lack of the studies in improving the efficiency of handling large amounts of data after the combination of the manifold algorithm and parallel computing.
Cite this paper
Lan Fu, (2015) The Discriminate Analysis and Dimension Reduction Methods of High Dimension. Open Journal of Social Sciences,03,7-13. doi: 10.4236/jss.2015.33002
References
- 1. Donoho, L. (2000) High Dimensional Data Analysis: the Curses and Blessings of Dimensionality. Present Data American Mathematics Society Conference.
- 2. Lu, T. (2005) Dimension Reduction Theory and Application of the High Dimensional Data. 5-31, 59-96.
- 3. XiaoSheng, Y. and Ning, Z. (2007) The Method Research of the Dimension Reduction. Information Science 8th.
- 4. SongCan, C. and DaoQiang, Z. (2009) The dimension Reduction of the High Dimensional Data. China Computer Federation Information 8th.
- 5. Fan, J.Q. and Fan, Y.Y. (2008) High Dimensional Classification Using Features Annealed Independent Rules. Annals of Statistics, January 23.
- 6. Van der Maaten (2009) Dimensionality Reduction: A Comparative Review. Journal of Machine, 1-22.
- 7. Demers, D. and Cottrell, G. Non-Linear Dimensionality Reduction. Dept. of Computer Science & Engr, September, 67.
- 8. ZhongBao, L., Guangzhou, P. and WengJuan, Z. (2013) The Manifold Discriminate Analysis. Journal of Electronics & Information Technology 9th.
- 9. DeWeng, H., JianZhou, X., JunSong, Y. and Tan, Z. (2007) The Analysis and Application of the Nonlinear Manifold Learning. Progress in Natural Science 8th.
- 10. Wood, F. (2009) Principal Component Analysis. December 68.
- 11. Ma, R., Song, Y.X. and Wang, J.X. (2008) Multi-Manifold Learning Using Locally Linear Embedding Nonlinear Dimensionality Reduction. Journal of Tsinghua University, 582-589.
- 12. Roweisst, S. (2000) Nonlinear Dimensionality Reduction by Locally Linear Embedding. Science, December 22.


