Received February 2015

ABSTRACT

A quasi-optical dielectric lens used for W-band focal plane array passive imaging has been developed. The imaging system requires the lens to form beam spot with 3 dB width less than 35 mm at distance of 3500 mm. The powerful optical design software ZEMAX was utilized to design the contours of the lens, and numerical method based on ray tracing and Huygens’ Principle was pro- cessed to verify the design result. Measurement result shows that the 3 dB width of the beam spot formed by the lens is 34 mm at distance of 3460 mm, and the beam pattern on imaging plane are equally arranged and the intensity decreases only 0.55 dB while the object lateral deviation increases to 300 mm.

Keywords:

Quasi-Optical Lens, Passive Millimeter-Wave Imaging, Numerical Method, Huygens’ Principle

1. Introduction

Security checks are getting more and more common in peoples life nowadays. Security devices that can see through passenger’s clothing and inspect carrying contraband are needed in airplanes, schools, and other sensitive areas.

According to black-body radiation theory, all natural materials always radiate the thermal radiation in MMW range, and its radiation power intensity depends on the emissivity and the physical temperature of the object. Since millimeter wave (MMW) can penetrate clothing, fogs, clouds, smoke and other nonmetallic materials with little losses, image of concealed objects in clothes can be obtained by using PMMW imaging camera [1] [2].

PMMW imaging camera forms image by collecting the electromagnetic power emitted by objects in its field of view, which corresponding to intensity distribution of MM-wave radiation. Therefore it can detect and locate concealed metallic, ceramic and plastic objects through clothing in a noninvasive and noncontact manner [3] [4].

In a PMMW imaging system, quasi-optical lens concentrates the received MMW power on its imaging plane where the receiver array is located [2]. The main characteristics of PMMW imaging system, including the field of view (FOV), the spatial resolution (SR) and the thermal sensitivity are mainly decided by the quasi-optical lens [5]. The angle scanning ability of the lens decides the FOV of the system, and the spot size formed by lens decides the SR of the system, and the efficiency of the lens affects greatly the thermal sensitivity of the system. Other characteristics of the lens, such as depth of focus (DOF), are also critical for PMMW imaging.

Many authors have demonstrated their design theories and experiment results of lens antenna for various applications [6] [7]. In this paper, the design of a W-band quasi optical lens antenna for short-range passive imaging is presented. The optimized contour of the lens is obtained by optical method first, then numerical simulation based on method of electromagnetic fields is processed to verify the design, finally the lens is fabricated and its main characteristics are tested.

2.1. Design of W-Band Quasi-Optical Lens

The lens antenna is used for 89 GHz PMMW imaging camera used for security checks. General required characteristics of the camera include: 1) imaging at frame rate not less than 2 Hz with 700 mm * 1800 mm filed of view; 2) spatial resolution of images better than 35 mm with a distance of 3 m .

Utilization of two-dimensional (2-D) imaging sensor array placed on focal plane can obtain a frame rate as high as 25 Hz. However, the number of imaging sensors will be multiple count even decuple, that means the cost of the 2-D system will increase greatly. As a compromise, 1-D imaging sensor array combined with a flapping reflector is employed.

2.2. Scheme of the Optical System

The scheme of the optical system is shown in Figure 1. The lens lies horizontally, and 20 imaging sensors are arranged on its focal plane. The flapping reflector is located between lens and imaging targets. Comparing with the situation that flapping reflector located between the lens and the imaging sensor array, such an arrangement will reduce the scan angle of the flapping reflector by half. In fact, to cover a area of 700 mm * 1800 mm with a distance of 3 m, the scan angle range of the flapping reflector is only about 20˚.

2.3. Formulas for Lens Design

The Gaussian lens equation is given as follows

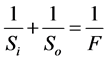(1)

where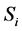, 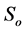and are the image distance, the object distance and the focal length of lens. According to the Rayleigh criterion, the spatial resolution of the lens is given by

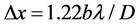(2)

where b is the distance between lens and image plane, and λ is the wavelength and D is diameter of lens. The corresponding spatial resolution on object plane is

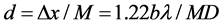(3)

where is the magnification of the lens, and d is also the 3 dB beam spot size of the lens.

Required by sampling theorem, the imaging sensors need to be closed packed. So the size of imaging sensor should be less than. However, small aperture size of the sensor results in a broad beam illuminating the lens, and that will much reduce efficiency of the antenna. Therefore, 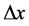must be chosen appropriately.

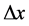By choosing D = 430 mm, b = 585 mm, = 3.37 mm, S_i = 600 mm and S_o = 3500 mm, we can get = 5.6 mm and the spatial resolution d = 32.7 mm from (2), (3). The value of S_o is larger than 3000 mm because part of the optical path is contained inside the imaging system.

To keep the beam quality from the aberration, aspheric bi-convex surfaces have been chosen for the lens. The design formula of the contour is shown as follow:

(4)

where y and z are the design coordinates, and a, b, c, d, e, R and k are the parameters for both surfaces. The lens is made of high density polythene (HDPE) with a relative permittivity of 2.3.

2.4. Numeric Analysis of the Lens

The values of R, k, a, b, c, d, e determine the contour of the lens. These parameters were optimized to achieve low spherical aberration by using the powerful optical design tool ZEMAX. ZEMAX is designed based on optical method, so its accuracy will decrease when it is used to design quasi-optical lens. So numeric method based on ray tracing and Huygens’ Principle was adopted to calculate the near field of the lens. This method has proven to be effective for lens designing [8].

In this method, the radiated field of the feed was calculated with HFSS software first. The feed is a pyramidal horn with a aperture size of 8 mm * 5.5 mm. The aperture of the horn is meshed with triangles, and then the E and H field at all nodes of the triangles are calculated by HFSS. Then the field on the illuminated surface of the lens is calculated by aperture field integration method with the E and H. Next the field on second surface of the lens will be obtained by calculating the field transferring through the lens using ray tracing method. Finally, the output filed at any point in the near field region of the lens can be calculated with Stratton-Chu formula:

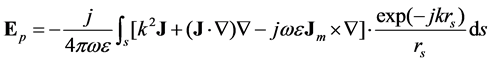(5)

in which,

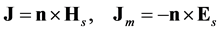(6)

where s denotes the total second surface of lens, , are the electric and magnetic field on the surface, is the unit normal vector of surface of the lens, and r_s is the distance between source point and field point. Formula (5) can be expressed in form as follow:

(7)

in which,

(8)

(9)

(10)

After the optimized values of R, k, a, b, c, d and e were obtained by ZEMAX, the shape of the lens was determined according to Formula (4). Then numeric calculation was processed and the field distribution in the near field region of the lens was calculated. Numeric result showed that object distance of the lens would be smaller than the value given by ZEMAX. For example, for lens optimized by ZEMAX with S_o = 3500 mm and S_i = 600 mm, its calculated S_o was about 3284 mm. The final lens was optimized with S_o = 3780 mm, while numeric calculation showed its S_o was 3520 mm. The parameter values of the contours of the bi-convex lens were given in Table 1, and the ray tracing result was shown in Figure 2.

3. Measurement Result

3.1. Measurement System

The quasi-optical dielectric lens antenna was fabricated and measured. The lens and the measurement system are shown in Figure 3.

A pyramidal horn connected with W-band source is applied as a transmitter. The aperture size of the horn is 8 mm * 5.5 mm, and its gain is 15.4 dB and −10 dB beam width is 53˚. The position of the transmitter is tunable axially and laterally. The receiving antenna is a standard horn antenna with 25 dB gain. The received power is down-converted and delivered to a spectrum analyzer to measure the power. The receiver is mounted on a sliding rail, and it can be shifted axially and laterally too.

3.2. Result and Analysis

To test the effective focal length of the lens, the S_i and S_o was measured first. By fixing the receiver at object distance, S_o = 3500 mm, and scanning the transmitter on the optical axis by step of 1 mm, the optimum image distance would be obtained when the maximum output power of the receiver was observed. The measured optimum S_i was 576 mm for S_o = 3500 mm. Thus the effective focal length, F, of about 495 mm can be calculated according to Formula (1).

Locating the transmitter at the S_i = 576 mm, the electric field distribution along the optical axis was measured by scanning the receiver axially by step of 5 mm. The measurement result is shown in Figure 4. It can be found that the max power level occurs at 3460 mm, and that means the best focus point locates at that position.

The beam spot at the best focus point was measured by scanning the receiver laterally. The measured 3 dB beam width of the spot is about 34 mm, slightly larger than the theoretical value of 32.7 mm, as shown in Figure 5.

The measured beam patterns on the image plane are shown in Figure 6. Locating the receiver on object plane at S_o = 3460 mm with lateral deviations of 0 cm, 3 cm, 6 cm ・・・ 30 cm respectively, the beam patterns were obtained by scanning the transmitter laterally by step of 1 mm on the image plane. It can be seen that the beam patterns are equally arranged. With object deviation increasing from 0 cm to 30 cm, the power intensity decreases 0.55 dB and the 3 dB beam widths increase from about 5 mm to 5.5 mm due to aberration. Since the actual magnification M is about 6.01, larger than the theoretical value of 5.83, the average beam interval decreases to 5.2 mm, smaller than the theoretical value of 5.6 mm.

4. Conclusion

Quasi-optical lens antenna used for W-band passive millimeter wave imaging has been developed. The contours of lens are optimized with optical design tool. Numerical method based on ray tracing and Huygens’ Principle is employed to examine whether the design is proper. Numerical calculation shows that actual object distance of quasi-optical lens will be smaller than the result obtained with ZEMAX. Experimental results are in good

agreement with numeric result. The lens has good beam patterns uniformity in field of view, so it is suitable for the application of focal plane array.

Cite this paper

Qike Chen,Yong Fan,Jingshi Zhou,Kaijun Song, (2015) Design of Quasi-Optical Lens Antenna for W-Band Short Range Passive Millimeter-Wave Imaging. Journal of Computer and Communications,03,93-99. doi: 10.4236/jcc.2015.33016

References