Journal of Computer and Communications
Vol.03 No.03(2015), Article ID:54690,5 pages
10.4236/jcc.2015.33002
Minimal Generalized Time-Bandwidth Product Method for Estimating the Optimum Fractional Fourier Order
Lin Tian1,2, Zhenming Peng1
1School of Optoelectronic Information, University of Electronic Science and Technology of China, Chengdu, China
2Department of Electronics and Information Engineering, Yili Normal University, Yili, China
Email: tianlin20110501@163.com, zmpeng@uestc.edu.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received November 2014

ABSTRACT
A minimal generalized time-bandwidth product-based coarse-to-fine strategy is proposed with one novel ideas highlighted: adopting a coarse-to-fine strategy to speed up the searching process. The simulation results on synthetic and real signals show the validity of the proposed method.
Keywords:
Generalized Time-Bandwidth Product, Coarse-to-Fine Strategy, Optimum Fractional Fourier Order, Fractional Fourier Transform

1. Introduction
To get a high resolution time-frequency distribution, fractional Fourier transform (FrFT) is a useful tool. Traditional time-frequency method combined FrFT, and fractional Gabor transform was proposed [1]-[3], the optimum order of FrFT is major factor of the transform, for it determines the appropriate fractional domain where the signal is best concentrated. In [2] the optimum order of FrFT is chosen by the chirp rate of the signal. This transform can get high resolutions, yet the time-frequency distributions are in time-fractional plane, the physics meaning is not clean. In [4] Wigner distribution function and its FrFT are used to get high resolutions results, using FrFT, and inverse FrFT, the physics meaning is clean, and Wigner distribution function and its FrFT were used to estimate the optimum order, yet the method is not appropriate for a lot of time-frequency components. The fractional optimal short-time Fourier transform was proposed [5], this method utilizes the FrFT to improve the resolution of the time-frequency distributions, and the generalized time-bandwidth product (GTPB) was proposed. In [6] the fractional Gabor transform was proposed which has clean physics meaning, to save computational cost, the maximal amplitude in fractional domain was used for optimum fractional Fourier order in the paper. The fast algorithm of maximal amplitude has established in fractional domain [7]. For FrFT can be interpreted as a decomposition of the signal in terms of chirps, this method is appropriate for signal detection [8]. For non-stationary signal time-frequency analysis, the optimum order of FrFT can be found the minimal generalized time-bandwidth product. This method is suitable for signal which has many components or has continuous spectra. However, the minimal generalized time-bandwidth product can give the directly optimum order. Since there is no fast algorithm, this paper uses coarse-to-fine strategy, and gives a fast algorithm. Though, theoretically, the amplitudes-based method is fast, it is powerless for the signals to consist many components in time-frequency analysis. We propose a minimal-generalized time-bandwidth product-based coarse-to-fine algorithm to estimate the compact fractional domain in this paper.
2. Minimal Generalized Time-Bandwidth Product Method
2.1. Generalized Time-Bandwidth Product
Fractional Fourier transform (FrFT) is a generalization of the Fourier transform, FrFT is a linear operator. The FrFT of signal can be interpreted as the rotating the signal in the time-frequency plane, the FrFT of  is defined as [9]:
is defined as [9]:
 (1)
(1)
where  is the p-th order FrFT of
is the p-th order FrFT of , p is the transform order of FrFT, the period of p is 4.
, p is the transform order of FrFT, the period of p is 4.  is an operator, means the r-th order FrFT.
is an operator, means the r-th order FrFT. 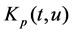 is the transform kernel which is given as follows [10]:
is the transform kernel which is given as follows [10]:
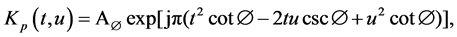
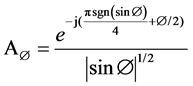 (2)
(2)
where 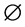 is rotation angle in time-frequency plane, and
is rotation angle in time-frequency plane, and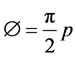 .
.
In light of the properties of the FrFT, the interval of the optimum order can be restricted in [0, 2) [11]. The time-bandwidth product (TBP) of the signal 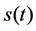 of the weighted window function is defined as follows [6]:
of the weighted window function is defined as follows [6]:
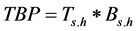 (3)
(3)
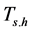 and
and  represent the time and the frequency width of the signal of the weighted window function, respectively.
represent the time and the frequency width of the signal of the weighted window function, respectively.
If the p-th order FrFT of signal 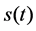 is
is 


where 





where 





where 








where 





where 







2.2. Optimum Order of FrFT Estimated by GTBP
The optimum order of FrFT can be given by minimal generalized time-bandwidth product:

According to the operation properties of FrFT, the order of FrFT can be narrowed to the range of 

2.3. Algorithm of MGTBP
Suppose 
Step 1:


Step 2: let
Step 3: perform FrFT of the signal for each
Step 4: Find 
Step 5:


The above loops can be stopped until the number of cycles equals to the number M:

where 
Figure 1 shows the main idea of such coarse-to-fine of the general time-bandwidth product (GTBP). At the beginning, GTBP is computed for different values of order of FrFT that are distributed over the interval [0, 2], and the optimum order is roughly fund. Then a finer searching will be done on a small interval around the optimum order. This procedure will be repeated until the obtained satisfies the predefined accuracy requirement.
2.4. Computational Complexity of MGTBP
Suppose an N points signal 









3. Simulation Results and Analysis
The MGTBP is implemented for searching the optimum order of FrFT, the fast discrete FrFT algorithm is reported by Ozakatas et al. [10]. The method proposed in our paper is compared with the MACF method [8]. First, A signal is used to evaluate the synthetic signal consisting of two attenuated chirp components, the signal can be written as the following formula:
The parameter settings take the values as follows:

4. Discussion and Conclusions
In this paper, the MGTBP method for estimating the optimum fractional Fourier order has been developed. Its computational complexity is

Figure 1. Schematic showing the stream of the coarse-to-fine procedure.

Figure 2. Fractional Gabor transform at different optimum order. (a) 0-th order as optimum order given by MACF; (b) 0.737-th order as optimum order given by MGTBP.
Acknowledgements
The authors wish to thank the National Natural Science Foundation of China (Grants No. 41274127) and the Yili Normal University research project (Grants No. 2014YSYB04) for financial support of this research.
Cite this paper
Lin Tian,Zhenming Peng, (2015) Minimal Generalized Time-Bandwidth Product Method for Estimating the Optimum Fractional Fourier Order. Journal of Computer and Communications,03,8-12. doi: 10.4236/jcc.2015.33002
References
- 1. Akan, A., Shakhmurov, V. and Cekic, Y. (2001) A Fractional Gabor Transform. IEEE International Conference on Acoustics, Speech, and Signal Processing, (ICASSP'01), Salt Lake City, 7-11 May 2001, Vol. 6, 3529-3532.
- 2. Zhang, Y., Gu, B.Y., Dong, B.Z., et al. (1997) Fractional Gabor Transform. Optics Letters, 22, 1583-1585. http://dx.doi.org/10.1364/OL.22.001583
- 3. Akan, A. and Çekiç, Y. (2003) A Fractional Gabor Expansion. Journal of the Franklin Institute, 340, 391-397. http://dx.doi.org/10.1016/j.jfranklin.2003.08.004
- 4. Pei, S.C. and Ding, J.J. (2007) Relations between Gabor Transforms and Fractional Fourier Transforms and Their Applications for Signal Processing. IEEE Transactions on Signal Processing, 55, 4839-4850. http://dx.doi.org/10.1109/TSP.2007.896271
- 5. Durak, L. and Arikan, O. (2003) Short-Time Fourier Transform: Two Fundamental Properties and an Optimal Implementation. IEEE Transactions on Signal Processing, 51, 1231-1242. http://dx.doi.org/10.1109/TSP.2003.810293
- 6. Chen, Y.P., Peng, Z.M., He, Z.H., Tian, L. and Zhang, D.J. (2013) The Optimal Fractional Gabor Transform Based on the Adaptive Window Function and Its Application. Applied Geo-physics, 10, 305-313. http://dx.doi.org/10.1007/s11770-013-0392-2
- 7. Zheng, L. and Shi, D. (2010) Maximum Amplitude Method for Estimating Compact Fractional Fourier Domain. IEEE Signal Processing Letters, 17, 293-296. http://dx.doi.org/10.1109/LSP.2009.2038511
- 8. Guan, J., Chen, X.L., Huang, Y. and He, Y. (2012) Adaptive Fractional Fourier Transform-Based Detection Algorithm for Moving Target in Heavy Sea Clutter. IET Radar, Sonar and Navigation, 6, 389-401. http://dx.doi.org/10.1049/iet-rsn.2011.0030
- 9. Almeida, L.B. (1994) The Fractional Fourier Transform and Time-Frequency Representations. IEEE Transactions on Signal Processing, 42, 3084-3091. http://dx.doi.org/10.1109/78.330368
- 10. Ozaktas, H.M., et al. (1996) Digital Computation of the Fractional Fourier Transform. IEEE Transactions on Signal Processing, 44, 2141-2150. http://dx.doi.org/10.1109/78.536672
- 11. Tian, L. and Peng, Z. (2014) Determining the optimal Order of Fractional Gabor Transform Based on Kurtosis Maximization and Its Application. Journal of Applied Geophysics, 108, 152-158. http://dx.doi.org/10.1016/j.jappgeo.2014.06.009






