Journal of Computer and Communications
Vol.03 No.03(2015), Article ID:54689,7 pages
10.4236/jcc.2015.33001
Face Recognition Using Fuzzy Clustering and Kernel Least Square
Essam Al Daoud
Computer Science Department, Zarqa Private University, Zarqa, Jordan
Email: essamdz@zpu.edu.jo
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received October 2014

ABSTRACT
Over the last fifteen years, face recognition has become a popular area of research in image analysis and one of the most successful applications of machine learning and understanding. To enhance the classification rate of the image recognition, several techniques are introduced, modified and combined. The suggested model extracts the features using Fourier-Gabor filter, selects the best features using signal to noise ratio, deletes or modifies anomalous images using fuzzy c-mean clustering, uses kernel least square and optimizes it by using wild dog pack optimization. To compare the suggested method with the previous methods, four datasets are used. The results indicate that the suggested methods without fuzzy clustering and with fuzzy clustering outperform state- of-art methods for all datasets.
Keywords:
Face Recognition, Fuzzy Clustering, Kernel, Least Square, Gabor Filters

1. Introduction
Facial recognition has been an active research topic since the early nineties. There have been several advances in the past few years in terms of face detection and tracking, feature extraction mechanisms and the related machine learning techniques. Face recognition has drawn the attention of researchers in fields from image analysis and processing, computer vision, to psychology and security [1]. In spite of more than fifteen years of extensive re-search, large number of papers published in journals and conferences dedicated to this area, we still cannot claim that automatic face recognition is comparable to human performance [2]. The difficulty of automatic face recognition is due to various effects like aging, facial expressions, occlusions, lighting and viewpoint changes induced by body movement [3]. A successful face recognition mythology depends heavily on the particular choice of the features, observation reduction and classification method. In this paper four algorithms have introduced, modified and combined to enhance the face recognition and detection [4]. The features are extracted using Fourier-Gabor filter and selected by generalizing signal to noise equation. Modified fuzzy clustering algorithm is used to reduce the misclassified faces by excluding or modifying the low membership faces. Furthermore a new non-linear kernel is used to kernel the least square method and the wild dog pack optimization is implemented to find the optimal parameters. The suggested method is implemented by using four datasets: AT & T database of faces (ATT), Indian Face Database (IFD), Faces95 from Essex university database and Yale face database (Yale).
2. Previous Studies
Principal component analysis (PCA) converts a set of faces images of possibly correlated variables into a set of values of linearly uncorrelated variables called principal components. PCA can be used to capture as much as possible of the variability of the face image where the eigenfaces matrix can be used to recognize the new faces by minimizing [5]:
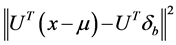 (1)
(1)
where U is the eigenfaces matrix or features matrix, 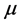 is the mean image and
is the mean image and 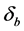 is the difference between the input image xb and the mean. Linear discriminant analysis (LDA) selects eigenvectors U in such a way that the ratio of the between-class scatter and the within class scatter is maximized which characterizes or separates two or more classes of faces images
is the difference between the input image xb and the mean. Linear discriminant analysis (LDA) selects eigenvectors U in such a way that the ratio of the between-class scatter and the within class scatter is maximized which characterizes or separates two or more classes of faces images
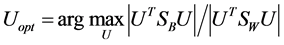 (2)
(2)
where SB and SW are the between class scatter matrix and the within class scatter matrix respectively and Uopt can be found by solving the generalized eigenvalue problem [6]. Independent component analysis (ICA) separates a multivariate signal into additive subcomponents. ICA uses centering, whitening, and dimensionality reduction as preprocessing steps in order to simplify and reduce the complexity of the problem for the actual iterative algorithm [7]. The whitening matrix is twice the inverse square root of the covariance matrix, this removes the first and the second-order statistics of the data [8]. Fourier transform is another important method, which plays a critical role in a broad range of image processing applications. The output of the transformation represents the image in the Fourier or frequency domain, while the input image is the spatial domain equivalent. For a square image of size n × n, the two-dimensional DFT for the point a and b in spatial domain is equivalent to the point m and n in frequency domain, this transform can be calculated as following:
Fourier (m, n, imgA) = 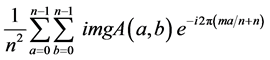 (3)
(3)
Gabor filters have been used to solve the configuration, orientations and emotions problems. A filter bank consisting of Gabor filters with various scales and rotations can be created and combined with different methods to enhance the recognition rate. The most commonly used filter in face recognition have the form [9]:
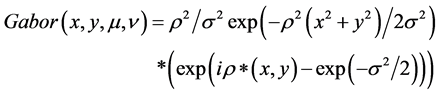 (4)
(4)
where
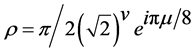 (5)
(5)
The output locations for each Gabor sub-matrix are specified by x and y. 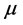 and
and 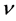 define the orientation and scale of each sub-matrix.
define the orientation and scale of each sub-matrix.
3. The Suggested Method
The suggested method modifies and combines several techniques to enhance the face recognition. The main steps can be summarized as following:
1) Extract features from each image using Fourier-Gabor filte
2) Select the best features using signal to noise ratio (SNR)
3) Delete or modify anomalous images using fuzzy c-mean cluster
4) Model the training images using the least square method
5) Use a new non linear kernel
6) Optimize the weight vector using wild dog pack optimization (WDPO)
3.1. Feature Extraction and Selection
There are several methods have been used to extract the features from the face images, one among the best methods is Fourier-Gabor filter which is introduced in [8]. Therefore the same method will be used in this study to extract the features from the face images. However different size, orientation and scale values are adopted in this study. The main steps are as following:
1) Resize the images to 40 × 40
2) Transform the images to frequency domain by applying Fourier transform in Equation (3)
3) Use Equation (4) to prepare 8 Gabor filters for orientation and 10 filters for scaling. Thus 80 different filters will be constructed
4) Multiply the result matrix in step 2 by each matrix in step 3.
5) Resize each matrix in step 4 as one row
6) Construct the feature vector for each face by concatenation all the rows in step 5.
The number of the extracted features is 40 × 40 × 80 = 104,000. To delete insignificant features, Signal-to- Noise Ratio (SNR) method is applied [10]:
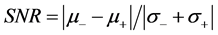 (6)
(6)
where 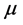 is the mean,
is the mean, 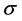 is the standard deviation and the signs {+, −} are indicate to the class. But for multiclass, as in our case, one against all procedure is repeated for all classes and the total is calculated. The features that have lowest total are deleted.
is the standard deviation and the signs {+, −} are indicate to the class. But for multiclass, as in our case, one against all procedure is repeated for all classes and the total is calculated. The features that have lowest total are deleted.
3.2. Face Reduction and Modification
If face x in a class is closer to the faces in another class, this will lead to misclassification of the new faces that are close to the face x. Therefore, fuzzy clustering is used to modify the faces that have low membership degree in the correct class and delete the faces that have high membership degree in the wrong classes. Thus the fuzzy c-mean clustering will be modified as following:
1) Initialize the membership randomly 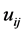
2) Calculate the centers
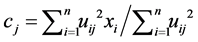 (7)
(7)
3) Update the memberships
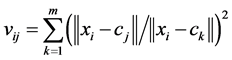 (8)
(8)

4) Go to step 2 until no significant improvement.
5) For all 
Consider 
If 
Delete 
If 
Modify
6) Go to step 2 until the above conditions become invalid.


3.3. Kernel Least Square Method
Once the features and the observations have prepared, several classifiers can be used such as neural networks, support vector machine (SVM) and regularized least squares classification (RLSC) [10]. In this section RLSC will be used with a new non linear kernel and will be minimized by wild dog packs optimizer (WDPO). The general formulization of non-linear regularized least squares classification as following:

w is the weight vector, y is the target class, 

To train RLSC the parameters 

Algorithm 1: Wild dog pack optimization (WDPO) Generate n dogs randomly
while (t < iter)
Evaluate Locations using the updated parameters
Choose the best location as alpha
Every few iterations update the parameters using self competition
Update the dogs locations with regard to alpha using Equation (12):

c: is used to control the diversity from alpha
Evaluate dogs
Choose the best dog as alpha
If no improvement for v iterations
Use Hoo procedure to escape from the local minimum
4. Experimental Results
In this study four datasets are used: AT & T database of faces (ATT), Indian Face Database (IFD), Faces95 from Essex university database and Yale face database (Yale) [13]-[16]. Figure 1 show samples faces from each dataset. All the datasets have many subjects and several images per individual, different facial expressions, configuration, orientations and emotions are used. Table 1 summarizes the content of each dataset.
Figure 1. Faces from ATT, Yale, IFD and Faces95.
All the results in this section are found by using 10-fold cross validations. The code is written by using Matlab 10. The experiments are divided into three stages. The first stage is used to find the best number of features using signal to noise method. The implementation in this stage is repeated several times, each time the number of the features is reduced by 10,000. Table 2 shows sample results of different number of features. The best number of the features according to this stage is 80,000. The second stage is to find the best values of the clustering parameters s and r. Table 3 indicates that the best values are s = 50 and r = 30. The third stage is to compare the proposed method with three famous methods: Linear discriminant analysis (LDA), Principal component analysis (PCA), and Gabor-SVM. Moreover, to the proposed method is implemented with and without fuzzy clustering. Table 4, Table 5 show the classification rate using 30% and 50% for training respectively. The results indicate to that the suggested methods without fuzzy clustering and with fuzzy clustering outperform state-of-art methods for all datasets.
Table 1. Face dataset description.
Table 2. Sample results by using different number of features.
Table 3. Sample results by using different values for the clustering parameters s and r.
Table 4. The classification rate using 30% for training.
Table 5. The classification rate using 50% for training.
5. Conclusion
Face recognition presents a challenging problem in the field of image analysis and computer vision, and as such has received a great deal of attention over the last few years because of its many applications in various domains. The performance of the proposed method was demonstrated on various datasets that contain several images per individual, different facial expressions, configuration, orientations and emotions. The results are quite promising; the suggested method outperforms the previous methods for all datasets. The future work will be dedicated to apply and combine the other features that are extracted by various techniques.
Cite this paper
Essam Al Daoud, (2015) Face Recognition Using Fuzzy Clustering and Kernel Least Square. Journal of Computer and Communications,03,1-7. doi: 10.4236/jcc.2015.33001
References
- 1. Zeng, Z., Pantic, M., Roisman, G.I. and Huang, T.S. (2009) A Survey of Affect Recognition Methods: Audio, Visual, and Spontaneous Expressions. IEEE Trans. Pattern Analysis and Machine Intelligence, 31, 39-58. http://dx.doi.org/10.1109/TPAMI.2008.52
- 2. Aleksic, P.S. and Katsaggelos, A.K. (2006) Automatic Facial Expression Recognition Using Facial Animation Parameters and Multistream HMMs. IEEE Trans. Information Forensics and Security, 1, 3-11. http://dx.doi.org/10.1109/TIFS.2005.863510
- 3. Kotsia, I. and Pitas, I. (2007) Facial Expression Recognition in Image Sequences Using Geometric Deformation Features and Support Vector Machines. IEEE Trans. Image Processing, 16, 172-187. http://dx.doi.org/10.1109/TIP.2006.884954
- 4. Kotsia, I., Buciu, I. and Pitas, I. (2008) An Analysis of Facial Expres-sion Recognition under Partial Facial Image Occlusion. Image and Vision Computing, 26, 1052-1067. http://dx.doi.org/10.1016/j.imavis.2007.11.004
- 5. Sahoolizadeh, A.H., Heidari, B.Z. and Dehghani, C. (2008) A New Face Recognition Method Using PCA, LDA and Neural Network. Proceedings of World Academy of Science En-gineering and Technology, 31, 7-12.
- 6. Pang, S., Ozawa, S. and Kasabov, N. (2005) Incremental Linear Discriminant Analysis for Classification of Data Streams. IEEE Transactions on Systems, Man, and Cybernetics, Part B, 35, 905-914. http://dx.doi.org/10.1109/TSMCB.2005.847744
- 7. Bartlett, M.S., Movellan, J.R. and Sejnowski, T.J. (2002) Face Recognition by Independent Component Analysis. IEEE Transaction on Neural Networks, 13, 1450-1462. http://dx.doi.org/10.1109/TNN.2002.804287
- 8. Al Daoud, E. (2009) Enhancement of the Face Recognition Using a Modified Fourier-Gabor Filter. Int. J. Advance. Soft Comput. Appl., 1, 119-131.
- 9. Vukadinovic, D. and Pantic, M. (2008) Fully Automatic Facial Feature Point Detection Using Gabor Feature Based Boosted Classifiers. IEEE Interna-tional Conference on Systems, Man and Cybernetics Waikoloa, Hawaii, 10-12 October 2005, 1692-1698.
- 10. Hastie, T., Tibshirani, R. and Friedman, J. (2009) The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2nd Edition, Springer, New York. http://dx.doi.org/10.1007/978-0-387-84858-7
- 11. Wang, X.Y. and Garibaldi, J.M. (2005) Simulated Annealing Fuzzy Clustering in Cancer Diagnosis. Informatica, 29, 61-70.
- 12. Al daoud, E., Alshorman, R. and Hanandeh, F. (2014) A New Efficient Meta-Heuristic Optimization Algorithm Inspired by Wild Dog Packs. International Journal of Hybrid Information Technology, 7, 1-17.
- 13. AT & T. http://www.cl.cam.ac.uk/research/dtg/attarchive/facedatabase.html
- 14. Saha, K., Saha, P., Bhowmik, M.K., Bhatta-charjee, D. and Nasipuri, M. (2013) Creation of North-East Indian Face Database for Human Face Identification. Proc. SPIE 8659, Sensors, Cameras, and Systems for Industrial and Scientific Ap-plications XIV, Vol. 8659, 19 February 2013, 86590Q. http://dx.doi.org/10.1117/12.2002028
- 15. Faces95 from Essex University. http://dces.essex.ac.uk/mv/allfaces/
- 16. Yale Face Database. http://vision.ucsd.edu/content/yale-face-database







