Journal of Electronics Cooling and Thermal Control, 2011, 1, 1-13
doi:10.4236/jectc.2011.11001 Published Online June 2011 (http://www.SciRP.org/journal/jectc)
Enhancement of Heat Transfer Using Pins Swimming in
Non-Isothermal Fluidic Systems: Exact Solutions
Abdul Rahim A. Khaled
King Abdulaziz University, Thermal Engineering and Desalination
Technology Department, Saudi Arabia
Received April 27, 2011; revised June 20, 2011; accepted June 27, 2011
Abstract
Heat transfer to pins swimming in non-isothermal fluidic systems is theoretically analyzed. Four different
cases are considered: [A] pins aligned longitudinally in flowing fluid having constant temperature gradient,
[B] pins aligned transversely in flowing fluid flow with constant temperature gradient, [C] pins moving lon-
gitudinally towards a heated surface, and [D] pins moving transversely towards the heated surface. The Ap-
propriate unsteady energy transport equations are solved and closed form solutions for the fin temperatures
are obtained. Accordingly, different performance indicators are calculated. It is found that heat transfer to the
swimming pin increases as the pin thermal length, Peclet number and fluid temperature difference along the
pin length increase. It decreases as fluid temperature index along the motion direction increases. Moreover,
the swimming pins of case C are found to produce the maximum system effective thermal conductivity. In
addition, pins of case B with thermal lengths above 11 produce system thermal conductivity independent on
the thermal length. Meanwhile, pins of case A having thermal lengths above 10 produce system thermal
conductivities less responsive to the thermal length. The system thermal conductivity is noticed to increase
as the thermal length and Peclet number increase. Eventually, pins of case D produce system thermal con-
ductivities that are independent on the transverse temperature. Finally, the results of this work provide a ba-
sis for modeling super convective fluidic systems that can be used in cooling of electronic components.
Keywords: Conduction, Convection, Heat Transfer, Enhancement, Moving Pins
1. Introduction
Enhancing heat transfer in thermal systems becomes the
primary goal in thermal engineering. This goal can be
achieved by various means such as using fins [1-4] and
nanofluids [5]. Researchers succeeded to enhance the
heat transfer from the finned heated surfaces by several
means. For example, many fins configurations such as
the slit fins have produced heat transfer coefficient 50 to
100 percent above those of flat fins [6]. Moreover, Yang
et al. [7] succeeded to increase the heat transfer rate from
a fin-tube heat exchanger by 6.3 percent by optimizing
the fin spacing. Sahiti et al. [8] found out that employing
interrupted elliptic fins could produce heat transfer coef-
ficient 50 percent above that produced by interrupted
circular fins.
Almogbel and Bejan [9] and Almogbel [10] proved
that constructal optimization of a fin assembly is capable
of producing heat transfer coefficient 500 percent above
those of single fin under the same constraints. Li et al.
[11] showed that microfinnned helical tubes caused an
increase in the heat transfer by 120 percent compared to
that of plain tube. Kiwan and Al-Nimr [12] were among
the recent researchers who found that using a porous fin
with certain porosity might give same performance as
conventional fin and save 100 times porosity percent of
the fin material. Aldoss et al. [13] found out that the heat
transfer through a capsulated liquid metal fins might
reach about 500% above that of an equal-size steel fin.
Recently, Khaled [14,15] showed that heat transfer using
joint and permeable fins could be 100% and 40% above
that of typical flat fins, respectively. Moreover, Khaled
[16,17] showed that fins with roots and fins with internal
flows can increase heat transfer by about 100% and
200%, respectively, compared flat rootless fins.
Another recent method for enhancing the heat transfer

2 A. -R. A. KHALED
from the heated surfaces is by using nanofluids. These
are fluids containing suspensions of nanoparticles made
of high thermally conductive materials. Nanofluids are
noticed to possess large effective thermal conductivities
for very low concentrations of nanoparticles. For exam-
ple, the effective thermal conductivity of ethylene glycol
is increased by about 40% above that of the base fluid
when a 0.3% volume of copper nanoparticles of diame-
ters less than 10 nm are suspended in the fluid [18]. In
addition, Xuan and Li [19] showed that the convective
heat transfer coefficient was increased by 60% for nan-
ofluid composed of water and 2% Cu-nanoparticles by
volume. Finally, the estimated maximum levels of the
heat transfer enhancement due to different recent en-
hancing methods are summarized in the work of Man-
soor et al. [20]. Among these methods are utilizing (a)
fins and microfins, (b) porous media, (c) large particles
suspensions, (d) nanofluids, (e) phase-change devices, (f)
flexible seals, (g) flexible complex seals, (h) vortex gen-
erators, (i) protrusions, and (j) ultra high thermal conduc-
tivity composite materials.
From the previous brief literature survey, it is noticed
that many novel ideas were developed recently to en-
hance the heat transfer from the solid surfaces. In addi-
tion, it is proposed in the present work to consider high
thermally conductive pins submerged and swimming in
the fluid as a new novel method for enhancing the heat
transfer from the solid surface. The pin velocities are
considered different from the fluid velocity. It is referred
to these pins as to “swimming pins”. The resulting sol-
id-fluid system is different from the two-phase flow or
the nanofluid system [20] by having the pins moving at
constant or predetermined velocity. The velocity of the
swimming pins can be attained using different methods.
Among these methods are: 1) Applying appropriate
magnetic forces on the swimming pins along with using
magnetized pins, 2) Applying appropriate centrifugal
forces on the fluid/suspended-pins system, and 3) Ap-
pling appropriate electrostatic forces on the swimming
pins along with using electrically charged pins. To the
best author knowledge, this proposal has not been dis-
cussed before and it is though to be useful for cooling of
electronic components.
In this work, four different types of swimming pins are
theoretically analyzed. These are the following: [A] Pins
swimming longitudinally in flowing fluid having con-
stant temperature gradient, [B] Pins aligned transversely
and swimming in flowing fluid having constant tem-
perature gradient, [C] Pins swimming longitudinally to-
wards a heated surface, and [D] Pins moving transversely
towards the heated surface. Such these cases can form a
basis for constructing and modeling super convective
fluid/swimming-pins systems. Appropriate unsteady en-
ergy transport equations are identified and solved theo-
retically. Closed form solutions for the pin temperature
are obtained for each case. Accordingly, different pin
performance indicators and the effective thermal conduc-
tivity of the fluid/swimming-pins system are computed
for the studied cases.
2. Problem Formulation
2.1. Pins Swimming Longitudinally in Flowing
Fluid Having Constant Temperature
Gradient (Cases A)
Consider a pin having a uniform cross-sectional area AC
and a uniform perimeter P. This pin is suspended in
flowing fluid inside a heated pipe of diameter 2ro.
Moreover, the pin is considered to move inside the flow-
ing fluid at a constant velocity U. The pin length L which
is much larger than its characteristic transverse dimen-
sion LC = AC/P is taken for this case to be aligned along
the x'-direction as shown in Figure 1. Both x' and U have
the same direction. Let the pipe be subjected to constant
heat flux
s
q

 and the mass flow rate of the flowing fluid
be . As such, the surrounding fluid stream tempera-
ture d inside the pipe can be shown to be equal to the
following under fully developed condition:
m

T
 
,
so
ddi
p
qP
TxTx x
mc






 (1)
where Po, cp, ,di, x' and x are the pipe perimeter T


2π
o
Pro
, fluid specific heat, surrounding fluid stream
temperature at the inlet, distance between the inlet and
the pin left end and the pin coordinate starting from its
left end, respectively. The magnitude of x' is given by x' =
Ut where t is the time variable. The one-dimensional
energy equation applied to the pin can be written in the
following form:

2
2
f
fffff f
fd
ffC f
TcUT c
hP TT
kxkA k x

  T
t



 
 

  
(2)
where Tf,

f, cf, kf and h are the pin temperature, pin den-
sity, pin specific heat, pin thermal conductivity and the
convection heat transfer between the pin and the sur-
rounding fluid, respectively. Correlations for the
h-coefficient for each case with sufficient accuracy can
be obtained using any recent heat transfer textbooks [21].
Applying the following dimensionless variables:
*;
x
xL  (3a)
*;
Ut
tL  (3b)

A. -R. A. KHALED
3
Figure 1. Schematic diagram for swimming pins of cases: A and B, and the flow configurations with coordinates system.
,
f
d
di d
TT
TT


 (3c)
on Equation (2) will change it to the following dimen-
sionless form:

22
11
*2 *
1*
22
2
ff
ff
PemL Pe
xx
PePe t









 







(4)
where
f
Pe (pin Peclet number), m (pin index) and 1

(characteristic function) are given by
;
ff
ff
cUL
Pe k

 (5a)
;
f
C
hP
mkA  (5b)
1**
1
x
t
  (5c)
The pin is considered to be insulated from both left
and right ends. In addition, it is considered to be at tem-
perature ,
f
di when t = 0. As such, the dimen-
sionless boundaries and initial conditions are given by
TT

**
**
*
0,
0, 1;
xt
tx
x




*
t (6a)
 
**
**
*
1,
1
xt
tx
x





*
1,1;t

1
(6b)

**
,0xt   (6c)
The net heat transfer rate from the pin to the flowing
fluid,
f
d
q

, is given by


1
*
0
1
** *
0
d
d
fd d
so
p
qhPLTTx
qPL
hPLx tx
mc




 






(7)
The temperature increase across any pipe differential
element of thickness L which is denoted by
 TL is equal
to
L
so p
TqPLmc



. Define the dimensionless pin heat
transfer rate A as the ratio between the pin heat transfer
rate to that having maximum temperature difference of
 TL. Mathematically, it is equal to

1
** *
0
d
fd
AL
q
x
tx
hPL T


 
 (8)
Closed Form Solutions
Define the variable


**
,
g
xt as the following:



 
*** ***
,,
g
xtx txt   (9)
Substituting Equation (9) in Equation (4) results in the
following form of energy equation:

22
*2 **
2
fff
g
gg
PemL gPePe
x
xt





(10)
The boundaries and initial conditions are obtained by
substituting Equation (9) in Equations (6a-c). As such,
the boundary and initial conditions of

**
,

g
xt are giv-
en by

**
**
01
** *
1;
,0
xx
gg
xx
gxt x






(11a-c)

4

A. -R. A. KHALED
The solution of

**
,
g
xt can be decomposed into
sum of two solutions: 1) the steady state solution

*
sA
g
x and, 2) the homogenous solution


**
,
A
x
t  .
The corresponding governing equations for each one are
taken to be

22
*2 *
dd 2
dd
sA sA
fsA
gg
PemL gPe
xx
 0
f
 (12)

22
*2 **
AA
fA
PemLPe A
f
x
xt




 



(13)
The corresponding boundary and initial conditions are
taken to be
**
**
01
dd
1;
dd
sA sA
xx
gg
xx

 (14a)
** **
**
0, 1,
0;
AA
xt xt
xx







sA
(14b)
 
*** *
,0
A
x
txg   x
*
1
(14c)
Utilizing the theory of ordinary differential equations,
separation of variables and the Sturm-Liouville theory
[17], the following solutions can be obtained:
 
**
112 2
exp exp
sA
g
xC sxCsx A
(15)




2
** *
2
*
*22*
*
1
,exp
exp 4
exp π
2
Aa f
f
f
f
nn
nf
mL
xt Et
Pe
Pe mL t
Pe
Pe xnt
EX
Pe
















 






 


nx
(16)
where A1, C1, C2, s1 and s2 are equal to

12
2;
f
Pe
AmL  (17a)

  
2
1
12 1
exp1 ;
exp exp
s
Css s

 (17b)

  
1
2
22 1
1exp ;
exp exp
s
Css s

 (17c)

2
2
1;
24
ff
Pe Pe
s
mL  (17d)

2
2
224
ff
Pe Pe
s
mL (17e)
The functions


*
π
n
X
nx are equal to
 
**
πcos πsin π
2π
f
n
Pe

*
X
nx nxnx
n



 (18)
The constants Ea and En’s are equal to




1
2
1
11
exp 1
exp exp
exp 1
aff
fm
mf
mmf
f
EA
Pe Pe
Pes CPe
s
Pe
Pe























(19a)


2
2
22
22
22
2
2
2
122 22
exp1 1
2
1π
4 2π
2πexp1 1
2
ππ
42
n
f
n
f
n
f
mm m
mff
m
Pe
EPe n
n
Pe
nCs s
Pe Pe
ns n

























 



















 


(19b)
As such, the dimensionless heat transfer rate is equal
to
   



12
11 2
12
2
*
2
*
22*
2
122
1exp 1exp
exp
exp 4
exp1 1
2
π
exp
π
4
A
af
f
f
f
n
f
n
nff
CC
As s
ss
mL
EtPe
Pe
Pe mL t
Pe
Pe
nt
EPe Pe n


 



  







  










 











(20)
The maximum effective swimming pin index denoted
by m can be obtained by solving the following equation:
0.99
fd fd
mm m
qq




. As such, mL for this case is
obtained by solving the following equation:

 





2
**
sinh2 cosh0.01sinh
f*
s
Pesm Ls


(21)
where

2
*4
f
smLPe


2
. Note that the maximum
heat transfer rate is equal to

A. -R. A. KHALED
5
22
f
dfCLfffC
m
qkATPeLcA 
  L
UT .
2.2. Pins Aligned Transversely and Swimming
in Flowing Fluid Having Constant
Temperature Gradient (Cases B)
Let the pin described in section 2.1 be aligned trans-
versely such that the pin centerline is normal to the
U-direction as shown in Figure 1. The fluid temperature
around the pin can be approximated by the following
expression:

so
did p
qP x
Tx TTUt
Lmc



 



 (22)
where d is the fluid undisturbed stream temperature
increase across the pin length. Define the dimensionless
time according to the following:
T
*
2
f
ff
kt
tcL











(23)
According to Equation (23) and Equation (3a), Equa-
tion (22) changes to

*** *
,
didL
Txt T TxTPet f (24)
The one-dimensional energy equation applied to the
pin for this case has the following form:

2
2
f
ff f
fd
fC f
T
hP TT
kAk t
x

 


 
 

 
cT
(25)
Utilizing the dimensionless variables given by Equa-
tion (3a,c) and Equation (23), Equation (25) can be
changed to the following dimensionless form:

22
212
*2 **
2mL
x
xt











(26)
where 2

(characteristic function) and 1

(Tempera-
ture difference ratio) are given by
2**
1
1;
x
t
  (27a)
1
L
f
d
TPe
T

 



(27b)
The dimensionless boundaries and initial conditions as
adopted in section 2.1 can be expressed in the following
dimensionless forms:

**
**
1*
0,
0, 1;
xt
tx
x





 
**
**
1*
1,
1
xt
tx
x



*
1,1;t


 (28b)


**
,0xt  1
*
(28c)
The heat transfer from the pin to the flowing fluid is
given by


1
*
0
1
**
1
0
d
d
fd d
d
qhPLTTx
hPL Txtx 

 


(29)
Define the dimensionless pin heat transfer rate B as
the ratio between the pin heat transfer rate to that having
maximum temperature difference of . Mathemati-
cally, it is equal to
d
T

1
**
1
0
d
fd
Bd
q*
x
tx
hPL T


 
 (30)
Closed Form Solutions
Redefine the variable


**
,
g
xt as the following:



 
** **
1
,,
* *
g
xtx t xt   (31)
Substituting Equation (31) in Equation (25) results in
the following dimensionless form of the energy equation:

22
*2 *
f
g
g
mL gPe
x
t




 (32)
The boundaries and initial conditions are obtained by
substituting Equation (31) in Equations (28a-c). They are
given by Equations (11a-c). The equations for the steady
state and homogenous solutions are given by

22
*2
d0
d
sB sB
gmL g
x

 (33)

22
*2 *
B
B
B
mL
x
t







 (34)
The corresponding boundary and initial conditions are
given by Equations (14a-c). Utilizing the theory of ordi-
nary differential equations, separation of variables and
the Sturm-Liouville theory [22], the following solutions
can be obtained.




 
**
*coshcosh 1
sinh
sB
mLxmLx
gx mL mL



 (35)





2
***22* *
1
,exp expπcos π
Bn
n

x
tmLtFntn 


 
x
(36)
The coefficients Fn are equal to
 

222 22
11 11
2ππ
nn
n
FnmL n
 
 

 


 


 
 
(37)
*
t (28a)

6 A. -R. A. KHALED
As such, the dimensionless heat transfer rate is equal
to




2*22*
22
1
11
expexp π
π
n
Bn
n
mL tFntn






 



(38)
The steady state value of
B

is zero. According to
Equation (35), the pin base section is located at
where the convection heat transfer changes its direction
at this section. Therefore, the maximum conduction heat
transfer rate through this pin is obtained from the fol-
lowing mathematical relationship:
*0.5x

*
*
0.5
11
cosh 2
f
C
ff
x
C
fd
T
A
qk
Lx
A
kT
LmL



 



 



 


(39)
As such, the pin maximum dimensionless conduction
heat transfer denoted by
 is equal to
 
2
11
1cosh 2
f
d
q
hPL TmL
mL












(40)
The effective swimming pin length denoted by L can
be obtained by solving the following equation:
 
0.99
f
LL L
qq


f

. As such, mL can be shown
to be . 10.597mL
2.3. Pins Swimming Longitudinally Towards a
Heated Surface (Cases C)
Let the pin described in section 2.1 be moving towards a
hot surface with temperature Ts at a constant velocity U
as shown in Figure 2. The fluid stream temperature sur-
rounding the pin can be approximated by the following
expression:





exp
ds
TxTT Tbx x


 

(41)
where T

, b, x' and x are the fluid far stream temperature,
positive quantity, the position vector of the pin upper end
and the pin axial coordinate starting from the pin upper
end, respectively. The position vector x' is a time de-
pendent quantity given by x' = xo – Ut where t is the time
variable. In terms of dimensionless variables given by
Equation (3a,b), Equation (41) changes to




*** *
,exp
ds
TxtTT TCBxt
 
 
 

x
(42)
where B and C are equal to
;BbL (43a)

exp o Cb (43b)
According to Equation (41), the dimensionless time
Figure 2. Schematic diagram for swimming pins of cases: C
and D, and the flow configurations with coordinates system.
required for the pin to reach the heated surface is equal to
*1
fo
txL

. Redefining Equation (3c) as





** **
**
**
,,
,,
d
d
TxtT xt
xt TTxt 


 (44)
Applying the dimensionless variables given by Equa-
tion (3a,b) and Equation (44) on Equation (2) will
change it to the following dimensionless form:

2222
*2 *
*
22
2
ff
ff
PeBmLPe BBB
xx
BPePe t
 












(45)
The dimensionless boundaries and initial conditions as
adopted in section 2.1 can be expressed in the following
dimensionless forms:

**
**
*
0,
0, ;
xt
BxtB
x





 (46a)

**
**
*
1,
1, ;
xt
BxtB
x





 (46b)


**
,0xt  1
(46c)
The heat transfer from the pin to the flowing fluid is
given by



1
*
0
1
***
0
d
exp d
fd d
s
qhPLTTx
hPL TTCBxtx 




 



(47)
Define the dimensionless pin heat transfer rate C as
the ratio between the pin heat transfer rate to that having
maximum temperature difference of


s
TTT

 .
Mathematically, it is equal to

A. -R. A. KHALED
7

1
***
0
exp d
fd
C
qCBxt
hPL T


 

x

(48)
Closed Form Solutions
The solution of

**
,
x
t  can be decomposed into
sum of two solutions: 1) the steady state solution

*
sC
x

and, 2) the homogenous solution


**
,
C
x
t 
.
The corresponding governing equations for each one are
taken to be

222
*2 *
2
dd
22
dd
20
sC sC
f
f
f
PeBmLPe BB
xx
BBPe

sC




 



 
(49)

222
*2 *
*
22
CC
f
fC
C
f
PeBmLPe BB
xx
Pe t







 






(50)
The corresponding boundary and initial conditions are
taken to be

*
*
*
0
d0
d
sC sC
x
Bx B
x


; (51a)

*
*
*
1
d1
d
ssC
x
Bx B
x


; (51b)

**
**
*
0,
0, 0;
CC
xt
Bx t
x




(51c)

**
**
*
1,
1, 0;
CC
xt
Bx t
x





sC
(51d)

** *
,01
C
x
t   x  (51e)
According to Equation (48), C is always increasing
with time. The maximum value of C which is denoted
by max
C is of special importance to this work. It is
equal to C at the maximum available dimensionless
time (


*
fo
tx1L

). At that time,

**
,
x
t  is expected
to be equal to

*
sC
x
 . The solution of


*
sC
x
 as
obtained from solving Equation (49) is equal to
  
**
55 66
exp exp
sC * 2
x
CsxCsx   A
(52)
where A2, C5, C6, s5 and s6 are equal to

2
222
2;
2
f
f
BPe B
AmLBPe B

 (53a)

 
6
2
5
565
exp 1
1;
exp exp
s
A
CB
sB ss

 






(53b)

 
5
2
6
665
1exp
1;
exp exp
s
A
CB
sB ss

 






 





(53c)

2
2
5;
24
ff
f
Pe Pe
s
BPeBm



 L (53d)

2
2
624
ff
f
Pe Pe
s
BPeB



 mL (53e)
As such,


max
C
is equal to


 
 

5
5
max
5
6
6
6
2
exp exp
exp exp
exp 1
C
Bs
C
sB
Bs
C
sB
B
AB
 























(54)
Note that the maximum heat transfer rate can be ob-
tained and it is equal to

 

2exp
fdf fCs
m
qcAUTT 



1B


. Since m
can be obtained by solving the following equation:
0.99
fd fd
mm m
qq




. It is the solution of




2
max 1.98 exp1
Cf
mm
mLPe B



 (55)
2.4. Pins Moving Transversely Towards the
Heated Surface (Cases D)
Let the pin described in section 2.3 be aligned trans-
versely and be moving at a constant velocity U towards
the hot surface as shown in Figure 2. The heated surface
temperature is considered to be varying exponentially
with xs-axis that is coinciding with pin axial axis. This
variation is according to the following relationship:



 
2
exp
sso
Tx TTTbx



(56)
where b2 is a positive quantity. Accordingly, the fluid
stream temperature surrounding the pin given by Equa-
tion (41) is equal to



 
21
,exp
dso
TxxTT Tbxbx



' (57)
where Tso is the temperature of the surface opposing the
pin left end. In terms of dimensionless variables given by
Equation (3a) and Equation (23), Equation (57) changes to





*** *
22
,exp
dso
TxtTT TCBxt 
 
 
 
(58)
where B2, C and 
2 are equal to
22
;BbL

(59a)

8

A. -R. A. KHALED

1
exp ;
o
Cbx (59b)
11
;BbL (59c)

21f
BPeB  2

(59d)
According to Equation (57), the dimensionless time
required for the pin to reach the heated boundary is given
by

*
f
of
. Applying the dimensionless vari-
ables given by Equation (3a), Equation (44) and Equa-
tion (23) on Equation (25) will change it to the following
dimensionless form:
txLPe

222
221
*2 *
1*
2f
f
BmLBBPe
xx
BPet
 









2
2
B
(60)
The dimensionless boundaries and initial conditions as
adopted in section 2.1 can be expressed in the following
dimensionless forms:

 
**
**
**
22
*
0,
** **
22
*
1,
0, ;
1,;,0 1
xt
xt
Bxt B
x
BxtB xt
x






 

*
(61)
The heat transfer from the pin to the flowing fluid is
given by



1
*
0
1
**
22
0
d
exp d
fd d
so
qhPLTTx
hPL TTCBxtx 




 



(62)
Define the dimensionless pin heat transfer rate D as
the ratio between the pin heat transfer rate to that with
maximum temperature difference of

Dso
TTT

.
Mathematically, it is equal to

1
**
22
0
exp d
f
DD
qCBxt
hPL T


 

*
x
(63)
Closed Form Solutions
According to Equation (62), D is always increasing
with time. As such, the maximum value of D, denoted
by , is computed at dimensionless time given
by

max
D

*
fo
txL. At that time,


**
,
x
t  is expected to be
equal to

sD

*
x
 . The solution of

*
sD
x
 as obtained
from solving Equation (60) at large times is equal to
 
**
77 88
exp exp
sD * 3
x
CsxCsx   A (64)
where A3, C7, C8, s7 and s8 are equal to

2
12
322
12
;
f
f
BPe B
AmLBPeB

 (65a)

 
8
3
72
7287
exp 1
1;
exp exp
s
A
CB
sBs s
 
 





(65b)

 
7
3
82
828 7
1exp
1;
exp exp
s
A
CB
sBs s




 




(65c)

2
72 1
;
f
s
BmLBPe  (65d)

2
82 1
;
f
s
BmLBPe  (65e)
As such,


max
D
 is equal to




72 82
78
max
72 82
2
3
2
1exp 1exp
1exp
D
sB sB
CC
sB sB
BA
B

   

 
 

 


 







(66)
Equation (66) is reducible to the following expression:
 

12
2 max
2
1
exp 1
f
D
f
BPeB
B
mLBPe




 



(67)
The maximum effective swimming pin index denoted
by m can be obtained by solving the following equation:
0.99
fd fd
mmm
qq




. As such, the dimensionless
effective length for this case mL can be obtained to be
equal to 1 9.95
f
mL BPe
.
2.5. Effective Thermal Conductivity for the
Fluid Loaded With Swimming Pins of
Kind (A)
Suppose that the pin volume fraction is equal to
fsf
nV V


where nf is the number of swimming pins,
Vsf is the volume of a single pin and V is the fluid volume.
The maximum value of

is taken to be 1.5% which is
expected to cause insignificant effect on the fluid flow
pressure drop [5,19]. The net heat flux received by the
fluid can be shown to be equal to
o
fd
Co d
ds Co rr
q
AT
qq k
APL r



 
 
 
 
  (68)
where ACo, k and r are the pipe cross-sectional area


2
π
Co
A
r, fluid thermal conductivity and the pipe ra-
dial coordinate, respectively. For homogenous mixture of
the swimming pins and the pure fluid, the mixture can be
approximated as a continuum fluid with effective thermal
conductivity keffA. For this case, the boundary heat flux,
s
q

, is given by

A. -R. A. KHALED
9
o
d
s effA
rr
T
qk r

  (69)
By solving Eqs. (68) and (69) simultaneously, keffA can
be obtained and it is equal to

1
2
12
effAf oA
A
kk mL
r
kkLPe





  









(70)
where PeA is the pure fluid Peclet number;
2
Apmo
Pec urk

. Note that um is the pure fluid mean
velocity.
2.6. Effective Thermal Conductivity for the
Fluid Loaded With Swimming Pins of
Kind (B)
The steady state rate of heat transfer through the pin is
independent on the pin speed. As such, the effective
thermal conductivity can be obtained by equating the
transverse conduction across a given volume of fluid and
swimming pins (V = ACoL) to that across a homogenous
mixture with effective thermal conductivity keffB under
the same temperature difference. Mathematically, this
energy balance is given by

1dCo
CodeffB Co
C
TA
kAhPL TkA
LA



 


d
T
L
(71)
As such, keffB is given by:
 
1
11
cosh 2
effB f
kk
kk

mL





 







(72)
Based on effective pin length, Equation (72) is reduci-
ble to

10.99
effB f
kk
kk


 


(73)
2.7. Effective Thermal Conductivity for the
Fluid Loaded With Swimming Pins of
Kind (C)
The rate of heat transfer from the heated surface (per unit
cross-sectional area normal to x’-axis) is given by:


max
0
0
d1
1
d
d
d
d
d
C x
d
effC x
T
qk q
xA
T
kx





 


 
f d
(74)
As such, keffC can be obtained and it is equal to



2
max
1
effCf C
kk
mL
kBk



 

 (75)
2.8. Effective Thermal Conductivity for the
Fluid Loaded With Swimming Pins of
Kind (D)
The rate of heat transfer from the heated surface (per unit
cross-sectional area normal to x’-axis) is given by:

1
*
00
1
*
00
1
1d
d
d
f
d
C
x
d
effD
x
T
kx
xA
T
kx
x

q






 
 





 





(76)
Therefore, keffD can be obtained and it is equal to
 

2
2
1
1
effD f
f
f
kk
mL Pe
kk
mLBPe




 





(77)
Based on maximum effective pin index, Equation (76)
is reducible to

10.99
effD f
f
kk
Pe
kk


 
 (78)
3. Discussion of the Results
Figure 3 shows the variation of the dimensionless rate of
heat transferred from the fluid to the pin Awith the
pin thermal length mL, pin Peclet number Pef and di-
mensionless time t* for case A-swimming pins. Heat
transfer to the swimming pin is expected to increase as
mL increases however, the dominator of Equation (8)
increases largely with the increase of hPL. The latter
quaintly increases linearly with . As such, A


2
mL


is shown to decrease as mL increases. The initial value of
A

 is found from Figure 3 to be equal to 0.5. This
value coincides with the value obtained by integrating
Equation (11c) over the whole range of x* as given by
Equation (8). This validates the obtained closed form
solutions. As t* increases, A is found to increase at
lower values of mL while at large values of mL, A


 is
unaffected with the time variable. Increasing the value of
Pef causes an increase in A  . This is because pins
swimming at larger U-values (larger Pef-values) reach to
the fluid volumes with larger temperatures in a shorter
period of time. Thus, the temperature difference between
the fluid and the pin increases causing an increase in the
rate of the heat transfer to the pin.
Factors that increases the convection heat transfer to
the pin such as increasing the values of Pef and mL and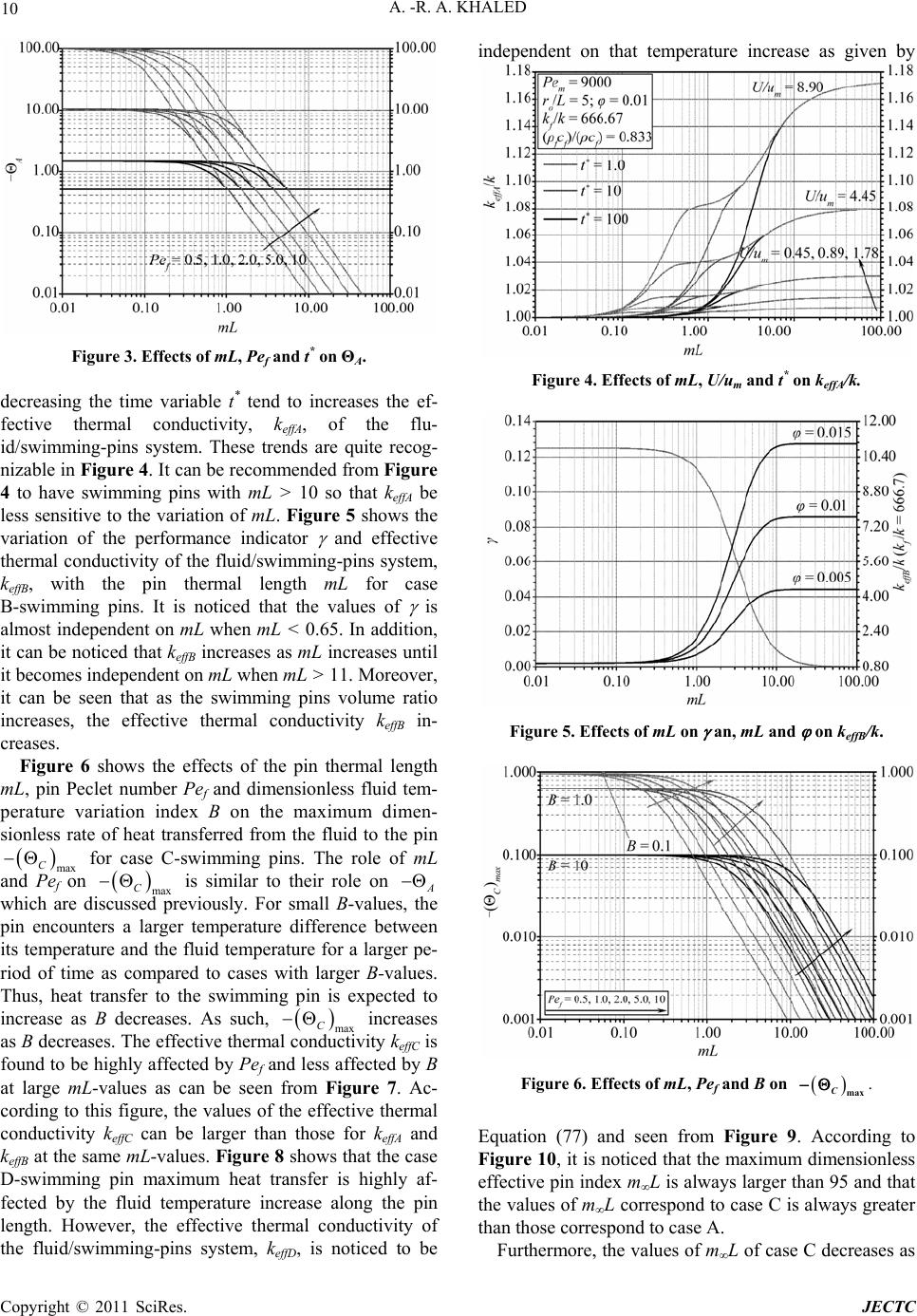

10 A. -R. A. KHALED
Figure 3. Effects of mL, Pef and t* on ΘA.
decreasing the time variable t* tend to increases the ef-
fective thermal conductivity, keffA, of the flu-
id/swimming-pins system. These trends are quite recog-
nizable in Figure 4. It can be recommended from Figure
4 to have swimming pins with mL > 10 so that keffA be
less sensitive to the variation of mL. Figure 5 shows the
variation of the performance indicator  and effective
thermal conductivity of the fluid/swimming-pins system,
keffB, with the pin thermal length mL for case
B-swimming pins. It is noticed that the values of  is
almost independent on mL when mL < 0.65. In addition,
it can be noticed that keffB increases as mL increases until
it becomes independent on mL when mL > 11. Moreover,
it can be seen that as the swimming pins volume ratio
increases, the effective thermal conductivity keffB in-
creases.
Figure 6 shows the effects of the pin thermal length
mL, pin Peclet number Pef and dimensionless fluid tem-
perature variation index B on the maximum dimen-
sionless rate of heat transferred from the fluid to the pin
for case C-swimming pins. The role of mL
and Pef on max
C is similar to their role on A

max
C





which are discussed previously. For small B-values, the
pin encounters a larger temperature difference between
its temperature and the fluid temperature for a larger pe-
riod of time as compared to cases with larger B-values.
Thus, heat transfer to the swimming pin is expected to
increase as B decreases. As such, max
C increases
as B decreases. The effective thermal conductivity keffC is
found to be highly affected by Pef and less affected by B
at large mL-values as can be seen from Figure 7. Ac-
cording to this figure, the values of the effective thermal
conductivity keffC can be larger than those for keffA and
keffB at the same mL-values. Figure 8 shows that the case
D-swimming pin maximum heat transfer is highly af-
fected by the fluid temperature increase along the pin
length. However, the effective thermal conductivity of
the fluid/swimming-pins system, keffD, is noticed to be
independent on that temperature increase as given by


Figure 4. Effects of mL, U/um and t* on keffA/k.
Figure 5. Effects of mL on  an, mL and  on keffB/k.
Figure 6. Effects of mL, Pef and B on .

max

C
Equation (77) and seen from Figure 9. According to
Figure 10, it is noticed that the maximum dimensionless
effective pin index mL is always larger than 95 and that
the values of mL correspond to case C is always greater
than those correspond to case A.
Furthermore, the values of mL of case C decreases as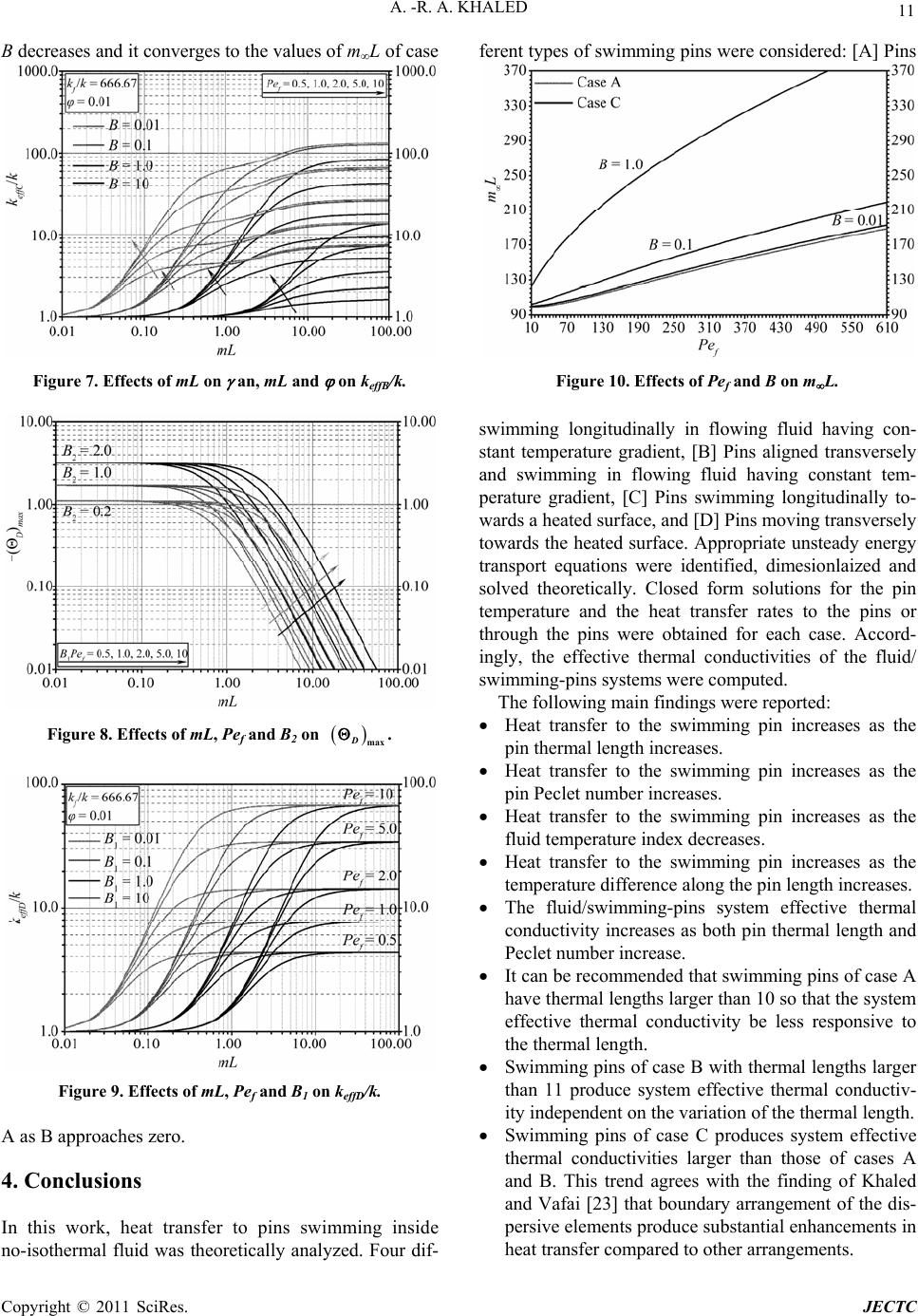

A. -R. A. KHALED
11
B decreases and it converges to the values of mL of case
Figure 7. Effects of mL on  an, mL and  on keffB/k.
Figure 8. Effects of mL, Pef and B2 on .

max
D
Figure 9. Effects of mL, Pef and B1 on keffD/k.
A as B approaches zero.
4. Conclusions
In this work, heat transfer to pins swimming inside
no-isothermal fluid was theoretically analyzed. Four dif-
ferent types of swimming pins were considered: [A] Pins
Figure 10. Effects of Pef and B on mL.
swimming longitudinally in flowing fluid having con-
stant temperature gradient, [B] Pins aligned transversely
and swimming in flowing fluid having constant tem-
perature gradient, [C] Pins swimming longitudinally to-
wards a heated surface, and [D] Pins moving transversely
towards the heated surface. Appropriate unsteady energy
transport equations were identified, dimesionlaized and
solved theoretically. Closed form solutions for the pin
temperature and the heat transfer rates to the pins or
through the pins were obtained for each case. Accord-
ingly, the effective thermal conductivities of the fluid/
swimming-pins systems were computed.
The following main findings were reported:
 Heat transfer to the swimming pin increases as the
pin thermal length increases.
 Heat transfer to the swimming pin increases as the
pin Peclet number increases.
 Heat transfer to the swimming pin increases as the
fluid temperature index decreases.
 Heat transfer to the swimming pin increases as the
temperature difference along the pin length increases.
 The fluid/swimming-pins system effective thermal
conductivity increases as both pin thermal length and
Peclet number increase.
 It can be recommended that swimming pins of case A
have thermal lengths larger than 10 so that the system
effective thermal conductivity be less responsive to
the thermal length.
 Swimming pins of case B with thermal lengths larger
than 11 produce system effective thermal conductiv-
ity independent on the variation of the thermal length.
 Swimming pins of case C produces system effective
thermal conductivities larger than those of cases A
and B. This trend agrees with the finding of Khaled
and Vafai [23] that boundary arrangement of the dis-
persive elements produce substantial enhancements in
heat transfer compared to other arrangements.

A. -R. A. KHALED
12
 Swimming pins of case D produces system effective
thermal conductivities independent on temperature
difference along the pin length.
Finally, the closed form solutions derived in this work
can form a basis for constructing and modeling super
convective fluidic systems that can be used in cooling of
electronic components.
5. Acknowledgments
The support of this work by King Abdulaziz City for
Science and Technology (KACST) under project no.
8-ENE192-3 is acknowledged.
6. References
[1] W. M. Kays, “Pin-Fin Heat-exchanger Surfaces,” Journal
of Heat Transfer-Transactions of the ASME, Vol. 77,
1955, pp. 471-483.
[2] D. O. Kern and A. D. Kraus, “Extended Surface Heat
Transfer”, McGraw-Hill, New York, 1972.
[3] A. D. Kraus, A. Aziz, and J. R. Welty, “Extended Surface
Heat Transfer,” John Wiley & Sons, Inc. New York,
2001.
[4] A. Nuntaphan, T. Kiatsiriroat and C. C. Wang, “Air Side
Performance at Low Reynolds Number of Cross-flow
Heat Exchanger using Crimped Spiral Fins,” Interna-
tional Communications in Heat and Mass Transfer, Vol.
32, No. 1-2, 2005, pp. 151-165.
doi:10.1016/j.icheatmasstransfer.2004.03.022
[5] X. -Q. Wang and A. S. Mujumdar, “Heat Transfer Char-
acteristics of Nanofluids: A Review,” International
Journal of Thermal Sciences, Vol. 46, No. 1, 2007, pp.
1-19. doi:10.1016/j.ijthermalsci.2006.06.010
[6] A. E. Bergles, “Handbook of Heat Transfer,”3rd Edition,
McGraw-Hill, New York, 1998, pp. 11.1-11.76.
[7] D. -K. Yang, K. -S. Lee and S. Song, “Fin Spacing Opti-
mization of a Fin-tube Heat Exchanger Under Frosting
Conditions,” International Journal of Heat and Mass
transfer, Vol. 49, No. 15-16, 2006, pp. 2619-2625.
doi:10.1016/j.ijheatmasstransfer.2006.01.016
[8] N. Sahiti, A. Lemouedda, D. Stojkovic, F. Durst and S.
Franz, “Performance Comparison of Pin Fin In-duct Flow
Arrays with Various Pin Cross-sections,” Applied Ther-
mal Engineering, Vol. 26, No. 11-12, 2006, pp. 1176-
1192. doi:10.1016/j.applthermaleng.2005.10.042
[9] M. Almogbel and A. Bejan, “Cylindrical Trees of Pin
Fin,” International Journal of Heat and Mass Transfer,
Vol. 43, No. 23, 2000, pp. 4285-4297.
doi:10.1016/S0017-9310(00)00049-1
[10] M. Almogbel, “Constructal Tree-Shaped Fins,” Interna-
tional Journal of Thermal Sciences, Vol. 44, No. 4, 2005,
pp. 342-348. doi:10.1016/j.ijthermalsci.2004.11.002
[11] L. Li, W. Cui, Q. Liao, X. Mingdao, T-C. Jen, Q. Chen,
“Heat Transfer Augmentation in 3D Internally Finned
and Microfinned Helical Tube,” International Journal of
Heat and Mass Transfer, Vol. 48, 2005, pp. 1916-1925.
doi:10.1016/j.ijheatmasstransfer.2004.12.003
[12] S. Kiwan and M. A. Al-Nimr, “Using Porous Fin for Heat
Transfer Enhancement,” Journal of Heat Trans-
fer-Transactions of the ASME, Vol. 123, No. 4, 2001, pp.
617-623. doi:10.1115/1.1371922
[13] T. K. Aldoss, M. A. Al-Nimr and M. Hader, “Using
Capsulated Liquid Metal Fins for Heat Transfer En-
hancement,” Journal of Enhanced Heat Transfer, Vol. 11,
No. 2, 2004, pp. 151-160.
doi:10.1615/JEnhHeatTransf.v11.i2.40
[14] A. -R. A. Khaled, “Maximizing Heat Transfer through
Joint Fin Systems,” Journal of Heat Transfe r-Transactions
of the ASME, Vol. 128, No. 2, 2006, pp. 203-206.
doi:10.1115/1.2137764
[15] A. -R. A. Khaled, “Investigation of Heat Transfer
Enhancement Using Permeable Fins,” Journal of Heat
Transfer-Transactions of ASME, Vol. 132, No. 3, 2010,
pp. 1-5. doi:10.1115/1.4000056
[16] A. -R. A. Khaled, “Heat Transfer Analysis through Solar
and Rooted Fins,” Journal of Heat Transfer-Transactions
of the ASME, Vol. 130, No. 8, 2008, Article no. 74503,
pp. 1-4.
[17] A. -R. A. Khaled, “Thermal Characterizations of
Fin-Thin Film Systems,” Journal of Heat Trans-
fer-Transactions of the ASME, Vol. 132, No. 10, 2010, pp.
1-6. doi:10.1115/1.4001647
[18] J. A. Eastman, S. U. S. Choi, S. Li, W. Yu and L. J.
Thompson, “Anomalously Increased Effective Thermal
Conductivities of Ethylene Glycol-based Nanofluids
Containing Copper Nanoparticles,” Applied Physics Let-
ters, Vol. 78, No. 6, 2001, pp. 718-720.
doi:10.1063/1.1341218
[19] Y. Xuan and Q. Li, “Investigation on Convective Heat
Transfer and Flow Features of Nanofluids,” Journal of
Heat Transfer – Transactions of the ASME, Vol. 125, No.
1, 2003, pp. 151-155. doi:10.1115/1.1532008
[20] M. Siddique, A. -R. A.Khaled, N. I. Abdulhafiz and A. Y.
Boukhary, “Recent Advances in Heat Transfer Enhance-
ments: A Review Report,” International Journal of
Chemical Engineering, Vol. 2010, Article ID 106461,
2010, pp.1-28. doi:10.1155/2010/106461
[21] F. P. Incorpera, D. P. DeWitt, T. L. Bergman, and A. S.
Lavine, “Fundamentals of Heat and Mass Transfer-6th
Edition,” John Wiley, New York, 2006.
[22] M. N. Ozisik, “Heat Conduction,” 2nd edition, John Wiley
& Sons, Inc., New York, 1993.
[23] A. -R. A. Khaled and K. Vafai, “Heat Transfer through
Control of Thermal Dispersion Effects,” International
Journal of Heat and Mass Transfer, Vol. 48, No. 11,
2005, pp. 2172-2185.
doi:10.1016/j.ijheatmasstransfer.2004.12.035

A. -R. A. KHALED
13
Nomenclature
A1-A3 steady state particular solutions; Equations
(17a), (53a) & (65a)
AC pin cross-sectional area
ACo pipe cross-sectional area
B, B1, B2 exponential functions dimensionless indices
b, b1, b2 exponential functions indices
C1-C8 steady state general solutions coefficients;
Equations (17b, c), (53b, c) & (65b, c)
cp pure fluid specific heat [J/kgK]
Ea, En homogenous solution coefficients; Equation
(19a, b)
Fn homogenous solution coefficients; Equation
(37)
g transformed dimensionless temperature; Equa-
tion (9) & Equation (31)
gs transformed dimensionless steady state tem-
perature; Equation (12) & Equation (35)
h convection heat transfer coefficient between
the pin and the fluid [W/m2K]
k pure fluid thermal conductivity [W/m.K]
keff Effective fluid-swimming pins thermal con-
ductivity; Equation (70), (72), (75) & (77)
kf pin thermal conductivity [W/m.K]
L pin length [m]
m pin index [m]
n Integer (n = 1, 2, 3, , )

nf number of swimming pins
PeA Peclet number for case A (PeA =  cpum2ro/k)
Pef pin Peclet number (Pef = 
fcfUL/kf)
qf-d total convection heat transfer rate from the pin
to the fluid [W]
qf pin maximum conduction heat transfer rate
[W]
r radius axis [m]
ro inner radius of the pipe [m]
s1-s8 steady state general solutions exponential di-
mensionless indices; Equations 17(d, e), 53(d,
e) & 65(d, e)
Td pin surrounding fluid temperature [K]
Td,i pin surrounding fluid temperature at the pipe
inlet [K]
Tf pin temperature [K]
Ts heated surface temperature [K]
Tso reference heated surface temperature [K]
T outer fluid free stream temperature [K]
t time variable [s]
t* Dimensionless time; Equation (3b) & Equa-
tion (23)
U swimming pin velocity [m/s]
um Mean fluid velocity inside the pipe for cases
(A) and (B) [m/s]
V Fluid and swimming pins volume per pin
length (V = ACoL)
Vsf Volume of single pin (Vsf = ACL)
x pin axial coordinate [m]
x' pin leading edge position vector [m]
xo pin leading edge initial position vector [m]
x* dimensionless x-coordinate (x*=x/L)
Greek symbols
 dimensionless pin convection heat transfer;
Equations (8), (30), (48) & (63)
12
,

 characteristic functions; Equation (5c) & Equ-
ation (27a)
 pin maximum dimensionless conduction heat
transfer for case B; Equation (40)
 Swimming pins to fluid volume ratio


fsf
nV V  

1,

2 pin to fluid temperature difference ratios times
pin Peclet number; Equations (27b) (59d)
 pin dimensionless temperature; Equation (3c)
& Equation (44)
 inner fluid density [kg/m3]
 homogenous solution; Equation (16) & Equa-
tion (36)
Subscripts
A, B, C, D cases A, B, C and D
s steady state