Materials Sciences and Applicatio ns, 2011, 2, 669-675
doi:10.4236/msa.2011.26092 Published Online June 2011 (http://www.SciRP.org/journal/msa)
669
Modeling and Optimization of Electrical
Discharge Machining of SiC Parameters, Using
Neural Network and Non-dominating Sorting
Genetic Algorithm (NSGA II)
Ramezan Ali MahdaviNejad
School of mechanical Engineering, College of Engineering, University of Tehran, Tehran, Iran.
Received December 29th, 2010; revised March 28th, 2011; accepted May 18th, 2011.
ABSTRACT
Silicon Carbide (SiC) machining by traditional methods with regards to its high hardness is not possible. Electro Dis-
charge Machining, among non-tradition al machining methods, is used for machining of SiC. The pr esent work is aimed
to optimize the surface roughness and material removal rate of electro discharge machining of SiC parameters simul-
taneously. As the output parameters are conflicting in nature, so there is no single combination of machining parame-
ters, which provides the best ma ch ining p erforman ce. Artificia l n eural network (ANN) with ba c k pr opa gatio n a lgo rithm
is used to model the process. A multi-objective optimization method, non-dominating sorting genetic algorithm-II is
used to optimize the process. Affects of three important input parameters of process viz., discharge current, pulse on
time (Ton), pulse off time (Toff) on electric discharge machining o f SiC are considered . Exp erim ents have b een condu cted
over a wide range of considered input parameters for training and verification of the model. Testing results demon-
strate that the model is suitable fo r predicting the response parameters. A pareto-optima l set has been predicted in this
work.
Keywords: Electro Discharge Machining, Non- Dominating Sorting Algorithm, Neural Network, REFEL SiC
1. Introduction
Electrical discharge machining (EDM) is one of the most
extensively used non-conventional material removal
process. Its unique feature of using thermal energy to
machine electrically conductive parts regardless of hard-
ness has been its distinctive advantage in the manufac-
ture of mould, die, automotive, aerospace and surgical
component [1]. The selection of appropriate parameters
for maximum material removal rate and minimum sur-
face roughness during the EDM process traditionally
carried out by the operator’s experience or conservative
technological data provided by the EDM equipment
manufacturers, which produced inconsistent machining
performance.[2]
Some researchers carried out various investigations to
improve the stock material removal rate and surface fin-
ishing in EDM process. Proper selection of machining
parameters for the best process performance is still a
challenging job.
Wang et al. [3] used genetic algorithm (GA) with arti-
ficial neural network (ANN) to find out optimal main
output parameters such as material removal rate and sur-
face roughness. They used ANN to model the process
and Hunter Software to solve multi-objective optimiza-
tion problem. Using ANN and GA, Su et al. [4] opti-
mized EDM parameters, roughing and finishing machin-
ing stages. They utilized artificial neural network to es-
tablish the relationship between the process parameters
and outputs. GA with properly defined objective func-
tions was then adapted to the neural network to deter-
mine the optimal process parameters. They transformed
material removal rate, tool wear and surface roughness
into a single objective. Rao et al. [7] used ANN and GA
to optimize the surface roughness of die sinking electric
discharge machining (EDM) by considering the simulta-
neous affect of various input parameters. Genetic algo-
rithm concept was used to optimize the weighting factors

Modeling and Optimization of Electrical Discharge Machining of SiC Parameters, Using Neural Network and 670
Non-dominating Sorting Genetic Algorithm (NSGA II)
of the network.
Pal et al. [1] used non dominating sorting genetic al-
gorithm-II to optimize the process. They conducted some
experiments on C40 Steel to generate input and output
data for training an ANN model. Material removal rate
and tool wear were two objectives to be optimized. So
they predicted a pareto-optimal set for outputs.
In this study material removal rate and surface rough-
ness have been considered to produce a pareto-optimal
set for EDM of REFEL SiC. Some related properties of
this material are shown in Table 1.
2. Experimentations
In this study, Deckel CNC Spark, ISO frequency system,
with gap control system was used to carry out the ex-
periments. Copper electrode was selected to drill holes in
the REFEL SiC blocks. For evaluating the EDM process
the MRR and surface roughness (Ra) are mentioned with
input machining parameters such as pulse on time (Ton),
pulse off time (Toff), discharge current (I). Proper selec-
tion of the machining parameters can result a higher ma-
terial removal rate and lower Ra. Using an orthogonal
array L25 according Taguchi method decreased the num-
ber experiments effectively. Hence 25 sets of experi-
ments have been conducted with five levels of each pa-
rameter (current, pulse on time and off time) to collect
for training of the neural network model. Moreover five
sets of experiments have been for testing the trained
neural network. For each experiment, a new set of tool
and work-piece has been used. For normal polarity the
work-piece is connected to the negative terminal and the
tool is connected to the positive terminal of the source,
where as for reverse polarity it is just the opposite. Ex-
periment has been performed with normal polarity. The
current range is 0.1 - 5 A and the pulse on time and pulse
off time ranges are 21 - 1125 µs.
3. Material Removal Rate (MRR)
Material removal rate and surface roughness have been
used to evaluate machining performance. Material re-
moval rate (MRR) is calculated from the difference of
weight of work piece before and after experiment.

SiC
MRR if
ww
t 

 mm3/min (1)
where, wi is the initial weight of workpiece in g; wf the
weight of workpiece after machining in g; t the machin-
ing time in minutes; SiC

is the density of SiC (3.1×
10–3 g/mm3).
4. Surface Roughness
The surface roughness Ra is the arithmetic average of
collected roughness data points and given by the sum of
the absolute values of all the areas above and below the
mean line (in integrally form). A mean line is found that
is parallel to the general surface direction and divides the
surface in such a way that the sum of the areas formed
above the line is equal to the sum of the areas formed
below the line. When sample points were taken, R
a is
calculated as follows:
1
1n
a
i
R
n
i y (2)
where yi is the distance between the ith sample point on the
profile from the mean line, and n is the number of sample
points.
5. Neural Network
Modeling of EDM with feed forward neural network is
composed of two stages: training and testing of the net-
work with experimental machining data. The scale of the
input and output data is an important matter to consider,
especially, when the operating ranges of process pa-
rameters are different. The scaling or normalization en-
sures that the ANN will be trained effectively. By
searching in different network architectures using a
MATLAB code, multilayer-perceptron (3-5-5-2) was
chosen as the network architecture. The networks were
trained using a back-propagation algorithm. The selected
network architecture had the minimum value of the error.
The error E indicates the difference between the actual
and the desired output of the neural network, as follows:


2
1min
az
jj
j
Eya


 (3)
where yj is the desired output, aj is the calculated output,
az the number of testing data. Five sets of experiments
allocated to test the network’s error value. Pulse on-time,
pulse off-time and the current are the inputs of neural
network and material removal rate and surface roughness
are the outputs of the neural network. Figure 1 shows the
Table1. Some characteristics of REFEL SiC [5].
Density
(gr/cm3)
Hardness
(HV)
Young modulus
(E) (GN/m)
Thermal
expansion
1 × 10–6˚C
Thermal conductivity
(k) at 100˚C (W/m·˚C)
at 1200˚C
Specific heat
(J/g˚C)
Electrical resistance
(Ω·cm)
Thermal shock
(cal/cm·s) at 500˚C
3.10 2500 413 4.3 83.6 38.9 670.710 0.42 (at 25˚C)
0.016 (at 1200˚C) 59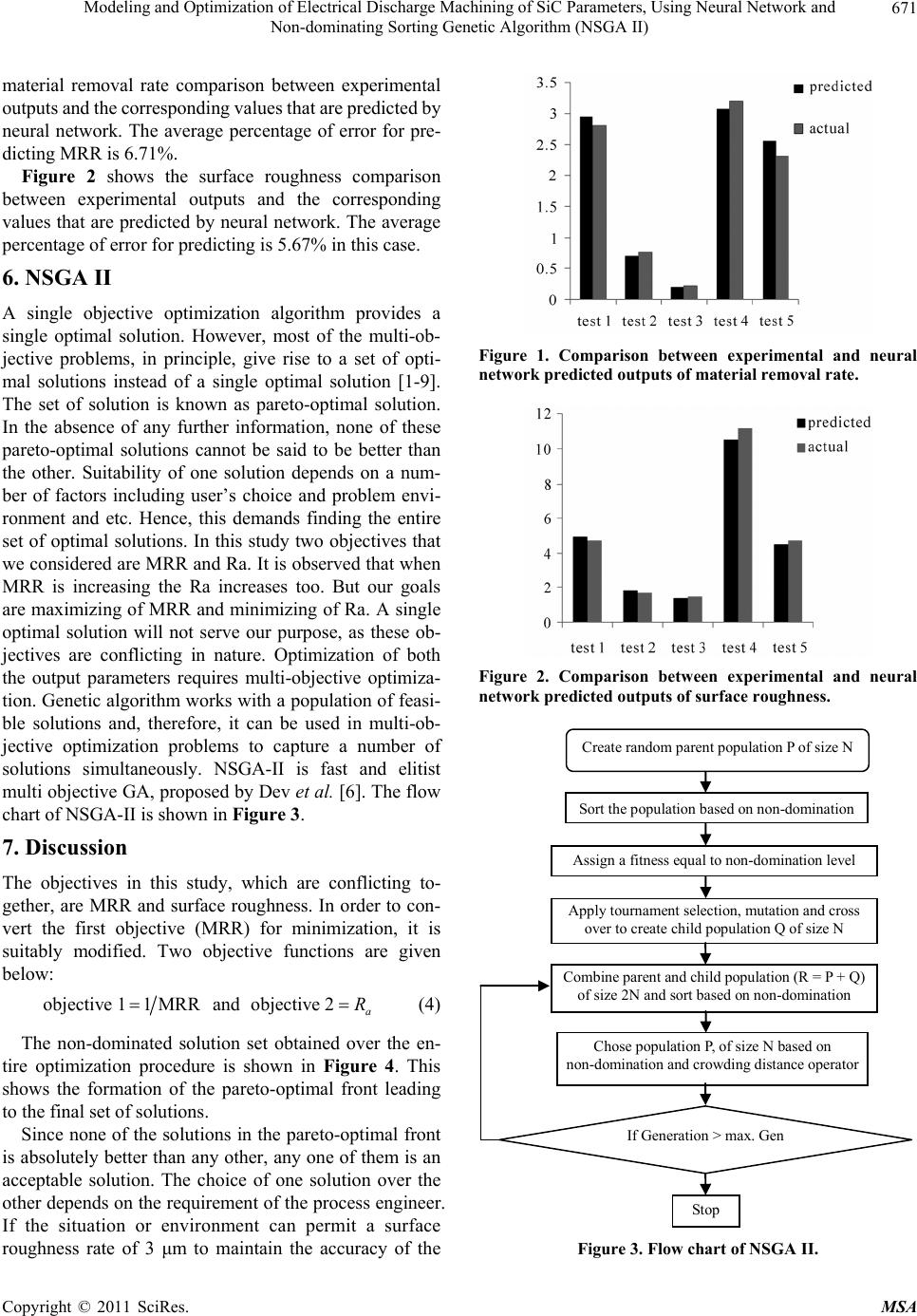

Modeling and Optimization of Electrical Discharge Machining of SiC Parameters, Using Neural Network and 671
Non-dominating Sorting Genetic Algorithm (NSGA II)
material removal rate comparison between experimental
outputs and the corresponding values that are predicted by
neural network. The average percentage of error for pre-
dicting MRR is 6.71%.
Figure 2 shows the surface roughness comparison
between experimental outputs and the corresponding
values that are predicted by neural network. The average
percentage of error for predicting is 5.67% in this case.
6. NSGA II
A single objective optimization algorithm provides a
single optimal solution. However, most of the multi-ob-
jective problems, in principle, give rise to a set of opti-
mal solutions instead of a single optimal solution [1-9].
The set of solution is known as pareto-optimal solution.
In the absence of any further information, none of these
pareto-optimal solutions cannot be said to be better than
the other. Suitability of one solution depends on a num-
ber of factors including user’s choice and problem envi-
ronment and etc. Hence, this demands finding the entire
set of optimal solutions. In this study two objectives that
we considered are MRR and Ra. It is observed that when
MRR is increasing the Ra increases too. But our goals
are maximizing of MRR and minimizing of Ra. A single
optimal solution will not serve our purpose, as these ob-
jectives are conflicting in nature. Optimization of both
the output parameters requires multi-objective optimiza-
tion. Genetic algorithm works with a population of feasi-
ble solutions and, therefore, it can be used in multi-ob-
jective optimization problems to capture a number of
solutions simultaneously. NSGA-II is fast and elitist
multi objective GA, proposed by Dev et al. [6]. The flow
chart of NSGA-II is shown in Figure 3.
7. Discussion
The objectives in this study, which are conflicting to-
gether, are MRR and surface roughness. In order to con-
vert the first objective (MRR) for minimization, it is
suitably modified. Two objective functions are given
below:
objective 11MRR and o (4) bjective 2a R
The non-dominated solution set obtained over the en-
tire optimization procedure is shown in Figure 4. This
shows the formation of the pareto-optimal front leading
to the final set of solutions.
Since none of the solutions in the pareto-optimal front
is absolutely better than any other, any one of them is an
acceptable solution. The choice of one solution over the
other depends on the requirement of the process engineer.
If the situation or environment can permit a surface
roughness rate of 3 μm to maintain the accuracy of the
Figure 1. Comparison between experimental and neural
network predicted outputs of material removal rate.
Figure 2. Comparison between experimental and neural
network predicted outputs of surface roughness.
Apply tournament selection, mutation and cross
over to create child population Q of size N
Create random parent population P of size N
Assign a fitness equal to non-domination level
Sort the population based on non-domination
Combine parent and child population (R = P + Q)
of size 2N and sort based on non-domination
Chose population P, of size N based on
non-domination and crowding distance operator
If Generation > max. Gen
Stop
Figure 3. Flow chart of NSGA II.

Modeling and Optimization of Electrical Discharge Machining of SiC Parameters, Using Neural Network and 672
Non-dominating Sorting Genetic Algorithm (NSGA II)
Table 2. Optimal sets of parameters.
Ti To I MRR Ra
1 858.9584 924.4639 4.8902 3.6446 8.4364
2 141.5017 496.6855 0.1 0.3466 0.886
3 174.6221 682.9052 1.0473 1.4528 1.1667
4 316.126 21 3.8979 1.9901 1.1703
5 206.7583 663.0539 4.1795 3.5945 5.5242
6 168.7212 536.2421 4.2317 3.5695 5.0381
7 429.4838 70.5361 4.5337 2.3535 1.4294
8 407.6555 101.8867 4.5579 2.4078 1.5658
9 431.1151 33.2454 4.5007 2.2597 1.2826
10 372.2205 1082.09 3.9459 2.5234 1.6222
11 299.4541 937.1161 3.2485 3.2904 3.5347
12 349.6336 21 4.2386 2.1084 1.1764
13 133.5872 406.38 3.9202 3.4407 4.251
14 180.275 545.7843 0.5586 0.676 0.9604
15 120.2597 409.5408 3.9015 3.4017 4.0785
16 942.8562 855.8315 4.5168 3.6315 6.7868
17 287.1614 1024.018 3.0806 2.8177 1.7393
18 284.3813 1032.874 3.0924 2.7484 1.7079
19 877.9769 938.2853 4.871 3.6442 7.9565
20 171.6979 605.3086 0.7507 0.9007 1.0196
21 194.7966 529.194 0.7099 0.8277 1.0017
22 403.2268 21.0838 4.4904 2.1987 1.2137
23 300.4237 948.3546 3.2485 3.2873 3.117
24 113.1908
369.4054 3.8439 3.2937 3.8086
25 917.4061 941.7156 4.8294 3.6407 7.5638
26 916.4971 891.0667 4.6921 3.6398 7.379
27 984.2048 816.5333 4.4308 3.6187 6.2749
28 303.9082 938.2599 3.2566 3.2897 3.3114
29 1046.005 805.3527 4.3747 3.5948 5.7939
30 870.1822 924.2211 4.8671 3.6445 8.21
31 281.8689 1032.299 3.0245 2.6488 1.6937
32 315.6009 21 3.9119 1.993 1.1704
33 181.5296 531.0391 0.6132 0.7553 0.9725
34 275.9709 1016.142 3.0625 2.9787 1.809
35 131.772 491.3254 4.1534 3.5081 4.5261
36 305.2944 948.2171 3.2467 3.2833 2.8871
37 861.9278 930.9182 4.8708 3.6445 8.1551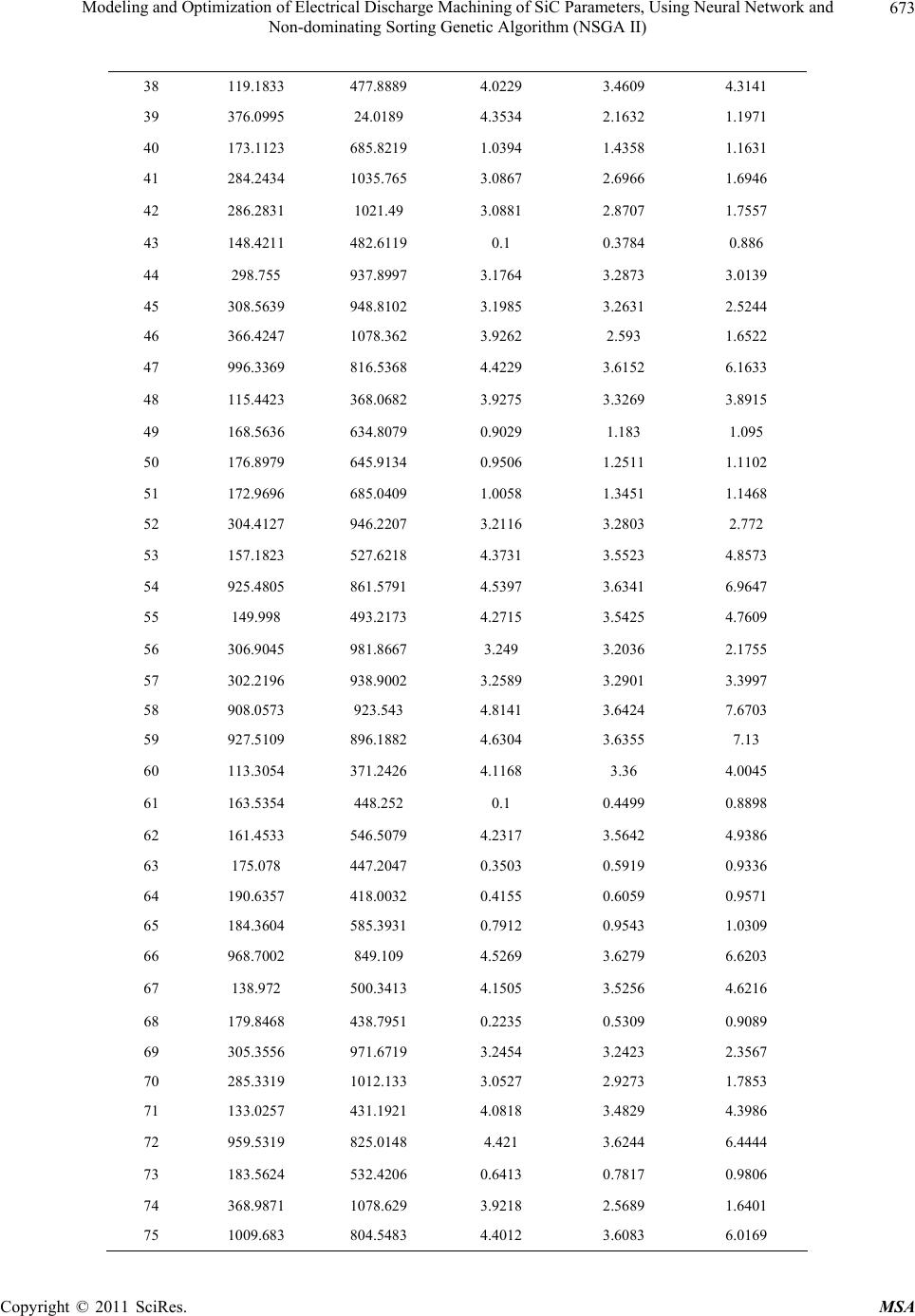

Modeling and Optimization of Electrical Discharge Machining of SiC Parameters, Using Neural Network and 673
Non-dominating Sorting Genetic Algorithm (NSGA II)
38 119.1833 477.8889 4.0229 3.4609 4.3141
39 376.0995 24.0189 4.3534 2.1632 1.1971
40 173.1123 685.8219 1.0394 1.4358 1.1631
41 284.2434 1035.765 3.0867 2.6966 1.6946
42 286.2831 1021.49 3.0881 2.8707 1.7557
43 148.4211 482.6119 0.1 0.3784 0.886
44 298.755 937.8997 3.1764 3.2873 3.0139
45 308.5639 948.8102 3.1985 3.2631 2.5244
46 366.4247 1078.362 3.9262 2.593 1.6522
47 996.3369 816.5368 4.4229 3.6152 6.1633
48 115.4423 368.0682 3.9275 3.3269 3.8915
49 168.5636 634.8079 0.9029 1.183 1.095
50 176.8979 645.9134 0.9506 1.2511 1.1102
51 172.9696 685.0409 1.0058 1.3451 1.1468
52 304.4127 946.2207 3.2116 3.2803 2.772
53 157.1823 527.6218 4.3731 3.5523 4.8573
54 925.4805 861.5791 4.5397 3.6341 6.9647
55 149.998 493.2173 4.2715 3.5425 4.7609
56 306.9045 981.8667 3.249 3.2036 2.1755
57 302.2196 938.9002 3.2589 3.2901 3.3997
58 908.0573 923.543 4.8141 3.6424 7.6703
59 927.5109 896.1882 4.6304 3.6355 7.13
60 113.3054 371.2426 4.1168 3.36 4.0045
61 163.5354 448.252 0.1 0.4499 0.8898
62 161.4533 546.5079 4.2317 3.5642 4.9386
63 175.078 447.2047 0.3503 0.5919 0.9336
64 190.6357 418.0032 0.4155 0.6059 0.9571
65 184.3604 585.3931 0.7912 0.9543 1.0309
66 968.7002 849.109 4.5269 3.6279 6.6203
67 138.972 500.3413 4.1505 3.5256 4.6216
68 179.8468 438.7951 0.2235 0.5309 0.9089
69 305.3556 971.6719 3.2454 3.2423 2.3567
70 285.3319 1012.133 3.0527 2.9273 1.7853
71 133.0257 431.1921 4.0818 3.4829 4.3986
72 959.5319 825.0148 4.421 3.6244 6.4444
73 183.5624 532.4206 0.6413 0.7817 0.9806
74 368.9871 1078.629 3.9218 2.5689 1.6401
75 1009.683 804.5483 4.4012 3.6083 6.0169

Modeling and Optimization of Electrical Discharge Machining of SiC Parameters, Using Neural Network and
Non-dominating Sorting Genetic Algorithm (NSGA II)
674
76 176.643 618.4106 0.9651 1.2652 1.1409
77 134.2186 431.9405 4.1533 3.4907 4.4421
78 961.3217 825.2114 4.4227 3.6242 6.4331
79 172.7149 683.4143 0.9945 1.3194 1.1413
80 301.2341 945.2716 3.1541 3.2729 2.6102
81 300.4964 945.9148 3.165 3.2768 2.6725
82 143.7192 487.6615 4.2564 3.5319 4.6777
83 174.965 613.1224 0.8278 1.03 1.05
84 159.3381 649.6514 0.8593 1.0943 1.0768
85 966.0411 847.5901 4.5269 3.6284 6.6415
86 305.7388 981.1644 3.2702 3.2229 2.2694
87 925.6356 861.3723 4.556 3.6351 7.005
88 276.5219 994.4977 2.9962 3.0797 1.8856
89 886.8913 930.2199 4.8374 3.6436 7.8378
90 182.7754 581.0766 0.8067 0.9855 1.0385
91 988.0573 799.9433 4.3565 3.6126 6.0526
92 293.829 1021.771 3.1564 2.9067 1.7773
93 178.411 630.8943 0.905 1.1575 1.0854
94 298.351 964.5621 3.0682 3.1826 2.0974
95 1001.796 801.5891 4.3056 3.605 5.8814
96 158.8948 650.0343 0.8593 1.0945 1.0774
97 278.2378 991.8914 2.9667 3.0496 1.8586
98 283.6434 966.2962 3.093 3.253 2.4188
99 935.8522
898.663 4.6975 3.6379 7.2202
100 115.3983 370.507 3.8796 3.3179 3.8653
product, the process engineer can chose the parameter
setting according to that to obtain maximum material
removal rate at the specified value of surface roughness.
From the experiments results, material removal and
surface roughness are 3.58 mm3/min and 7.34 μm respec-
tively. In this case the pulse on and pulse off times and
also the current settings are 850 µs, 900 µs and 5A re-
spectively. For solution number 1 in Figure 1, material
removal rate and Surface roughness are 3.6446 mm3/min
and 7.2561 μm, where the pulse on and pulse off times
and also current settings are 858.9584, 924.463 µs and
4.8902A, respectively. Choice of pulse on time and off
time will help to achieve higher MRR with same tool
wear. This indicates, values obtained from the optimiza-
tion technique are in close agreement with the experi-
mental values for more or less the same parameter set-
tings.
Figure 4. Pareto-optimal set.

Modeling and Optimization of Electrical Discharge Machining of SiC Parameters, Using Neural Network and 675
Non-dominating Sorting Genetic Algorithm (NSGA II)
8. Conclusions
81 experiments have been conducted with a wide range
of current, pulse on time and pulse off time. The MRR
and surface roughness have been measured for each set-
ting of pulse on time and pulse off time and current. An
ANN model has been trained within the experimental
data. Various ANN architectures have been studied, and
3-5-5-2 is selected. Material removal rate and surface
roughness have been optimized as objectives by using a
multi-objective optimization method. Non-dominating
sorting genetic algorithm-II and finally pareto-optimal
sets of material removal rate and surface roughness are
obtained. The results are shown in Table 2.
REFERENCES
[1] S. K. Pal, D. Mandal and P. Saha, “Modeling of Electrical
Discharge Machining Process Using Back Propagation
Neural Network and Multi-Objective Optimization Using
Non-Dominating Sorting Genetic Algorithm-II,” Journal
of Materials Processing Technology, Vol. 186, No. 1-3,
2007, pp. 154-162. doi:10.1016/j.jmatprotec.2006.12.030
[2] G. K. M. Rao, G. Rangajanardhaa, D. H. Rao and M. S.
Rao, “Development of Hybrid Model and Optimization of
Surface Roughness in Electric Discharge Machining Us-
ing Artificial Neural Networks and Genetic Algorithm,”
Journal of Materials Processing Technology, Vol. 209,
No. 3, 2009, pp. 1512-1520.
doi:10.1016/j.jmatprotec.2008.04.003
[3] K. Wang, H. L. Gelgele, Y. Wang, Q. Yuan and M. Fang,
“A Hybrid Intelligent Method for Modeling the EDM
Process,” International Journal of Machine Tools and
Manufacture, Vol. 43, No. 10, 2003, pp. 995-999.
doi:10.1016/S0890-6955(03)00102-0
[4] J. C. Su, J. Y. Kao and Y. S. Tarng, “Optimization of the
Electrical Discharge Machining Process Using a GA-
Based Neural Network,” International Journal of Ad-
vanced Manufacturing Technology, Vol. 24, 2004, pp.
81-90.
[5] R. Mahdavinejad, M. Tolouei-Rad and H. Sharifi Bidgoli,
“Heat Transfer Analysis of EDM Process on Silicon Car-
bide,” International Journal of Numerical Methods for
Heat and Fluid Flow, Vol. 15, No. 5, 2005, pp. 483-502.
doi:10.1108/09615530510593657
[6] K. Dev, A. Pratap, S. Agarwal and T. Meyarivan, “A Fast
and Elitist Multi Objective Genetic Algorithm: NSGA-II,”
IEEE Transactions on Evolutionary Computation, Vol. 6,
No. 2, 2002, pp. 182-197.
[7] G. K. M. Rao, G. Rangajanardhaa, D. H. Rao and M. S.
Rao, “Development of Hybrid Model and Optimization of
Surface Roughness in Electric Discharge Machining Us-
ing Artificial Neural Networks and Genetic Algorithm,”
Journal of Materials Processing Technology, Vol. 209,
No. 3, 2009, pp. 1512-1520.
doi:10.1016/j.jmatprotec.2008.04.003