Materials Sciences and Applications, 2011, 2, 526-536
doi:10.4236/msa.2011.26071 Published Online June 2011 (http://www.SciRP.org/journal/msa)
Geometrical Modeling of Crystal Structures with
Use of Space of Elliptic Riemannian Geometry
Stanislav Rudnev1, Boris Semukhin2, Andrey Klishin1
1Tomsk Polytechnic University, Tomsk, Russia; 2Institute of Strength Physics and Materials Science SB RAS, Tomsk, Russia.
Received February 28th, 2011; revised March 21st, 2011; accepted April 6th, 2011.
ABSTRACT
The space of internal geometry of a model of a real crystal is supposed to be finite, closed, and with a constant Gaus-
sian curvature equal to unity, permitting the realization of lattice systems in accordance with Fedorov groups of trans-
formations. For visualizing computations, the interpretation of geometrical objects on a Clifford surface (SK) in Rie-
mannian geometry with the help of a 2D torus in a Euclidean space is used. The F-algorithm ensures a computation of
2D sections of models of point systems arranged perpendicularly to the symmetry axes l3, l4, and l6. The results of mod-
eling can be used for calculations of geometrical sizes of crystal structures, nanostructures, parameters of the cluster
organization of oxides, as well as for the development of practical applications connected with improving the structural
characteristics of crystalline materials.
Keywords: F-Algorithm, Crystal Lattice Systems, Microstructure, Riemannian Geometry, Space of Interpretation
1. Introduction
Modern material science, building on very different
models of the structure of a substance, tries to create ab-
solutely new materials or materials with properties
needed when exploiting machines and mechanisms under
unusual conditions. Let us note that some successes are
recently observed in making materials with a structure
modeled at very different scaled and dimensional levels
it is the so-called nanomaterials technology. However,
essential breakthroughs in applications of these materials
when fabricating microelectronic engineering have not
yet been made. In our opinion, an essential value has the
fact that all up-to-date models are based only on one no-
tion of the structure of a solid, namely, considered in a
Euclidean space.
In the present paper we offer the other, alternative ap-
proach to describing both a structure and making materi-
als with special or unique properties by means of inter-
preting the space of experience and processing materials
in a strictly symmetrized electromagnetic field.
Development of physicochemical methods of investi-
gating a crystal structure and processing technologies,
growing needs for production of high quality crystalline
materials arouse a lot of attention to new approaches
grounded on modeling crystal structures with the use of
different modeling spaces. At the present time, concepts
of non-Euclidean phase spaces are ever more widely
used for describing general evolutionary principles of
various physical systems. In this connection, a particular
interest of researchers to problems of a possible realiza-
tion of Fedorov groups in non-Euclidean spaces is noted.
The realization of Fedorov groups of symmetry was con-
sidered in a pseudo-Euclidean space, Lobachevsky space
and Minkowski space [1]. A lack of similar examinations
is that in the specified spaces a space of infinite extent is
used for a model of lattices [2,3].
It is traditionally accepted to construct the crystal
structure of an ideal crystal by the multiplication of a
finite number of atoms by all transformations from some
Fedorov group in a Euclidean space. But such a con-
struction of an ideal crystal is not related to natural
causes of the growth of a real crystal, its finite (localised)
character and shape restricted in the space. Besides, the
problem of the relation of the internal structure and ex-
ternal faceting of a real crystal remains unresolved. An
ambiguity of the geometrical interpretation of the space
of the real crystal of minerals has led to the necessity of
developing models by using a non-Euclidean method of
describing crystal structures.
When modeling under the conditions of Riemannian
geometry, it will be natural to maintain the term “Fe-
dorov group” for discrete groups of movements, which

Geometrical Modeling of Crystal Structures with Use of Space of Elliptic Riemannian Geometry527
we shall denote by F-groups. For a model of the crystal
structure in an elliptic space, as well as in the Euclidean
case, the conditions of the global discreteness and ho-
mogeneity are fulfilled. In the case of F-groups the fi-
niteness theorem for the volume of the fundamental do-
main of a finite polyhedron is rather simply proved.
When modeling crystal structures, the space of Rie-
mannian geometry (V4) with the constant Gaussian cur-
vature К = 1, that coincides in sufficiently small regions
with a Euclidean space (a locally Euclidean space), was
chosen as a modeling space. When constructing crystal
lattices, simulated groups of transformations, which are
used for computations of point systems, are the basic tool
of investigating. In this case we deal with a finite space
where the distance between any two points does not ex-
ceed a certain value [4-8].
2. Geometrical Approach to Modeling
Crystal Structures
2.1. Space of Interpretation RE
Historically developed priority of Euclidean geometry
(despite the discoveries of non-Euclidean geometries)
has led to two fundamental consequences:
1) Up till now, the space of our experience is supposed
to be Euclidean,
2) All the laws of physics and chemistry are supposed
to be realizing in a Euclidean space.
And though mathematicians and, partly, physicists do
not forget to repeat that with N. Lobachevsky, J. Bolyai
and B. Riemann’s discoveries Euclidean geometry has
lost its unique position as the singular geometry of the
space of our experience, the problem of the choice of an
adequate geometrical space is still open. Nevertheless, a
reliable experimental confirmation of the fulfillment of
Coulomb’s law in non-Euclidean spaces has not yet been
obtained, and so far it is not clear how it can be realized.
However, after A. Poincaré constructed the interpreta-
tion (a model) of a non-Euclidean geometry (realizing
Lobachevsky’s plane), the situation changed radically. It
turned out that Euclidean geometry itself and, accord-
ingly, a Euclidean space are no more than one of a vari-
ety of geometrical interpretations. There arises the
unique possibility of considering the interpretation (rep-
resentation) of one geometry by means of geometrical
images of other geometry, of course, according to strictly
defined rules.
A considerable quantity of modern investigations
which can be found in [1] is devoted to interpretation
problems. For constructing geometrical models of crystal
structures the approach applied in [9] has been used.
A general scheme for the interpretation of elliptic Rie-
mannian geometry in a Euclidean space (
R
E
I
) is simple
enough.
A certain geometrical image A of the Riemannian
space 4
A
V

, possessing necessary properties, is chosen
as an object of the interpretation in a Euclidean space,
with the help of some geometrical image B of the
Euclidean space,


,
R
E
I
AB

where The
chosen geometrical image B of the Euclidean space is
endowed with properties of the geometrical image A, and
becomes, thus, а carrier of properties of the geometrical
image of the Riemannian space in the Euclidean space.
3.BR
Operations with the geometrical image B are executed
according to the rules of the Riemannian space with re-
gard to certain conditions stated below. Consequently, in
the Euclidean space there arises a certain region RE
which is called the space of interpretation.


R
E
E
I
MR, (1)
where M is the Riemannian space being subject to the
interpretation.
Properties of the space RE are sufficiently specific and
taken into consideration in each specific case.
A Clifford surface SK—a direct circular cylinder of the
elliptic space [10] is chosen as the basic geometrical
element of the elliptic Riemannian space for constructing
the space of interpretation RE. The basis for such a choice
is the fact that Euclidean geometry (R2) takes place on
SK.
D. Hilbert wrote about it that the greatness of W. Clif-
ford’s discovery is that the Euclidean plane “in the
small” is present in a closed and restricted curvilinear
space. SK is isomeric to a Euclidean rectangle or rhomb
with identified opposite sides, what leads us to an ordi-
nary Euclidean torus.


2
R
EK
I
ST, (2)
where T2 is a 2D torus belonging to the Euclidean space.
But with that principal difference, that a torus loses its
geometrical independence in the space of interpretation
and becomes a carrier of the SK properties. That is, in the
space of interpretation a torus is a very surface on which
Euclidean geometry is fulfilled and well-known groups
of movements of a Euclidean torus are more not applica-
ble to it. To operate with a torus in the space of interpre-
tation one should follow other rules. In RE the motions of
a torus are rotations. At the same time, using the fact that
RE is “arranged” in a Euclidean space, it is possible to
carry out sections of RE by a Euclidean plane and, in such
a way, to study properties of structures in the space of
interpretation. It is extremely important that the Clifford
surface is a carrier of Euclidean geometry, then in RE on
a torus (or on systems of tori) all the physical laws show
themselves in the same form and with the same content,

Geometrical Modeling of Crystal Structures with Use of Space of Elliptic Riemannian Geometry 528
as on the Euclidean plane and in the space. The differ-
ence is that an arc lying on a torus is used instead of a
segment of a Euclidean straight line. For example, in
Coulomb’s law L—an arc on a torus is used in RE instead
of r.
The existence of systems of parallel straight lines of
the Riemannian space on the Clifford surface (SK) leads
to the presence of groups of parallel transports, both on
the Clifford surface and generally in the Riemannian
space (the so-called Clifford’s parallels), and, so, of
groups of translations. It is important to remember that
these groups are realized only on SK, but not on planes of
the Riemannian space. In RE these groups show them-
selves rather originally and will be described below. Im-
ages of translations on the Clifford surface are expressed
in RЕ as a rotation of the torus about own axes, and are
defined by the group where

12
,
ll
TTT
HHH

,1
l
T
H
is a
subgroup of the rotation about the axis l1, 2
l
T
H
is a sub-
group of the rotation about the axis l2, that is, as a slip on
itself.

,
R
E
ST
I
HH (3)
where S
H
is a translational group formed from sub-
groups of the paratactic displacements of SK.
Translations of the Clifford surface itself in the Rie-
mannian space are expressed in RЕ as a rotation of the
torus about own generatrices.
  
2.
R
ESK T
I
HS HT (4)
Different crystallographic axes of symmetry (from l2
up to l6) are considered on different Clifford surfaces,
what is expressed in RE as an application of tori with dif-
ferent ratios of the interior and exterior radiuses. When
unfolding tori, it shows itself in the form of rectangles
with different lengths of sides and with different angles
between their diagonals (for the axis l3, for example, an
angle between diagonals is taken to be equal to 60 or 30
degrees, for the axis l4 this angle is equal to 45 degrees,
with corresponding side lengths of the rectangle of an
unfolding).





2,
ii
ml R
ET KTii
IH SHTrR, (5)
where ri and Ri are the interior and exterior addresses of a
torus, respectively; i
l
T
H
are subgroups of the rotation of
T2; i
m
S
H
are subgroups of the rotation of SK; i is an or-
der of symmetry.

,
R
E
ST
I
OO (6)
where is a subgroup of the

 
2,
O
TT kk
OHTrR
 
rotation of a torus, the ratio k
r
k
m
Rn

the radiuses.
ace of interpretation RE (Riemannian in
Eu
being correct for
By the sp
clidean) we shall call a totality of all points A being
equivalent to a point O through which there passes a to-
rus—


2,
O
kk
TrR with the ratio of the internal and exte-
rior ra equal to m : n, on all possible transla-
tions of this torus, interpreted as it was pointed out
above.
diuses being


,,
ETT
RHO (7)
where T
H
f th
is a translational subgroup;
graphy and ma-
te
interpretation there exist three families
tic field of a charge is restricted in sizes,
res of crystal structures in RE is pos-
si
el of
a
T
O
ce
is a sub-
group oe rotations that form a subspaof RE. We
shall call the point О by the center of the space of inter-
pretation. It is easy to show that the space of interpreta-
tion is restricted, closed, and continuous. A select of the
value of the ratio of the radiuses of a torus will be de-
fined for a given model by a type of symmetry of a crys-
tal structure viewed. It is convenient to study the geo-
metrical and structural features of objects in RE by means
of sections of the space of interpretation by Euclidean
planes. However, the most important property of the
space of interpretation is that on a torus in RE we have
the right to consider physical laws in their normal
Euclidean interpretation, except for a replacement of
Euclidean segments by arcs of a torus.
For problems of mineralogy, crystallo
rial science Coulomb’s law is of heightened inter-
est—thanks to its simplicity and the fact that when inter-
preting it the features of RE show themselves most
brightly, namely:
 In the space of
of the shortest lines (rounds with the ratio of diame-
ters being equal 1:2:3) each of which becomes a fam-
ily of lines of force of an electrostatic charge Q. The
electrostatic lines of force do not start from the charge
Q, and do not end at infinity, but touch a surface of
the charge, and close up at some distance from it.
This distance is calculated using usual trigonometry
formulas;
 An electrosta
closed, and continuous. At some distance from a
charge Q its electrostatic field is already absent. This
distance is called a radius of the field of a charge Q
and denoted by Rp. It should be noted that an electro-
static field of a charge Q does not occupy the entire
space of interpretation completely. Thus two different
charges, Q1 and Q2, can interact or not, depending on
a distance between them, as well as on their own lin-
ear dimensions.
Studying the featu
ble in sections by its Euclidean plane in two ways:
Case 1: Symmetry of a structure is known. A mod
crystal structure is considered in the form of point sys-
tems where points simulate a distribution of centers of

Geometrical Modeling of Crystal Structures with Use of Space of Elliptic Riemannian Geometry529
structure is unknown, or a
str
l lattice system in a
Eu
here is the othe
si
tures in
In mescribing the
to mod-
el
n el-
lip
odeling of lattice structures of a given
structures of
ng of microstructures of crystals in
nt for
ob
e chemical composition of an explored
st
ture of electrostatic components of
pa
structing sublattices for
ea
atoms in lattice points—the so-called R-systems which
are computer-simulated using a special program. A sec-
tion by the Euclidean plane is carried out either perpen-
dicularly to the axis of symmetry of the structure studied,
or at an angle interesting us.
Case 2: Symmetry of a
ucture has been badly studied from the point of view
of symmetry. Under these circumstances the task be-
comes complicated and is solved in a few stages, what
will be considered below (Item 1.2).
The principal difference of an idea
clidean space and in RE consists in the following: in a
Euclidean space an ideal crystal has to be either infinite
large-sized or infinitesimal. An ideal Euclidean crystal
has no center of symmetry, zonality, and sectoriality, and
is not faceted. The question about the faceting of an ideal
crystal is solved with the help of introducing different
sets of the so-called “boundary conditions”. Simply
speaking, the ideal Euclidean model of a crystal does not
possess those structural features that are characteristic for
real crystals, except for a fragmentary coincidence to
restricted fragments of a plane lattice. In the history of
mineralogy, crystallography, and geology generally, no
real crystal coinciding on its own structural and symme-
try characteristics with its ideal Euclidean models has
been met. The fact is well-known, but somehow slips
attention of researchers all the time.
In the space of interpretation RE tr
crystal in accordance with its Fedorov group of sym-
metry, realized in the elliptic Riemannian space with
the involvement of visualizing the model construc-
tions. Building on data obtained when modeling point
systems with a given Fedorov group, it is possible to
form judgments about the morphology of a structure,
clustering, and a type of zonality, and to make suppo-
sitions of different types of anisotropy;
 Theoretical modeling of a family of
tuation. An ideal crystal in the space of interpretation is
restricted in sizes, has a certain shape and symmetry, is
zonal and sectorial, and also possesses the center—that is,
it possesses practically a complete set of the structural
and symmetry characteristics which the real crystal of a
mineral has. If one takes into account that both the radius
of an electrostatic field Rp and linear dimensions of the
space of interpretation RE are calculated in accordance
with values of the ionic radius Ri and atomic radius Ra of
a given substance, we can always estimate both real sizes
of microcrystalline blocks and distances at which there
are electrostatic interactions between real ions.
2.2. Principles of Modeling Crystal Struc
Elliptic Riemannian Geometry
odern structural examinations, when d
organization and processes of the growth of a crystal
structure, information about the type of a space in which
an explored process being watched is not enough used
[11-14]. The examinations of different non-Euclidean
methods of describing elements of a crystal lattice [4] are
the foundation of the suggested theoretical approach to
modeling crystal structures under the conditions of Rie-
mannian geometry. In order to achieve results the inter-
pretation of the geometrical objects (SK, F-groups, and
symmetries) in Riemannian geometry is used. In a
three-dimensional Euclidean space a 2D torus 2
T (see
formula 2), on which the basic geometrical transrma-
tions (lattices, elements of Fedorov groups) are consid-
ered, corresponds to the Clifford surface (SK).
The basic difference from existing approaches
fo
ing consists in a statement according to which the or-
ganization of a lattice structure happens in accordance
with a certain F-group (() Ф
R
E
IF) operating in the
Riemannian space V4. An a in a model of the
lattice system is considered as a point site, and point sys-
tems are studied in the initial stage without regard to the
chemical features of atoms. By using the approach under
consideration, modeling the cluster organization of mi-
crostructures of oxides is carried out, as well as practical
applications aimed at perfecting crystalline materials and
improving their physical properties are developed.
General principles of modeling crystal structures i
tom or ion
tic Riemannian geometry may be reduced to the fol-
lowing:
 Theoretical m
electrostatic fields of ions of elements having partici-
pated in the formation of lattices of a given crystal;
constructing the potential surfaces answering to
minimum energy;
 Theoretical modeli
the model sections perpendicular to axes of symmetry,
with regard to: a composition, symmetry, a structure
of electrostatic fields of ions and their systems, the
principle of closest packing; as well as crystallo-
graphic analysis and interpreting data obtained.
Thus a general procedure of computing experime
taining a model of a crystal structure of a necessary
chemical composition and structure adds up to the fol-
lowing stages.
Stage 1: Th
ructure is detected.
Stage 2: The struc
rameters of ions and atoms constituting the structure of
a given substance is computed.
Stage 3: Regularities of con
ch of elements composing a given structure are re-
vealed, according to the series of crystallochemical activ-
ity [15].

Geometrical Modeling of Crystal Structures with Use of Space of Elliptic Riemannian Geometry 530
Stage 4: Upon the Clifford surface’s unfolding a frag-
m
appropriate to-
ru
ent of the sublattice is constructed using the computa-
tions of the parameters of electrostatic components of a
model for each ion, and then the incorporation of sublat-
tices of the rest of atoms and ions is conducted in accor-
dance with the computed parameters, according to the
series of crystallochemical activity [15].
Stage 5: By the unfolding obtained an
s is folded, and all the necessary transformations (par-
allel translations, rotations about axes of symmetry, etc.)
are applied to it, according to the scheme for the inter-
pretation
R
E
I
.
Stage 6: For visualizing the constructions a necessary
se
rithm
in the examination of properties and
ction of the space RE by a Euclidean plane is con-
structed, where the features of a studied structure are
considered.
2.3. F-Algo
The important place
features of the organization of a crystal structure in the
space RE is occupied with constructions of point systems
with the use of special computational algorithms for
solving of tasks of the visualization and interpretation of
constructed models. For modeling lattice systems in the
space RE an algorithm has been developed, with the help
of which constructions of lattices are produced with regard
to the fact that for each Fedorov group Ф of the Euclid-
ean space R3 in the Riemannian space there is an appro-
priate F-group satisfying to the condition ()
R
E
IF

.
For the proof it is enough to take the pacerojective sp
RP
and
3 and to use the homeomorphism theorem for the
groups SO(3) and SU(2) [16]. From an epimorphism
π: SU(2)  SO(3) it is possible to obtain F-groups, as
subgroups of the group SU(2). The so-called binary
groups arise:

*1
π ,
nn
DD

*1
π,
nn

*1
π,
nn
TT



*1
π,
nn
QQ


I
I


a binary group of a dihedral, a binary group of a tetrahe-
lgorithm suggested in this work defines rules for
co
dron, a binary group of an octahedron, and a binary
group of an icosahedron. The binary groups, as well as
orthogonal representations, in whole, arise naturally in
describing a physical system with a spin and in calculat-
ing characteristics of gravitational fields in Riemannian
spaces.
The a
nstructing point systems for a given F-group and there-
fore will be denoted by F-algorithm. The given
F-algorithm, realizing the translational subgroup S
H
in
the Riemannian space when interpreting


S
K
S

R
E
IH


2T
H
T, will describe a representation b
point on a Euclidean plane:
y the fongllowi
rule for a

32π
exp ,
s
li
rl


 1
1
1, ,
s
s
n
n
  (8)
1. F
rr

G (9)
As parameters of a model the
ac
following variables were
cepted: GF is a matrix of a subgroup of the rotations
T
O induced in a section by a given F-group, where


RF
E
I

; rs is the radius of the surface SK; t r is the
appropriate torus 2
T, where

R
radius of an
E
st
I
rr

; n is
an amount of the points lyingn the sece sur-
face SK.
A set of points computed by the F-algorithm (8) or-
ga
otion of th
nizes a system of the points on a plane, which we shall
denote by K-system. The parameters defining a K-system
are: a Fedorov group Ф, F-groups, and a basic axis of
symmetry li. A K-system can be determined with the help
of its constituent sets i
n
T and represented in the follow-
ing form:


123
,,
nn n
K
TT T, (10)
where are sequentially generat
i
n
T
ca
ed sets in Figure 1
(for these 6n

), satisfying to the conditions given
below:











222
22221
,
32222
,
,,1,,
,,,,1,,
,,,,1,.
iiit
O
njj jjtn
xy
nkk kktn
xy
yxyrin
Txy xyrxyTin
Txy xyrxyTkn



(11)
A set of points computed by the F-algorithm (9) or-
a
1
ni
Tx
g nizes a system of the points on a plane, which we shall
denote by R-system. This implies that the generation of
an R-system is carried out by performing a group of the
transformations


2T
H
T over a K-system.



2TTK. RH (12)
The initial forms of the organiz
ar
E
ation of real crystals
e R-systems. The real structure of a crystal is supposed
to be consisting of rows of particles, integrated into a
system, and to have concrete sizes of the space of inter-
pretation. With the help of the apparatus of elliptic Rie-
mannian geometry, a distribution of atoms and a filling
of the crystalline space can be interpreted as a compact
locally Euclidean set. The misorientation and displace-
ment of R-systems are accompanied by the appearance,
in the integrated space of a crystal, of blocks and bound-
ary spaces separating them [15].
The process of the organization of a crystal structure in
R consists in sequential introducing new particles into
consideration, arranged at the shortest distances (put on a
torus) from fixed ones in accordance with a given Fedorov

Geometrical Modeling of Crystal Structures with Use of Space of Elliptic Riemannian Geometry531
(a)
(b)
(c)
Figure 1. Stages of constructing a K-system. A sequence of
the formation of the sets: (a)b; (c)
hoizon of a lat-
ce in RE can be presented as a multistage process in
n number of the
la
of a crystalline polyhe-
dr
along geodetic lines of the elliptic space, spreading the
1
T; (
6)2
6
T3
6
T.
group, up to the faceting. Tus the rganati
ti
which bonding of chemically responsive particles is un-
der way, beginning from the zero point.
On a K-system, nodes are connected by arcs of circles
and arranged from each other at a certai
ttice periods (E). An ideal crystal is usually constructed
by the multiplication of a finite number of atoms by all
the transformations of some Fedorov group, but such a
construction of the ideal crystal is not related to natural
causes of the crystallization [4].
The organization of a lattice system in the space of in-
terpretation RE, up to the faceting
on, consists of the structurally-forming (Figure 2(a))
and structurally-filling (Figure 2(b)) stages, each of
newly fixed particles behaving like a new center of the
organization of the lattice. The realization of bonds passes
(a)
(b)
Figure 2. (a) Structurally-forming (), and structur-
ally-filling stages of the organizationtal stcture;
(b) The sets (have bonstr.
apec Riemannian
ace.
degrees of order of atoms inside a crystal and at
its
res in the space
developed,
ons of crys-
1
12
T
of a crys
ucted
ru
2
12
T,3
12
T) een c
forces of long-range interaction to the whole closed re-
gion, what is scific feature of an ellipti
sp
The noted features of a distribution of lattice points on
a R-system are in good conformity with really observed
different
near-surface layers, different reticular densities of
particles on different areas of the same face. The con-
structed model possesses all the attributes of a real crys-
tal: a center, an exterior faceting, symmetries of a certain
Fedorov group, finite sizes, and zonality.
3. Visualization of Lattice Systems
For computer simulation of crystal structu
RE an rСrystal software package has been
allowing to conduct the visualization of secti
tal structures and to construct models of the electrostatic
components of parameters of ions. There is the possibil-
ity of inputting various types of crystal structures with
the use of a special technique of coding. The software
package for modeling point systems uses the F-algorithm

Geometrical Modeling of Crystal Structures with Use of Space of Elliptic Riemannian Geometry 532
for visualizing constructions and the scheme for the in-
terpretation
R
E
I
of geometrical objects on the Clifford
surface in the Riemannian space.
Examples of the computations of point systems with
the use of th-algorithm have been given for modeling
the symmetry axes: l3 (Figure 4),
e F
l4 (Figure 5), and l6
(F
d sections perpendicularly to the axis l6,
igure 3).
It is obvious from Figure 3(a) and Figure 3(b) that
the character of the distributions of the point systems, on
the constructe
essentially differs in a central region. If the point system
in Figure 3(a) has a homogeneous distribution, then for
the point system in Figure 3(b) a block structure is
(a)
Figure 4. The organization of a lattice system in the section
plane, perpendicularly to the axes l3, for a model of the
trigonal system.
Figure 5. The organization of a lattice system in the section
plane, perpendicularly to the axes l4, for a model of the cu-
bic system.
on in the space and have a centre and a zonal
ructure.
ures 7 and 8) and a series of its polymorphic
m
clearly seen. All the constructed point systems fill a re-
stricted regi
st
With the use of the rCrystal software package the com-
plex modeling of the crystal structures SiO2 (Figure 6),
Al2O3 (Fig
odifications α-, β-, θ-, and γ-Al2O3 [17,18] has been
carried out. A method of modeling mesoatomic ensem-
bles, clusters and crystal structures, permitting to explore
the geometrical properties of oxide systems, has been
(b)
Figure 3. The homogeneous (a) and block (b) structures (an
ideal system) in a section perpendicular to the axes l6.

Geometrical Modeling of Crystal Structures with Use of Space of Elliptic Riemannian Geometry533
po-
ne
tiocharge distribution on a surface
developed. On the basis of the model computations a
minimum structural element Al4O6 has been selected,
parameters of which were computed in the space RE. Us-
ing the above mentioned approach a model of the crys-
talline structure Al2O3 has been computed. The geomet-
rical configuration of a micropolyhedron Al4O6 and a set
of the external physicochemical conditions (a structure of
the electromagnetic field, thermodynamic parameters,
crystallophysical parameters) define methods of packing
of the micropolyhedrons in different motifs in accor-
dance with the principle of closest packing (Figures 7(а)
and (b)). The structure of an electrostatic field modeled
in the space RE, being formed by the structural element
Al4O6, defines possible methods of integrating into a
macrostructure in accordance with the most probable
joining mechanism.
4. Computation of Pair Interaction
Potentials When Modeling Structures
in the Space RE
In the space RE the models of the electrostatic com
nts of parameters of ions in the case of pair interac-
ns with regard to a
have been constructed for the following ions presented in
Table 1. When computing, a model of the charged
spheres with different charge distributions on a surface
was used. The suggested approach uses the scheme ,
R
E
I
what allows to study the features and character of the
interaction of elements in a modeled crystal structure,
and to explore regularities of its formation.
When computing the geometrical parameters of poten-
tials of the interatomic interaction, it was supposed that
the interaction occurs under the conditions of the elliptic
O
Si
Figure 6. The model of the crystal structure SiO2. The sec-
tion arranged perpendicularly to the axis l3 has been shown.
closed Riemannian space V4. The structural features of an
electrostatic field in the Riemannian space, considered
for the case of interacting the unlike charges of ions, im-
pose the special conditions which lead to the formation
of coherent states and to the formation of local closed
(a)
(b)
Figure 7. The motif I1 of the model of the crystal structure
Al2O3, satisfying to the principle of closest packing (a), the
corundum motif I2 (b); the models has been presented in a
projection on the plane [0001].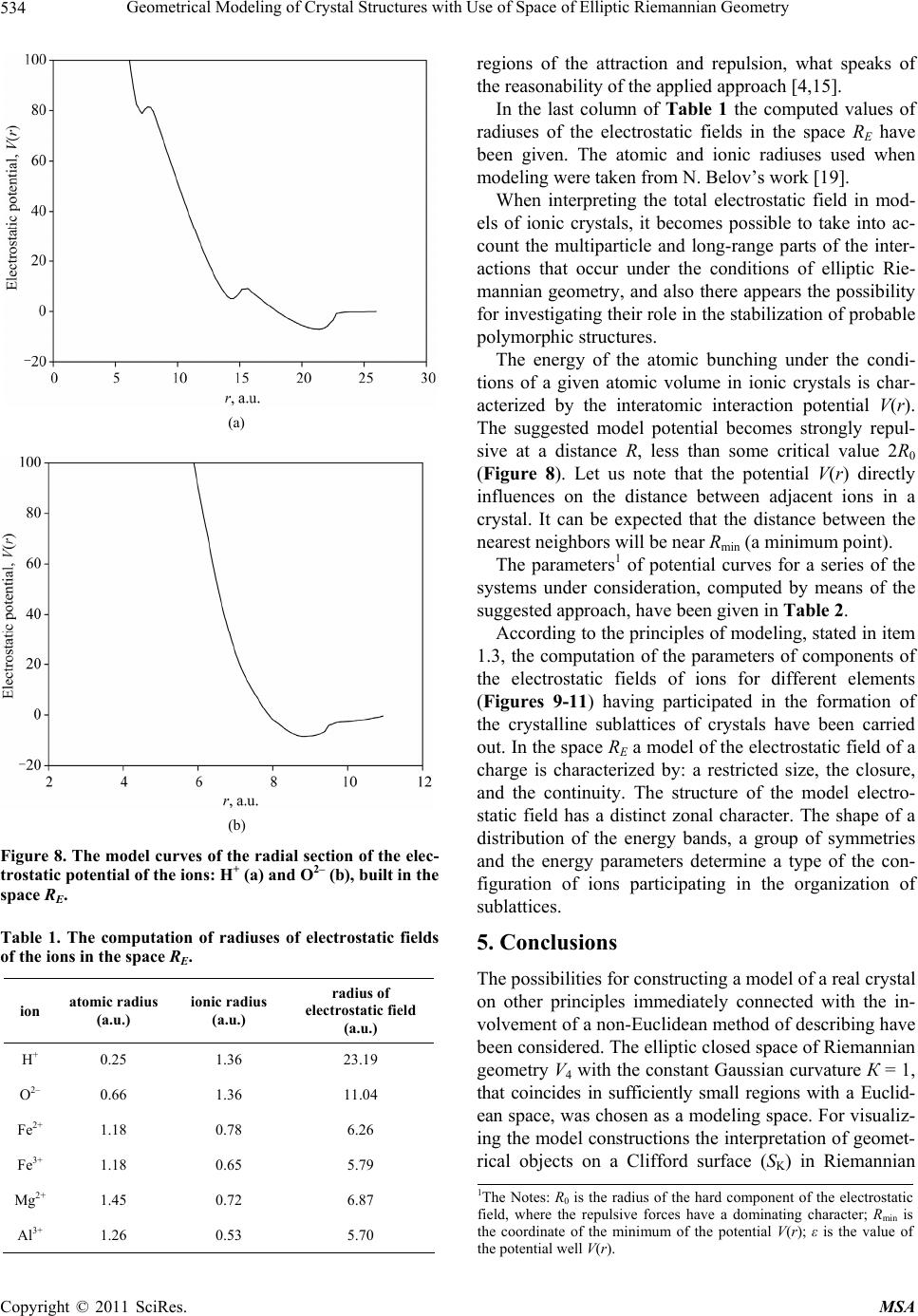

Geometrical Modeling of Crystal Structures with Use of Space of Elliptic Riemannian Geometry 534
regions of the attraction and repulsion, what speaks of
the reasonability of the applied approach [4,15].
In the last column of Table 1 the computed values of
radiuses of the electrostatic fields in the space RE have
been given. The atomic and ionic radiuses used when
modeling were taken from N. Belov’s work [19].
When interpreting the total electrostatic field in mod-
els of ionic crystals, it becomes possible to take into ac-
count the multiparticle and long-range parts of the inter-
actions that occur under the conditions of elliptic Rie-
mannian geometry, and also there appears the possibility
for investigating their role in the stabilization of probable
polymorphic structures.
The energy of the atomic bunching under the condi-
tions of a given atomic volume in ionic crystals is char-
acterized by the interatomic interaction potential V(r
The suggested model potential becomes strongly repul-
on the distance between adjacent ions in a
ntial curves for a series of the
systems underated byf the
su teavn
According to the principles of modeling, s
1.3e comion of the eters of coents of
the electrostatents
(Fres 9-1aving par in the tion of
thystallinblattices ostals have
out. I the space RE a model of the electrostatic field of a
charge is chrized by: tricted size, the closure,
ae cony. The stre of the moelectro-
static field has a distinct zonal character. The shape of a
diution nergy b, a group ofmetries
ation of
su
rystal
on
s the interpretation of geomet-
ric
(a)
).
sive at a distance R, less than some critical value 2R0
(Figure 8). Let us note that the potential V(r) directly
influences
crystal. It can be expected that the distance between the
nearest neighbors will be near Rmin (a minimum point).
The parameters1 of pote
der consi
d aph, h
ion, comput
e beiven i
means o
Table 2.
tated in item
ggesproacen g
, thputatparammpon
ic fields of
1) h
ions for different
ticipated
elem
forma
igu
e cre suf crybeen carried
n
aractea res
nd thtinuitucturdel
stribof the eands sym
(b)
Figure 8. The model curves of the radial section of the elec-
trostatic potential of the ions: Н+ (a) and O2– (b), built in the
space RE.
Table 1. The computation of radiuses of electrostatic fields
of the ions in the space RE.
ion atomic radius
(a.u.)
ionic radius
(a.u.)
radius of
electrostatic field
(a.u.)
and the energy parameters determine a type of the con-
figuration of ions participating in the organiz
blattices.
5. Conclusions
The possibilities for constructing a model of a real c
other principles immediately connected with the in-
volvement of a non-Euclidean method of describing have
been considered. The elliptic closed space of Riemannian
geometry V4 with the constant Gaussian curvature К = 1,
that coincides in sufficiently small regions with a Euclid-
ean space, was chosen as a modeling space. For visualiz-
ing the model construction
H+ 0.25 1.36 23.19
O2– 0.66 1.36 11.04
Fe2+ 1.18 0.78 6.26
Fe3+ 1.18 0.65 5.79
Mg2+ 1.45 0.72 6.87
Al3+ 1.26 0.53 5.70
al objects on a Clifford surface (SK) in Riemannian
1The Notes: R0is the radius of the hard component of the electrostatic
field, where the repulsive forces have a dominating character; Rmin is
the coordinate of the minimum of the potential V(r); ε is the value o
f
the potential well V(r).

Geometrical Modeling of Crystal Structures with Use of Space of Elliptic Riemannian Geometry535
Table 2. The parameters of potential curves of the intera-
tomic interaction in the space RE.
bond type R0, Rmin, depth radius of electrostatic
(a.u.) (a.u.) (ε) field (a.u.)
[H+] – O2– 17.96 20.81 –6.14 23.19
[O2–] – Fe2+ 7.88 8.76 –8.51 11.04
[O2–] – Fe3+ 7.88 8.92 –8.81 11.04
[O2–] – Al3+ 7.98 8.97 –8.90 11.04
[Fe2+] – O2– 5.07 5.68 –5.81 6.26
[Fe3+] – O2– 4.71 5.51 –16.22 5.79
[Mg2+] – O2– 5.60 6.24 –6.32 6.87
[Al3+] – O2– 4.66 5.44 –17.41 5.70
Figure 9. The equatorial section of
3+
the model of the electro-
static potential of the ion Al. The computation has been
carr the RE.
ied out inspace
Figure 11. The equipotential picture of the electrostatic field
of the ion O2– relatively the ion H+. The frontal section.
geometry with the help of a 2D torus in a Euclidean
space E3 is used. The process of the organization of a
crystal structure in the space of interpretation RE is pre-
sented as a multistage process consisting in sequential
introducing the point systems into
consideration, each point of whic
accordance with a given Fedorov group, beginning from
a zero point and up to the faceting of a crystal, each of
newly fixed point behaving like a new center of the or-
ganization of the lattice. Properties of the internal space
of a real crystal, such as zonality, boundedness in sizes
(finiteness), sectoriality and the occurrence of a center,
are naturally deduced from properties of the modeling
space. The main characteristic of improvements in the
suggested model constructions is that the local changes
The developed F-algorithm for constructing crystalline
lattice systems ensures a computation of 2D sections of
models of point systems, arranged perpendicularly to the
symmetry axes l3, l4, and l6. As an example of the reali-
zation of the developed principles of modeling, the
computations of components of the electrostatic fields of
the ions Al3+, O2–, Fe2+, and Mg2+, having participated in
the formation of the crystalline sublattices of α-, β-, θ-,
and γ-Al2O3, have been presented. The linear parameters
of crystal lattices, obtained from the model computations,
are connected with the character of their constituent at-
oms and can be used to determine a type of chemical
bonding between them.
The suggested approach can be used for computing the
as for the development of practical


2T
RHTK
h is fixed on a torus in
of structural features, as well as curved regions (defects),
can be more completely taken into account.
geometrical parameters of the cluster organization of
nanostructures of oxides and many other nonequilibrium
materials, as well
Figure 10. The equipotential picture of the electrostatic field
of the ion H+ relatively the ion O2–. The frontal section.

Geometrical Modeling of Crystal Structures with Use of Space of Elliptic Riemannian Geometry 536
applications connected with improving the structural
characteristics of crystalline materials.
REFERENCES
[1] R. V. Galiulin, “The Geometrical Theory of Crysta
tion,” Crystallography Reports, Vol. 43, No. 2, 1998, pp.
366-347.
[2] S. van Aert, K. J. Batenburg, M. D. Rossell, R. Erni and G.
van Tendeloo, “Three-Dimensional Atomic Imaging of
Crystalline Nanoparticles,” Nature, Vol. 470, 2011, pp.
374-377. doi:10.1038/nature09741
[11] H. A. R. Aliabad and S. R. Ghorbani, “Structural and Spin
Polarization Effects of Cr, Fe and Ti
tronical Properties of α-Al O by Firs
Elements on Elec-
2 3t Principle Calcula-
tions,” Journa ol. 2, No. 3, 2011,
pp. 158-161. d 24
l of Modern Physics, V
oi:10.4236/jmp.2011.230
(0001) α-Cr2O3 Templates,” Surface Science,
lliza-
[12] J. Z. Sun, T. Stirner and A. Matthews, “Structure and
Electronic Properties Calculation of Ultrathin α-Al2O3
Films on
Vol. 601, No. 21, 2007, pp. 5050-5056.
doi:10.1016/j.susc.2007.09.004
[13] M. M. Zhong, X. Y. Kuang, H. Q. Wang; H. F. Li, Y. R.
Zhao, “Density Functional Study
[3] A. Authier, “International Tables for Crystallograph
D, Physical Properties of Crystals,” Chapter 1.2, Kluwer
Academic Publishers, Dordrecht, 2003.
[4] S. V. Rudnev, “Application of Elliptic Riemannian Ge-
ometry to Problems Crystallography,” Computers and
of the Structural and
tween Chemistry
Electronic Properties of Tetra-Aluminum Oxide λ
n 4
Al O (3
≤ n ≤ 8, λ = 0, –1) Clusters,” Molecular Physics: An In-
ternational Journal at the Interface be
y: Vol.
and Physics, Vol. 109, No. 4, 2011, pp. 603-612.
doi: 10.1080/00268976.2010.542777
[14] R. Ahuja, J. M. R. Ahuja, J. M. Osorio-Guillen, J. Souza
de Almeida, B. Holm, W. Y. Ching and B. Joh
Mathematics with Applications, Vol. 16, No. 5-8, 1988,
pp. 597-616. doi:10.1016/0898-1221(88)90249-0 ansson,
984/16/16/013
“Electronic and Optical Properties of γ-Al2O3 from ab
Initio Theory, ” Journal of Physics: Condensed Matter,
Vol. 15, No. 16, 2004, pp. 2891-2898.
doi: 10.1088/0953-8
[5] B. S. Semukhin, A. N. Sergeev and S. V. Rudnev
to Study of Crys
,
“Non-Euclidean Interpretation of the Structures of Crys-
talline Materials,” Crystallography Reports, Vol. 4, No. 5,
1999, pp. 738-741.
[6] S. V. Rudnev and V. A Ermolaev, “On Application of
Elliptical Riemannian Geometrytalline
Structure,” Proceedings of Geometry, Vol. 25, 1985, pp.
113-121.
[7] B. S. Semukhin, S. V. Rudnev and R. V. Galiulin, “Ap-
plication of Riemann Geometry to Structures of Nano-
and Macrocrystals,” Crystallography Reports, Vol. 53,
No. 4, 2008, pp. 541-544.
doi:10.1134/S1063774508040019
[8] S. V. Rudnev, A. N. Sergeev, V. G. Bamburov and G. P.
Shvykin, “Geometrical Modeling of Superplastic Con-
structional Ceramics Structure,” Doklady Chemistry, Vol.
341, No. 4, 1995, pp. 589-501.
[9] S. A. Bogomolov, “An Introduction to Non-Euclidian
Geometry,” GTTI, Moscow-Leningrad, 1934.
brovin, A. T. Fomenko and S. P. Novikov,
, V. A. Er-
g Process of Structural
d V. I. Vereshagin, “New
Refracto-
[15] S. V. Rudnev and А. N. Sergeev, “ICS Simulation of
Crystal Mineral Grouth and Deformation,” TGU Tomsk
State University, Tomsk, 1994.
[16] B. A. Du
“Modern Geometry-Methods and Applications: Part I:
The Geometry of Surfaces, Transformation Groups, and
Fields,” Springer-Verlag, New York, 1991.
[17] А. P. Klishin, A. N. Zakutaev, S. V. Rudnev
molaev and T. A. Habas, “Modelin
Transformations in Al2O3 at Magnetothermal Treatment,”
Constructions from Composite Materials, Vol. 1, 2008,
pp. 12-17.
[18] А. P. Klishin, S. V. Rudnev an
Technological Approaches of Reception Alumina Materi-
als with Usage of Magnetothermal Treatment,”
ries and Technical Ceramics, No. 6, 2009, pp. 30-34.
[19] N. V. Belov, “Structural Crystallography,” USSR Acad-
emy of Sciences, Moscow, 1952.
[10] W. K. Clifford, “Preliminary Sketch of Biquaternions,”
Proceedings of the London Mathematical Society, Vol.
S1-S4, No. 1, 1871, pp. 381-395.
doi:10.1112/plms/s1-4.1.381