Journal of Applied Mathematics and Physics
Vol.03 No.02(2015), Article ID:53709,5 pages
10.4236/jamp.2015.32039
Spectral Imagers with Linear Detector Imager Systems Based on Spectrum Compressed
Xiaoming Zhong, Huang Li
Beijing Institute of Space Mechanics & Electricity, Beijing, China
Email: xiaoming.zhong@163.com


Received 14 December 2014

ABSTRACT
Traditional spectral imagers require 2-dimensional detectors. We present a new method to implement spectral imagers with linear detector imager systems based on spectrum compressed. Using 1-dimension detectors instead of 2-dimension detectors to get 3-dimensional data cubes, the spectral imagers could get both the spectral information and the spatial information of each ground object. By the method of characteristics decoupling, we make high precision reconstruction of compressed data. Theoretical analysis and simulations show that it not only ensures the imaging quality but also reduces the dimension of the detectors and complexity of imaging system greatly.
Keywords:
Linear Detector Imager, Spectrum Compressed, Characteristics Decoupling

1. Introduction
In most push-broom imaging spectrometers, they employ split structures. This will cause the spatial resolution decreasing. We present a new approach to implement computational spectral imaging, bring forward research on the mechanism of spectral imagers with linear detector imager systems on spectrum compressed, present a detailed theoretical analysis and give a simulation on this algorithm.
2. The Traditional Push-Broom Imaging Spectrometer’s Principle
Push-broom imaging principle of scanning imaging spectrometer is shown as Figure 1 shows: through a slit in the direction parallel to the slit dimension and imaging in the vertical slit direction to obtain a two-dimensional target imaging [1].
3. Spectral Imaging with Linear Detector Imager System Model
3.1. System Introduction
Spectral imager with linear detector imager systems are based on the traditional dispersive spectral imaging
Figure 1.Traditional push-broom imaging spectrometer.
technology. The code template has a special mathematical code form. The spatial information and spectral of the original target can be modulated with the code template, using the theory of compressive sensing. We can reconstruct one-dimensional special information and one-dimensional spectral information from the map of aliasing imaging. We can obtain the two-dimensional special information with the push-broom imaging model.
As Figure 2 shows, the system consists of (1) an objective lens, (2) a coded aperture, (3) relay lens, (4) dispersion prism, and (5) a monochrome linear charge-coupled device (CCD) detector. The objective lens images the scene on to the plane of the coded aperture.
3.2. Code Process
The spectral imager with linear detector imager system realizes a single shot compressive spectral imaging system. As Figure 3 shows, it encoded both 1D spatial and 1D spectral information of objects through an aperture code projection that is captured after it propagates through a dispersive element, a linear detector then collects all light passing through the aperture and the dispersive element. It is important to emphasize that the code
aperture pattern remains fix in the sampling process. Suppose that the scene or object is represented by 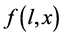 [2], where
[2], where 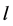 is the wavelength and
is the wavelength and  correspond to the spatial position, in discrete form it is denoted as
correspond to the spatial position, in discrete form it is denoted as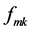 . Suppose that the code pattern is
. Suppose that the code pattern is  [3]. The term
[3]. The term 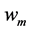 takes into account all possible noise source. Then the
takes into account all possible noise source. Then the
signal in front of the array detector can be expressed by (1) [4].
Example
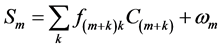 (1)
(1)
3.3. The Reconstruction Algorithm
TwIST (Two-step Iterative Shrinkage Thresholding) is an algorithm framework introduced by Bioucas-Dias and Figueiredo [5]. In the context of image reconstruction for a CASSI system, in this paper, we reconstruct the image
Figure 2. Spectral imagers system composition.
Figure 3. Spectral imagers on spectrum compressed.
of spectral imagers with linear detector imager system with TwIST. TwIST describes a solution as the solution to the generalized non-linear, unconstrained minimization problem:
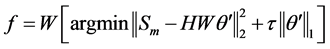 (2)
(2)
Here the linear operator 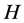 represents the system forward model. Reconstruction of
represents the system forward model. Reconstruction of 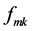 is attained by solving the optimization problem. The first term minimizes the difference between the model and the measurement
is attained by solving the optimization problem. The first term minimizes the difference between the model and the measurement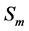 . The variable tau > 0 controls the level of sparsity attained in the reconstruction. The sparser the source
. The variable tau > 0 controls the level of sparsity attained in the reconstruction. The sparser the source , the better the performance of the reconstruction algorithm. In this work, the CS reconstruction algorithm was used to solve the Equation (2). The above procedure tries to recover the overall data cube with only one measurement and hence it often yields a low SNR output performance.
, the better the performance of the reconstruction algorithm. In this work, the CS reconstruction algorithm was used to solve the Equation (2). The above procedure tries to recover the overall data cube with only one measurement and hence it often yields a low SNR output performance.
Before recovering spectral data, spectra data should be reprocessed to be normalized. Normalized data can be directly used algorithm for recovering. Restoration of the accuracy of the results depend on the end of the iteration condition.
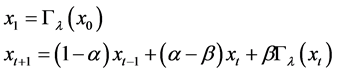 (3)
(3)
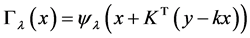 (4)
(4)
Before restoration, we need to set two parameters, the balance to the noise function and the end of iterative threshold tol.
The termination function in defined as

The termination function is tol. We stop iterativing if
The process for the algorithm is as following:
(1) obtain the parameters


(2) imaging initialization, enter the initial value

(3) deal with 

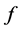

(4) compare 

(5) calculate 






(6) the iteration does not stop until the function is less than tol, if
4. Simulation
The test uses MATLAB to carry on the simulation and reconstruction. The process is as following.
Firstly, from the realistic point of view, we choose online downloading remote sensing image as a simulation of ground targets. As Figure 4 shows, this multispectral database has 33 bands from 400 nm to 720 nm wavelength with a 10 nm step. The image size is 480 × 752 pixels. In the push-broom imaging simulation process, simulation design parameters as follows: the spectral range is 400 - 720 nm; spectrum channel number is 33, detector pixels is 280 × 1, Intercepting 256 × 280 pixels format as the push-broom scene spectrometer remote sensing image above.
Secondly, simulate smashing on the CCD. Different from CASSI, ours system coded model is 1-dimen- sional. Be sure that spectral dispersion direction and detectors arrangement direction is consistent. Linear array detector will get aliasing information, and with the push-broom imaging process, the entire scene information will be obtained. Figure 5 and Figure 6 show the coding model and the smashing result on the CCD.
Finally, with the prior information of the arithmetic coding model and algorithms, we can recover the spectral data cube from the aliasing image data. In our simulation, we choose TwIST for recovering for its accuracy and speed are all well. Figure 7 shows the result of image reconstruction.
Figure 4. Original scene.
Figure 5. Coding model.
Figure 6. Coding imaging.
Figure 7. Reconstructing result.
5. Result
From above, we can see that spectral imagers with linear detector imager system on spectrum compressed can make use of a 1-dimension detector instead of a 2-dimension detector to get a 3-dimensional data cube, which includes both the spectral information and the spatial information of each ground object.
It can decrease the dimensions of the detectors and complexity of imaging system greatly. This work has important and far-reaching theoretical significance and extensive applied values to improve the technique levels of digital remote sensing, and it can satisfy exigent requirements for remote sensing spectral images internally.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 11204014).
Cite this paper
Xiaoming Zhong,Huang Li,Huang Li, (2015) Spectral Imagers with Linear Detector Imager Systems Based on Spectrum Compressed. Journal of Applied Mathematics and Physics,03,267-271. doi: 10.4236/jamp.2015.32039
References
- 1. Shen, Z. (2002) The Principle of the Spaceborne Hyperspectrum Imager. Spacecraft Recovery& Remote Sensing, 23, 28-34.
- 2. Arguello, H. and Arce, G.R. (2011) Code Aperture Agile Spectral Imaging (CAASI). OSA Optics and Photonics Congress, 978-1-55752-914-5.
- 3. Arguello, H., Ye, P. and Arce, G.R. (2010) Spectral Aperture Code Design for Multi-Shot Compressive Spectral Imaging. OSA Optics & Photonics Congress, 978-1-55752-887-2.
- 4. Wagadarikar, A.A., Pitsianis, N.P. and Sun, X.B. (2008) Spectral Image Estimation for Coded Aperture Snapshot Spectral Imagers. Proc SPIE, 7076, 7076-7076-02.
- 5. Bioucas-Dias, J.M. and Figueiredo, M.A. (2007) A New TWIST: Two-Step Iterative Shrinkage, Thresholding Algorithms for Image Restoration. IEEE Trans Image Process, 16, 2992-3004. http://dx.doi.org/10.1109/TIP.2007.909319








