Journal of Applied Mathematics and Physics
Vol.03 No.02(2015), Article ID:53669,6 pages
10.4236/jamp.2015.32026
Radar Cross Section Analysis Using Physical Optics and Its Applications to Marine Targets
Joon-Tae Hwang1*, Suk-Yoon Hong1, Jee-Hun Song2, Hyun-Wung Kwon3
1Department of Naval Architecture and Ocean Engineering, Seoul National University, Seoul, Republic of Korea
2Department of Naval Architecture and Ocean Engineering, Chonnam National University, Yeosu, Republic of Korea
3Department of Naval Architecture and Ocean Engineering, Kojecollege, Koje, Republic of Korea
Email: *jth00@snu.ac.kr, syh@snu.ac.kr, jhs@jnu.ac.kr, khw1@snu.ac.kr


Received 19 November 2014

ABSTRACT
Radar Cross Section (RCS) is one of the most considerable parameters for ship stealth design. As modern ships are larger than their predecessors, RCS must be managed at each design stage for its reduction. For predicting RCS of ship, Radar Cross Section Analysis Program (RACSAN) based on Kirchhoff approximation in high frequency range has been developed. This program can present RCS including multi-bounce effect in exterior and interior structure by combination of geometric optics (GO) and physical optics (PO) methods, coating effect by using Fresnel reflection coefficient, and response time pattern for detected target. In this paper, RCS calculations of ship model with above effects are simulated by using this developed program and RCS results are discussed.
Keywords:
Radar Cross Section (RCS), Kirchhoff Approximation, Multi-Bounce Effect, Response Time Pattern

1. Introduction
The Radar Cross Section (RCS) is concerned with active detection and is an important parameter in stealth design. RCS characteristics are determined by the intrinsic geometric shape. Because modern ships are larger than their predecessors, RCS must be controlled at each design stage for its reduction.
The RCS of simple shaped objects such as a finite plate, a cylinder, and a sphere etc. is represented analytically in [1]. For more complex shaped targets, numerical calculations were needed. The boundary element method (BEM) [2] and finite element method (FEM) [3] were used at low frequency. These methods give accurate results but require a long computer running time. At high frequency, methods such as physical optics (PO) [4], geometric optics (GO) [5], physical theory of diffraction [6] and geometric theory of diffraction [7] provide relatively quick solutions. At present, most numerical calculations of RCS for a target such as a ship at high frequency are based on Kirchhoff approximation [8]. For prediction for RCS of a ship in high frequency range, Radar Cross Section Analysis Program (RACSAN) based on Kirchhoff approximation in PO has been developed.
In this paper, RCS for a ship model is numerically simulated by using this program. Various effects, which are multi-bounce effect in exterior and interior structure by combination of GO and PO methods, coating effect by using Fresnel reflection coefficient, and response time pattern for detected target are considered.
2. Theory
2.1. Physical Optics
The high frequency prediction method assumes that each part of the target scatters energy independently from all other parts, the total energy scattered in the far field is obtained by integrating energy scattered by each part. Therefore, the total RCS of a complex target can be composed of a number of segments, and can be obtained by the summation of the RCS of each segment. The root of the total RCS is estimated by the coherent summation of the RCS of each segment to consider phase information as follows:
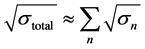 (1)
(1)
where 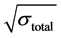 is the root of the total RCS,
is the root of the total RCS, 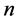 is the number of the segment and
is the number of the segment and 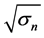 is the root of the RCS
is the root of the RCS
of each segment. The root of the RCS for a polygonal plate can be expressed by the so-called Kirchhoff approximation as follows [9] [10],
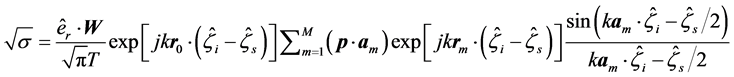 (2)
(2)
where 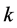 is the wave number,
is the wave number, 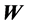 is the polarization vector,
is the polarization vector, 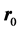 is the position vector of an origin on or near the plate,
is the position vector of an origin on or near the plate, 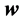 is
is ,
, 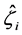 is a unit vector along the incident wave,
is a unit vector along the incident wave, 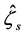 is a unit vector along the reflected wave,
is a unit vector along the reflected wave, 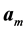 is a vector describing the length and orientation of the mth edge of the plate,
is a vector describing the length and orientation of the mth edge of the plate, 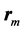 is the position vector of the midpoint of the th edge,
is the position vector of the midpoint of the th edge,  is the length of the projection of
is the length of the projection of 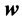 onto the plane of the plate,
onto the plane of the plate, 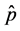
is






2.2. Effect on the Surface Property
Referring to Figure 1. Consider the PO solution for a multilayered facet. The interaction of an incident electromagnetic field with a non-perfectly conducting multilayered facet can be described by Fresnel’s reflection coef-
Figure 1. Geometry of multilayered facet.
ficients 



where 






rization, respectively. The Nth layer is assumed to be semi-infinite long, and the input impedances of the Nth layer is given by

The impedance of the nth layer is

2.3. Multi-Bounce Effect in Exterior and Interior Structure
For considering multi-bounce effect in exterior and interior structure, combination of GO and PO methods is used [9]. GO is used for finding reflected or transmitted paths. PO is applied at last bounce time. Effect area is obtained as shown in Figure 2. A path of transmitted wave into interior structure is calculated by using Snell’s law.
3. Numerical RCS Analysis
RCS computation is performed for a type of warship. Model which has a curvature is divided into many flat plates. RCS of each flat plate is evaluated using Equation (2).
A Type of Warship
A warship model for RCS calculation is shown in Figure 3. The overall length, width and draft of the warship are 000 m, 00 m and 0 m, respectively which are blind in the security classification. The mesh model is composed of 4675 nodes and 4065 elements as shown Figure 3.

Figure 2. Concept of multi-bounce: (a) multi-bounce paths and (b) effective area.
The range of the incident angle is 


At first, the RCS results of the contribution of the incident angle are shown in Figure 4.
The RCS results of the warship model with the elevation angle are shown in Figure 5.
The RCS of the warship model with electronic coating on its surfaces is then analyzed. Electronic coating is applied as shown in Figure 6.
The RCS results with electronic coatings are shown in Figure 7.
Figure 3. Analysis model and range.
Figure 4. The RCS results of the contribution of the incident angle.


Figure 5. RCS results with the elevation angle: (a)





Figure 6. Electronic coating applied on a warship surface: (a) case 1; (b) case 2.

Figure 7. RCS results with electronic coating applied: (a) case 1; (b) case 2.
4. Conclusion
To predict RCS of ship at design stage, RACSAN software is developed. This program is based on Kirchhoff approximation in PO as high frequency method. The RCS of ship model is numerically simulated by using this program. Various effects, which are multi-bounce effect in exterior and interior structure by combination of GO and PO methods, electronic coating effect by using reflection coefficient, and response time pattern for detected target are considered. It is expected that RCS of ship can be continuously managed by simulation when ship shape is changed at design stage and controlled by predicting electronic coating effects applied on specific parts by using this program.
Cite this paper
Joon-Tae Hwang,Suk-Yoon Hong,Jee-Hun Song,Hyun-Wung Kwon, (2015) Radar Cross Section Analysis Using Physical Optics and Its Applications to Marine Targets. Journal of Applied Mathematics and Physics,03,166-171. doi: 10.4236/jamp.2015.32026
References
- 1. Urick, R.J. (1983) Principles of Underwater Sound. 3rd Edition, McGraw-Hill, New York.
- 2. Okumura, T., Masuya, T., Takao, Y. and Sawada, K. (2003) Acoustic Scattering by an Arbitrarily Shaped Body: An Application of the Boundary-Element Method. ICES Journal of Marine Science, 60, 563-570. http://dx.doi.org/10.1016/S1054-3139(03)00060-2
- 3. Thompson, L.L. and Pinsky, P.M. (1996) A Space-Time Finite Element Method for the Exterior Acoustics Problems, Journal of the Acoustical Society of America, 99, 3297-3311. http://dx.doi.org/10.1121/1.414887
- 4. Klement, D., Preissner, J. and Stein, V. (1988) Special Problems in Applying the Physical Optics Method for Backscatter Computation of Complicated Objects. IEEE Transactions on Antennas and Propagation, 36, 228-237. http://dx.doi.org/10.1109/8.1100
- 5. Stanton, T.K. (2000) On Acoustic Scattering by a Shell-Covered Seafloors. Journal of the Acoustical Society of America, 108, 551-555. http://dx.doi.org/10.1121/1.429585
- 6. Ufimtsev, P.Y. (1991) Elementary Edge Waves and the Physical Theory of Diffraction. Electromagnetics, 11, 125-160. http://dx.doi.org/10.1080/02726349108908270
- 7. Keller, J.B. and Ahluwalia, D.S. (1971) Diffraction by a Curved Wire. SIAM Journal on Applied Mathematics, 20, 390-405. http://dx.doi.org/10.1137/0120043
- 8. Schneider, H.G., Berg, R., Gilroy, L., Karasalo, I., MacGillivray, I., Morshuizen, M.T. and Volker, A. (2003) Acoustic Scattering by a Submarine: Results from a Benchmark Target Strength Simulation Workshop. 10th International Congress on Sound and Vibration, Stockholm, 7-10 July 2003, 2475-2482.
- 9. Knott, E.F., Shaeffer, J.F. and Tuley, M.T. (1993) Radar Cross Section. 2nd Edition, Artech House, Inc., Boston. http://dx.doi.org/10.1137/0120043
- 10. Gordon, W.B. (1975) Far Field Approximation of the Kirchhoff-Helmholtz Representation of Scattered Field. IEEE Transactions on Antenna and Propagation, 23, 590-592. http://dx.doi.org/10.1109/TAP.1975.1141105
- 11. Kim, K. High-frequency Back-scattering Analysis and Its Application to Marine Targets. Pusan National Univ., Pusan.
- 12. Brekhovskikh, L.M. (1960) Waves in Layered Media. Academic Press, New York.
NOTES
*Corresponding author.














