Journal of Applied Mathematics and Physics
Vol.03 No.02(2015), Article ID:53667,5 pages
10.4236/jamp.2015.32025
Turbulent-Induced Noise around a Circular Cylinder Using Permeable FW-H Method
Woen-Sug Choi1*, Suk-Yoon Hong1, Jee-Hun Song2, Hyun-Wung Kwon3, Chul-Min Jung4, Tae-Gyoung Kim1
1Departmentof Naval Architecture and Ocean Engineering, Seoul National University, Seoul, Republic of Korea
2Department of Naval Architecture and Ocean Engineering, Chonnam National University, Yeosu, Republic of Korea
3Department of Naval Architecture and Ocean Engineering, Koje College, Koje, Republic of Korea
4Advanced Naval Technology Center, NSRDI, Agency for Defense Development, Chinhae, Republic of Korea
Email: *kickflipin@snu.ac.kr, syh@snu.ac.kr, taegyoung@snu.ac.kr, jhs@jnu.ac.kr, khw1@snu.ac.kr, cmjung@add.re.kr


Received 19 November 2014

ABSTRACT
Varieties of research on turbulent-induced noise are conducted with combinations of acoustic analogy methods and computational fluid dynamic methods to analyse efficiently and accurately. Application of FW-H acoustic analogy without turbulent noise is the most popular method due to its calculation cost. In this paper, turbulent-induced noise is predicted using RANS turbulence model and permeable FW-H method. For simplicity, noise from 2D cylinder is examined using three different methods: direct method of RANS, FW-H method without turbulent noise and permeable FW-H method which can take into account of turbulent-induced noise. Turbulent noise was well predicted using permeable FW-H method with same computational cost of original FW-H method. Also, ability of permeable FW-H method to predict highly accurate turbulent-induced noise by applying adequate permeable surface is presented. The procedure to predict turbulent- induced noise using permeable FW-H is established and its usability is shown.
Keywords:
Turbulent-Induced Noise, Circular Cylinder, Acoustic Analogy, FW-H Method, Permeable FW-H Method

1. Introduction
Objects in motion in fluid disturb its surroundings to produce noise. Such noise can be predicted using Kirchhoff formula or Acoustic analogy [1]. The Acoustic analogy method has advantage over Kirchhoff formula due to its representation of noise in three pressure terms according to its physical meanings: thickness noise, loading noise and quadruple noise [2]. Meanwhile, in the view point of far-field radiation noise, turbulent-induced quadrupole noise term has usually been neglected to reduce computational cost [1]. Moreover, it has recently been found that the turbulent-induced noise is also important to understand characteristics of overall noise in far-field [3].
The turbulent-induced noise can be predicted correctly using DNS (Direct Numerical Simulation) method. However it is almost impossible because of high computational cost [4] [5]. Therefore, hybrid method to utilize computational fluid dynamics (CFD) with turbulent models and acoustic analogy introduced by Lighthill to reduce computational expense is being researched actively [1]. Based on Lighthill’s analogy [6], FW-H (Ffowcs Williams and Hawkings) analogy [2] without considering quadrupole term is commonly used to consider object moving in arbitrary motion [7].
In this study, the use of RANS (Reynolds Averaged Navier-Stokes) turbulent model of CFD and permeable FW-H which accommodates permeable surface is shown to predict turbulent-induced noise. Direct method to directly extract perturbing pressure, FW-H method without quadruple term, and permeable FW-H which includes the effects of turbulence are compared for 2-dimensional circular cylinder. Permeable FW-H method has shown to well predict the influence of turbulent noise compared to the method without quadruple term. Moreover, it is shown that careful selection of permeable surface can result in high accuracy from permeable FW-H method.
2. Basic Theory of Acoustic Analogy
Lighthill has introduced the wave equation of acoustic analogy having the source derived by comparing the exact equations of motion of a fluid with the equations of sound propagation in a medium at rest as follows [6],
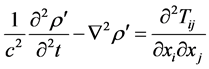 (1)
(1)
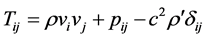 (2)
(2)
Here 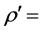 density perturbation,
density perturbation, 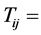 light hill’s stress tensor,
light hill’s stress tensor, 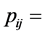 compressive stress tensor,
compressive stress tensor,  velocity of sound in fluid at rest,
velocity of sound in fluid at rest, 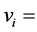 component of velocity in direction
component of velocity in direction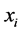 .
.
Curle’s analogy have expanded the Lighthill’s theory considering rigid surface (Curle, 1995), an Ffowcs Williams and Hawkings have further generalized the theory considering rigid object in arbitrary motion as follows [2],
 (3)
(3)
Here, 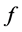 represents body surface as function of
represents body surface as function of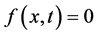 ;
; 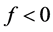 and
and 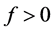 meaning inside and outside of rigid body, respectively. First term physically means unsteadiness inside the fluid expressed in quadruple source as Reynolds stress which is called turbulent-induced term. Second term is monopole source due to dilatation of boundaries and third term is dipole source modeled from fluctuating stresses on the surface. Second term and third term is called loading noise term and thickness noise terms, respectively.
meaning inside and outside of rigid body, respectively. First term physically means unsteadiness inside the fluid expressed in quadruple source as Reynolds stress which is called turbulent-induced term. Second term is monopole source due to dilatation of boundaries and third term is dipole source modeled from fluctuating stresses on the surface. Second term and third term is called loading noise term and thickness noise terms, respectively.
Farassat’s formulation develops FW-H analogy equation into following integral forms [8],
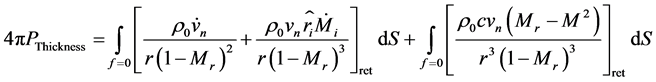 (4)
(4)
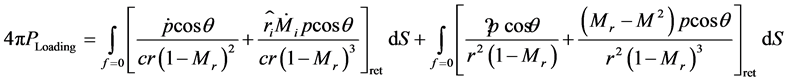 (5)
(5)
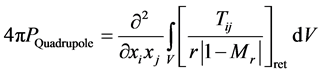 (6)
(6)
Here,  is Doppler factor,
is Doppler factor, 

Turbulent term which is represented as quadrupole source is in volume integration. Decision of the volumes in fluid around rigid body to integrate and evaluation of the integration kernel is difficult [9]. Permeable FW-H method starts from setting the permeable surface by modifyingthe assumption of surface 



3. Noise Analysis of 2-Dimensional Circular Cylinder
3.1. Construction of Mesh
To analyze the circular cylinder with 20 mm diameter, total of 218,268 cells are constructed. Receiver points for acoustic analysis are place at perpendicular to the flow direction downward from the cylinder in distance of 10 mm, 70 mm. Dimensionless Wall Distance (Wall Y+) is set to lower than 1 to accurately calculate boundary layers. In addition, overall mesh takes from of C-H for better quality such as skewness and orthogonality around the cylinder.
Permeable surface (Inner-Cell) for permeable FW-H method is set to include boundary layers and 3 - 4 vortex shedding as in Figure 1.
3.2. Simulation of Turbulent Flow
Ansys FLUENT v14.5 is used for CFD calculation and also FW-H method without turbulent term and permeable FW-H with Inner-Cell boundary condition [7]. CFD calculation is done in pressure based, transient 2nd-or- der implicit in time and 3rd-order MUSCL in space with SIMPLE scheme and results are shown in Figure 2. To verify the flow simulation, the results are compared with the reference [10].
Figure 2(a) and Figure 2(b) show flow simulation results of dynamic pressure and pressure coefficient. Figure 2(b) shows good agreement with the reference [11]. In Table 1, it is verified the Strouhal number of simulation compared to references [10] [11].
Figure 1. Structured mesh with permeable surface (Inner-Cell), 218,168 volume cells.
Figure 2. CFD results of the circular cylinder: left: dynamic pressure; right: pressure coefficient.
Table 1. Comparison of Strouhal number.
3.3. Turbulent-Induced Noise Analysis
Figure 3 shows results due to different methodology to predict turbulent-induced noise. Direct method to directly extract perturbing pressure, FW-H without quadruple term which means turbulent noise (FW-H w/0 Quad.) and Permeable FW-H method by using permeable surface (Inner-Cell) are compared. The difference between the FW-H w/o Quad. and Permeable FW-H can be considered as the noise due to the turbulence with the magnitude of 10 dB ref 20 μPa. The results shows good results except the results at receiver 1 which is inside the permeable surface.
Considering the fact that the FW-H without quadruple term cannot represent the noise by the turbulence implies that the permeable FW-H method has well predicted the turbulence-induced noise. It can be stated from the result that the procedure to predict turbulent-induced noise is established. Also, it is shown that the Permeable FW-H method is robust compared to the standard FW-H method.
3.4. Turbulent-Induced Noise Analysis Underwater
Figure 4 shows results by the same procedure but underwater environment. Considering the Reynolds number, the fluid velocity is set to be 10 m/s. Comparing to the results that of the air, the noise due to the turbulence shows the magnitude of 20 dB 10 μPa and also the quadruple noise reduces overall noise at the range over 200 Hz.
Here, permeable FW-H also shows good agreement toward the direct method showing the similar characteristics that of the results in air. This also represents the robustness of the permeable FW-H method.
Accurate results can be obtained from FW-H methods inside the permeable surface both in air and underwater. In Figure 5, it is shown that the results of the permeable FW-H method by using the reversed permeable surface well match the direct method inside the permeable surface. In conclusion, the choice of Inner-Cell has great influence in the final prediction of turbulence noise.
Figure 3. Comparison of sound pressure level spectrum obtained from different method at 30 m/s, Receiver 1 (10 mm), Receiver 4 (70 mm).
Figure 4. Comparison of sound pressure level spectrum underwater obtained from different method at 10 m/s, Receiver 1 (10 mm), Receiver 4 (70 mm).
Figure 5. Comparison of sound pressure level spectrum underwater having permeable FW-H method with reversed normal vector at 10 m/s, Receiver 1 (10 mm), Receiver 4 (70 mm).
4. Conclusions
Prediction of the turbulence-induced noise around 2-dimensional circular cylinder is done by the three different methods: direct method to directly extract perturbing pressure, FW-H without quadruple term which represents the noise due to the turbulence and permeable FW-H method which includes the turbulent-induced noise.
The difference between the direct method and the FW-H without quadruple term represents the magnitude of the noise due to the turbulence. Permeable FW-H method shows good agreement with the direct method. The robustness of the permeable FW-H method is shown from different results that the permeable FW-H method can well predict the noise produced from turbulence. By reversing the normal vector of the permeable surface, the near-field prediction could improve its accuracy. In conclusion, the procedure to predict turbulent-induced noise by using the permeable FW-H method is established and its usefulness is shown.
In further studies, the selection of Inner-Cell considering not only the size of the surface but also the length and frequency of vortex shedding and turbulent-induced noise prediction in more complex geometries are considered to generalize the current procedure of predicting the turbulent-induced noise.
Cite this paper
Woen-Sug Choi,Suk-Yoon Hong,Jee-Hun Song,Hyun-Wung Kwon,Chul-Min Jung,Tae-Gyoung Kim, (2015) Turbulent-Induced Noise around a Circular Cylinder Using Permeable FW-H Method. Journal of Applied Mathematics and Physics,03,161-165. doi: 10.4236/jamp.2015.32025
References
- 1. Wang, M., Freund, J.B. and Lele, S.K. (2006) Computational Prediction of Flow-Generated Sound. Annual Review of Fluid Mechanics, 38, 483-512. http://dx.doi.org/10.1146/annurev.fluid.38.050304.092036
- 2. Ffowcs Williams, J.E. and Hawkings, D.L. (1969) Sound Generation by Turbulence and Surfaces in Arbitrary Motion. Philosophical Transactions of the Royal Society of London A, 264, 321-342. http://dx.doi.org/10.1098/rsta.1969.0031
- 3. Ianiello, S., Muscari, R. and Di Mascio, A. (2014) Ship Underwater Noise Assessment by the Acoustic Analogy, Part II: Hydroacoustic Analysis of a Ship Scaled Model. Journal of Marine Science and Technology, 3, 52-74. http://dx.doi.org/10.1007/s00773-013-0236-z
- 4. Singer, B.A. and Lockard, D.P. (2003) Hybrid Acoustic Predictions. Computers and Mathematics with Applications, 46, 647-669. http://dx.doi.org/10.1016/S0898-1221(03)90023-X
- 5. Inoue, O. and Hatakeyama, N. (2002) Sound Generation by a Two-Dimensional Circular Cylinder in a Uniform Flow. Journal of Fluid Mechanics, 471, 285-314. http://dx.doi.org/10.1017/S0022112002002124
- 6. Lighthill, M.J. (1952) On Sound Generated Aerodynamically, I: General Theory. Proceedings of the Royal Society, A221, 564-587. http://dx.doi.org/10.1098/rspa.1952.0060
- 7. Ansys (2009) Ansys Fluent 12.0 “Theory Guide”, Ansys.
- 8. Frassat, F. (2007) Derivation of Formulations 1 and 1A of Farassat, NASA/TM-2007-214853.
- 9. Farassat, F. and Brentner, K.S. (1988) Supersonic Quadrupole Noise Theory for High-speed Helicopter Rotors. Journal of Sound and Vibration, 218, 481-500. http://dx.doi.org/10.1006/jsvi.1998.1836
- 10. Park, I.C. (2012) 2-Dimensional Simulation of Flow-Induced Noise around Circular Cylinder. Theses and Dissertations, Chungnam University.
- 11. Orselli, R.M., Meneghini, J.R. and Saltra, F. (2009) Two and Three-Dimensional Simulation of Sound Generated by Flow around a Circular Cylinder. American Institute of Aeronautics and Astronautics, AIAA 2009-3270.
NOTES
*Corresponding author.












