Journal of Applied Mathematics and Physics
Vol.03 No.02(2015), Article ID:53657,6 pages
10.4236/jamp.2015.32020
Scalar Particles’ Tunneling and Effect of Quantum Gravity
Guoping Li, Xiaotao Zu
School of Physical Electronics, University of Electronic Science and Technology of China, Chengdu, China
Email: li_gp2009@163.com


Received 17 November 2014

ABSTRACT
According to the generalized uncertainty principle (GUP), the Klein-Gordon equation is corrected by the quantum gravity exactly. Hence, the corrected Klein-Gordon equation will be more precise on the expression of the tunneling behavior. Then, the corrected Hawking temperature of the Gibbons-Maeda-Dilaton black hole is obtained near the horizon by quantum gravity. Analyzing the results carefully, it is obvious for us that the tunneling result is not only related to the mass of black hole, but also related to the mass and energy of outgoing fermions. Finally, we also infer that the tunneling radiation would be stopped at some particular temperature.
Keywords:
The Quantum Gravity, The Gibbons-Maeda-Dilaton Black Hole, The Corrected Klein-Gordon Equation, The Generalized Uncertainty Principle

1. Introduction
Hawking radiation can be regard as the tunneling process which the vacuum fluctuation caused at the event horizon of black holes [1] [2]. Then, more and more attentions of theoretical physicists are focused on the Hawking radiation. Since 1976, T Dmour and Sannan developed Hawking radiation greatly with the relativistic quantum mechanics and the quantum field theory. In this way, a lot of work had been done by Zhao et al. [3]. Later, a semi-classical quantum tunneling method was proposed to study the Hawking radiation of black holes by Parikh et al. [4] [5]. After that, the process of calculation on the Hawking temperature has been greatly simplified, and then many effects take into account. The centre of this method can be regard as two parts; one is the expression
of the wave function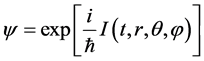 , and the other is the WKB approximation. Later, the dynamical
, and the other is the WKB approximation. Later, the dynamical
black hole, the de Sitter black hole and the higher dimensional black hole, have been studied by using this method, and some important similar results were obtained. In 2007, Kerner and Mann developed this method once more [6]. Then, the tunneling method can be applied to study the dynamics behavior of spin 1/2 particles, and the Hawking temperature of 1/2-spin particles was also obtained. After that, many effects work on it and important results are obtained [7]-[12]. Now, the quantum tunneling theory has been the one of most popular theories on the calculation of Hawking temperature in black holes.
Recently, the quantum gravity theory came into a period of rapid development. For example, the most important symbol is the appearance of the supergravity theory and loop quantum gravity theory. Obviously, the best application model of the quantum gravity is black hole model. More and more evidences imply that the generalized uncertainty principle (GUP) can be modified by the modified fundamental commutation relation; therefore the momentum operator will be corrected with it. Finally, the dynamics equation of particles in black holes can be modified by the quantum gravity, and the Hawking radiation is corrected. Also, many other various modifications can be found in [13]. Through the quantum tunneling method and the GUP, the tunneling behavior of the scalar particle of Schwarzschild black hole has been studied by K Nozari [14]. And many other studies of the tunneling behavior have been discussed in [15]-[18]. Lots of evidences indicate that the quantum gravity research has the important correction on the Hawking radiation.
The aim of this paper is to study the tunneling radiation of scalar particles in the Gibbons-Maeda-Dilaton black hole with the Klein-Gordon equation near the horizon. With the careful calculation, the corrected tunneling rate and corrected Hawking temperature are obtained. The rest paper proceeds as follows: Section 2 introduces the modified Klein-Gordon equation; Section 3 studies the Hawking radiation of scalar particles in the Gibbons-Maeda-Dilaton black hole with the Klein-Gordon equation; Section 4 calculates the residuum of black hole; Section 5 is only a conclusion.
2. The Corrected Klein-Gordon Equation
In this section, we will discuss the modified Klein-Gordon equation by the quantum gravity. More and more evidences indicate that the generalized uncertainty principle (GUP) can describe the minimum measurable length [19]-[23]. Based on the modified fundamental commutation relation [13]
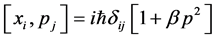 (1)
(1)
The expression of GUP can be express as [17]
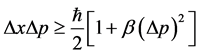 (2)
(2)
where, 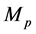 is the Planck mass,
is the Planck mass, 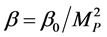 ,
, 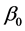 is a dimensionless parameter and
is a dimensionless parameter and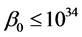 ,
, 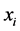 and
and 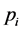 can be found in the reference [17],
can be found in the reference [17],
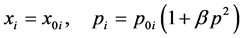 (3)
(3)
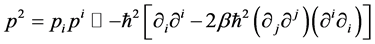 (4)
(4)
The canonical commutation relations express as 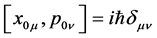 should be satisfied. The Klein-Gordon
should be satisfied. The Klein-Gordon
equation without the electromagnetic field is given by the following form [24],
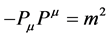 (5)
(5)
To studied the effect which the quantum gravity have on the Klein-Gordon equation, we expand the Klein- Gordon equation as two parts, so we rewrite this equation as,
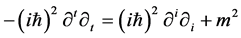 (6)
(6)
In above equation, the left hand is related to the square of energy, and the right hand is related to the square of coordinate. In reference [17], considering the mass-energy shell condition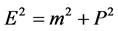 , the generalized expression of energy is,
, the generalized expression of energy is,
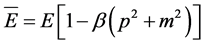 (7)
(7)
Therefore, after we substituted Equations (3), (4) and (7) into Klein-Gordon equation, the modified Klein- Gordon equation are given as [24],
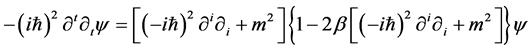 (8)
(8)
The modified Klein-Gordon equation tells us that the quantum gravity has an important influence on the dynamic equation of scalar particles. In the following section, we will focus on the tunneling behavior of scalar particles of the Gibbons-Maeda-Dilaton black hole with the corrected Klein-Gordon equation.
3. The Tunneling Radiation of the Gibbons-Maeda-Dilaton Black Hole
In this section, we are devoted to study tunneling radiation of scalar particles of the Gibbons-Maeda-Dilaton black hole by using modified Klein-Gordon equation. In 1991, Garfinkle D. et al. obtained the Gibbons-Maeda- Dilaton black hole solution, and the metric is,
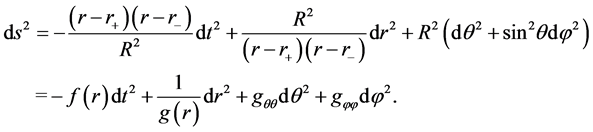
where, 
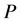
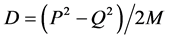
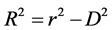
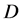
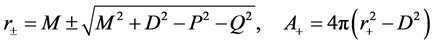
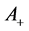
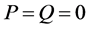
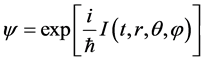
where 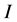

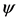

The equation of motion of scalar particles is obtained,

In above equation, the higher order terms of 
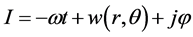
Here, 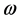
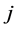
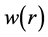
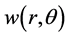
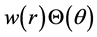
For the convenience, we fix the angle 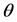
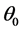
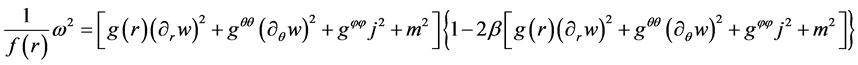
Therefore, the Equation (15) can be simplified as,

where,

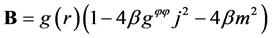
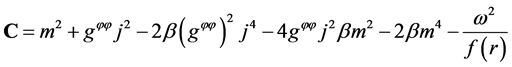
Then, we considered the condition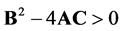
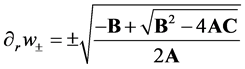
After we substituted Equations (9) and (10) into Equation (20), so the solution of this quartic equation at the horizon is,
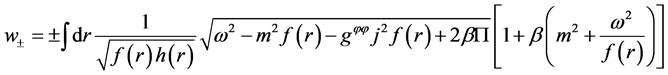
Here,
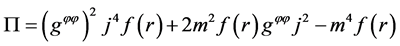
With the path integral, substituting the metric of the Gibbons-Maeda-Dilaton black hole into the above equation, the value 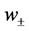
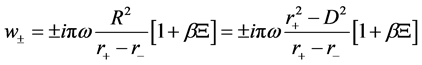
And, 

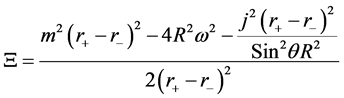
In this paper, the relation between the tunneling rate and action can be written as,
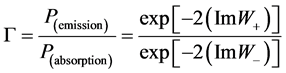
So the corrected tunneling rate of the Gibbons-Maeda-Dilaton black hole near the event horizon can be express as,
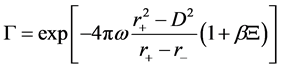
Therefore, the corrected Hawking temperature is,
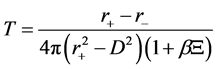
The corrected Hawking temperature of the Gibbons-Maeda-Dilaton black hole near the horizon can be rewritten as,
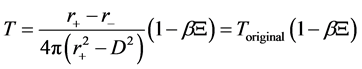
where, the 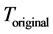
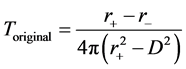
The expression of Equations (26)-(29) is the corrected Hawking temperature and corrected tunneling rate of Gibbons-Maeda-Dilaton black hole. Carefully analysis on the Equations (26)-(29), we can find that the corrected Hawking temperature is not related to the mass of the black hole, but related to the mass and energy of the outgoing particles. And this is due to the influence of quantum gravity, the Hawking radiation of the Gibbons- Maeda-Dilaton black hole are corrected. Further studies on the tunneling results, we can get the conclusion that the quantum correction slows down the increase of temperature during the tunneling radiation, and the tunneling radiation will be stopped at some particular temperature.
4. Residuum of the Gibbons-Maeda-Dilaton Black Hole
In [24], Wang has obtained the residuum of Schwarzschild black holes. Considering the massless particle, the Hawking temperature stops increasing when,

The residue mass and the upper limit value of temperature in black hole can be express as,
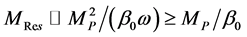
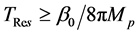
Here, 
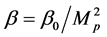
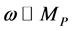
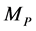
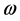
Equation (31) is the expression of the residuum of the Gibbons-Maeda-Dilaton black hole. In the calculation of Equation (31), the condition which 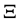
5. Conclusions
In this letter, we investigated the quantum tunneling radiation of scalar particles of the Gibbons-Maeda-Dilaton black hole. The results indicate that the tunneling radiation is not only related to the mass of the Gibbons-Maeda- Dilaton black hole, but also related to the mass and energy of the outgoing particle. So we can realize that the Hawking radiation is effected by the quantum gravity. In Equation (31), the parameters 
be obtained which is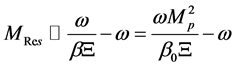
In a conclusion, the quantum gravity has attracted more and more attention of physicists. In this paper, we only calculated the tunneling behavior of scalar particles with effect of the quantum gravity. In future, we will focus on the other fields of the quantum gravity.
Acknowledgements
This work was supported by the National Foundation of China under Grant NO. 11178018.
Cite this paper
Guoping Li,Xiaotao Zu, (2015) Scalar Particles’ Tunneling and Effect of Quantum Gravity. Journal of Applied Mathematics and Physics,03,134-139. doi: 10.4236/jamp.2015.32020
References
- 1. Hawking, S.W. (1974) Black Hole Explosions. Nature, 30, 248.
- 2. Hawking, S.W. (1975) Particle Creation by Black Hole. Commun Math Phys., 43, 199. http://dx.doi.org/10.1007/BF02345020
- 3. Zhao, Z. (1992) A Universal Method Determining Hawking Effect in Sherically Symmetric or Plane-Symmetric Non- Static Space-Times. Chin Phys Lett, 9, 401.
- 4. Kraus, P. and Wilczek, F. (1995) Self-Interaction Correction to Black Hole Radiance. Nucl Phys B, 433. arXiv: 9408003[gr-qc]
- 5. Kraus, P. and Wilczek, F. (2000) Hawking Radiation as Tunnelling. Phys Rev Lett, 85, 5042. http://dx.doi.org/10.1103/PhysRevLett.85.5042
- 6. Kerner, R. and Mann, R.B. (2008) Charged Fermions Tunnelling from Kerr Newman Black Holes. Phys Lett B, 665, 277-283. http://dx.doi.org/10.1016/j.physletb.2008.06.012
- 7. Li, G.P., Zhou, Y.G. and Zu, X.T. (2013) Particles Tunneling of the Spherically Symmetric Black Hole with Dark Matter. Int J Theo.Phy, 52, 4025.
- 8. Chen, D.Y. and Yang, S.Z. (2007) Hamilton-Jacobi Ansatz to Study the Hawking Radiation of Kerr-Newman-Kasuya Black Holes. Int J Mod Phys A, 22, 5173. http://dx.doi.org/10.1142/S0217751X07038207
- 9. Lin, K. and Yang, S.Z. (2009) Fermion Tunneling from Higher-Dimensional Black Holes. Phys Rev D, 79, Article ID: 064035. http://dx.doi.org/10.1103/PhysRevD.79.064035
- 10. Chen, D. and Yang, S.Z. (2007) Hawking Radiation of the Vaidya Bonner de Sitter Black Hole. New J Physi, 9, 252. http://dx.doi.org/10.1088/1367-2630/9/8/252
- 11. Jiang, Q.Q. (2008) Dirac Particle Tunneling from Black Rings. Phys Rev D, 78, Article ID: 044009. http://dx.doi.org/10.1103/PhysRevD.78.044009
- 12. Chen, D.Y. and Yang, S.Z. (2007) Charged Particle Tunnels from the Stationary and Non-Stationary Kerr-Newman Black Holes. Gen Relat Grav, 39, 1503. http://dx.doi.org/10.1007/s10714-007-0478-3
- 13. Kempf, A., Mangano, G. and Mann, R.B. (1995) Hilbert Space Re-presentation of the Minimal Length Uncertainty Relation. Phys Rev D, 52, 1108. arXiv:9412167[hep-th]
- 14. Nozari, K and Saghafi, S. (2012) Parikh-Wilczek Tunneling from Noncommutative Higher Di-Mensional Black Holes. JHEP, 11, 005. arXiv:1206.5621[hep-th]
- 15. Chen, D.Y., Wu, H.W. and Yang, H.T. (2014) Observing Remnants by Fermions' Tunneling. JCAP, 3, 036.
- 16. Chen, D.Y. (2014) Dirac Particles’ Tunnelling from 5-Dimensional Rotating Black Strings Influenced by the Generalized Uncertainty Principle. EPJC, 74, 2687. http://dx.doi.org/10.1140/epjc/s10052-013-2687-0
- 17. Chen, D.Y., Jiang, Q.Q., Wang, P. and Yang, H.T. (2013) Remnants, Fermions’ Tunnelling and Effects of Quantum Gravity. JHEP, 1311, 176. http://dx.doi.org/10.1007/JHEP11(2013)176
- 18. Chen, D.Y. and Li, Z.H. (2014) Remarks on Remnants by Fermions’ Tunnelling from Black Strings. Adv. High Energy Phys. arXiv:1404.6375
- 19. Townsend, P.K. (1977) Small-Scale Structure of Spacetime as the Origin of the Gravitational Constant. Phys Rev D, 15, 2795. http://dx.doi.org/10.1103/PhysRevD.15.2795
- 20. Amati, D., Ciafaloni, M. and Veneziano, G. (1989) Can Spacetime Be Probed below the String Size? Phys Lett B, 216, 41. http://dx.doi.org/10.1016/0370-2693(89)91366-X
- 21. Konishi, K., Paffuti, G. and Provero, P. (1990) Minimum Physical Length and the Generalized Uncer-Tainty Principle in String Theory. Phys Lett B, 234, 276. http://dx.doi.org/10.1016/0370-2693(90)91927-4
- 22. Garay, L.J. (1995) Quantum Gravity and Minimum Length. Int J Mod Phys A., 10, 145. [arXiv:9403008[gr-qc]
- 23. Amelino-Camelia, G. (2002) Relativity in Space-Times with Short-Distance Structure Governed by an Observer-Independent (Planckian) Length Scale. Int J Mod Phys D, 11, .35. arXiv:0012051[gr-qc]
- 24. Wang, P., Yang, H.T. and Ying, S.X. (2014) Quantum Gravity Corrections to the Tunneling Radiation of Scalar Particles. arXiv:1410.5065[gr-qc]

