Received 15 October 2014

ABSTRACT

A two-body regularization for N-body problem based on perturbation theory for Keplerian problem is discussed. We provide analytical estimations of accuracy and conduct N-body experiments in order to compare it with state-of-the-art Hermite integrator. It is shown that this regularization keeps some features that allow overcoming KS-regularization in some particular cases.

Keywords:

N-Body Problem, Numerical Simulations

1. Introduction

The N-body problem appears to be one of the most famous unsolved problems of mathematical physics. The area of its applications is tremendously wide, from simulations of DNA and ferrofluids [1] to star clusters, galaxies and large-scale structure of the universe [2]. In case of self-gravitating system, it can be solved analytically just for two and three [3] bodies. This leads to the necessity of the numerical approach, which has been developing for more than 50 years. The recent state of the gravitational N-body simulations is presented in various review articles, e.g. [2].

In order to simulate many-body systems with a required level of precision, the corresponding algorithm should be selected. For so-called collisional [4] self-gravitating systems like globular clusters and galactic cores one has to apply direct summation method with complexity of 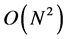which allows reaching the mean value of relative error up to, corresponding to the finite bit precision error [5]. The recent achievement of the collisional N-body codes is the direct simulation of 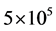particles on the Hubble time [2]. Further growth of

this number seems to be of little avail for 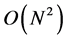algorithm. A new method of FMM implementation in colli-

sional code [5] is said to be scaled with time as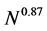; however, it is not state-of-the-art approach at the moment. To sum up, the field of collisional N-body simulations is yet to be developed in order to simulate existing physical systems.

One of the classical difficulties of the collisional N-body problem is the regularization of equations of motion. It is clear that the accelerations of two particles approach infinity when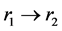. Numerical integration of such singularities faces some obstacles and gives a rise to numerical errors. Reaching the relative error of finite bit precision demands either decreasing the integration timestep or the transformation to another coordinates in which the equations have no singularity [6] [7]. The current paper describes the final adjusting of a regularization method based on perturbation theory for Keplerian problem [8]. An idea of this method cannot be considered as absolutely new one. From the physical point of view, it’s natural to make the transformation to action-angle variables and to treat external forces acting on the binary star as a small disturbance. However, this kind of regularization, despite its understandable physical origin, is not discussed in review articles. The reason for that is that its accurate implementation demands a number of numerical tricks that are not simple to formalize. At the moment of the writing this article, after three years of the numerical experiments and method development, we can state with a confidence that this seeming to be physical method raises a number of obstacles that are not as easy to catch and overcome. However, from the analytical point of view, perturbation-based method has its own field of the use, at least, numerical simulation of “hard binaries” in a weak external gravitational field in the framework of collisional N-body code. Below we try to show the cases that should be calculated with this method rather than KS-regularization.

The Hamiltonian of the gravitational N-body problem is written in the form of:

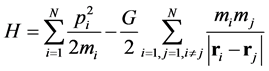(1)

This Hamiltonian leads to the equations of motion:

(2)

where 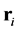is the radius vector of the ith body and is the vector drawn from the ith body to the jth body. At fixed initial coordinates and velocities of all bodies, the problem is reduced to the Cauchy problem and has a unique solution. Thus, solving the N-body problem is reduced to numerically solve a system of differential equations with fixed initial conditions.

2. Current Approach

The approach based on the perturbation theory for the Keplerian problem previously was discussed in [8]. Let us recall its main issues. The Hamiltonian of our system is written by (1). Below, we will consider the specific p-th body and assume that the body nearest to it has number. Let us separate out the part of the Hamiltonian containing the singularity and call it: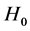

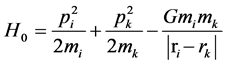(3)

From the view point of analytical mechanics, the solution of the Keplerian problem looks simplest in action variables. Let us now assume that the pair formed by the kth and pth bodies is sufficiently close (the tidal forces from the interaction with other bodies are much weaker than the interaction force between the two chosen bodies). The exact trajectories of these two bodies can then be considered as an unperturbed motion, while we will take into account the influence of the surrounding bodies as a small correction. In this case, the integration step will be determined by the perturbation 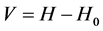and can be chosen to be considerably larger than in the standard technique of series expansion and application of Aarseth formula for calculating the step. Indeed, the classical two-body KS-regularization allows to avoid singularity by the coordinate transformation and leads to the equation like

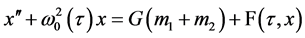(11)

As we consider 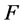as an action of the other bodies, we cannot make it analytically, so we have to integrate it numerically. The point is to choose the relevant integration timestep. Let us imagine that the RHS can be expanded in Fourier series as

.

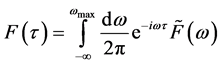In order to resolve the trajectory with the fixed level of accuracy, we have to choose timestep, for example, from the formula

where denotes to the resolution of the trajectory. The limit of gives us that we cannot choose the timestep lower than in order to resolve binary star system. Opposite to KS, the regularization described

below allows to set up the integration timestep up to infinity [7]. The criteria of regularization can be written in the following form:

(12)

which means that if the normal timestep chosen from Aarseth formula (see [2]) is much smaller than -timestep for the system with turning off the nearest body, then we should apply our regularization technique. Actually, this criteria gives the condition of applicability of perturbation theory (like) in most cases. If we consider three body problem and write down the explicit relations for acceleration and jerk

values and substitute them in criteria (12), we get the condition, where these values correspond to

two others body, and if we assume their velocities to be of the same order of magnitude, we could get that, from which we immediately get the condition of applicability of perturbation theory.

In development of presented method some improvements were made. First of all, calculation of the jerk and snap (first and second time derivatives of acceleration) of each body are corrected to the time in which we integrate bodies in the current iteration. Besides, prediction of the position, velocity and acceleration of the bodies which are integrated by straight scheme are performed by straight scheme, and the prediction of these parameters for regularized scheme are done with itself. So, the accuracy of method was increased using these predictor- like operations without any additional complexity.

Some further corrections were made with integration timestep calculation. Using only straight scheme of integration without regularization, it is simple to estimate the third derivative of acceleration by dividing snap difference for the end and the beginning of the step by its duration. But the regularized procedure doesn’t allow estimating the third derivative for acceleration in such a simple way, because time step is much larger. So the Aarseth semiempiric formula for time step is difficult to use straightly, as it uses the third acceleration derivative. To simplify our formula and to avoid zeroes in denominator, the following procedure was suggested. Let us

suppose that orders of values of derivatives decrease proportionally to their order, i.e. and. From these relations a set of approximation formulas for the third acceleration derivative can be obtained, for example. Substituting this expression to Aarseth formula finally This

approximation doesn’t use the third acceleration derivative and the denominator consists of 2 composes not proportional to each other as in Aarseth formula. The numeric testing has shown the effectiveness of such time step approximation.

As it was mentioned above the suggested method uses individual integration timestep for each body, but it was not discussed in detail in [8]. However, this procedure is worthy to be described in more detail, because it has important influence on speed of integration and its precision. Let us take following designations: individual current time for body with number, , its current integration time step. So let’s consider the concrete step for body with number. At the beginning of the procedure this body possesses individual time and other bodies has their times and previous step times, So that the current time if the body with number is between the beginnings and the ends of time steps of the rest bodies, To calculate acceleration, jerk and snap of the body number it is necessary to calculate positions, velocities and accelerations of other bodies at time. It is possible to do with necessary precision because lies inside time steps of other bodies. So it is necessary to make a short virtual step for each body excluding for time from position corresponding time, In the case of step of i-body integration the corresponding procedure is used i.e. straight procedure is used for virtual step when such used for real step and procedure with regularization is used for virtual step, when it is used for real. Such procedure allows taking into consideration all differentials of the fourth order, while without it algorithm has only second order precision.

3. Numerical Experiment

In order to check the level of precision that can be achieved by the code described above, we conduct series of N-body experiments and compare the state-of-the-art Hermite code with our version. The algorithm of the verification is the following―we generate an initial snapshot with coordinates and velocities taken randomly in some range. All particles have masses equal to one solar mass. Using these initial conditions, we start a simulation within framework of regularized code and integrate only one timestep. The output of this calculation in which we are interested in are the new acceleration values of one or two bodies moved by one step of the algorithm. The same input is used for Hermite code, so we start the simulation and carry it up to the time that we have integrated by the regularized code. After these actions, we can compare calculated accelerations, considering the Hermite code output as the true solution of the N-body problem. There is a number of ways to compare two codes that have been discussed in [5]. We use the most trivial, plotting the distribution of errors normalized by acceleration calculated by Hermite integrator. This value is said to give the upper boundary to the real relative error, so our error estimations are somehow overstated. The Figure 1 represents this distribution:

The average error is on a level of, which is in a good agreement with criteria for the collisional code [5].

Another useful experiment is carried out to distinguish the reduction of the timestep for the ordinary algorithm from the precision level that is allowed by two-body regularization. As is said above, we formulate the criteria to choose the integration either by Taylor expansion or with the use of the regularization. If we increase the parameter, the possibility of the regularization to be turned on decreases incredibly, so in this limit we have the code with two layers of Ahmad-Cohen only. Comparison between this code and Hermite gives the average error of unregularized code is bigger than one achieved with regularization at least by the order of magnitude.

We also have conducted a numerical experiment analogous to one described in [8] in order to check the precision of integrals conservation. The simulation on relazation timescale gives the relative error up to, which should be considered as a good result for nonsymplectic and nonsymmetric integration scheme. The deviations of momentum of the system also appear to be small compared with its RMS value. The snapshots of this simulation are presented on the Figure 2 and Figure 3. Red and purple mark the bodies from different clusters; turquoise marks bodies that are intergated with the use of regularization procedure.

4. Discussion

We have discussed the final adjustments of the algorithm presented in [8]. At the moment, it allows conserving energy with the relative level of precision about. The average error is in agreement with criteria for collisional code [5]. The further development of collisional N-body algorithm demands some schemes for efficient and accurate calculation of the far-field impact. The Ahmad-Cohen scheme for 100 nearest bodies, regularization [8] and individual timestep choice are combined within the framework of the original N-body code. However, it still has complexity, which is unacceptable for the galactic core and globular cluster simulation. In the article [5], the fast multipole method is considered as the method for collisional modelling that allows decreasing the complexity at least to the level of. Realization of this kind of algorithm alongside with regularization described above seems to be perspective instrument for collisional N-body modelling.

Cite this paper

Sergey Chernyagin,Kirill Lezhnin, (2015) On the Semianalytical Two-Body Regularization in N-Body Simulations. Journal of Applied Mathematics and Physics,03,124-129. doi: 10.4236/jamp.2015.32018

References