Journal of Applied Mathematics and Physics
Vol.03 No.02(2015), Article ID:53651,8 pages
10.4236/jamp.2015.32015
Analysis of Nonlinear Dust-Acoustic Shock Waves in an Unmagnetized Dusty Plasma with q-Nonextensive Electrons Where Dust Is Arbitrarily Charged Fluid
G. Mandal*, N. Y. Tanisha
Department of Electronics and Communication Engineering, East West University, Dhaka, Bangladesh
Email: *gdmandal@ewubd.edu


Received 23 August 2014

ABSTRACT
The nonlinear propagation of dust-acoustic (DA) shock waves in three-component unmagnetized dusty plasma consisting of nonextensive electrons, Maxwellian ions and arbitrarily charged mobile dust grain has been investigated. It is found that the presence of q-nonextensive electrons and ions can change the nonlinear behavior of shock wave. The standard reductive perturbation method is employed to study the basic features (phase speed, amplitude and width) of DA shock waves (DASWs) which are significantly modified by the presence of Maxwellian ions and nonextensive electrons. The present investigation can be very effective for understanding the nonlinear characteristics of the DASWs in space and laboratory dusty plasmas.
Keywords:
Dusty Plasma, Nonextensive Electrons, Shock Waves, Solitary Waves

1. Introduction
The wave propagation in dusty plasmas has received much attention in the recent years because of its vital role in understanding different types of collective processes in space plasma environments, namely, lower and upper mesossphere, cometary tails, planetary rings, planetary magnetosphere, interplanetary spaces, interstellar media, etc. [1] [2]. The presence of charged dust grains in a plasma modifies the existing plasma wave spectra as well as introduces a number of novel eigen modes [viz. dust-ion acoustic (DIA) waves [3], dust-acoustic (DA) waves [4], dust lattice waves, etc.]. The dust grains acquire a negative charge by the collection of electrons [5] [6] because the thermal speed of the electrons is much higher than that of the ions. On the other hand, dust grains may become positively charged also due to a variety of processes including photo-electron emission by UV photons, thermoionic emission induced by radiative heating [5] [7], secondary electron production, etc. However, Shahmansouri and Tribeche have considered [8] the effects of arbitrary amplitude DA solitary waves in an unmagnetized, collisionless dusty plasma with electrons and ions featuring Tsallis distribution. Thus, arbitrarily (negatively or positively) charged dust is found to exist in most space and a laboratory dusty plasma system [5].
Over the last few decades, a great deal of attention has been paid to a nonextensive generalization of the Boltzmann-Gibbs-Shannon (BGS) entropy, first proposed by Tsallis [9]. The effects of nonextensivity of plasma constituents are quite common in astrophysical and cosmological scenarios like stellar polytropes [10], hadronic matter and quark-gluon plasma [11], protoneutron stars [12], collisionless thermal plasma [13] [14], etc. as well as its laboratory applications in nanomaterials, microdevices, and microstructures, etc. The nonextensive behavior of electrons and ions [13] (characterized by a parameter q) has been successfully employed in plasma physics. It is important to note that in case of 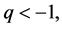 the q-distribution is not normalizable [2]. The strength of nonextensivity,
the q-distribution is not normalizable [2]. The strength of nonextensivity,  varies as
varies as 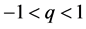 [2]. Furthermore, for
[2]. Furthermore, for 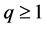 [2] [15], the distribution function exhibits Maxwell-Boltzmann velocity distribution. On the other hand, negative ions are found to be an extra component (which may occur naturally or may be injected form external sources) in most space [16] or laboratory dusty plasmas [3]. The presence of those negative ions significantly modifies the characteristic features of the nonlinear propagation of waves in a dusty plasma system [17] [18].
[2] [15], the distribution function exhibits Maxwell-Boltzmann velocity distribution. On the other hand, negative ions are found to be an extra component (which may occur naturally or may be injected form external sources) in most space [16] or laboratory dusty plasmas [3]. The presence of those negative ions significantly modifies the characteristic features of the nonlinear propagation of waves in a dusty plasma system [17] [18].
Recently, Shahmansouri and Tribeche [19] have studied the DA shock waves in a charged varying dusty plasma with nonextensive ions as well as electrons. Therefore, in this paper, we have presented a more generalized theoretical investigation on the properties of DA shock waves (DASWs) in a multi-species dusty plasma system consisting of arbitrarily charged cold mobile dust fluid, positively charged ions following Maxwellian distributions, and nonextensive electrons. We are particularly interested to observe the effect of number density, nonextensive electrons, and dust kinematic viscosity on the DASWs in the dusty plasma system under consideration. We have shown here that the variations of relative ion number densities and temperature-ratio (with respect to electrons) are the sources of dissipation and are responsible for the formation of DASWs.
The manuscript is organized as follows. The governing equations are provided in Section 2. The Burgers equation is derived in Section 3. The numerical solution of Burgers equation is presented in Section 4. Finally, a brief discussion is given in Section 5.
2. Governing Equations
We consider the nonlinear propagation of the DA waves in an unmagnetized dusty plasma system consisting of arbitrarily charged mobile dust, nonextensive distributed electrons, and Maxwellian distributed ions. Thus, at equilibrium we have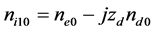 , where
, where 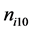 is the density of ions at equilibrium,
is the density of ions at equilibrium,  is the number of electrons residing onto the dust grain surface,
is the number of electrons residing onto the dust grain surface, 
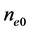 is the density of the electrons (dust particles) at equilibrium, and
is the density of the electrons (dust particles) at equilibrium, and  (+ for positively and-for negatively charged dust). The nonlinear dynamics of these low- frequency electrostatic DA waves in such a dusty plasma system, whose phase speed is much smaller than the electron and ion thermal speeds but greater than the dust thermal speed, is governed by
(+ for positively and-for negatively charged dust). The nonlinear dynamics of these low- frequency electrostatic DA waves in such a dusty plasma system, whose phase speed is much smaller than the electron and ion thermal speeds but greater than the dust thermal speed, is governed by
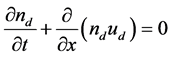 (1)
(1)
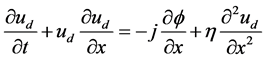 (2)
(2)
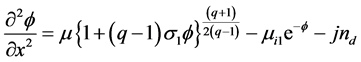 (3)
(3)
where 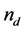 is the dust particle number density normalized by its equilibrium value
is the dust particle number density normalized by its equilibrium value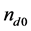 ,
, 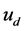 is the dust fluid speed normalized by
is the dust fluid speed normalized by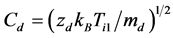 ,
, 









the magnitude of the electron charge. The time variable t is normalized by 


lian ions 


3. Derivation of Burgers Equation
To derive the Burgers equation (BE), we introduce the stretched coordinates [20] [21] as


where 









and develop equations in various powers of




Equation (13) describes the phase speed of DA waves regarding the dusty plasma under consideration. To the next higher order of



Now combining Equations (14)-(16), we obtain an equation of the form:

where


Equation (17) is known as Burger’s equation. The stationary localized solution of the BE is given by

where


4. Numerical Analysis
It is obvious from Equation (20), for




















5. Discussion
We have studied that the nonlinear propagation of DASWs in an unmagnetized dusty plasma consisting of arbitrarily charged mobile dust fluid, positive ions following Maxwellian distributions, and electrons following q- distribution. The propagation of the small amplitude nonlinear DASWs in dusty plasmas has been considered for analyzing the solution of the Burgers’ equation. The Burgers’ equation has been derived by using the reductive perturbation technique. The basic properties (i.e. polarity, amplitude, width, etc.) of the DASWs in dusty plasmas are found to be significantly modified by the number densities of ions (viz.


1. The dusty plasmas under consideration support finite-amplitude shock structures whose basic features (polarity, amplitude, width, speed, etc.) strongly depend on different plasma parameters, particularly, 

2. The widths of the DASWs in dusty plasmas with positively charged dust increase with increasing 

Figure 1. Showing the variation of width 





3. For positively charged dust



4. For



5. The effects of nonextensive parameter 


Figure 2. Positive shock structure is shown with the variation of 




Figure 3. Negative shock structure is shown with the variation of 




Figure 4. The variation of amplitude 






Figure 5. The variation of amplitude 






Figure 6. The variation of the solution 







Figure 7. The variation of the solution 







It can be noted here that the effects of the external magnetic field, nonplanar solitary [5] and shock structures, and their instabilities [3] are also problems of great importance, but are beyond the scope of our present investigation. Further, we stress that our present investigation should be very useful and effective in understanding the salient features of localized DASWs in space plasmas [3] [17].
Cite this paper
G. Mandal,N. Y. Tanisha, (2015) Analysis of Nonlinear Dust-Acoustic Shock Waves in an Unmagnetized Dusty Plasma with q-Nonextensive Electrons Where Dust Is Arbitrarily Charged Fluid. Journal of Applied Mathematics and Physics,03,103-110. doi: 10.4236/jamp.2015.32015
References
- 1. Mendis, D.A. and Rosenberg, M. (1994) Annu. Rev Astron. Astrophys., 32, 419. http://dx.doi.org/10.1146/annurev.aa.32.090194.002223
- 2. Verheest, F. (2000) Waves in Dusty Space Plasmas. Kluwer Academic Press, Dordrecht. http://dx.doi.org/10.1007/978-94-010-9945-5
- 3. Rosenberg, M. and Merlino, R.L. (2007) Planet Space Sci., 55, 1464. http://dx.doi.org/10.1016/j.pss.2007.04.012
- 4. Rao, N.N., Shukla, P.K. and Yu, M.Y. (1990) Planet. Space Sci., 38, 543. http://dx.doi.org/10.1016/0032-0633(90)90147-I
- 5. Shukla, P.K. and Mamun, A.A. (2002) Introduction to Dusty Plasma Physics. Institute of Physics Publishing Ltd., Bristol. http://dx.doi.org/10.1887/075030653X
- 6. Rosenberg, M. and Mendis, D.A. (1995) IEEE Trans. Plasma Sci., 23, 177. http://dx.doi.org/10.1109/27.376584
- 7. Goertz, C.K. (1989) Rev. Geophys., 27, 271. http://dx.doi.org/10.1029/RG027i002p00271
- 8. Shahmansouri, M. and Tribeche, M. (2013) Astrophys. Space Sci., 344, 99-104. http://dx.doi.org/10.1007/s10509-012-1296-y
- 9. Tsallis, C. (1988) J. Stat. Phys., 52, 479. http://dx.doi.org/10.1007/BF01016429
- 10. Plastino, A.R. and Plastino, A. (1993) Phys. Lett. A, 174, 384. http://dx.doi.org/10.1016/0375-9601(93)90195-6
- 11. Gervino, G., Lavagno, A. and Pigato, D. (2012) Central Euro. J. Phys., 10, 594. http://dx.doi.org/10.2478/s11534-011-0123-3
- 12. Lavagno, A. and Pigato, D. (2011) Euro. Phys. J. A, 47, 52. http://dx.doi.org/10.1140/epja/i2011-11052-1
- 13. Lima, J.A.S., Silva, R. and Santos, J. (2000) Phys. Rev. E, 61, 3260. http://dx.doi.org/10.1103/PhysRevE.61.3260
- 14. Pakzad, H.R. (2011) Phys. Scr., 83, Article ID: 015505.
- 15. Tribeche, M. and Merriche, A. (2011) Phys. Plasmas, 18, Article ID: 034502.
- 16. D’Angelo, N. (2004) J. Phys. D, 37, 860. http://dx.doi.org/10.1088/0022-3727/37/6/009
- 17. Mamun, A.A., Shukla, P.K. and Eliasson, B. (2009) Phys. Plasmas, 16, Article ID: 1145031. http://dx.doi.org/10.1063/1.3261840
- 18. Paul, A., Mandal, G., Mamun, A.A. and Amin, M.R. (2011) IEEE Trans. Plasma Sci., 39, 1254. http://dx.doi.org/10.1109/TPS.2011.2120627
- 19. Shahmansouri, M. and Tribeche, M. (2013) Astrophys. Space Sci., 346, 165-170. http://dx.doi.org/10.1007/s10509-013-1430-5
- 20. Schamel, H. (1972) J. Plasma Phys., 14, 905. http://dx.doi.org/10.1088/0032-1028/14/10/002
- 21. Schamel, H. (1973) J. Plasma Phys., 9, 377. http://dx.doi.org/10.1017/S002237780000756X
NOTES
*Corresponding author.









