Journal of Applied Mathematics and Physics
Vol.03 No.01(2015), Article ID:53601,5 pages
10.4236/jamp.2015.31014
Volatility Forecasting and Volatility Risk Premium
Jingfei Cheng
Department of Finance, School of Economics, Shanghai University, Shanghai, China
Email: cjf_26@126.com


Received January 2015

ABSTRACT
Volatility is an important variable in the financial market. We propose a model-free implied volatility method to measure the volatility and test the volatility risk premium. The model-free implied volatility does not depend on the option pricing model, and extracts information from all the option contracts. We provide empirical evidence from the S & P 500 index option that model-free implied volatility is more accurate to forecast the future volatility and the volatility risk premium does not exist.
Keywords:
Model-Free Implied Volatility, Volatility Forecasting, Volatility Risk Premium

1. Introduction
During the past twenty years, volatility forecasting and volatility risk premium are becoming more and more important in financial engineering. Many works have been found in the theoretical and practical fields. Engle [1] proposed the first ARCH model in 1982, Bollerslev [2] and Taylor [3] added the old conditional variance into the new estimation of conditional variance, which is the generalized autoregressive conditional heteroskedasticity model (GARCH). Model-free implied volatility originated from the variance swap theory. Dupire [4] and Neuberger [5], Demeterfi, Derman, Kamal and Zou (DDKZ) [6] [7], Britten-Jones and Neuberger [8] expanded it further. When the underlying asset price jumps exist, Britten-Jones and Neuberger did not state explicitly. Since the jump is important in financial asset prices, Jiang and Tian [9] proved the conclusions from Britten- Jones and Neuberger remain valid when the price jumps exist, thus ensuring the generalizability of this method. Jiang and Tian [10] also demonstrated that DDKZ’s variance fair value and Britten-Jones and Neuberger’s yields squares are the same. Besides, they came to a conclusion that the model-free implied volatility has more information content than the Black-Scholes implied volatility. In this paper, the theories of the model-free implied volatility and the time series model are used in the American S & P500 index option market. We compare model-free implied volatility method with GARCH model from the empirical aspect and test the volatility risk premium.
2. Model-Free Implied Volatility
The squared volatility can be expressed as the integration of call option forward prices [8]:
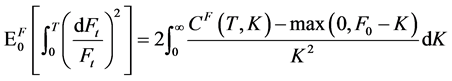 (1)
(1)
where,  denotes the forward price of the underlying asset at time t.
denotes the forward price of the underlying asset at time t.  denotes the forward price of the call option at time 0, and K is the strike price.
denotes the forward price of the call option at time 0, and K is the strike price.
Through the prices of current option contracts, we can get the long-term expectation for the market volatility. The Chicago Board Options Exchange began to use this new approach to calculate S & P500 volatility index (VIX) in 2003.
In Equation (1), strike prices range from zero to infinite, and expiration dates of different options are the same. But in the real market, strike prices are discrete and finite, and then Equation (1) can be simplified to Equation (2):
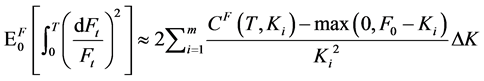 (2)
(2)
where,  ,
, 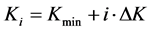 ,
,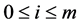 .
.
The above process will bring two types of errors: truncation errors and discretization errors.
Truncation errors derive from the limited range of strike prices. Strike prices are within a certain range of underlying asset prices. Jiang and Tian [9] discovered that if cut-off points (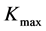 or
or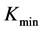 ) are far from
) are far from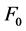 , truncation errors are small. Truncation errors are negligible if
, truncation errors are small. Truncation errors are negligible if 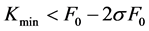 or
or . Otherwise, volatilities of cut-off points should be used to replace those out of the strike price interval
. Otherwise, volatilities of cut-off points should be used to replace those out of the strike price interval , which means volatilities outside the interval are constant.
, which means volatilities outside the interval are constant.
Discretization errors derive from discrete strike prices. The interval  between each strike price may vary, but will not tend to zero. When
between each strike price may vary, but will not tend to zero. When 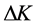 is smaller, the discrete errors is smaller. Jiang and Tian [9] found that the discretization error can be ignored when
is smaller, the discrete errors is smaller. Jiang and Tian [9] found that the discretization error can be ignored when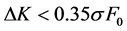 , where
, where  is the realized volatility of the underlying assets within the remaining maturity of the option. If
is the realized volatility of the underlying assets within the remaining maturity of the option. If
3. Volatility Forecasting
Since S & P500 index option is very active during past ten years, we choose all the call options (26 days to the expiration date) from February 2006 to February 2014.
Before the calculation of model-free implied volatility, errors should be analyzed at first. The realized volatility 

As Figure 1 shows, the horizontal axis represents observation sequence, and the vertical axis represents
the multiple: for every highest strike price 



In the sample, the strike price interval 


Based on above analysis, discretization errors and truncation errors are relatively small for the sample, only a small part needs to use interpolation.
For a better comparison, we estimate the GARCH model using dynamic scrolling windows, and take the out of sample forecasting method [11].
According to the AIC criterion, we get the GARCH(1,1) model:
where,
We give three volatility sequences in Figure 3. The horizontal axis represents observation days and the
Figure 1. Multiple for strike price (unit:
Figure 2. Corresponding 
vertical axis represents volatility values.
From Table 1 we can see these three volatility sequences present positive skewness, and each kurtosis is great. In the description of extreme volatility values, the maximum of model-free implied volatility 

4. Volatility Risk Premium
The deviation of implied volatility can be expressed as
If the deviation is significantly greater than zero, the implied volatility is always underestimated. People pay lower prices to buy options. Investors get excess earnings by purchasing options. There is a positive volatility risk premium.
Conversely, if the deviation is significantly less than zero, it means implied volatility is always overestimated. When people buy options, the option prices are higher than the theoretical prices. Investors pay a higher premium and there is a negative volatility risk premium.
During the remaining term of the option, volatility determines the option price. But volatility is unknown at the time of option pricing and people need to estimate it. Empirical analysis in the previous section has shown that the model-free implied volatility is more effective to reflect people’s expectations for the future. It is more reasonable to use the model-free implied volatility method to test the volatility risk premium.
We can see from Table 2 that for options with remaining term of 26 days, the negative deviation of implied
Figure 3. Volatility sequences.
Table 1. Descriptive statistics.
Table 2. The deviation of implied volatility.
volatility is not significant. We cannot reject the null hypothesis that the volatility risk premium does not exist.
5. Conclusions
Information in the financial markets are updating every moment. GARCH model uses only the historical yields information. The model free implied volatility considers the latest information in the current markets from all the option contracts, including strike prices, option prices, the remaining term of options, the risk-free interest rate and underlying asset prices.
After empirical research with different models in the American S & P500 index option market, we found that, as a result of the model-free implied volatility method not relying on the option pricing model and extracting information from all the option contracts, the information content of the model-free implied volatility is more than GARCH model volatility. The model-free implied volatility is more effective to predict the future realized volatility. The volatility risk premium does not exist for options with remaining term of 26 days, and Investors avoid paying a higher premium in option trading.
Cite this paper
Jingfei Cheng, (2015) Volatility Forecasting and Volatility Risk Premium. Journal of Applied Mathematics and Physics,03,98-102. doi: 10.4236/jamp.2015.31014
References
- 1. Engle, R.F. (1982) Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica, 50, 987-1007. http://dx.doi.org/10.2307/1912773
- 2. Bollerslev, T. (1986) Generalized Autoregressive Conditional Heteroskedasticity. Journal of Econometrics, 31, 307- 327. http://dx.doi.org/10.1016/0304-4076(86)90063-1
- 3. Taylor, S.J. (1986) Modeling Financial Time Series. John Wiley & Sons, New York.
- 4. DuPire, B. (1994) Pricing with a Smile. Risk, 7, 18-20.
- 5. Neuberger, A. (1994) The Log Contract. Journal of Portfolio Management, 20, 74-80. http://dx.doi.org/10.3905/jpm.1994.409478
- 6. Demeterfi, K. (1999) A Guide to Volatility and Variance Swap. Journal of Derivatives, 6, 9-32. http://dx.doi.org/10.3905/jod.1999.319129
- 7. Demeterfi, K. (1999) More than You Ever Wanted to Know about Volatility Swaps. Goldman Sachs Quantitative Strategies Research Note.
- 8. Britten-Jones, M. and Neuberger, A. (2000) Option Prices, Implied Price Processes, and Stochastic Volatility. Journal of Finance, 55, 839-866. http://dx.doi.org/10.1111/0022-1082.00228
- 9. Jiang, G.J. and Tian, Y.S. (2005) The Model-Free Implied Volatility and Its Information Content. The Review of Financial Studies, 18, 1305-1342. http://dx.doi.org/10.1093/rfs/hhi027
- 10. Jiang, G.J. and Tian, Y.S. (2007) Extracting Model-Free Volatility from Option Prices: An Examination of the VIX Index. Journal of Derivatives, 14. http://dx.doi.org/10.3905/jod.2007.681813
- 11. Tsay, R.S. (2005) Analysis of Financial Time Series. John Wiley & Sons. http://dx.doi.org/10.1002/0471746193






