Journal of Applied Mathematics and Physics
Vol.03 No.01(2015), Article ID:53600,6 pages
10.4236/jamp.2015.31013
Profile Design and Numerical Calculation of Instantaneous Flow Rate of a Gerotor Pump
Hao Liu1*, Jae-Cheon Lee1, Alex Yoon2, Sang-Tae Kim2
1Department of Mechanical and Automotive Engineering, Keimyung University, Daegu, South Korea
2Automotive Motor Biz. Division, LG Innotek, Incheon, South Korea
Email: *liuhao@kmu.ac.kr


Received December 2014

ABSTRACT
Gerotor pump is a special kind of internal rotary pump, which contains a trochoid profile (commonly called as cycloid). Generation of trochoid is normally realized by external rolling method, namely a circle rotating on a fixed circle without slipping. This paper proposes derivative process of the trochoid profile by means of internal rolling method, which is that internal surface of a circle contacts with a fixed circle and rotates around it without slipping. Moreover the instantaneous flow rate can be obtained by numerically calculating the change ratio of area between the inner and outer rotors in the outlet region of the gerotor pump, which avoids to complicatedly derivative process.
Keywords:
Gerotor Oil Pump, Trochoid, Internal Rolling Method, Instantaneous Flow Rate

1. Introduction
Gerotor oil pump belongs to a kind of internal gear pump, which is a positive displacement pump. Compared with an external or internal gear pump, it keeps advantages of less components, simple structure, compact size, low noise, and low ripple of flow rate. Therefore it is widely used in applications of lubricating system of on-road or off-road engines [1].
Gerotor oil pump mainly consists of an inner rotor, an outer rotor, housing in which inlet (suction) and outlet (delivery) ports are machined. The inner rotor lies inside the outer rotor and it positions itself at a fixed eccentricity from the outer rotor inside the housing. The inner rotor has normally one tooth, or more than one tooth in some special gerotor pumps, less than the outer rotor. Input torque is to drive the inner rotor, and the outer rotor rotates with it since they contact each other at less several points of their geometrical profiles. For Gerotor oil pump, the inner and outer rotors have a special type of conjugate profiles which always ensure contact of the inner and outer rotors. The easiest way to generate the profile of a gerotor oil pump is to let a circle rotate, without slipping, on a straight line or another circle. Table 1 shows nine different class of curves which can be used to generate the gerotor profile [2].
Table 1. Nine possible curves for profile generation.
The trochoid profile, which refers to any of the cycloid including the curtate cycloid and the prolate cycloid, is widely used in profile generation of gerotor pumps [3]-[5]. Based on profile generation, some researches about performance analysis, such flow/pressure ripple, calculation of flow rate, and noise level and so on, have been done by using CFD modeling [2] [6] [7], AMESim [5], or experiment [8]. This paper focuses on generation of trochoid profile by another proposed way, and analyzes basic parameters of the trochoid profile.
2. Profile Design Inner and Outer Rotors
The trochoid profile used in the inner rotor of a gerotor pump is the equidistant curve of the trochoid, and the profile of the outer rotor is the conjugate profile with partial arc of circles, whose radius is equal to the above equidistant value. In geometry, if family circles are drawn with the center of points located on the trochoid, the internal enveloping lines of family circles form the profile of the inner rotor. By this method, the parameter equation of the profile of the inner rotor can be obtained.
2.1. Formation of Trochoid
When a rolling circle with the radius of r2 rolls without slipping around a fixed circle, called as a base circle, with the radius of r1, the curve called as trochoid is the locus of an arbitrate fixed point, C, on the circle (inside the circle, on its circumference, or outside). This is the external rolling method (the rolling circle rolls outside a fixed base circle) to form a trochoid, which is shown in Figure 1. Meanwhile, the internal rolling method (the rolling circle rolls inside a fixed base circle) is also able to generate a trochoid, if the radius of the rolling circle, r2, is greater than that of the base circle, r1, and both circles rolls with internal tangent (refer to Figure 2). The internal rolling method is used in this research to develop the profile of the inner rotor.
Figure 2 illustrates how to form a trochoid by using the internal rolling method. In the figure, O1 and O2 are the centers of the base circle and the rolling circle, respectively. When both circles rolls without slipping at the contact point, P, an arbitrary fixed point, C, on the rolling circle forms a locus on the plane fixed with the base circle. This locus, C1, is just the trochoid.
In order to obtain profile, a fixed coordinates system Sf (O1, x, y) is built, whose origin locates on the center of the base circle O1 and whose x-axis passes through the contact point P. A rotary coordinates system S1 (O1, x1, y1) is built too, whose origin is the point O1 and which is fixed with the base circle. And another rotary coordinates system S2 (O2, x2, y2) is built, whose origin is the point O2 and which is fixed with the rolling circle. And the point C is on the x2-axis.
Since there is no slipping between the rolling circle and the base circle, when the base circle rotates φ1 around its center the rolling circle accordingly rotates φ2 around its center too. Moreover the following relation exists duo to no slipping.
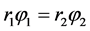 (1)
(1)
After determination of r1 and r2, the shape of trochoid depends on the ratio of the radius of the rolling circle r2 to the distance L from the point C to the center of the rolling circle O2. The ratio is defined as curtate ratio.
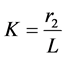 (2)
(2)
Let k be the reciprocal of K, so
 (3)
(3)
Figure 1. Formation of trochoid by using external rolling method.
Figure 2. Formation of trochoid by using internal rolling method and meshing of inner and outer rotors.
According to coordinate transformation theory, the transformation matrix from the coordinates S2 to the coordinates S1 is as below.
 (4)
(4)
The locus of point C in the rotary coordinates S2 is
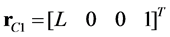 (5)
(5)
And the locus of point C in the rotary coordinates S1 is just the trochoid, which can be expressed by the following matrix form.
 (6)
(6)
Rewrite the above locus equation of the trochoid by the form of rectangular coordinates, that is
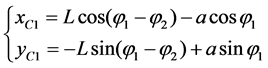 (7)
(7)
2.2. Profiles of Inner and Outer Rotors
According to the formation of trochoid, the relatively instantaneous center between the base circle and the rolling circle as their rolling without slipping is the tangential point P. Thus the line PC is also the normal for the curve C1, shown as in Figure 2. Family circles (or considered as the cutter circle as manufacture of the inner rotor) are drawn with the center of points located on the trochoid C1 and the radius of R, and then the internal enveloping lines of family circles is the equidistant curve of the trochoid C1, i.e. the profile of the inner rotor. The profile of the outer rotor is the part of its conjugate arc.
Let the angle between the line O2C and the normal PC of trochoid as θ, therefore the sine theorem can be applied in the triangle ΔPCO2 as follows.
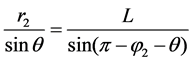 (8)
(8)
The above equation cam be simplified by using Equation (3).
 (9)
(9)
This equation is called the meshing equation of trochoid gears, which can be rewritten as
 (10)
(10)
As mentioned previously, the profile of inner rotor is the equidistant curve of the trochoid and the profile of outer rotor is the arc with the radius of R. The meshing point M locates on the common normal PC. The profile equation of inner rotor can be induced by using the form of complex vector in [9], and its profile equation in rectangular coordinates is directly given as.
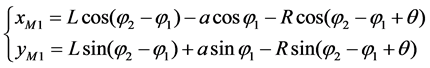 (11)
(11)
Figure 3 shows the profile of inner rotor (the blue solid curve), where R = 8.5 mm. The profile of outer rotor contains two parts: one is the partial arcs of magenta solid circles in Figure 3, and other is the root circle of outer rotor, marked in black color in Figure 3.
3. Numerical Calculation of Flow Rate
3.1. Determination of Area Variation
With the inner rotor rotating, oil in the chambers enclosed by the inner and outer rotors in the outlet region are squeezed continuously, so it can be pumped out from the pump. The flow rate is determined by variation of area
Figure 3. Profiles of inner and outer rotors (Z1 = 7, a = 2.5 mm, r1 = 17.5 mm, r2 = 20 mm, K = 0.7, R = 8.5 mm).
between the inner and outer rotors in the outlet region. According to the profiles of inner and outer rotors given in Section 2, area variation with rotation can be obtained. The accurately analytical calculation equations of flow rate is given in [3] [9], which are presented by rather complicated differential-integration form. Another way to calculate the flow rate of the gerotor pump is directly to compute, by means of coordinates of the inner and outer rotors, the area in the outlet region at each rotating angle of the inner rotor.
Figure 4 shows area in the outlet region of the pumps with six teeth inner rotor, when the inner rotor rotates by the angle corresponding to one tooth. It is easy to understand how the area successively varies from the maximal value to minimal value.
3.2. Pulsation of Flow Rate
After calculation of the area between the inner and outer rotors in the outlet region, the area ratio with respect to rotating angle is accordingly obtained. The product of the area change ratio and the width of rotors is just the instantaneous flow rate. Now the pulsation of flow rate is investigated by considering the instantaneous flow rate during the period of one tooth rotation of the inner rotor. Three gerotor pumps have 6, 7, and 8 tooth numbers (Z1) of the inner rotor, and their rated flow rates are same. In order to compare their pulsation of flow rate, the instantaneous flow rates are normalized to mean flow rates, which show in Figure 5. It is seen from the figure that increasing the tooth number can reduce flow rate ripple. And one important point is that the even tooth number of the inner rotor causes lower flow ripple. Their pulsation coefficients are 4.4%, 10.1%, and 2.2%, respectively, by using following equation in [10].
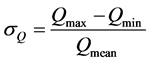 (12)
(12)
4. Conclusion
Gerotor pump is increasingly used in applications of automotive, such as lubrication system. Generation of gerotor profile by using internal rolling method is focused in the paper. Coordinates of gerotor profile of inner and outer rotors are derived according to meshing of inner and outer rotors. It is also investigated how to calculate instantaneous flow rate by computing decreasing of area between inner and outer rotors in the outlet region. The paper shows a way to generate profile and a numerical method to calculate instantaneous flow rate.



Figure 4.Area variation with one tooth rotating angle (2π/Z1) of even tooth (Z1 = 6) of inner rotor.
Figure 5. Pulsation of flow rate.
Acknowledgements
This work was supported by the Ministry of Trade, Industry and Energy (MOTIE) and Korea Institute of Advancement of Technology (KIAT) through the Center for Automotive Mechatronics Parts (CAMP) at Keimyung University.
Cite this paper
Hao Liu,Jae-Cheon Lee,Alex Yoon,Sang-Tae Kim, (2015) Profile Design and Numerical Calculation of Instantaneous Flow Rate of a Gerotor Pump. Journal of Applied Mathematics and Physics,03,92-97. doi: 10.4236/jamp.2015.31013
References
- 1. Lingeswaramurthy, P., Jayabhaskar, J., Elayaraja, R. and Suresh Kumar, J. (2011) Development of Analytical Model for Design of Gerotor Oil Pump and Experimental Validation. SAE Int. J. Engines, 4, 441-449. http://dx.doi.org/10.4271/2011-01-0402
- 2. Jamadar, M., Jose, A., Ramdasi, S. and Marathe, N. (2013) Development of In-house Competency to Build Compact Gerotor Oil Pump for High Speed Diesel Engine Application. SAE Technical Paper, 2013-01-2738. http://dx.doi.org/10.4271/2013-01-2738
- 3. Mancò, S., Nervegna, N., Rundo, M., Armenio, G., Pachetti, C. and Trichilo, R. (1998) Gerotor Lubricating Oil Pump for IC Engines. SAE Technical Paper, 982689. http://dx.doi.org/10.4271/982689
- 4. Fabiani, M., Mancò, S., Nervegna, N., Rundo, M., Armenio, G., Pachetti, C. and Trichilo, R. (1999) Modelling and Simulation of Gerotor Gearing in Lubricating Oil Pumps. SAE Technical Paper, 1999-01-0626. http://dx.doi.org/10.4271/1999-01-0626
- 5. Mancò, S., Nervegna, N. and Rundo, M. (2000) Effects of Timing and Odd/Even Number of Teeth on Noise Generation of Gerotor Lubricating Pumps for IC Engines. SAE Technical Paper, 2000-01-2630. http://dx.doi.org/10.4271/2000-01-2630
- 6. Zhang, D., Perng, C. and Laverty, M. (2006) Gerotor Oil Pump Performance and Flow/Pressure Ripple Study. SAE Technical Paper, 2006-01-0359. http://dx.doi.org/10.4271/2006-01-0359
- 7. Elayaraja, R., Lin-geswaramurthy, P. and Govindarajan, S. (2009) Performance of Gerotor Oil Pump for an Automotive Engine-Prediction Using CFD Analysis and Experimental Validation. SAE Technical Paper, 2009-28-0007. http://dx.doi.org/10.4271/2009-28-0007
- 8. Srinivasan, S., Kumar, J.S., Vijayakumar, K. and Venkataraman, P. (2012) Performance Improvement of Automotive Oil Pump to Operate at High Temperatures Employed in Modern Diesel Engines. SAE Technical Paper, 2012-01-0428. http://dx.doi.org/10.4271/2012-01-0428
- 9. Xu, X.Z. (2005) Theoretical Research and Simulation of Internal Cycloid Pump. Ph.D Dissertation, Dongnan University, Nanjing.
- 10. Rabie, M.G. (2009) Fluid Power Engineering. McGraw-Hill.
Nomenclature
NOTES
*Corresponding author.










