Received December 2014

ABSTRACT

The compressible miscible displacement in a porous media is considered in this paper. The problem is a nonlinear system with dispersion in non-periodic space. The concentration is treated by a characteristics collocation method, and the pressure is treated by an orthogonal collocation method. Optimal order estimates are derived.

Keywords:

Compressible, Dispersion, Characteristics Collocation, Non-Periodic

1. Introduction

The mathematical controlling model for compressible miscible displacement in porous media with dispersion is given by

(1)

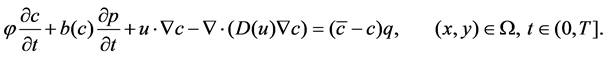(2)

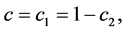
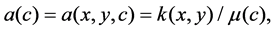
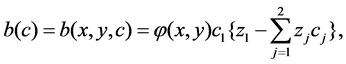
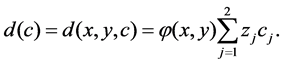
where 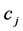and denote the concentration and constant compressibility factor for the i component of the fluid mixture respectively. Let 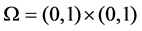with the boundary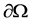, 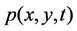the pressure in the mixture, u is the Darcy velocity of the fluid, and 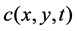is the relative concentration of the injected fluid. and 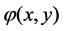are the permeability and the porosity of porous media, is the viscosity of the fluid. 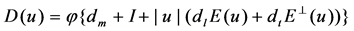are the molecular dissipation and dispersion terms, where 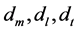are the molecular dissipation, longitudinal and tangential dispersion coefficients. I is a 2 unit matrix, is a matrix representing orthogonal projection along the velocity vector and is the complementary projection. q and etc. refer to the definition and significance of [1] [2].

We shall assume that no flow occurs across the boundary

(3)

where v is the outer normal to, and the initial conditions are

(4)

The compressible flow problems are strongly nonlinear coupling system for partial differential equations of two different types, and we consider the system with dispersion in non-periodic space, so these factors lead to many difficulties for convergence analysis of algorithms. The collocation methods are widely used for solving practice problems in engineering due to its easiness of implementation and high-order accuracy. But the most parts of mathematical theory focused on one-dimensional or two-dimensional constant coefficient problems [3] [4]. [5] proposes the collocation method of two-dimensional variable coefficients elliptic problems. The characteristics collocation scheme for the incompressible flow is given in [6]. The characteristics finite element method for the compressible miscible flow is proved in [7]. In the paper we shall use different technique to treat different types of equations, the orthogonal collocation methods solve the pressure equation and the characteristics collocation scheme approximate the concentration equation. We develop some technique to analyze convergence of these algorithms for this strongly nonlinear system with dispersion in non-periodic space. Finally we can obtain the optimal order error estimate. We shall assume the coefficients etc. and their partial derivatives have positive upper and lower bounds independently as well as smoothly. Throughout, the symbols K and will denote, respectively, a generic constant and a generic small positive constant.

The organization of the rest of the paper is as follows. In Section 2, we will present the formulation of the characteristic collocation scheme for nonlinear system (1) (2). In Section 3, we will analyze convergent rate of the scheme defined in Section 2.

2. Characteristic Collocation Scheme (CCS)

2.1. Preliminaries

In this subsection, we will give some basic notations and definition for the characteristics collocation methods, which will be used in this article. We make the partition of the domain, which is quasi-uniform and equally spaced rectangular grid by and steps along x-direction and y-direction. Let

.

Define function spaces as follows:

,

where denotes the set of polynomials of degree, similarly we can define. Let then let be the spaces of piecewise Hermite bicubics.

Next, we take four Gauss points as collocation points in, and, , where. Introduce the following summation notation:

Let be the interpolation operator of piecewise Hermite bicubics on, and and be the interpolation operators of piecewise Hermite bicubics in x and in y, respectively, which may be defined by for sufficiently smooth function v.

2.2. CCS

In this subsection we will present the fully discrete characteristic collocation scheme for nonlinear system (1) (2) with dispersion term in non-periodic space. At first time can be discretized:

We consider the concentration Equation (2), let, and the characteristic direction associated with the operator is denoted by, hence.

The Equation (2) can be put in the form

(5)

For (5), we use a backward difference quotient for along the characteristic line:

(6)

where.

So we can obtain the following discrete equation:

Now that use the interpolation operator and the Gauss points, we give the fully discrete characteristics collocation scheme (CCS):

(7)

(8)

(9)

and (10)

for computed in the order: at first can be computed from (8), then from (10) and (9) we can solve. Because the system is non-periodic, we need to do a continuation as shown in Figure 1.

We can understand the following method intuitively from above schematic diagram. When is through the boundary, we will do continuation according to specular reflection method, namely when is outside, we do the normal from to, and the normal intersects at. Then we do inner normal at, and we choose point so as to, and the value of replaces the one of, in this way c and C etc. functions are certain meaning. Because c satisfies (3), the continuation is logical [7].

3. Convergence Analysis

In this section we consider the existence and uniqueness of the numerical solution, and obtain the optimal error estimate. CCS (8) (9) can be rewritten as the discrete Galerkin method given by [3] [6] [8]

(11)

(12)

We can get the following convergence conclusion for the above numerical Scheme (11) (12).

Theorem 3.1 Suppose, then there exists a constant K such that, for h sufficiently small,

Proof: Let Subtracting (11) from the discrete Galerkin scheme of (1), we obtain the pressure error equation

(13)

where, and choosing the test function in (13), and the right terms can be denoted by in turn. For error estimate, we shall need an induction hypothesis. We assume that

(14)

We start this induction by seeing that for h sufficiently small. We shall check that if, (14) is right at the end of the proof. So we get the error estimate of the pressure [6] [8].

(15)

for sufficiently small.

Next we will consider the concentration equation, subtracting (12) from the discrete Galerkin scheme of (2),

(16)

To obtain optical estimate for we choose as test function in (16), and we denote the resulting right-hand side terms by. And we need another induction hypothesis, we assume that

(17)

If, we can start the induction by (15) to get,

for h sufficiently small and. We shall check that if, (17) is right at the end of the proof. Similar to the discussion in [6] [8], and the relations (15) (17) and Gronwall lemma, we can get

And it can be combined with (15) to show that

.

At last we shall check the induction hypotheses (14) and (17)

for h sufficiently small , and the proof is complete.

Acknowledgements

We thank the fund “Basic Subjects Fund of China University of Petroleum (Beijing) (KYJJ2012-06-04)”.

Cite this paper

Ning Ma,Xiaofei Lu, (2015) Characteristics Collocation Method of Compressible Miscible Displacement with Dispersion. Journal of Applied Mathematics and Physics,03,86-91. doi: 10.4236/jamp.2015.31012

References