Journal of Applied Mathematics and Physics
Vol.03 No.01(2015), Article ID:53597,5 pages
10.4236/jamp.2015.31011
B-Spline Approximation of Ship Waves on the Free Surface
Fang Li, Hui Li, Huilong Ren
College of Shipbuilding Engineering, Harbin Engineering University, Harbin, China
Email: lifang199011@163.com


Received December 2014

ABSTRACT
We consider the problem of a ship advancing in waves. In this method, the zone of free surface in the vicinity of body is discretized. On the discretized surface, the first-order and second-order derivatives of ship waves are represented by the B-Spline formulae. Different ship waves are approximated by cubic B-spline and the first and second order derivates of incident waves are calculated and compared with analytical value. It approves that this numerical method has sufficient accuracy and can be also applied to approximate the velocity potential on the free surface.
Keywords:
Cubic B-Spline, Free Surface Grid Division, Approximation of Incident Wave

1. Introduction
In the method for hydrodynamic analysis of floating bodies with forward speed, due to the complex boundary condition on the free surface, the integral equation involves not only the unknown velocity potential but also its first-order and second-order derivatives on the free surface. Unlike classical methods in which a waterline integral is present by using Stokes’ theorem, we apply directly the free-surface condition so that the troublesome waterline integral is avoided. The first- and second-order derivatives of the velocity potential in this new method are then approximated using B-Spline method.
In this paper, the incident wave on free surface is approximated by cubic B-spline and the relationship between incident wave and its first-order and second-order partial derivatives are derived and compared with the analytical value.
This method is approved to have sufficient accuracy and can be also applied to approximate the velocity potential on the free surface.
2. Fundamental Theory of B-Spline
2.1. Definition of B-Spline Curves and Surfaces
Let the knot vector 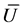 be a set of m + 1 non-decreasing numbers, u0 < = u2 < = u3 < = ... < = um. We define the kth degree B-spline curve as Equation (1) [1]:
be a set of m + 1 non-decreasing numbers, u0 < = u2 < = u3 < = ... < = um. We define the kth degree B-spline curve as Equation (1) [1]:
 (1)
(1)
where 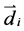 is control vertices, n + 1 is the number of control vertices,
is control vertices, n + 1 is the number of control vertices, 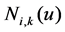 is the kth degree B-spline basis functions.
is the kth degree B-spline basis functions.
The ith B-spline basis function of degree k, written as , is defined by Cox-de Boor recursion formula as Equation (2) [2]
, is defined by Cox-de Boor recursion formula as Equation (2) [2]
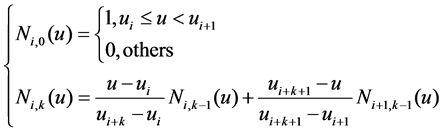 (2)
(2)
In the same way, we define the B-spline surface by B-spline tensor product expansion as Equation (3) [3]
 (3)
(3)
where  is the kth degree B-spline basis functions,
is the kth degree B-spline basis functions,  is the lth degree B-spline basis functions,
is the lth degree B-spline basis functions, 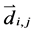 is control vertices, m + 1 and n + 1 are the number of control vertices in u and v parametric directions respectively, u and v are two independent parameters which monotonically increase along the respective parametric spaces.
is control vertices, m + 1 and n + 1 are the number of control vertices in u and v parametric directions respectively, u and v are two independent parameters which monotonically increase along the respective parametric spaces.
2.2. The de Boor Algorithm
Given a clamped B-spline curve of degree k defined by n + 1 control points 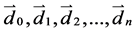 and m + 1 knots u0 = u1 = ... = uk = 0, uk+1, uk+2, ..., um−k−1, um−k = um−k+1 = ... = um = 1, we can compute the point on the B-spline curve by the de Boor algorithm as Equation (4) [2]
and m + 1 knots u0 = u1 = ... = uk = 0, uk+1, uk+2, ..., um−k−1, um−k = um−k+1 = ... = um = 1, we can compute the point on the B-spline curve by the de Boor algorithm as Equation (4) [2]
 (4)
(4)
where

 (5)
(5)
2.3. Derivatives of B-Spline Curves and Surfaces
Given a clamped B-spline curve of degree k, we can compute r order derivatives  as Equation (6) [2]:
as Equation (6) [2]:
 (6)
(6)
where
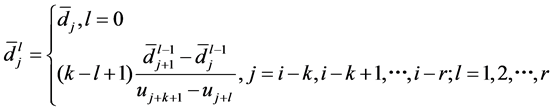 (7)
(7)
2.4. B-Spline Curves and Surfaces Approximation
B-spline curve approximation can be stated as the problem of constructing a B-spline curve passing through a set of fixed points



where 
3. The Details of Study Method
3.1. Approximation of Incident Wave on the Free Surface
We choose a set of points 

where A is the amplitude of the incident wave, k is wave number, 



Let 

When the incident wave is given as

We choose cubic B-spline to approximate the free surface. The free surface is divided into two patches, then each patch is described by cubic B-spline tensor product expansion as Equation (10). Figure 2 shows the wave surface approximated by cubic B-spline

3.2. Calculation of the Derivatives of Incident Wave Based on B-Spline
The points on the surface can be described as Equation (11):

The first and second order partial derivatives of incident wave 



We can calculate the value of



Figure 1. The distribution of points on the free surface.
Figure 2. The wave surface approximated by cubic B-spline.
tion 2.2 and 2.3. Then the value of and 



3.3. Approximation of Different Incident Wave on The free Surface
We choose the same points 



Then we use the cubic B-spline to approximate the free surface as we do in Section 3.1. Figure 3 show the wave surface approximated by cubic B-spline.
Then we can calculate the value of 


In the same way, the value of 

Figure 3. The wave surface approximated by cubic B-spline at
Table 1. Computed values and comparison to the analytical value at v = 0.5.
Table 2. Computed values and comparison to the analytical value at u = 0.1.
value of 


4. Conclusion
In this paper, we adopt cubic B-spline approximating the free surface in different incident waves, calculate the first and second order derivatives of incident wave based on B-spline theory and compare the numerical value to the analytical value. This method is approved to have sufficient accuracy but it depends on the selection of points. In addition, it also can be applied to approximate the velocity potential on the free surface.
Acknowledgements
This paper is funded by the International Exchange Program of Harbin Engineering University for Innovation- oriented Talents Cultivation and MOST 2011CB013703 plan.
Cite this paper
Fang Li,Hui Li,Huilong Ren, (2015) B-Spline Approximation of Ship Waves on the Free Surface. Journal of Applied Mathematics and Physics,03,81-85. doi: 10.4236/jamp.2015.31011
References
- 1. Gordon, W.J. and Riesenfeld, R.F. B-Spline Curves and Surfaces [A].
- 2. De Boor, C. (1972) On Calculation with B-Splines. J. Approx. Theory.
- 3. Hoschek, J. and Lasser, D. (1993) Fundamentals of Computer Aided Geometric Design. A K Peters.
- 4. Farin, G. (1993) Curves and Surfaces for Computer Aided Geometric Design. Academic Press.





