Journal of Applied Mathematics and Physics
Vol.03 No.01(2015), Article ID:53587,6 pages
10.4236/jamp.2015.31010
Expansion by Laguerre Function for Wave Diffraction around an Infinite Cylinder
Mingdong Lv1, Hui Li1, Huilong Ren1, Xiaobo Chen2
1College of Shipbuilding Engineering, Harbin Engineering University, Harbin, China
2Bureau Veritas Research Department, Singapore City, Singapore
Email: 1213730780@qq.com


Received December 2014

ABSTRACT
We consider a vertical circular cylinder on which the vertical variation of water diffraction waves is to be represented by a series of Laguerre functions 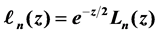 using Laguerre Polynomials
using Laguerre Polynomials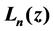 . The variation is assumed to be of the form
. The variation is assumed to be of the form  with the integer n depending on the radius of cylinder. Generally, the integer n increases for a cylinder of larger diameter. The usual approximation by Laguerre functions is extended by introducing a scale parameter. The convergence of Laguerre series is then dependent on the value of the scale parameter s. The analytical and numerical computations of series coefficients are performed to study the number of series terms to keep the same accuracy. Indeed, the choice of integer n depends on the scale parameter. Furthermore, diffraction waves generated by a semi-sphere inside the cylinder are evaluated on the cylinder surface. It is shown that the approximation by Laguerre series for diffraction waves on the cylinder is effective. This work provides important information for the choice of the radius of control surface in the domain decomposition method for solving hydrodynamic problems of body-wave interaction.
with the integer n depending on the radius of cylinder. Generally, the integer n increases for a cylinder of larger diameter. The usual approximation by Laguerre functions is extended by introducing a scale parameter. The convergence of Laguerre series is then dependent on the value of the scale parameter s. The analytical and numerical computations of series coefficients are performed to study the number of series terms to keep the same accuracy. Indeed, the choice of integer n depends on the scale parameter. Furthermore, diffraction waves generated by a semi-sphere inside the cylinder are evaluated on the cylinder surface. It is shown that the approximation by Laguerre series for diffraction waves on the cylinder is effective. This work provides important information for the choice of the radius of control surface in the domain decomposition method for solving hydrodynamic problems of body-wave interaction.
Keywords:
Laguerre Function, Wave Diffraction around an Infinite Cylinder

1. Introduction
The Rankine source panel method needs a large number of panels due to panelizing the free surface as well as a damping zone avoiding the reflected wave from the sides of a numerical fluid domain. So a control surface can be introduced to divide the fluid domain into two subdomains by a control surface. This surface separates the problem into two problems: 1) the interior one in which the ship is of any form, the Green function is Rankine source Green function; 2) the exterior one in which the shape of the control surface is known and velocity potential is assumed to be known. It brings two important benefits: area to be discretized becomes smaller; no need to introduce the damping zone [1].
A circular cylinder is adopted as control surface. The vertical variation of water diffraction wave is assumed to be the form 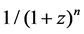 which is represented by a series of Laguerre functions
which is represented by a series of Laguerre functions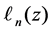 . Laguerre functions
. Laguerre functions  which are defined by Laguerre polynomials
which are defined by Laguerre polynomials 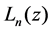 are a system of orthogonal functions on the interval [0, ¥] [2]. It plays an important role in approximation and interpolation.
are a system of orthogonal functions on the interval [0, ¥] [2]. It plays an important role in approximation and interpolation.
The purpose of this paper is to validate the accuracy and convergence of Laguerre series and approximate the vertical velocity potential f on an infinite cylinder generated by a body. Section 2 introduces basis of Laguerre functions. Section 3 provides an analytical method to approximate the function 1/(1 + z)n and the velocity potential f by Laguerre functions. Section 4 uses some examples to investigate the convergence and accuracy of the method, and compares the result of Compass-Walcs-Basic.
2. The Basis of Laguerre Function
2.1. Laguerre Polynomials
The Laguerre polynomials are defined by the three-term recurrence relation
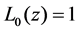 (1)
(1)
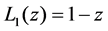 (2)
(2)
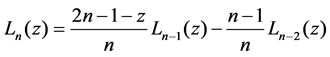 (3)
(3)
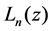 is called nth degree Laguerre polynomial [3].
is called nth degree Laguerre polynomial [3].
The Laguerre polynomials have some useful relations
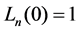 (4)
(4)
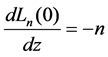 (5)
(5)
 (6)
(6)
By virtu3 of Equation (6), we can obtain Equation (7)
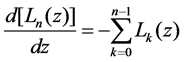 (7)
(7)
We define 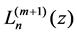 as Equation (8)
as Equation (8)
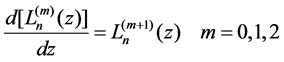 (8)
(8)
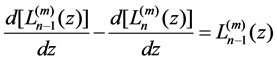
By virtue of Equation (9), we can obtain Equation (10)
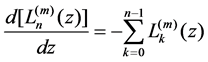
And the orthogonal relation
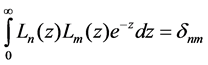
where 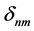
Furthermore it can be easily shown that

k is a real number.
2.2. Laguerre Functions and Scale Parameter s
We define nth degree Laguerre function 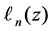
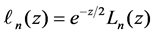
The Laguerre functions satisfy the orthogonal relation [3]:

where 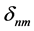
It is important to note that the Laguerre functions are well behaved. Indeed, the following properties are shown [3]:
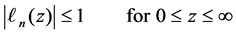
and
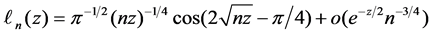
For n = 0, 1, 2
We can approximate a function by a series of Laguerre functions with scale parameter s:
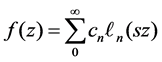
The Laguerre functions with scale parameter s also satisfy the orthogonal relation:
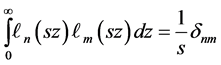
The coefficient cn are defined
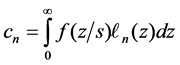
3. Numerical Approximation and Interpolation by Laguerre Functions
As the velocity potential ϕ is assumed to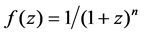
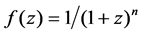
For function 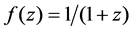

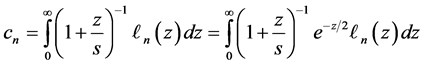
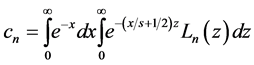
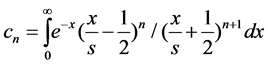
where we use the Equation (12) and Equation (24)
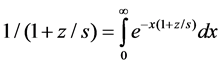
The coefficient cn can be calculated by Equation (23) in Gauss-Laguerre integration, see in Equation (25)

where xk is the kth distinct zero of nth Laguerre polynomial.
For function f(z) = 1/(1 + z)2
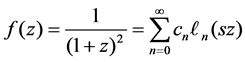
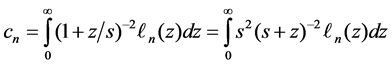

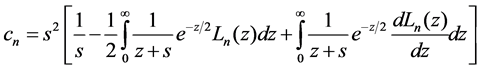
By virtue of Equation (7)
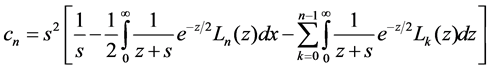
Then the integration in Equation (30) can be calculated in Equation (21), 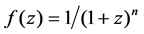


We suppose that the vertical velocity potential f(z) is continuous for z ≥ 0, where given function f(z) is only known numerically at every point. The Laguerre-Gauss interpolation is applied to approximate the f(z).
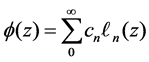
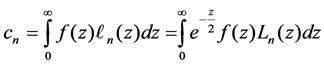

4. Numerical Results
In this section, we present some numerical results. The algorithm is implemented by using Intel Visual Fortran Composer XE 2011 and all calculations are carried out in a computer of CPU 3.30 GHz.
We first use Equation (23) to approximate function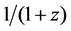
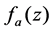

Then we use Equation (30) to approximate function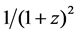
At last, we use Equation (31) to approximate function 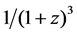
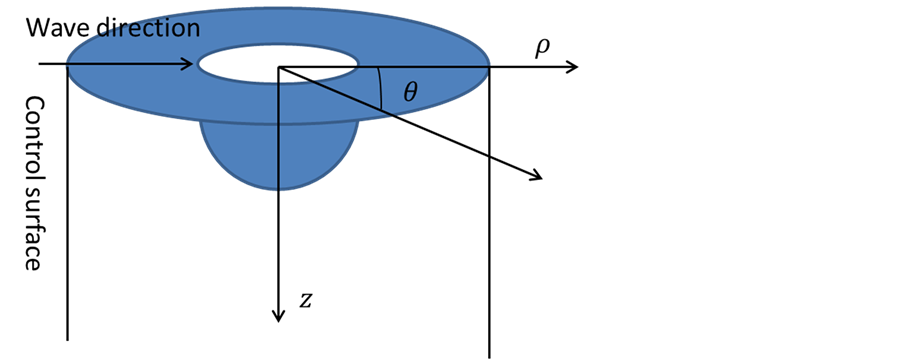
A semi-sphere is adopted as a body inside the cylinder to generate diffraction waves. The radius of semi- sphere is 2 m as well as cylinder is 2.5 m. The incident wave is in frequency of 0.6 rad/s, in height of 2 m. We prefer to approximate vertical variation with Equation (34) at θ is 0 rad/s, shown in Figure 1.
We compare the approximate results with results calculated by Compass-Walcs-Basic (CWB, a wave load software is developed by CCS), shown as Table 4.
5. Conclusion
In this note we presented a numerical method for interpolating vertical variation of water diffraction waves based on Laguerre functions. The convergence and accuracy is validated by approximating the functions
Table 1. Computed value and the relative errors at different values of z.
Table 2. Computed value and the relative errors at different values of z.
Table 3. Computed value and the relative errors at different values of z.
Table 4. Computed value and the relative errors at different values of z.
Figure 1. A semi-sphere in a cylinder.
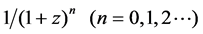
Cite this paper
Mingdong Lv,Hui Li,Huilong Ren,Xiaobo Chen, (2015) Expansion by Laguerre Function for Wave Diffraction around an Infinite Cylinder. Journal of Applied Mathematics and Physics,03,75-80. doi: 10.4236/jamp.2015.31010
References
- 1. Ten, I. and Chen, X.B. (2011) Zero Speed Rankine-Kelvin Hybrid Method. Bureau Veritas Research Department, 6.
- 2. Guo, B.-Y. and Wang, Z.-Q. (2007) Numerical Integration Based on Laguerre-Gauss interpolation. Comput. Methods Appl. Mech. Engrg, 196, 3726-3741. http://dx.doi.org/10.1016/j.cma.2006.10.035
- 3. Abramowitz, M. and Stegun, I.A. (1967) Handbook of Mathematical Functions. Dover Publications.
- 4. Keilson, J., Nunn, W. and Sumita, U. (1980) The Laguerre Transform. Center for Naval Analysys, 26-28.