Journal of Applied Mathematics and Physics
Vol.03 No.01(2015), Article ID:53576,16 pages
10.4236/jamp.2015.31007
Geometry of the Standard Model of Quantum Physics
Claude Daviau1, Jacques Bertrand2
1Le Moulin de la Lande, Pouillé-les-coteaux, France
215 Avenue Danielle Casanova, Saint-Gratien, France
Email: claude.daviau@nordnet.fr, bertrandjacques-m@orange.fr


Received December 2014

ABSTRACT
General relativity links gravitation to the structure of our space-time. Nowadays physics knows four types of interactions: Gravitation, electromagnetism, weak interactions, strong interactions. The theory of everything (ToE) is the unification of these four domains. We study several necessary cornerstones for such a theory: geometry and mathematics, adapted manifolds on the real domain, Clifford algebras over tangent spaces of these manifolds, the real Lagrangian density in connection with the standard model of quantum physics. The geometry of the standard model of quantum physics uses three Clifford algebras. The algebra 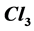 of the 3-dimensional physical space is sufficient to describe the wave of the electron. The algebra
of the 3-dimensional physical space is sufficient to describe the wave of the electron. The algebra 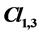 of space-time is sufficient to describe the wave of the pair electron-neutrino. A greater space-time with two additional dimensions of space generates the algebra
of space-time is sufficient to describe the wave of the pair electron-neutrino. A greater space-time with two additional dimensions of space generates the algebra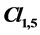 . It is sufficient to get the wave equation for all fermions, electron, its neutrino and quarks u and d of the first generation, and the wave equations for the two other generations. Values of these waves allow defining, in each point of space-time, geometric transformations from one intrinsic manifold of space-time into the usual manifold. The Lagrangian density is the scalar part of the wave equation.
. It is sufficient to get the wave equation for all fermions, electron, its neutrino and quarks u and d of the first generation, and the wave equations for the two other generations. Values of these waves allow defining, in each point of space-time, geometric transformations from one intrinsic manifold of space-time into the usual manifold. The Lagrangian density is the scalar part of the wave equation.
Keywords:
Geometry, Invariance Group, Dirac Equation, Electromagnetism, Weak Interactions, Strong Interactions, Clifford Algebras

Introduction
Geometry is equivalent to physics since Einstein has linked gravitation to the geometry of our Universe [1] [2]. The mathematical frame of this geometry is a 4-dimensional manifold where the dimension is this number of real parameters. Nowadays everyone in physics tries to produce a ToE (theory of everything), a theory including gravitation, electromagnetism, weak and strong interactions. String theory, supersymmetry, superstring theory, M-theory, loop quantum gravity, are most famous recent tentatives. This means that the problem is very hard. The aim of this paper is the analysis of these difficulties, preparing new trails to construct such a theory. The basic idea is: perhaps the solution is not so difficult, perhaps we have not be seeking in the right direction. After his discovery of general relativity, Einstein made numerous attempts [3] to get a theory unifying electromagnetism and gravitation. In the same time quantum mechanics was quickly growing, a relativistic wave equation was given by Dirac for the electron. It was then necessary to account not only for gravitation and electromagnetism, but also for the spin 1/2 of the electron and for the quantum wave. Difficulties here begin with the terrible difference between mathematical tools: the 4-dimensional real manifold of the general relativity versus quantum states using hermitical linear spaces over the complex field. Electromagnetism and weak interactions have been partially unified in the Weinberg-Salam model of electro-weak interactions [4], then strong interactions have been described by chromodynamics [5] and both are the main parts of the synthesis known as standard model of quantum physics.
All preceding attempts have supposed that the starting point was necessarily the standard model of quantum physics. The philosophical background of this choice is the believing in the necessity of the theoretical construction made from quantum mechanics. This comes historically from the fact that the first wave equation, found by E. Schrödinger, was able to account not only for one particle, but for a lot of them. Unhappily this wave equation is not relativistic. Consequently it is also unable to account for the spin 1/2, a common property for all fundamental fermions of relativistic quantum physics.
Since 1912 general relativity has made tremendous progress. Solutions were found justifying the behavior of stars with a very strong gravitational field, emitting gravitational waves. Calculations perfectly account for the measurements. On the contrary even if the quantum field theory claims still more precise results, such as the calculation of the Lamb effect or the calculation of the anomalous magnetic moment of the electron, the calculation is difficult: it is a process of successive approximations with the necessity to cut off not a small error but an infinite part of the result: this is not mathematically correct. In fact there are two quantum theories, the first and the second quantification. The first quantification uses for the electron a wave that is a function of space and time with value into the complex field or into a complex vector space. Calculations are exact in the case of the hydrogen atom and results are very precise. The second quantification transforms this wave into something very different, a field of operators operating on something, an object with no mathematical definition. Therefore on the mathematical point of view the departure of the ToE must be the general relativity and neither the second quantification nor any theory using the second quantification.
On the physical point of view it is the same from time properties. Time in physics is not space: in space we can go in any direction, in time we go only from past to future and there is strictly no way to go backwards. Gravitation propagates with gravitational waves that are emitted by stars and the move of these stars is changing with time. All laws of quantum physics are obtained from Lagrangian densities that give the wave equations from a principle of stationarity. This principle was inherited from classical mechanics where the time is not oriented if we forget frictions. Since the true time is the oriented time of thermodynamics, not the time of classical mechanics, only general relativity, allowing the use of an oriented time, is able to be the starting point of the ToE. General relativity and standard model are both obtained from a principle of stationarity, this is certainly another cornerstone to build the ToE (private discussion with D. Girardot).
1. Clifford Algebra of the 3-Dimensional Space
Clifford algebras on the real field are a necessary tool because particles with spin 1/2 exist. We use here all notations of “New insights in the standard model of quantum physics in Clifford Algebra” [6]. Its first chapter study at an elementary level the three Clifford algebras used in the present work. The algebra 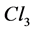 of the physical space is sufficient to describe the physical space-time because
of the physical space is sufficient to describe the physical space-time because
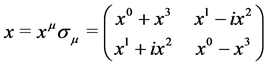 (1.1)
(1.1)
forms the auto-adjoint subspace of the Clifford algebra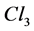 . The wave of an electron is a function of this part of
. The wave of an electron is a function of this part of 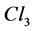 into the full algebra:
into the full algebra: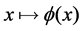 . The Dirac wave equation reads in this frame
. The Dirac wave equation reads in this frame
 (1.2)
(1.2)

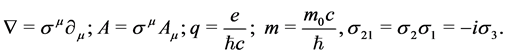 (1.3)
(1.3)
where 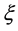 and
and 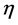 are respectively right and left Weyl spinors,
are respectively right and left Weyl spinors, 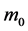 is the proper mass and
is the proper mass and 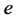 is the negative charge of the electron1. The Dirac equation is the linear approximation of our non-linear homogeneous wave equation
is the negative charge of the electron1. The Dirac equation is the linear approximation of our non-linear homogeneous wave equation
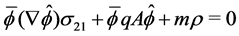 (1.4)
(1.4)
 (1.5)
(1.5)
where 
I recall now how the wave equation is said form invariant: If 





we note, if

We then get:





we get for








and non relativistic quantum mechanics uses the same relation with 

ticles with spin 
matrix representations of



Here (1.14) comes from (1.11) and (1.13). The relation (1.15) is necessary to get the gauge invariance of the electromagnetism and comes from

The relation (1.16) comes from (1.5), (1.7), (1.13) that give

and (1.16) is then equivalent to

The set 















Our wave equation is gauge invariant under two gauges. The first one is well known since it is the electric gauge

The second one is only a global gauge, it is the chiral gauge

Each gauge is linked to a conserved current. The current linked to the electric gauge is the current of probability

The second conserved current is the 

Components 







And the components 


There is no difference between the matrix product 




This means that the 


And since 









The geometric meaning of the Dirac wave is as follows: At each point of the space-time we have, not only one space-time manifold, but two space-time manifolds: the manifold of the 


2. Wave of Electron + Neutrino in Cl1,3
The electric gauge is the reason of the electric interaction of the electron. Similarly the second gauge of the electron is linked to the weak interaction of the electron. The Weinberg-Salam model of electro-weak interactions [4] considers the right 




Relativistic quantum mechanics supposes also a link between the wave of the particle and the wave of its anti-particle. Noting now 

Then the wave of electron + positron + neutrino + antineutrino is a function of 









The link between 



With this matrix representation the reverse of 

The invariant form of the wave equation of electron + neutrino reads [10]

where we have to define





The 





The 





and 


The invariant wave Equation (2.7) has a real scalar part [10] that is simply

where 

Then there is only one conservative current, it is the sum of the current of the electron and the same current for the neutrino. The wave equation is gauge invariant [10] under the 






which gives, with (1.19)

In the space-time algebra we use

We note 



Similarly to the electron case 



Relation (2.27) is equivalent to


Then D is an affine transformation where indices 1 and 2 play a very different role. This is evidently linked to the fact that 

We know three generations of leptons and quarks and the standard model study separately these three generations. The reason is simply that our physical space is three dimensional, and we get the wave equation of leptons three times. One of the three is (2.7) that reads:



To go from one generation to another one is simple: we permute indices 1, 2, 3 of 



We do not know if the muon is obtained by 







We must also change the link (2.1) between the wave of the particle and the wave of the antiparticle, link using a 

and we shall have a 3 index in the case of the last generation. We must also change the definition of left and right wave. For the second generation this becomes

and me must also permute the indexes in the geometric transformation (2.31). We can then understand why the Lagrangian density, which comes from the scalar part of the invariant equation, must be calculated separately for the pair electron-electronic neutrino and for the pair muon-muonic neutrino or tau-tauic neutrino.
If there are only three objects like


3. Standard Model in Cl1,5
The standard model adds to the leptons (electron and its neutrino) in the first “generation” two quarks 




The 







We use two projectors satisfying

Three operators act on quarks like on leptons:


The fourth operator acts differently on the lepton and on the quark sector:


These definitions are absolutely all that you have to change to go from the lepton case into the quark case, to get the gauge group of electro-weak interactions. We proved in [6] 6.3 that this gives:




This means that changing the coefficient 1 of 






which gives



Then all features of electro-weak interactions of leptons and quarks are simply obtained from the structure of the wave, itself linked to the structure of the space-time
The generators of the 

and eight operators









We explained in [9] how these operators are equivalent to the eight generators 




where the eight 

The gauge group is obtained by exponentiation. We use four numbers 



We get

in any order, because:


Therefore the set

is a 





The 


We then get the gauge group of the standard model, automatically, and not another group. It is impossible to get operators exchanging 









We have still supposed nothing on









and two similar equalities for colors g and b. Now we define two matrices 


and we got the remarkable identity [6]

Usually 


To add two quarks with three colors each in the second and in the third generation we need

and two similar definitions for colors g and b. Now since the 



The link between the reverse in 


This link does not exist in 



where we use the scalar densities 



We use



The wave Equation (3.48) is gauge invariant under the gauge transformation (3.37) to (3.41) [13]. It is form invariant under the transformation 

we get [13]

From (3.54) which is equivalent to

and from the link 

for any index








And since we can separate the different multivector parts, (3.60) is equivalent to the system:




With (1.7) (3.63) and (3.64) read


This separation between the different components of the global space-time explains why we usually see only the real components of the 4-dimensional space-time vector
The link (3.49) between the reversion into 




The transformation linked to the wave reads


Similarly to what we said from (1.26), 





Next we let




and we get

We consider now the geometric transformation





4. Concluding Remarks
A quantum wave equation generalizing the Dirac wave equation has been proposed to explain the experimental results of the standard model of quantum physics. It does not require the second quantification nor the very tedious calculations brought by its method of approximation. The wave is a true function of space and time with value into well-defined Clifford algebras. It will then be easier to bring together this frame and the solid similar frame of general relativity.
It is very important to notice that these two frames use a same time. This time is our oriented time and the invariance group of the wave conserves this orientation. When the variational calculus is used to go from a Lagrangian density to the corresponding wave equations an integration by parts is necessary, and the assumption that it is possible to cancel solutions at infinity. This hypothesis seems physically equivalent to suppress the propagation. The result is that quantum fields theory is fully satisfactory for stationary states but is structurally unable to account for any irreversible process. Our study explains why Lagrangian densities take place everywhere in quantum physics: they are only the scalar part of the invariant wave equations of fermions. They are not at all fundamental, they are only a mathematical tool.
Fermions are useful and fundamental, but our Universe has not only fermions but also boson waves. We suspect that the boson part of our universe, that contains the massless photon, does not come from a Lagrangian density. For instance the theory of the photon made by L. de Broglie [14] [15] gives not one, but two Lagrangian densities. This is normal since his photon comes from two Dirac waves, and each one brings its own Lagrangian density.
Another important point is emphasized by T. Socroun [16]: in order to get the unification between gravitation and electromagnetism, it is necessary to incorporate charges into potentials terms. This is equivalent, in fact, to the prescription made by Einstein itself that all laws of physics are covariant. With 







So the three charges disappear in the calculations. For electro-weak interactions and strong interactions we let

Then the covariant derivative (3.4) is simply

Why this has never been made? The reason is probably that theories of great unification consider the charges as slowly variable with the scale of energy and hope that when these charges become equal the structure of the gauge group is enlarged. This is strictly impossible when charges are integrated into potential terms. But this is a new scope as soon as we have linked the generators of the gauge group to the structure of the wave in (2.37) to (2.40), (3.10) to (3.13), (3.23) to (3.28). Since all attempts made to get the unification have failed, the incorporation of charges into potentials is a cornerstone for the ToE. To get the ToE perhaps will it be sufficient to link the Lagrangian density of the general relativity to the Lagrangian density coming from the standard model? (D. Girardot, private discussion) This density is the real scalar part of the invariant wave Equation (3.48)

This density is easily generalized to three generations of fundamental fermions:

It is indeed very sophisticated but on the mathematical point of view it is not so different from the Lagrangian density of general relativity, they are both real functions of space and time.
Another cornerstone of a future ToE is the fact that both theories use a covariant derivative. We must understand how these two covariant derivative coexists. A simple hypothesis coming from the double manifold encountered in (1.24) is that each one can be the covariant derivative on one of the two manifolds. Is one of these two manifolds simply embedded into the other?
Cite this paper
Claude Daviau,Jacques Bertrand, (2015) Geometry of the Standard Model of Quantum Physics. Journal of Applied Mathematics and Physics,03,46-61. doi: 10.4236/jamp.2015.31007
References
- 1. Einstein, A. (1912) Lichtgeschwindigkeit und Statik des Gravitationsfeldes. Annalen der Physik (ser. 4), 38, 355-369.
- 2. Einstein, A. (1912) Theorie des statischen gravitationsfeldes. Annalen der Physik (ser. 4), 38, 443-458.
- 3. Tonnelat, M.A. (1965) Les théories unitaires de l’électromagnétisme et de la gravitation. Gauthier-Villars, Paris.
- 4. Weinberg, S. (1967) A Model of Leptons. Phys. Rev. Lett., 19, 1264-1266. http://dx.doi.org/10.1103/PhysRevLett.19.1264
- 5. Matveev, V.A. and Tavkhelidze, A.N. (2006) The Quantum Number Color, Colored Quarks and QCD. In: RAS INR, Ed., 99th Session of the JINR Scientific Council, Dubna, Moscow.
- 6. Daviau, C. and Bertrand, J. (2014) New Insights in the Standard Model of Quantum Physics in Clifford Algebra. Je Publie, Pouillé-les-coteaux. http://hal.archives-ouvertes.fr/hal-00907848
- 7. Daviau, C. (2011) L’espace-temps Double. JePublie, Pouillé-les-coteaux.
- 8. Daviau, C. (2012) Double Space-Time and More. JePublie, Pouillé-les-coteaux.
- 9. Daviau, C. (2013) Invariant Quantum Wave Equations and Double Space-Time. Adv. in Im-aging and Electron Physics, 179, Chapter 1, 1-137.
- 10. Daviau, C. and Bertrand, J. (2014) Relativistic Gauge Invariant Wave Equation of the Electron-Neutrino. Journal of Modern Physics, 5, 1001-1022. http://dx.doi.org/10.4236/jmp.2014.511102
- 11. Daviau, C. and Bertrand, J. (2013) A Lepton Dirac Equation with Additional Mass Term and a Wave Equation for a Fourth Neutrino. Ann. Fond. Louis de Broglie, 38.
- 12. Daviau, C. (2012) Invariance of the Dirac Equation and of Electromagnetism. Adv. Appl. Clifford Algebras, 22, 611-623. http://dx.doi.org/10.1007/s00006-012-0351-7
- 13. Daviau, C. and Bertrand, J. (2014) A Wave Equation Including Leptons and Quarks for the Standard Model of Quantum Physics in Clifford Algebra. http://dx.doi.org/10.4236/jmp.2014.518210
- 14. de Broglie, L. (1940) La mécanique du photon, Une nouvelle théorie de la lumière: Tome 1 La lumière dans le vide. Hermann, Paris.
- 15. de Broglie, L. (1942) tome 2 Les interactions entre les photons et la matière. Hermann, Paris.
- 16. Socroun, T. (2014) Clifford to Unify General Relativity and Elec-tromagnetism. ICCA10, Tartu (Estonia), Submitted.
NOTES
1It seems that we are still using complex linear spaces. But actually anything in (1.2) is usual in classical physics: 







2Relativistic quantum mechanics enlarges the invariance under 
3The use for complex matrices here is also pure commodity. Matrix representations were used to get by induction on the dimension the main theorem of existence and unicity, up to an isomorphism, of all real Clifford algebras. All calculations may be done by using 




4As before me remark that we are always in a frame of classical physics on the real field. 























