Journal of Applied Mathematics and Physics
Vol.03 No.01(2015), Article ID:53571,6 pages
10.4236/jamp.2015.31002
Single Machine Scheduling with Time-Dependent Learning Effect and Non-Linear Past-Sequence-Dependent Setup Times
Yuling Yeh1, Chinyao Low2, Wen-Yi Lin2
1Department of Marketing and Logistics, Nan Kai University of Technology, Nantou, Chinese Taipei
2Institute of Industrial Engineering and Management, National Yunlin University of Science and Technology, Douliou, Chinese Taipei
Email: yip@nkut.edu.tw, lowcy@yuntech.edu.tw


Received October 2014

ABSTRACT
This paper studies a single machine scheduling problem with time-dependent learning and setup times. Time-dependent learning means that the actual processing time of a job is a function of the sum of the normal processing times of the jobs already scheduled. The setup time of a job is proportional to the length of the already processed jobs, that is, past-sequence-dependent (psd) setup time. We show that the addressed problem remains polynomially solvable for the objectives, i.e., minimization of the total completion time and minimization of the total weighted completion time. We also show that the smallest processing time (SPT) rule provides the optimum sequence for the addressed problem.
Keywords:
Scheduling, Time-Dependent Learning, Setup Time, Past-Sequence-Dependent, Total Completion Time

1. Introduction
In classical scheduling problems, it is reasonable and necessary to consider scheduling problems with setup times. In many realistic situations, the setup times are considered either sequence independent or sequence dependent. In the first case, the setup times are usually added to the job processing times while in the second case, the setup time for the job currently being scheduled depends on the previous one or ones already scheduled. Koulamas and Kyparisis [1] first introduced a scheduling problem with past-sequence-dependent setup times, i.e., the setup time is dependent on all already scheduled jobs. They showed that a standard single machine scheduling problem with psd setup times can be solvable in polynomial time when the objectives are the makespan, the total completion time and the total absolute differences in completion times, respectively. They also extended their results to nonlinear psd setup times.
Recently, there is a growing interest in the literature to study scheduling problems with a learning effect [1]-[9] [10]-[12], and some researches take setup times into the study problem as well, such as Kuo and Yang [13] considered a single machine scheduling with past-sequence-dependent setup times and job-independent learning effect and showed the problem remains polynomially solvable for the objectives of the makespan, the total completion time, the total absolute differences in completion times and the sum of earliness, tardiness and common due-date penalty. Wang [14] considered a single-machine scheduling problem with past-sequence-dependent setup times and time-dependent learning effect. He proved that the problem with minimization of some objectives, such as makespan, the total completion time and the sum of the quadratic job completion time can be solved in polynomial time, respectively. Wang [15] considered a single-machine scheduling problem with exponential time-dependent learning effect and past-sequence-dependent setup times. The author indicated that the smallest processing time (SPT) rule can provide an optimum schedule for some performance measures, such as makespan, the total completion time and the sum of the quadratic job completion time, respectively. Although applying learning concepts into the setup or processing operations have been extensively studied in scheduling literature, however, few of them take both considerations into account simultaneously. In this paper, we study a single machine scheduling problem with a learning effects model that includes the psd setup times and the actual processing time of a job as a function of the sum of the normal processing times of the jobs already scheduled. The optimal sequences are developed for the two objectives, minimization of the total completion time and the total weighted completion time.
2. Notations and Problem Description
In this section, addressing single machine scheduling problems, the actual processing time of a job is assumed to be a function of the sum of the normal processing times of the jobs already scheduled and the setup time of a job is proportional to the length of the jobs already processed. Let 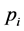 denote the normal processing time of job
denote the normal processing time of job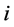 . In addition, let
. In addition, let 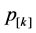 denote the normal processing time of a job if it is scheduled in the kth position in a sequence. For the proposed learning effect model, the actual processing time of a job j which is scheduled in the position r in a sequence,
denote the normal processing time of a job if it is scheduled in the kth position in a sequence. For the proposed learning effect model, the actual processing time of a job j which is scheduled in the position r in a sequence, 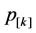 , is presented as
, is presented as
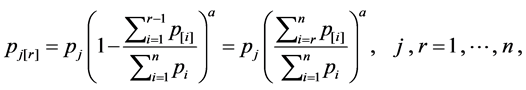 (1)
(1)
where 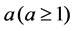 is learning effect indexes. Like Koulamas and Kyparisis [1], we assume that the non-linear past-sequence-dependent setup times of job
is learning effect indexes. Like Koulamas and Kyparisis [1], we assume that the non-linear past-sequence-dependent setup times of job 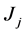 if it is scheduled in position
if it is scheduled in position 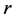 is given as follows:
is given as follows:
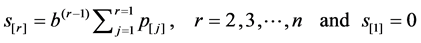 (2)
(2)
where 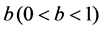 is a normalizing constant.
is a normalizing constant.
3. The Total Completion Time Criterion
Before you begin to format your paper, first write and save the content as a separate text file. Keep your text and graphic files separate until after the text has been formatted and styled. Do not use hard tabs, and limit use of hard returns to only one return at the end of a paragraph. Do not add any kind of pagination anywhere in the paper. Do not number text heads―the template will do that for you. In this section, we consider a single machine scheduling problem with the objective of minimizing the total completion time. We show that the problem
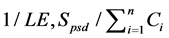 can be scheduled optimally by the SPT rule. Before proving Theorem 1, two lemmas are
can be scheduled optimally by the SPT rule. Before proving Theorem 1, two lemmas are
presented as follows.
Lemma 1. 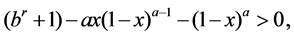 for
for 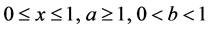 and
and 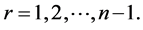
Proof. Let 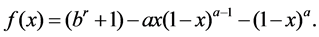 Then we have
Then we have 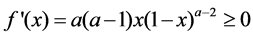 for
for 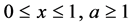 and
and
Hence, 




Lemma 2.

Proof. Let


Since 















Theorem 1. For the minimization of total completion time on a single machine scheduling problem

order of
Proof. For two adjacent jobs 


















tion time of the job 


the problem is minimized by sequencing the jobs in a SPT order, sufficient to show that (a) 

First, the proof of part (a) is given as follows.


we have

By substituting


From Lemma 2, we have


Note the proof of part (a) also shows that the makespan is minimized by the SPT rule. Furthermore, the proof of part (b) is given as follows.

and

we have
Since 

the fourth terms are non-negative as well. Therefore, this implies that
This completes the proof of (b) and thus of the theorem.
Hence, the optimal job-sequence of the single machine scheduling problem 

be solved in polynomial time.
4. The Total Weighted Completion Time Problem
For the problem to minimize the total weighted completion time, we show that an optimal solution if the processing times and the weights are agreeable, i.e., 



Lemma 3. 

Proof. Let 



Hence, 

Since 



Lemma 4.


Proof. Let


















Theorem 2. For minimization of the total weighted completion time on a single machine scheduling problem



and

Proof. Since


By substituting






From 



Hence,
Thus, the proof is completed.
Hence, the optimal job-sequence of the scheduling problem 

solved in polynomial time.
5. Conclusion
In this study, we analyzed a single machine scheduling problem with time-dependent learning and setup times. Time-dependent learning means that the actual processing time of a job is a function of the sum of the normal processing times of the jobs already scheduled. The setup time of a job is proportional to the length of the already processed jobs, that is, past-sequence-dependent (psd) setup time. The problem addressed with the two objectives, i.e., minimization of the total completion time and total weighted completion time, was studied in depth. We proved that the SPT rule can provide the optimal schedule for both the total completion time and total weighted completion time objectives. We also show that both the total completion time problem remains polynomially solvable, as does the total weighted completion time problem, under certain agreeable conditions.
Cite this paper
Yuling Yeh,Chinyao Low,Wen-Yi Lin, (2015) Single Machine Scheduling with Time-Dependent Learning Effect and Non-Linear Past-Sequence-Dependent Setup Times. Journal of Applied Mathematics and Physics,03,10-15. doi: 10.4236/jamp.2015.31002
References
- 1. Koulamas, C. and Kyparisis, G.J. (2008) Single-Machine Scheduling Problems with Past-Sequence-Dependent Setup Times. European Journal of Operational Research, 187, 1045-1049. http://dx.doi.org/10.1016/j.ejor.2006.03.066
- 2. Biskup, D. (1999) Single-Machine Scheduling with Learning Considerations. European Journal of Operations Research, 115, 173-178. http://dx.doi.org/10.1016/S0377-2217(98)00246-X
- 3. Biskup, D. and Herrmann, J. (2008) Single-Machine Scheduling against Due Dates with Past-Sequence-Dependent Setup Times. European Journal of Operational Research, 191, 587-592. http://dx.doi.org/10.1016/j.ejor.2007.08.028
- 4. Koulamas, C. and Kyparisis, G.J. (2007) Single-Machine and Two-Machine Flowshop Scheduling with General Learning Functions. European Journal of Operational Research, 178, 402-407. http://dx.doi.org/10.1016/j.ejor.2006.01.030
- 5. Mosheiov, G. (2001) Scheduling Problems with a Learning Effect. European Journal of Operational Research, 132, 687-693. http://dx.doi.org/10.1016/S0377-2217(00)00175-2
- 6. Mosheiov, G. and Sidney, J. (2003) Scheduling with General Job-Dependent Learning Curves. European Journal of Operational Research, 147, 665-670. http://dx.doi.org/10.1016/S0377-2217(02)00358-2
- 7. Kuo, W.H. and Yang, D.L. (2006) Minimizing the Total Completion Time in a Single-Machine Scheduling Problem with a Time-Dependent Learning Effect. European Journal of Operational Research, 174, 1184-1190. http://dx.doi.org/10.1016/j.ejor.2005.03.020
- 8. Kuo, W.H. and Yang, D.L. (2006) Minimizing the Makespan in a Single Machine Scheduling Problem with a Time- Based Learning Effect. Information Processing Letters, 27, 64-67. http://dx.doi.org/10.1016/j.ipl.2005.09.007
- 9. Kuo, W.H. and Yang, D.L. (2006) Single-Machine Group Scheduling with a Time-Dependent Learning Effect. Computers and Operations Research, 33, 2099-2112. http://dx.doi.org/10.1016/j.cor.2004.11.024
- 10. Lee, W.C. and Wu, C.C. (2004) Minimizing Total Completion Time in a Two-Machine Flowshop with a Learning Effect. International Journal of Production Economics, 88, 85-93. http://dx.doi.org/10.1016/S0925-5273(03)00179-8
- 11. Lee, W.C. and Wu, C.C. (2008) Single-Machine Scheduling Problems with a Learning Effect. Applied Mathematical Modelling, 32, 1191-1197. http://dx.doi.org/10.1016/j.apm.2007.03.001
- 12. Wang, J.B. (2008) Single-Machine Scheduling with General Learning Functions. Computers and Mathematics with Applications, 56, 1941-1947. http://dx.doi.org/10.1016/j.camwa.2008.04.019
- 13. Kuo, W.H. and Yang, D.L. (2007) Single Machine Scheduling with Past-Sequence-Dependent Setup Times and Learn- ing Effects. Information Processing Letters, 102, 22-26. http://dx.doi.org/10.1016/j.ipl.2006.11.002
- 14. Wang, J.B. (2008) Single Machine Scheduling with Past-Sequence-Dependent Setup Times and Time-Dependent Learning Effect. Computers and Industrial Engineering, 55, 584-591. http://dx.doi.org/10.1016/j.cie.2008.01.017
- 15. Wang, J.B. (2009) Single Machine Scheduling with Ex-ponential Time-Dependent Learning Effect Past-Sequence-Dependent Setup Times. Computers & Mathematics with Applications, 57, 9-16. http://dx.doi.org/10.1016/j.camwa.2008.09.025
















