J. Software Engineering & Applications, 2009, 2: 127-135
doi:10.4236/jsea.2009.22019 Published Online July 2009 (www.SciRP.org/journal/jsea)
A Performance-Driven Approach for Restructuring
Distributed Object-Oriented Software
Amal Abd El-Raouf1, Tahany Fergany2, Reda Ammar3, Safwat Hamad4
1Computer Science Department, Southern CT State University, New Haven, CT, USA; 2Computer Science Department, University of
New Haven, CT, New Haven, USA; 3Computer Science and Engineering Department, University of Connecticut, CT, Storrs, USA;
4Computer & Information Sciences Department, Ain Shams University, Abbassia, Cairo, Egypt.
Received March 1st, 2009; revised May 6th, 2009; accepted May 29th, 2009.
ABSTRACT
Object oriented techniques make applications substantially easier to build by providing a high-level platform for appli-
cation development. There have been a large number of projects based on the Distributed Object Oriented approach for
solving complex problems in various scientific fields. One important aspect of Distributed Object Oriented systems is
the efficient distribution of software classes among different processors. The initial design of the Distributed Object
Oriented application does not necessarily have the best class distribution and may require to be restructured. In this
paper, we propose a methodology for efficiently restructuring the Distributed Object Oriented software systems to get
better performance. We use Distributed Object-Oriented performance (DOOP) model as guidance for our restructuring
methodology. The proposed methodology consists of two phases. The first phase introduces a recursive graph clustering
technique to partition the OO system into subsystems with low coupling. The second phase is concerned with mapping
the generated partitions to the set of available machines in the target distributed architectur e.
Keywords: Performance Modeling, Distributed Object Oriented, Restructuring Methodolog y
1. Introduction
The software restructuring techniques present solutions
for the hardware/software mismatch problem in which
the software structure does not match the available
hardware organization [1,2,3,4]. There are two approa-
ches to solve such a problem; either to configure the
hardware to match the software components (hardware
reconfiguration), and/or to reconfigure the software
structure to match the available hardware by reorganiz-
ing its components (software restructuring). The first
approach is impractical especially in complex programs
containing many interacting modules (or subtasks). The
second approach is more practical especially in comput-
ing environments that contain large number of users. It
provides an optimal way to use the available system ca-
pabilities, reduces the overall computational cost, and
improves the overall system performance.
The basic idea of distributed software restructuring
techniques as described in [2] is to select the best alter-
native structure(s) for a constrained computing environ-
ment while reducing the overall resources need. These
structures can be created through; granularity definition
(merging of modules), alternative modules ordering, loop
decomposition, or multiple servers support. It has been
shown that performing software restructuring ahead of
the partitioning, allocation and scheduling phases im-
proved the results obtained from these phases and re-
duced the overall resources cost. Unfortunately this
technique is not applicable for Distributed Object Ori-
ented (DOO) systems.
In DOO systems, a program is organized as a set of
interacting objects, each of which has its own private
state rather than a set of functions that share a global
state. Classes represent abstraction that makes adapting
software easier and thus lower the cost of reuse, mainte-
nance and enhancement. OO paradigm is based on sev-
eral concepts such as encapsulation, inheritance, poly-
morphism, and dynamic binding [5,6]. Although these
features contribute to the reusability and extensibility of
systems, they produce complex dependencies among
classes. The most interesting feature of OO approach is
that objects may be distributed and executed either se-
quentially or in parallel [7]. Distributed objects are one
of the most popular programming paradigms in today’s
computing environments [8,9], naturally extending the

A Performance-Driven Approach for Restructuring Distributed Object-Oriented Software 128
sequential message-passing-oriented paradigm of ob-
jects.
Designing a distributed Object Oriented application
depends on how performance-critical the application is.
An important phase is to tune performance by “concre-
tizing” object locations and communication methods [10].
At this stage, it may be necessary to use tools to allow
analysis of the communication patterns among objects in
order to take the right allocation decision.
The principal goal of this research is to develop new
methodology for efficiently restructuring the DOO soft-
ware to fully exploit the system resources and get better
performance.
This paper is organized as follows: the second section
states the problem definition, including our objective and
assumptions. Section 3 describes the analytical DOOP
model its basic components and how it can be used to
measure the communication cost between different
classes. Section 4 presents the restructuring scheme and
the algorithm used in the first phase and the different
approaches proposed for the second phase of the re-
structuring process. Then a comparison and analysis of
generated results are included within Section 5. Finally,
Section 6 draws our conclusions.
2. Problem Definition
In this paper, we consider restructuring DOO applica-
tions for mapping on a distributed system that consists of
a collection of fully connected homogenous processors
in order to attain better performance. This process is
achieved in two phases illustrated in Figure 1. The first
phase is concerned with identifying clusters of a dense
community of classes within the DOO system. This
helps in decomposing the system into subsystems that
have low coupling and are suitable for distribution. The
inter-class communication is modeled as a class de-
pendency graph. In the second phase, we investigate the
possibilities of grouping the generated clusters and map-
ping them to the nodes of the distributed system. The
main objective is to propose a group of sub-systems,
each has maximum communication cost among the in-
ner-classes and the communication cost among the sub-
systems is minimized. Then, the proposed group of
sub-systems is mapped to the available nodes in the dis-
tributed system.
3. Distributed Object-Oriented Performance
Model
Performance analysis is a very important phase during
the software development process. It will ensure that the
system satisfies its performance objectives. Performance
analysis will not only evaluate the resources utilization
but also will allow comparing different design alterna-
tives, detecting bottlenecks, maintenance, re-use and
identify the tradeoffs.
Most OO approaches studying the performance of OO
systems are based on either the system measurements
after its development or mapping it to a conventional
performance model and hence no way to preserve the
OO features during the analysis phase.
In [11], the Distributed Object Oriented Performance
(DOOP) model was introduced. The DOOP model ana-
lyzes and evaluates the overall time cost considering the
Figure 1. Two-phase process for restructuring DOO software

A Performance-Driven Approach for Restructuring Distributed Object-Oriented Software 129
Figure 2. The DOOP model node structure
communication overheads while preserving the features,
properties and relationships between objects. According
to the model, each node in a DOO system will be repre-
sented as shown in Figure 2.
The performance model consists of two main parts:
the execution server and the communication server. The
execution server represents and evaluates the execution
cost of the software modules that reside on the target
node. The communication server provides the analysis of
the communication activities (including objects updating)
as well as the evaluation of the communication cost.
In our restructuring scheme, we utilize the DOOP
model in the evaluation process of the communication
activities among classes as shown below.
Assume that the overall arrival rate to the communica-
tion queue ck is given by:
ckcs cn cu

  (1)
where cs, cn and cu represent the communication arri-
val due to External User Request (EUR), Remote Re-
quest (RR), and updating objects’ data on other nodes,
respectively.
1
,,
N
css scnn ncuUi
i

 



where, βs and βn are the message multipliers for EUR and
RR. Let cui be the arrival rate corresponding to object i
data updating.
Since the updating process to an object i occurs due to
processing EUR or RR, Pi1 defined to be the probability
that object i is updated due to EUR, Pi2 is the probability
that object i is modified due to RR. cui can be expressed
as:
12cuii sin
PP




Hence, the expected communication service time for
each class will be:
s
nu
cs cnui
mm
ttt
RR

i
m
R
where tcs, tcn and tui are the expected communication ser-
vice time for EUR, RR and for update requests from ob-
ject i. While ms, mn and mui are the expected message
sizes of EUR, RR and of sending object i updating data.
R is the communication channel capacity. Furthermore,
the average communication service time for node (k) will
be:
λ
cs
λ cn
λ c
u
λs
λn
1
N
ckcs cscn cnui ui
i
tPtPt Pt


 (2)
λr
ck
cs
cs
p



ck
cn
cn
p



ck
ui
ui
p



where Pcs, and Pcn are the probabilities of activating
communication service by the external user requests and
by remote request respectively. Pui is the probability of
sending object i’s data update to other nodes.
4. Restructuring Scheme
Our restructuring scheme starts with using the DOOP
model to map the distribute Object Oriented application
into a Class Dependency Graph (CDG) illustrated in the
following subsection. Then this CDG is restructured us-
ing our two-phase methodology. The first phase is based
on a recursive use of a spectral graph bi-partitioning al-
gorithm to identify dense communities of classes. The
second phase is concerned with mapping the generated
partitions to the set of available machines in the target
distributed architecture. We will describe two proposed
approaches: the Cluster Grouping Approach and the
proposed Double K-Clustering Approach. The details of
each phase are described in the following subsections.
4.1 The Class Dependency Graph (CDG)
If we assumed that each individual class is initially allo-
cated to a separate node in the distributed system, then
the above DOOP model can be used as a powerful analy-

A Performance-Driven Approach for Restructuring Distributed Object-Oriented Software 130
Figure 3. A graph dependency graph for interclass communication
ALGORITHM GraphCluster(C, Clusters, CIndx)
INPUT: C = Adjacency matrix (weights matrix).
Clusters = a vector indicating the cluster no.
of each node in the CDG graph.
CIndx = the cluster index representing the
subgraph needed to be bi-partitioned.
OUTPUT: NewClus = a vector indicating which node in
the graph belongs to.
(1) Let CurrC be the extracted Adjacency matrix of the graph
indicated by CIndex.
(2) Partition the CurrC into two subgraphs
Indx =GraphBipart(CurrC)
(3) Create vector G1 and G2 to hold the indices of the first and
the second subgraphs respectively.
(4)
IF ( NOT WellPartitioned(CurrC, G1) ) OR
( NOT WellPartitioned(CurrC, G2) ) THEN
return Clusters
END IF
(5) Update NewClus with new portioning in G1 & G2.
(6)
Recursively bipartition the produced subgraphs G1 and G2
NewClus=GraphCluster(C, NewClus, CIndx*10+1)
NewClus =GraphCluster(C, NewClus, CIndx*10+2)
Figure 4. A recursive graph clustering algorithm
tical tool to accurately evaluate the communication ac-
tivities among classes in a distributed OO system. The
calculated values will be used to generate the Class De-
pendency Graph (CDG) of the given OO application.
The class dependency graph CDG as shown in Figure 3
is a graph representation for interclass communications.
In CDG, each class is represented as a vertex and an
edge between class A and B represents a communication
activity that exists between these two classes due to ei-
ther data transfer or classes’ dependency. The weight of
the edge WAB represents the cost of that communication
activity between class (A) and class (B). If no data
communication or relationship dependency has been
recognized between two classes, no edge will connect
them in the CDG.
4.2 First Phase: Clustering System Classes
In this section, we describe a clustering technique that is
considered the first primary phase of the restructuring
approach to be proposed in this paper. After applying
this step, the object oriented system is decomposed into
subsystems that have low coupling and are suitable for
distribution. The technique is based on a recursive use of
a spectral graph bi-partitioning algorithm to identify
dense communities of classes. At each recursive call, the
CDG is partitioned into two sub graphs each of which
will be further bi-partitioned as long as the partitioning
results in clusters that are denser than their parents.
Hence, the stopping condition depends on how good the
produced partition is. A sub-graph is considered a Well-
Partitioned if the summation of the weight of internal
edges (those between the vertices within a sub-graph)
exceeds those of external edges (those between the ver-
tices of the sub-graph and all the other vertices in other
sub-graphs). The iteration stops when at least one of the
produced sub-graphs is badly partitioned (the summation
of the weight of external edges exceeds those of internal
edges). In this case, the bi-partitioning step is considered

A Performance-Driven Approach for Restructuring Distributed Object-Oriented Software 131
obsolete and the algorithm will backtrack to the clusters
generated in the previous step. At the end, the identified
sub-graphs are the suggested clusters of the system. Fig-
ure 4 shows a detailed step by step description of the
clustering Algorithm as described in [12].
The mathematical derivation of the spectral factoriza-
tion algorithm used in our clustering approach was in-
troduced in [13]. It is originally solving the l-bounded
Graph Partitioning (l-GP) problem. However, we have
adapted the solution methodology to fit within our
bi-partitioning approach.
4.3 Second Phase: Mapping Classes to Nodes
In this phase, the restructuring process is accomplished
by mapping the set of DOO application clusters, resulted
from the first phase to the different network nodes in
order to attain better performance. To achieve this goal,
we perform the mapping process taking into considera-
tion our objective of minimizing the effect of class de-
pendency and data communication. It is assumed that the
target distributed system consists of a set of homogene-
ous processors that are fully connected via a communi-
cation network.
The mapping process has two cases. The first case
appears when the number of candidate clusters are less
than or equal to the number of the available nodes. In
this case the mapping process will be done simply by
assigning each cluster to one of the available nodes. The
problem occurs in the second case, when the number of
the generated clusters exceeds the number of available
nodes. This is a more realistic view since there will be
always huge software systems with large number of
classes and limited hardware resources.
In the following subsections, we are going to intro-
duce two different approaches to be used in performing
the grouping and mapping steps of the second phase:
the Cluster Grouping Approach and the Double
K-Clustering Approach. In Section 5, the results would
be compared with the direct K-Partitioning Approach
listed in Figure 4, where the graph is partitioned into a
pre-specified number equals exactly to the number of
nodes in the target distributed system. This is a one step
allocation process that also maintains the criterion of
minimizing inter-cluster communication cost.
4.3.1 The Cluster Grouping Approach:
In this approach, we use the clusters (sub-systems) gen-
erated at the first phase as the main candidates for dis-
tribution. The technique is based on merging clusters
into groups in a way that keeps the communication costs
among them minimized. As a result a cluster graph is
formed, where the nodes represent clusters and the edges
will capture the possible communication links that may
exist among clusters. Then, the K-Partitioning algorithm
is used to perform cluster grouping such that the number
of the resultant groups is equal to the number of avail-
able nodes. The result will be groups of clusters that
have minimal communication costs among them. Finally,
those groups are assigned to the different available nodes
in the distributed environment.
4.3.2 The Double K-Clustering Approach:
The K-Partitioning algorithm can not predict the number
of system modules or clusters as the recursive
Bi-Partitioning algorithm does. Instead, the number of
required clusters must be given as an input parameter
which is the k value. Hence, we will make use of the
advantages provided by both algorithms: the recursive
Bi-Partitioning and the K-Partitioning. So, the first phase
described in Section 3 is considered as a pre-phase to
estimate the number of the existing sub-systems within
the distributed application. However, we will use the
K-Partitioning algorithm twice. In the first time, the
original class dependency graph CDG is clustered ac-
cording to the number suggested at the pre-phase. In the
second time the K-Partitioning algorithm is used again in
the same way as in the cluster grouping approach illus-
trated above such that the number of the resultant groups
is equal to the number of available nodes. Then, the re-
sultant clusters are mapped to the available nodes.
5. Simulation and Results
In the section, we provide an analysis of both the clus-
tering and the mapping phases described above. This
illustration is done through a case study which describes
the detailed steps of the two-phase restructuring process
and a set of simulation experiments that were performed
to validate our results.
5.1 Case Study
We have developed a performance-driven restructuring
simulator using Matlab 7.0.4. A Graphical User Interface
(GUI) utility has been implemented to show the system
status after each step while the algorithm proceeds. The
simulator has a friendly user interface that allows the
user to specify the nodes and edges in the systems, and
then it will be able to generate the class dependency
graph (CDG).
We conducted an experiment using an OO system that
consists of 28 classes. The CDG that was generated by
the simulator for this system is given in Figure 5. In this
section we provide a step-by-step description of applying
the proposed restructuring techniques illustrated above.
Furthermore, we are going to analyze and compare the
results in each case. Figure 6 shows the resultant system
clusters generated by the proposed bi-partitioning algo-
rithm after the first phase. We can see that the proposed
first phase algorithm has created 7 clusters each of which

A Performance-Driven Approach for Restructuring Distributed Object-Oriented Software 132
Figure 5. The generated CDG
Figure 6. The resultant clusters generated by the restructuring
scheme first phase
Figure 7. Mapping the DOO system to a 4-node environment
using the direct partitioning approach
is marked up with a different color and surrounded by an
oval for further highlight.
Now, let us assume that the target distributed envi-
ronment consists of 4 homogenous nodes that are fully
connected. We need to apply any one of the second
phase approaches to map the classes to the distributed
nodes. First we applied the direct approach that parti-
tioned the original CDG into 4 clusters using the
k-partitioning algorithm. The resultant clusters are de-
picted in Figure 7. In Figure 8 the Cluster Grouping ap-
proach is applied to merge the clusters in Figure 8 gener-
ating 4 large clusters. However, applying the Double-K
clustering approach results in a completely different
group of clusters as shown in Figure 9. It started with
generating 7 clusters then they were grouped into 4 clus-
ters. The first one includes {C1, C2, C3, C4, C5, C6, C7,
C8}, the second one {C9, C10, C11, C12, C13, C14, C15,
C16, C17, C18, C19, C20, C22, C25, C26, C28}, the
third {C21, C23, C24}, and the last one includes only
C27.
Notice that each one of the approaches resulted in a
different grouping option, each of which has a different
communication cost. The Direct Partitioning Approach
results in a communication cost equals to 267 time unit.
While the Cluster Grouping resulted in a cost of 265 time
units, the Double-K produced a grouping of cost 223
time units.
Figure 8. Mapping the DOO system to a 4-node environment
using the cluster grouping approach
Figure 9. Mapping the DOO system to a 4-node environment
using the double-K approach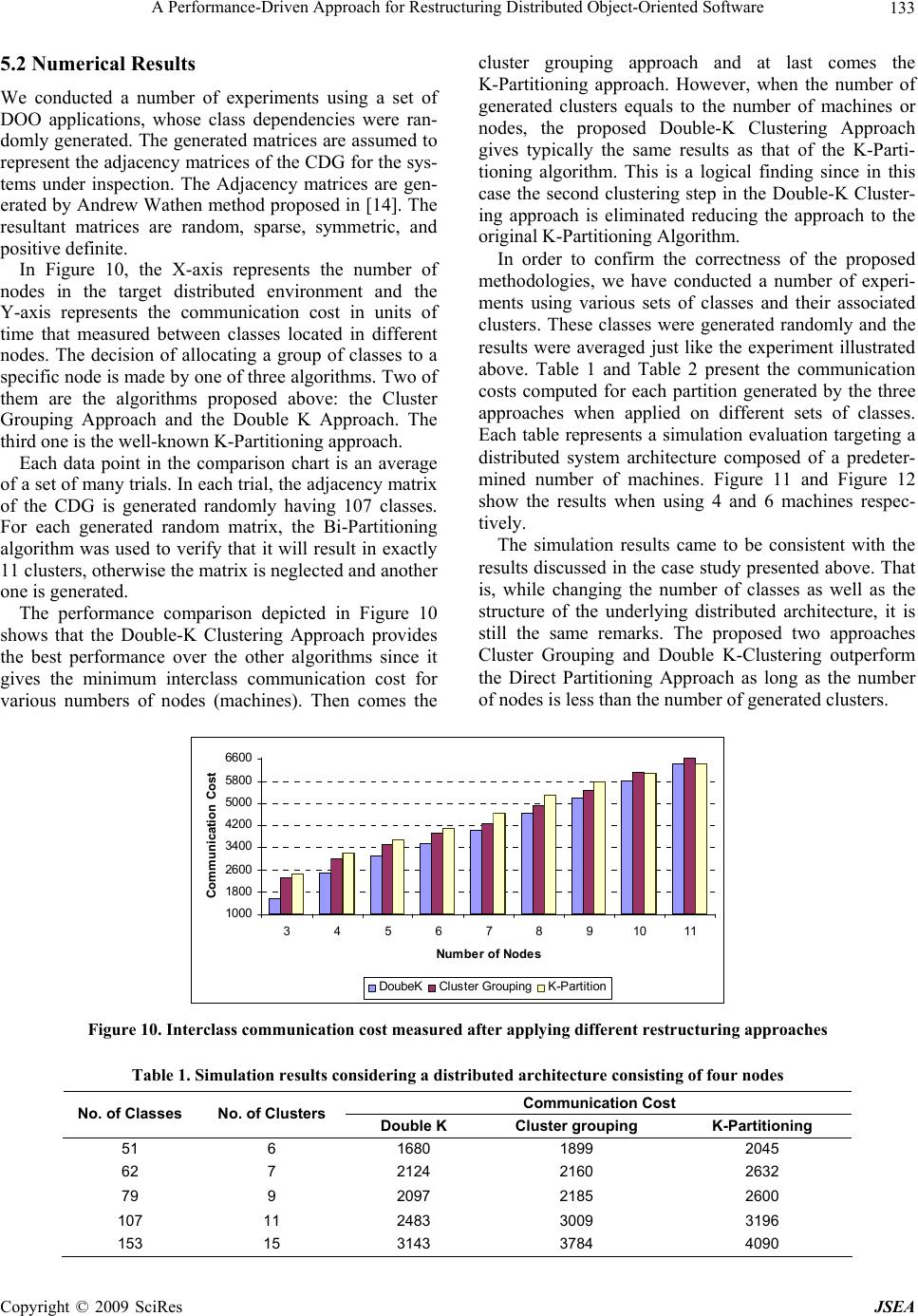

A Performance-Driven Approach for Restructuring Distributed Object-Oriented Software 133
5.2 Numerical Results
We conducted a number of experiments using a set of
DOO applications, whose class dependencies were ran-
domly generated. The generated matrices are assumed to
represent the adjacency matrices of the CDG for the sys-
tems under inspection. The Adjacency matrices are gen-
erated by Andrew Wathen method proposed in [14]. The
resultant matrices are random, sparse, symmetric, and
positive definite.
In Figure 10, the X-axis represents the number of
nodes in the target distributed environment and the
Y-axis represents the communication cost in units of
time that measured between classes located in different
nodes. The decision of allocating a group of classes to a
specific node is made by one of three algorithms. Two of
them are the algorithms proposed above: the Cluster
Grouping Approach and the Double K Approach. The
third one is the well-known K-Partitioning approach.
Each data point in the comparison chart is an average
of a set of many trials. In each trial, the adjacency matrix
of the CDG is generated randomly having 107 classes.
For each generated random matrix, the Bi-Partitioning
algorithm was used to verify that it will result in exactly
11 clusters, otherwise the matrix is neglected and another
one is generated.
The performance comparison depicted in Figure 10
shows that the Double-K Clustering Approach provides
the best performance over the other algorithms since it
gives the minimum interclass communication cost for
various numbers of nodes (machines). Then comes the
cluster grouping approach and at last comes the
K-Partitioning approach. However, when the number of
generated clusters equals to the number of machines or
nodes, the proposed Double-K Clustering Approach
gives typically the same results as that of the K-Parti-
tioning algorithm. This is a logical finding since in this
case the second clustering step in the Double-K Cluster-
ing approach is eliminated reducing the approach to the
original K-Partitioning Algorithm.
In order to confirm the correctness of the proposed
methodologies, we have conducted a number of experi-
ments using various sets of classes and their associated
clusters. These classes were generated randomly and the
results were averaged just like the experiment illustrated
above. Table 1 and Table 2 present the communication
costs computed for each partition generated by the three
approaches when applied on different sets of classes.
Each table represents a simulation evaluation targeting a
distributed system architecture composed of a predeter-
mined number of machines. Figure 11 and Figure 12
show the results when using 4 and 6 machines respec-
tively.
The simulation results came to be consistent with the
results discussed in the case study presented above. That
is, while changing the number of classes as well as the
structure of the underlying distributed architecture, it is
still the same remarks. The proposed two approaches
Cluster Grouping and Double K-Clustering outperform
the Direct Partitioning Approach as long as the number
of nodes is less than the number of generated clusters.
1000
1800
2600
3400
4200
5000
5800
6600
34567891011
Number of Node s
Communi cation Cost
DoubeK Cluster GroupingK-Partition
Figure 10. Interclass communication cost measured after applying different restructuring approaches
Table 1. Simulation results considering a distributed architecture consisting of four nodes
Communication Cost
No. of Classes No. of Clusters Double K Cluster grouping K-Partitioning
51 6 1680 1899 2045
62 7 2124 2160 2632
79 9 2097 2185 2600
107 11 2483 3009 3196
153 15 3143 3784 4090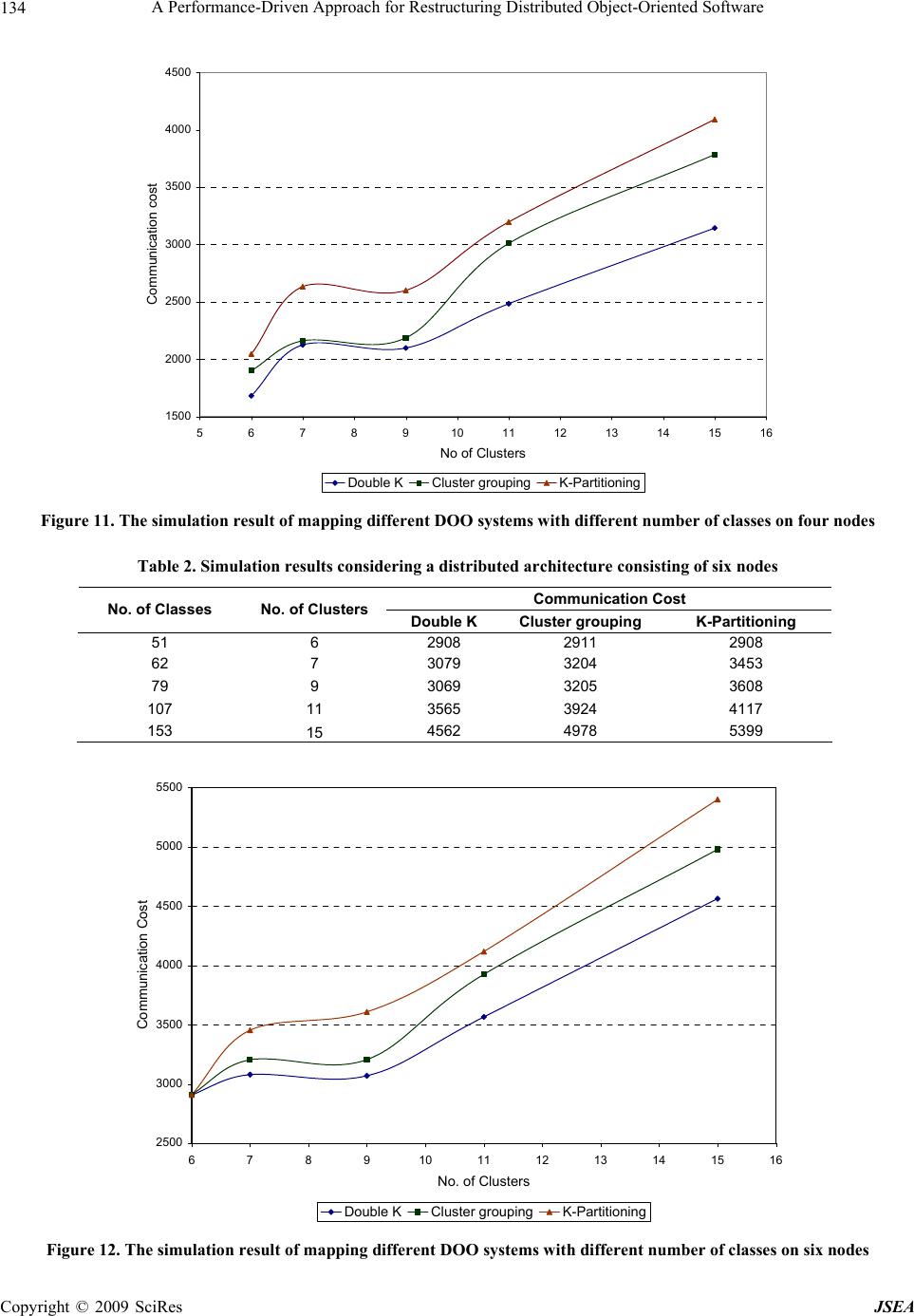

A Performance-Driven Approach for Restructuring Distributed Object-Oriented Software 134
1500
2000
2500
3000
3500
4000
4500
567891011121314151
No of Clusters
Communication cost
6
Double KCluster groupingK-Partitioning
Figure 11. The simulation result of mapping different DOO systems with different number of classes on four nodes
Table 2. Simulation results considering a distributed architecture consisting of six nodes
Communication Cost
No. of Classes No. of Clusters Double K Cluster grouping K-Partitioning
51 6 2908 2911 2908
62 7 3079 3204 3453
79 9 3069 3205 3608
107 11 3565 3924 4117
153 15 4562 4978 5399
2500
3000
3500
4000
4500
5000
5500
678910 11 12 13 14 15 16
No. of Clusters
Communication Cost
Double KCluster groupingK-Partitioning
Figure 12. The simulation result of mapping different DOO systems with different number of classes on six nodes

A Performance-Driven Approach for Restructuring Distributed Object-Oriented Software 135
6. Conclusions
In this paper, we proposed a restructuring approach for
DOO applications into a distributed system consisting of
a collection of fully connected homogenous processors.
The restructuring process was performed in two phases:
the clustering phase and the mapping phase. The first
phase is based on the theory of spectral graph bi-parti-
tioning, where the Distributed Object Oriented perform-
ance model was used efficiently to evaluate the commu-
nication costs between different classes. In the second
phase, the identified subsystems were assigned to differ-
ent machines in the target distributed environment. This
is done through two proposed algorithms: cluster group-
ing approach and the Double-K Clustering approach. A
Comparison was made between the proposed approaches
and the k-partitioning algorithm. The results showed that
the Double-K Clustering Approach provides the best
performance in terms of minimizing the communication
cost among classes located on different nodes (ma-
chines).
REFERENCES
[1] A. Raouf, R. Ammar, and T. Fergany, “Object oriented
performance modeling and restructuring on a pipeline
architecture,” The Journal of Computational Methods in
Science and Engineering, JCMSE, IOS Press, Vol. 6, pp.
59-71, 2006.
[2] T. A. Fergany, “Software restructuring in performance
critical distributed real-time systems,” Ph. D. Thesis,
University of Connecticut, USA, 1991.
[3] T. A. Fergany, H. Sholl, and R. A. Ammar, “SRS: A tool
for software restructuring in real-time distributed envi-
ronment,” in the Proceedings of the 4th International
Conference on Parallel and Distributed Computing and
Systems, October 1991.
[4] H. Sholl and T. A. Fergany, “Performance-require-
ments-based loop restructuring for real-time distributed
systems,” in the Proceedings of the International Confer-
ence on Mini and Microcomputers, From Micro to Su-
percomputers, Florida, December 1988.
[5] B. Meyer, “Object-oriented software construction,” Pren-
tice-Hall International (UK), Ltd, 1988.
[6] Ostereich, “Developing software with UML: OO analysis
and design in practice,” Addison Wesley, June 2002.
[7] J. K. Lee and D. Gannon, “Object oriented parallel pro-
gramming experiments and results,” in the Proceedings of
Supercomputing 91, IEEE Computer Society Press, Los
Alamitos, Calif, pp. 273-282, 1991.
[8] Sun Microsystems Inc. Java home page, http://www.java-
soft.com.
[9] J. Waldo, G. Wyant, A. Wollrath, and S. Kendall, “A
note on distributed computing,” Sun Microsystems
Laboratories, Technical Report-94-29, November 1994.
[10] I. Sommerville, “Software Engineering,” 8th Edition,
Addison-Wesley Publishers Ltd, New York, 2007.
[11] A. A. El-Raouf, “Performance modeling and analysis of
object oriented software systems,” PhD Dissertation,
Department of Computer Science & Engineering, Uni-
versity of Connecticut, 2005.
[12] S. Hamad, R. Ammar, A. Raouf, and M. Khalifa, “A
performance-driven clustering approach to minimize
coupling in a DOO system,” the 20th International Con-
ference on Parallel and Distributed Computing Systems,
Las Vegas, Nevada, pp. 24-26, September 2007.
[13] J. P. Hespanha, “An efficient MATLAB algorithm for
graph partitioning,” Technical Report, Department of
Electrical & Computer Engineering, University of Cali-
fornia, USA, October 2004.
[14] A. J. Wathen, “Realistic eigenvalue bounds for the
galerkin mass matrix,” The Journal of Numerical Analy-
sis, Vol. 7, pp. 449-457, 1987.