Journal of Materials Science and Chemical Engineering
Vol.03 No.01(2015), Article ID:53368,8 pages
10.4236/msce.2015.31012
Modeling and Simulation of Mechanical Properties of Nano Particle Modified Polyamide 6
I. Yi, J. Wiedmaier, U. Weber, S. Schmauder
Institute for Materials Testing, Materials Science and Strength of Materials, University of Stuttgart, D-70569 Stuttgart, Germany
Email: jing.wiedmaier@imwf.uni-stuttgart.de


Received January 2015

ABSTRACT
This paper discusses the utilization of nano-sized fillers in Polyamide 6 to increase the fracture resistance of the composites, which are crucial for various engineering applications. The toughening of the composites is achieved by using dispersed nano-scaled rubber particles (Polyether block copolymer) as the inclusion in Polyamide 6 matrix. For a better understanding of the mechanical behavior of the composites, it is indispensable to use analytical and numerical models for evaluating the overall mechanical behavior and damage mechanism of the composite. In this work the toughening mechanism is studied through literature review and by analytical modeling. The mechanical behavior of the composites such as elastic plastic and damage properties are calculated numerically with 3D representative volume element (RVE) models. The numerical results are compared with previously obtained experiments. The influence of volume fraction and aspect ratio of inclusions on the macroscopic stress strain curve as well as the size effect of inclusions and also the failure properties of the composite are studied in detail.
Keywords:
PA 6 Nanocomposite, Dispersed Rubber Particles, Toughening Mechanism, FEM Modeling, Mechanical Property

1. Introduction
One of the most important engineering thermoplastics is polyamide (PA, Nylon) due to its superior material properties such as outstanding mechanical performance, fine performance-cost ratio and etc. They are generally used in the manufacturing of automotive parts (tire cords, housing, air ducts and engine-room components), carpet liners and upholstery and electrical insulators [1].
PA 6 is the widely used type of polyamides. It is made from the polymerization of caprolactam. Because of the glass transition temperature of PA 6 at around 53˚C, it has limitations for certain usages, which need high impact toughness at room temperature. The toughness of PA 6 can be modified by adding dispersed rubber particles (polyether block copolymers, PA 6) as inclusion in the matrix. Good dispersion of rubber particles in PA 6 is hard to achieve due to the polar characteristic of PA 6. Therefore, special treatments are required for obtaining fine composites. The numerical results obtained in this work are compared with the experimental results conducted by Geier et al. [2]. Ultramid® B40 (PA 6) from BASF is used. The detailed specifications about PA 6 are available in Geier. Geier et al. selected the PA 6-polyether block copolymer as impact modifier. PA 6 and PA 6?polyether block copolymer have high material affinity. Therefore, these can be blended through the melt compounding process. The detailed process of melt compounding of the composite of PA 6 and PA 6-polyether block copolymer are discussed in Geier et al.
In this work, the main focuses are the research of toughening mechanisms of polymer composites through theoretical approaches and the study of stress-strain behavior via numerical approaches. Polyamide 6 (PA 6), as matrix, and PA 6?polyether block copolymer, as inclusion, composites are considered, so that the results obtained can be compared with the available experimental results from Geier [3].
2. Theoretical Approach
Different toughening mechanisms such as mechanical damping hypothesis [4], micro crack theory by Merz et al. in 1956 [5], multiple crazing theory by Bucknall and Smith in 1965 [6], shear yielding theory by Newman and Strella [7] have been proposed to improve the toughness of polymer composites. Since the cavitation of particles plays an important role in the toughening of rubber filled plastics, a prediction of the cavity initiation is a matter of concern. In this section, the cavitation criteria are introduced. A model of particle cavitation is advanced by Lazzeri and Bucknall [8]. Two assumed preconditions are
the largest defects of inclusions are micro holes with nanometer-ordered dimensions
the releasing of stored volumetric energy should be big enough to widen the surface area of holes and to extend the surrounding layers of inclusions for the expansion of micro holes.
The energy of the cavitated particle U is given by
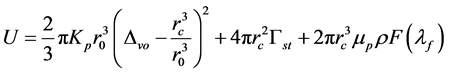
where Kp and μp are bulk and shear modulus of particle. The particle radius r0 and the cavity radius rc are included. ∆VO is the volume strain, and Γst is the surface tension of particle. The density ratio ρ and the function of the extension ratio of rubber at failure F(λF) are also involved. The first term of the right hand side represents the stored volumetric strain energy of the particle. The contributions from the surface energy (second term) and the shear strain energy (third term) are considered additionally. Lazzeri and Bucknall model contains 7 parameters (Kp, μp, rc, ∆VO, Γst, ρ, F(λF)). The 3 parameters (Kp, μp, Γst) are available normally. The others need to be measured from tests.
Fond and Schirrer [9] model uses a fracture mechanics approach. A volume criterion is included by the fact that decohesion does not occurr at the interface between the particle and the matrix. The cavitation appearing condition is defined by
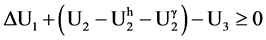
where U1 is the potential energy outside particles, and U2 is the elastic energy inside particles before the cavity appearance. U2h and U2γ are the elastic hydrostatic energy and the elastic shear energy in particles after the cavity appearance. The last term (U3) is the energy dissipated in the cavity formation. The formulas of each energy are given in Fond and Schirrer [9].
A simplified model is presented by approximations of the energy conservation. The minimum hydrostatic stress σh∞ for cavity initiation is derived as
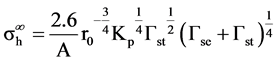
where
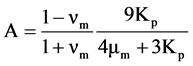
Matrix properties of vm and μm indicate Poisson’s ration and shear modulus. Kp is the homogenized bulk modulus of particle. The particle radius r0, the surface tension Γst and the surface energy Γse of particle are specified. These two equations require overall 5 parameters (vm, μm, Kp, Γst, Γse). Figure 1 illustrates the critical hydrostatic stress for cavitation (cavitation hydrostatic stress) of PA 6-N3000 composite as a function of particle radius. The surface tension of polyether is Γst = 0.050 J/m2 [10] and the surface energy is Γse = 0.050 J/m2 [9].
Note that for shear modulus μ

is used, and for the homogenized bulk modulus Kh
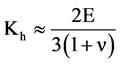
is used in Fond and Schirrer [9] instead of the well-known equation of bulk modulus
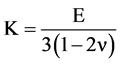
The concept of energy barrier is also introduced as a limitation of this model. Dependence between the critical hydrostatic stress and the particle radius is clearly observed and its curve (blue) in Figure 1. The cavitation hydrostatic stress decreases, as the rubber particle gets bigger. For example, it is predicted that the particle size of 10 nm PA 6-polyether block copolymer cavitates with the hydrostatic stress of 90 MPa and the 1 μm particle cavitates with 3 MPa. However, it is not realistic for relatively large sized particles (3 MPa would not create a cavity for the 1 μm particle). Thus the energy density ω is given by
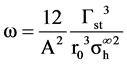
The red curve in Figure 1 represents this equation at r0 = 70 nm. It can be interpreted that the particle bigger than 70 nm requires the hydrostatic stress of 20 MPa. With energy barrier, the cavitation hydrostatic stress is independent of rubber size. For the employment of this concept, the energy density needs to be determined or measured from test. Here the energy density ω = 22650 J/m3 is assumed, and it give the cavitation stress of 20.00 MPa.
Application to the Composite of PA 6 and PA 6―Polyether Block Copolymer
In this paper, PA 6 and PA 6?polyether block copolymer (N3000) composites are selected, and the N3000 particles are regarded as perfect spheres. The cavitation mechanism for toughening behavior is considered because of soft featured inclusions (N3000). Geier et al. [3] observed the high affinity between PA 6 and N3000. Hence
Figure 1. Cavitation hydrostatic stress and energy barrier curve of PA 6-N3000 composite.
the cavitation will occur in the particles rather than the debonding of matrix and particles. The cavitation criterion of Fond and Schirrer is adopted for the numerical approach in Chapter 3. The particle, PA 6?polyether block copolymer (N3000), consists of PA 6 and 30 Mass-% (28.8 Vol.-%) of polyether. Assuming flawless synthesis processes and ideally dispersed polyether of N3000, the surface tension of polyether could be applicable to the entire part of N3000. Equator areas where the cavitation happens of N3000 particle is supposed to have the polyether Γst. Furthermore, these areas are realized as polyether areas in double sized particle for calculations of the cavitation hydrostatic stress of Fond and Schirrer.
3. Numerical Approach
3.1. Modeling
3.1.1. Geometry
The geometries of PA 6-N3000 composite are created using Digimat®-FE 5.0.1. Materials for the composite, PA 6 and N3000, are needed to be defined with Young’s modulus and Poisson’s ratio. The matrix of the composite is PA 6. The spherical inclusions, N3000, require a volume fraction and shape parameters. RVE size can be assigned with various setting options. All the N3000 particles are located in the matrix box. In other words, the particles are not cut by their matrix wall. The values of mechanical loading are also requisite parameters. Finally, RVE geometry can be generated and exported as *.step file. Two files (*.step and *_uncut.step) for matrix and one file for inclusion are created (Figure 2).
3.1.2. Meshing
Altair Hypermesh® 11 is employed for the meshing process. The *.step files are imported as a meshing geometry. The volume-tetramesh function of Altair Hypermesh® 11 is used for a cube-shaped RVE geometry. The mesh sizes should be assigned. In order to implement the periodic boundary condition, the entity sets of vertex nodes, edge nodes and surface nodes are defined. For further details regarding the meshing and the periodic boundary condition, refer Uhrig [11]. The input file for Abaqus® 6.12-1, *.inp, is created by Altair Hypermesh® 11. This input file includes nodes data, matrix and inclusion elements data and the entity sets (Figure 3).
Figure 2. RVE geometry of the volume fraction of 8.2 Vol.-%.
Figure 3. RVE mesh of the volume fraction of 8.2 Vol.-%.
3.1.3. Material Property
The used material properties, namely Young’s modulus, Poisson’s ratio and the plastic stress-strain values, of PA 6 and N3000 are to be found in [12].
3.2. Determination of RVE Size
3.2.1. Definition of RVE
The concept of RVE in homogenization describes relation between a macro-level and a meso-level. Some definitions of RVE are listed by Gitman [13]. Most of the definitions indicate two common points that are,
“RVE should contain enough information on the microstructure”, and
“RVE should be sufficiently smaller than the macroscopic structural dimensions” (Gitman [13]).
3.2.2. Procedure of RVE Size Determination
The procedure of RVE size determination proposed by Gitman [13].) is adopted.
1. The diameter of the inclusion is selected as 100nm, and the initial RVE size is chosen as 54.19 nm *54.19 nm (Since all of the RVE will have regular hexahedron shape, only the single edge length will be displayed in following, for example, 54.19 nm) for the first time.
2. The volume fraction of inclusion is fixed at 32.9 Vol.-%.
3. 5 models that have random geometries are created.
4. Abaqus® 6.12-1 calculations
5. Statistical analysis
6. The accuracy is selected in the range of 5% error of the average value of 5 models.
3.3. Extended Finite Element Method (XFEM)
FE models with an unmoving crack demand significant mesh refinements to match with discontinuous geometries. Moreover, a moving-crack FE model is more expensive because of successive mesh updates [14] and 2D planar models [15]. Belytschko and Black [16] proposed the concept of XFEM for the first time [14]. The term named by Daux et al. [17] as the extended finite element method [18]. XFEM is usually employed to model discontinuities (fracture analysis). The cavitation shows that a hole is created in the center of particles, and this hole grows. This phenomenon could be described by the onset and propagation of a crack. For this purpose, XFEM with the cohesive segments method is adopted to FE models.
Only the N3000 element set is assigned as a damage area (an enriched region). The command *ENRICHMENT with TYPE = PROPAGATION CRACK defines this damage area in Abaqus® 6.12?1 [14], and the default value of Geometric Properties is defined in the command *SURFACE INTERACTION. In order to initiate and propagate cracks from the middle of particles, the center elements of each N3000 particle are listed in a command *INITIAL CONDITIONS with TYPE = ENRICHMENT [14]. TYPE=ENRICHMENT needs two signed distance functions which are related to a crack surface and an orthogonal surface respectively. Small values close to zero (−0.01 and 0.01) are defined in the first signed distance function. This ensures that a crack will begin at the element boundaries. The second signed distance function is specified as −0.01. The command *ENRICHMENT with TYPE = PROPAGATION CRACK will continuously create cracks in elements which fulfill the damage criterion even after the complete cavitation (bisection) of particles. Those phenomena are more realistic and presumable. However, these cause calculation and iteration problems. Thus, the command *ENRICHMENT ACTIVATION with ACTIVATE = AUTO OFF is added in the step definition [14]. This command will stop the crack growth when all the pre-created cracks reach the boundary of particles.
For the damage parameters the command *DAMAGE INITIATION, *DAMAGE EVOLUTION and *DAMAGE STABILIZATION are included to N3000 material. MAXPS (maximum principal stress) and MAXPE (maximum principal strain) CRITERION options of the command *DAMAGE INITIATION are available for XFEM. In the command *DAMAGE EVOLUTION, either TYPE = DISPLACEMENT or TYPE = ENERGY option has to be chosen. The command *DAMAGE STABILIZATION could be used. Here, a viscosity coefficient is specified which will contribute to the calculation convergence.
Additionally, necessary output identifiers are added to the output request definition. PHILSM in the command *NODE OUTPUT and STATUSXFEM in the command *ELEMENT OUTPUT are put in for the proper post- processing.
3.4. Damage Parameters
From Section 2, the hydrostatic stresses that create cavitation are computed. Those values are assigned in the command *DAMAGE INITIATION with CRITERION = MAXPS. The stress values which depend on the particle diameter are enumerated in Table 1.
4. Results and Discussion
4.1. Comparison with Experiments
The models which contain all the design factors in Chapter 3 are calculated by the solver Abaqus 6.12-1. Three RVE models listed in Table 1 are simulated. Furthermore, these are compared with available uniaxial tensile test results (Figure 4).
4.2. Size Effect
The size effect of the particle is studied with the selected diameters of the N3000 (60, 100 and 140 nm). Figure 5 is the comparison of the simulation results of the volume fraction of 32.9 vol-%. Composite with larger particles is softer, because larger particles are easier to become caviated according to the calculation from Section 2.
Figure 4. Experiment and FE model curves, 8.2 Vol.-% (top), 16.5 Vol.-% (middle), 32.9 Vol.-% (bottom), particle size 100 nm.
Table 1. Particle size and hydrostatic stress.
Figure 5. Size effect (32.9 Vol.-%) stress-strain curve (Left) and magnified view (Right).
5. Conclusions
The toughness of polymer composites is improved by the addition of rubber particles. Understanding of particle toughening mechanism is important for the composite controlling.
Theoretical approach for toughening mechanisms is carried out in Section 2. Mechanical damping hypothesis, micro crack theory, multiple crazing theory and shear yielding theory are reviewed briefly as a history of toughening theory. Cavitation criteria are discussed. Lazzeri and Bucknall model is presented. Their model contains the stored volumetric strain energy, the surface energy and the shear strain energy. Fond and Schirrer defined the cavity condition. With their simplified model, the cavitation hydrostatic stress can be calculated. The energy barrier concept is also introduced. In Section 3, numerical approach is performed. First of all, the design procedure is decided. The determination of RVE size is studied. The proper RVE sizes are calculated by guidelines of Gitman. The cavitation phenomenon is introduced to finite element models with damage parameters (XFEM). RVEs with the various particles are decided for the study of particle size effect.
The FE simulation results are compared with the experimental results in Section 4. As the volume fraction of inclusion increases, the damage amount is also increased. The particle size effects are also notified. Composite with larger particles is softer than those with smaller particles.
Cite this paper
I. Yi,J. Wiedmaier,S. Schmauder, (2015) Modeling and Simulation of Mechanical Properties of Nano Particle Modified Polyamide 6. Journal of Materials Science and Chemical Engineering,03,80-87. doi: 10.4236/msce.2015.31012
References
- 1. Vaidya, U. (2011) Composites for Automotive, Truck and Mass Transit: Materials, Design, Manufacturing. Chapter 2 Polymer Resins, Additives and Sandwich Cores for Automotive, Mass Transit and Heavy Trucks. DEStech Publications, Inc., Lancaster.
- 2. Geier, S., Poindl, M. and Eyerer, P. (2010) Toughening of PA 6 by Fine Dispersed Nanosized PA 6-Polyether Block Copolymer Particles. Proceeding of the Polymer Processing Society, 26th Annual Meeting.
- 3. Geier, S. (2011) Optimierung von Steifigkeit/Z?higkeits-Eigenschaften Nanoskaliger Polyamid 6-Verbund-Werkstoffe Durch Analyse von Struktur/Eigenschafts-Korrelationen Stuttgart, Univ., Diss.
- 4. Bucknall, C.B. (1977) Toughened Plastics. Chapter 7 Mechanisms of Rubber Toughening. Applied Science Publ., Lon-don.
- 5. Merz, E.H., Claver, G.C. and Baer, M. (1956) Studies on Heterogeneous Polymeric Systems. Journal of Polymer Science, 22, 325-341. http://dx.doi.org/10.1002/pol.1956.1202210114
- 6. Bucknall, C.B. and Smith, R.R. (1965) Stress-Whitening in High-Impact Polystyrenes. Polymer, 6, 437-446. http://dx.doi.org/10.1016/0032-3861(65)90028-5
- 7. Newman, S. and Strella, S. (1965) Stress-Strain Behavior of Rubber-Reinforced Glassy Polymers. Journal of Applied Polymer Science, 9, 2297-2310. http://dx.doi.org/10.1002/app.1965.070090621
- 8. Lazzeri, A. and Bucknall, C.B. (1993) Dilatational Bands in Rubber-Toughened Polymers. Journal of Materials Science, 28, 6799-6808. http://dx.doi.org/10.1007/BF00356433
- 9. Fond, C. and Schirrer, R. (1996) A Mechanical Model for the Onset of Damage in Rubber Modified Amorphous Polymers. Journal de Physique IV, 6, C6-375-C6-384.
- 10. Grundke, K., Michel, S., Knispel, G. and Grundler, A. (2008) Wettability of Silicone and Polyether Impression Materials: Characterization by Surface Tension and Contact Angle Measurements. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 317, 598-609.
- 11. Uhrig, M. (2014) Numerische Simulation der mechanischen Eigenschaften nanopartikel gefüllter Polyamid 6-Composites via RVE Modellierung Stuttgart, Univ., Studienarbeit.
- 12. Huang, J., Schmauder, S., Weber, U. and Geier, S. (2011) Micromechanical Modelling of the Elastoplastic Behaviour of Nano-dispersed Elastomer Particle-Modified PA 6. Computational Materials Science, 52, 107-111.
- 13. Gitman, I.M. (2006) Representative Volumes and Multi-Scale Modelling of Quasi-Brittle Materials. Delft, Univ., Diss.
- 14. Abaqus 6.12: Analysis User’s Manual, Volume II: Analysis Dassault Systèmes, 2013.
- 15. Abaqus 6.12: Abaqus/CAE User’s Manual Dassault Systèmes, 2013.
- 16. Belytschko, T. and Black, T. (1999) Elastic Crack Growth in Finite Elements with Minimal Remeshing. International Journal for Numerical Methods in Engineering, 45, 601-620. http://dx.doi.org/10.1002/(SICI)1097-0207(19990620)45:5<601::AID-NME598>3.0.CO;2-S
- 17. Daux, C., Mo?s, N., Dolbow, J., Sukumar, N. and Belytschko, T. (2000) Arbitrary Branched and Intersecting Cracks with the Extended Finite Element Method. International Journal for Numerical Methods in Engineering, 48, 1741- 1760, http://dx.doi.org/10.1002/1097-0207(20000830)48:12<1741::AID-NME956>3.0.CO;2-L
- 18. Karihaloo, B.L. and Xiao, Q.Z. (2003) Modelling of Stationary and Growing Cracks in FE Framework without Remeshing: A State-of-the-Art Review. Computers & Structures, 81, 119-129. http://dx.doi.org/10.1016/S0045-7949(02)00431-5








